Параллелограмм

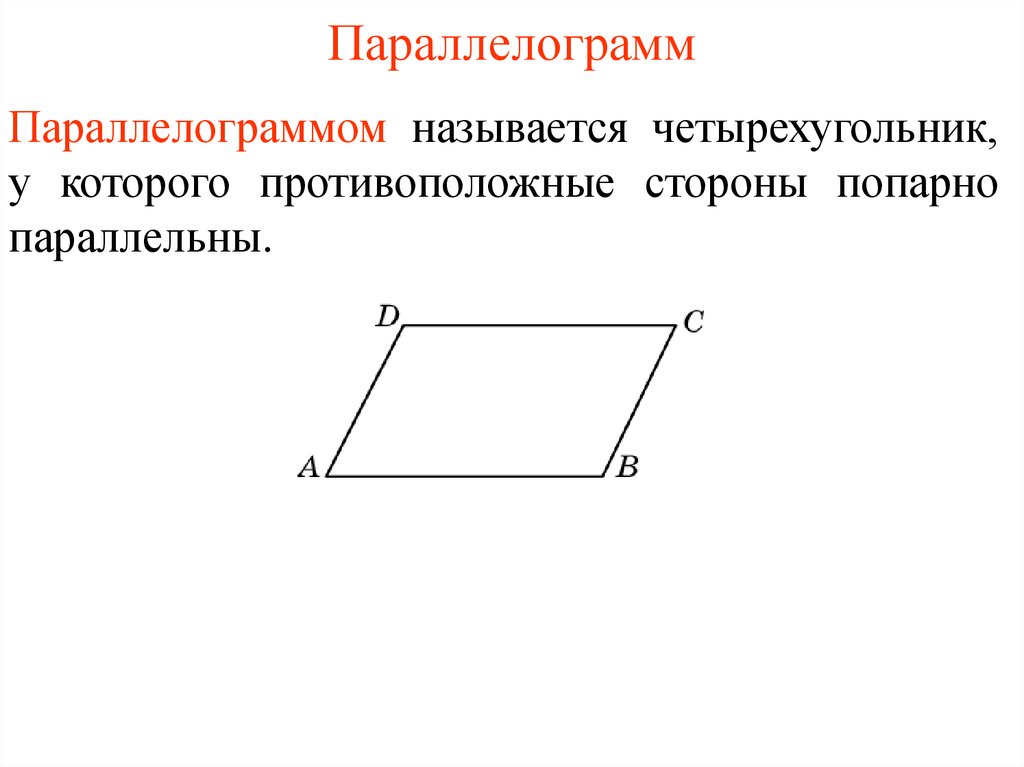
Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

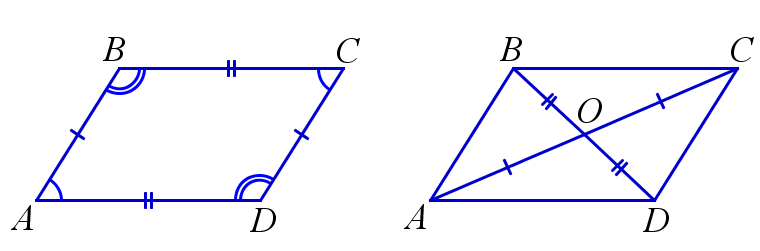
У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
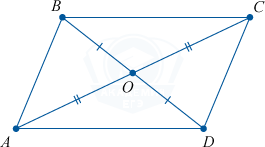
Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
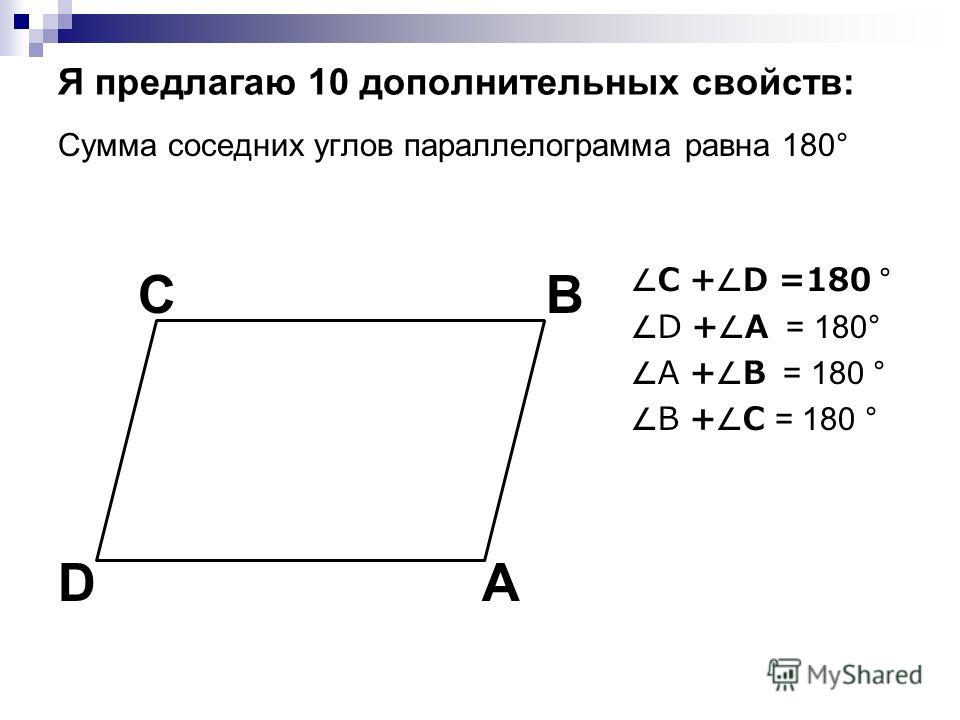
Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Признаки параллелограмма

У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для .

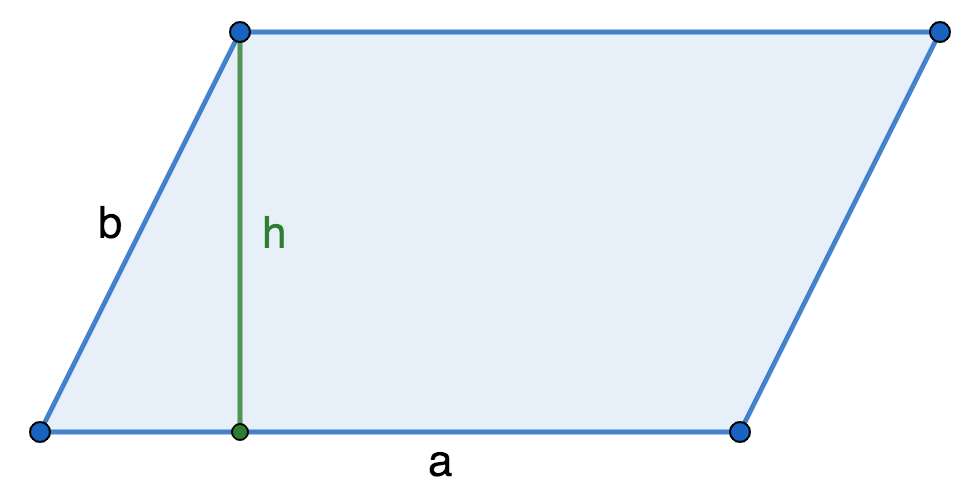
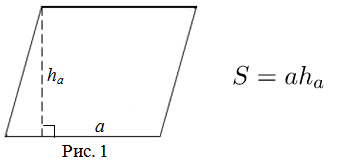
Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

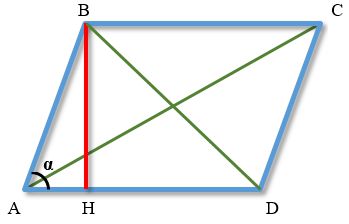
Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

Также площадь параллелограмма может быть выражена через стороны a, b{\displaystyle a,\ b} и длину любой из диагоналей d{\displaystyle d} по формуле Герона как сумма площадей двух равных примыкающих треугольников:

S=2⋅p(p−a)(p−b)(p−d){\displaystyle S=2\cdot {\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)2.{\displaystyle p=(a+b+d)/2.}

Как рассчитать площадь параллелограмма

С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.

Вычисление площади параллелограмма по высоте.
Вычисление площади параллелограмма по углам. Если известны длины сторон и хотя бы один угол, то можно применить следующую формулу.
Вычисление площади параллелограмма по диагоналям. Для этого надо знать не только длину диагоналей, но и величину угла между ними. И тогда можно применять следующую формулу.

Вот и все, что мы хотели рассказать о ПАРАЛЛЕЛОГРАММЕ. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для .

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

S=2p(p−a)(p−b)(p−d){\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)2.{\displaystyle p=(a+b+d)/2.}

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для .

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

S=2p(p−a)(p−b)(p−d){\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)2.{\displaystyle p=(a+b+d)/2.}

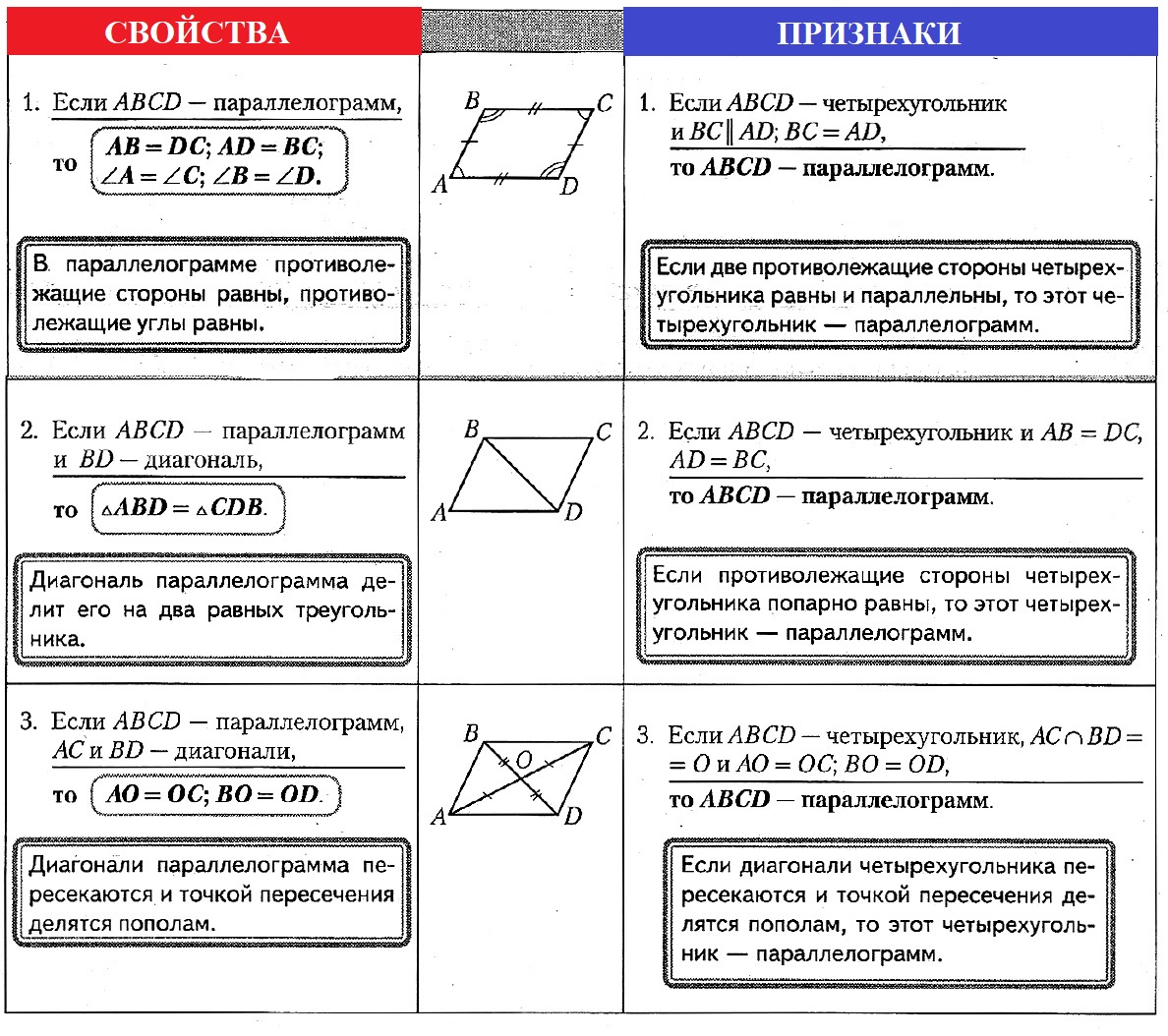
Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам.

Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

Противолежащие стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

|AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.
Точка пересечения диагоналей является центром симметрии параллелограмма.
Параллелограмм диагональю делится на два равных треугольника.
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырехугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.

Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам.

Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

Противолежащие стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

|AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.
Точка пересечения диагоналей является центром симметрии параллелограмма.
Параллелограмм диагональю делится на два равных треугольника.
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам.

Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

Противолежащие стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

|AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.
Точка пересечения диагоналей является центром симметрии параллелограмма.
Параллелограмм диагональю делится на два равных треугольника.
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Признаки параллелограмма

У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.

\( AB = CD \); \( AB || CD \Rightarrow ABCD \) — параллелограмм.

Рассмотрим подробнее. Почему \( AD || BC \)?

\( \triangle ABC = \triangle ADC \) по свойству 1: \( AB = CD \), \( \angle 1 = \angle 2 \) как накрест лежащие при параллельных \( AB \) и \( CD \) и секущей \( AC \).

Но если \( \triangle ABC = \triangle ADC \), то \( \angle 3 = \angle 4 \) (лежат напротив \( AD || BC \) (\( \angle 3 \) и \( \angle 4 \) — накрест лежащие тоже равны).

Первый признак верен.

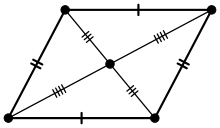
\( AB = CD \), \( AD = BC \Rightarrow ABCD \) — параллелограмм.

Рассмотрим данный признак. Еще раз проведем диагональ \( AC \).

По свойству 1 \( \triangle ABC = \triangle ACD \).

Из этого следует, что: \( \angle 1 = \angle 2 \Rightarrow AD || BC \) и \( \angle 3 = \angle 4 \Rightarrow AB || CD \), то есть \( ABCD \) — параллелограмм.

Второй признак верен.

3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны

\( \angle A = \angle C \), \( \angle B = \angle D \Rightarrow ABCD \) — параллелограмм.

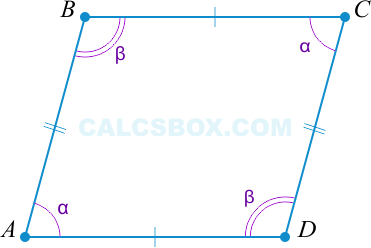
\( 2 \alpha + 2 \beta = 360^{\circ} \) (поскольку \( \angle A = \angle C \), \( \angle B = \angle D \) по условию).

Получается, \( \alpha + \beta = 180^{\circ} \). Но \( \alpha \) и \( \beta \) являются внутренними односторонними при секущей \( AB \).

И то, что \( \alpha + \beta = 180^{\circ} \) говорит и о том, что \( AD || BC \).

При этом \( \alpha \) и \( \beta \) — внутренние односторонние при секущей \( AB || CD \).

Третий признак верен.

Свойства и признаки параллелограмма

Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.

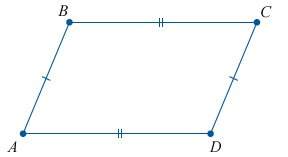
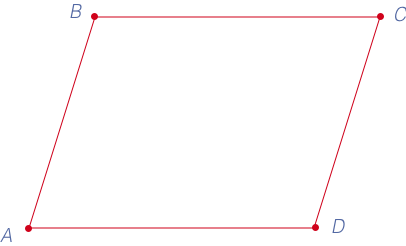
Возьмем в качестве примера еще раз нашу фигуру:

Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:

Две противоположные стороны попарно параллельны.
Две противоположные стороны попарно равны между собой.
Две противоположные стороны и равны, и параллельны. В данном случае можно брать только одну пару сторон.
Противоположные углы попарно равны между собой.
Диагонали пересекаются в центре фигуры и делятся точкой пересечения на две равные части.
Если сложить два соседних угла, то получится 180 градусов.

Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:

Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.

Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.

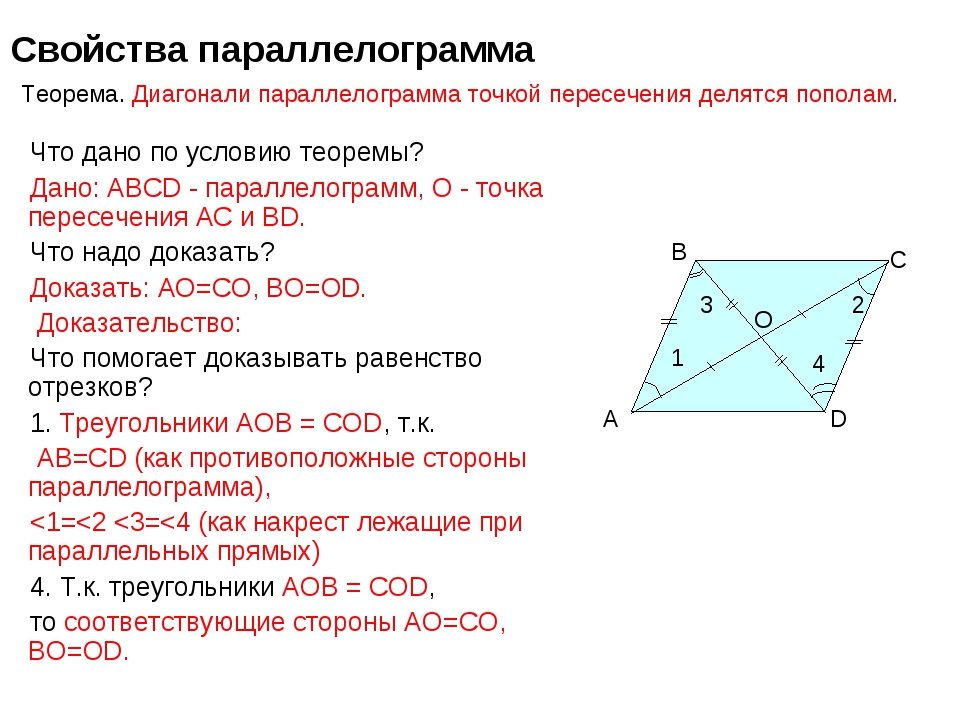
Свойства параллелограмма

1. Противоположные стороны тождественны

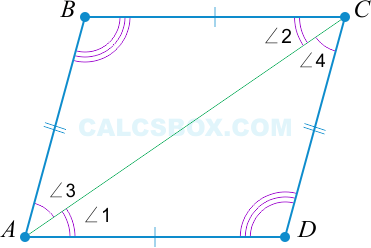
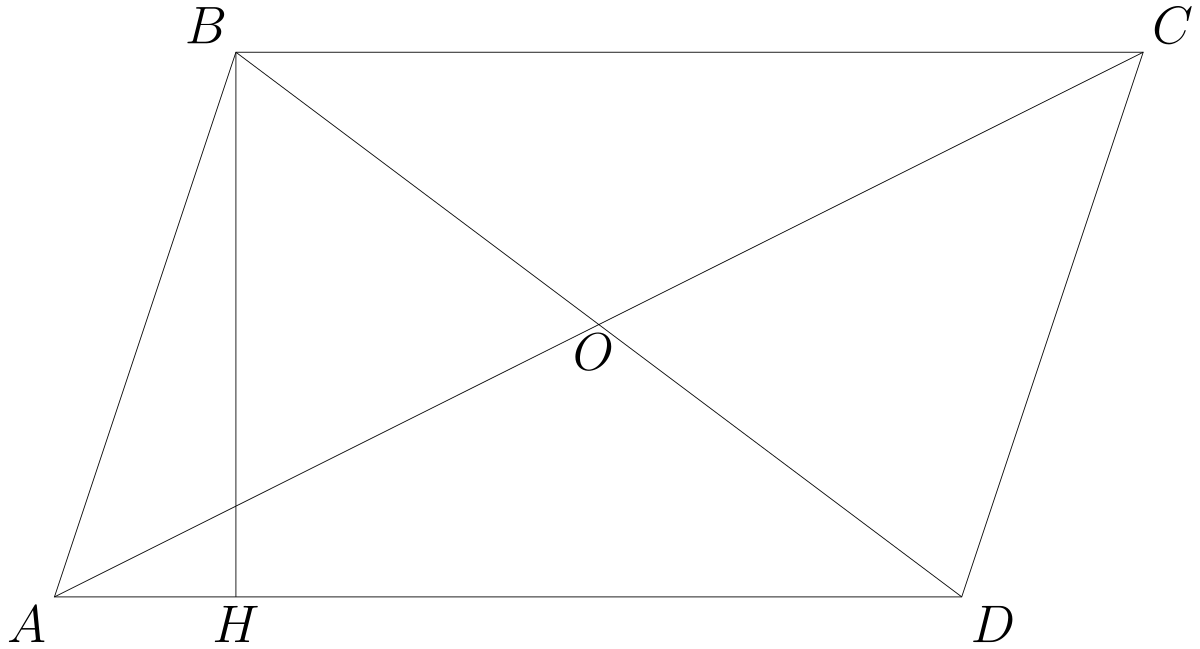
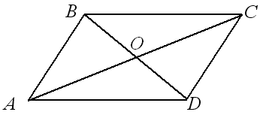
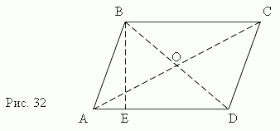
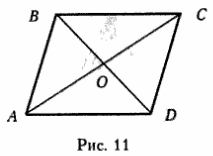
Первым делом проведем диагональ \( AC \). Получаются два треугольника: \( ABC \) и \( ADC \).

Так как \( ABCD \) — параллелограмм, то справедливо следующее:

\( AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.

\( AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.

Следовательно, \( \triangle ABC = \triangle ADC \) (по второму признаку: \( \angle 1 = \angle 2, \angle 3 = \angle 4 \) и \( AC \) — общая).

И, значит, \( \triangle ABC = \triangle ADC \), то \( AB = CD \) и \( AD = BC \).

2. Противоположные углы тождественны

Согласно доказательству свойства 1 мы знаем, что \( \angle 1 = \angle 2, \angle 3 = \angle 4 \). Таким образом сумма противоположных углов равна: \( \angle 1 + \angle 3 = \angle 2 + \angle 4 \). Учитывая, что \( \triangle ABC = \triangle ADC \) получаем \( \angle A = \angle C \), \( \angle B = \angle D \).

3. Диагонали разделены пополам точкой пересечения

По свойству 1 мы знаем, что противоположные стороны тождественны: \( AB = CD \). Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \( \triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \( BO = OD \) (напротив углов \( \angle 2 \) и \( \angle 1 \)) и \( AO = OC \) (напротив углов \( \angle 3 \) и \( \angle 4 \) соответственно).

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для .

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

S=2p(p−a)(p−b)(p−d){\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)2.{\displaystyle p=(a+b+d)/2.}

Происхождение термина «параллелограмм»

Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.

Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».

Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.

Признаки параллелограмма

У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Признаки параллелограмма

У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам.

Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

Противолежащие стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

|AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.
Точка пересечения диагоналей является центром симметрии параллелограмма.
Параллелограмм диагональю делится на два равных треугольника.
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для .

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

S=2p(p−a)(p−b)(p−d){\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)2.{\displaystyle p=(a+b+d)/2.}