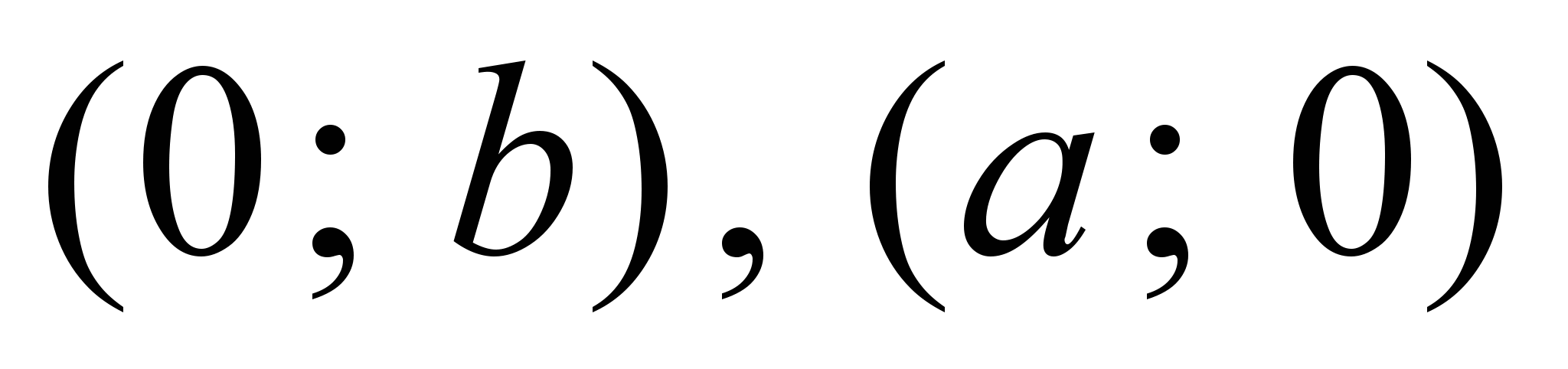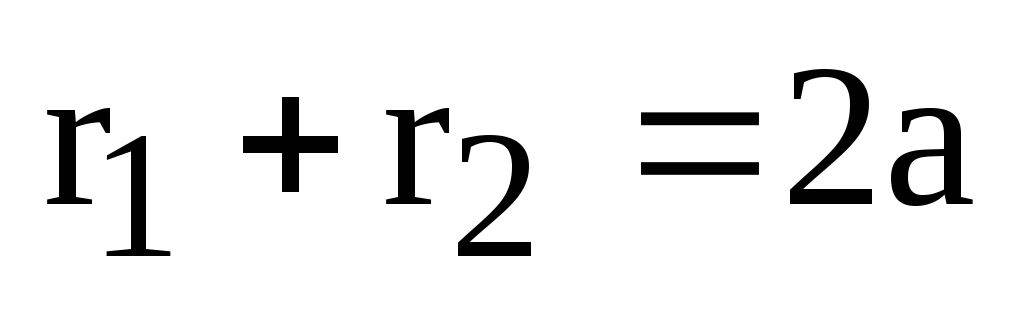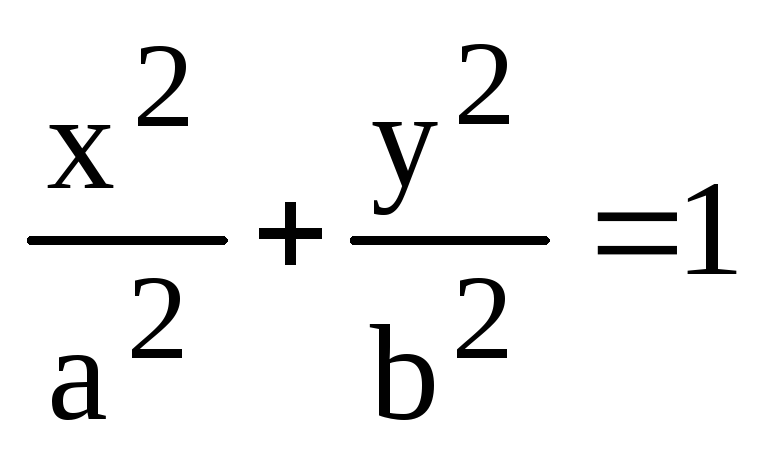В чём разница между эллипсом и овалом

Библиографический список

1. Чебыкин В.Г. Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых — «резервуарные» овалы. Справочник // Инженерный журнал. 2012. № 11. С. 31­33.
2. Чебыкин В.Г. Особенности технологии врезки люков и патрубков в обечайки резервуаров // Технология машиностроения. 2013. № 1. С. 33­35.
3. Чебыкин В. А не замахнуться ли нам на Габриеля нашего Ламе? // САПР и графика. 2013. № 8. С. 92, 94­95.
4. Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982. Т.5. С. 809.

Нижние индексы «co» означают циклоидальный овал (cycloidal oval).

Овал

Под овалом в геометрии понимается вытянутая замкнутая фигура правильной формы. Овал относится к двухмерным фигурам и обладает особыми свойствами. Само слово образовано от французского Ovale, которое, в свою очередь, имеет общие корни с латинской лексемой ovum, что в переводе означает «яйцо». Кривая этого геометрического объекта имеет с любой прямой не более двух общих точек.

Существует структурно более сложное понятие овала в инженерной графике. В этой отрасли науки данным термином обозначают фигуру, имеющую две оси симметрии и построенную при помощи сочетания четырёх участков кривых линий от двух радиусов. Эти участки подобраны таким образом, чтобы обеспечить «перетекание» от одного радиуса к другому без нарушения симметрии и контура фигуры. Если определять координаты точки, постоянно движущейся по линии овала, то она всегда будет находиться на одном из вышеописанных радиусов кривизны. Эти радиусы считаются «фиксированными».

Овальная кривая Rr

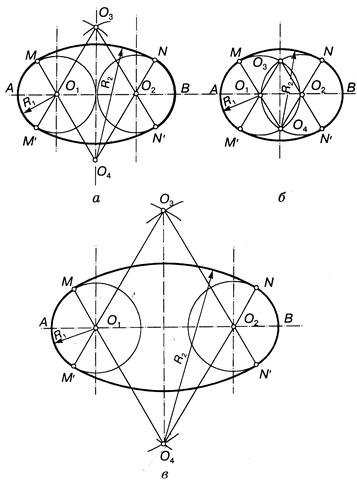
Овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1в и 3). Эти овалы хорошо известны тем, кто учился в докомпьютерную эру (по аналогии с «до н.э.» имеем «до к.э.»). Ими пользовались для упрощенного изображения эллипсов на чертежах. Сейчас, по понятным причинам, необходимость в этом отпала. В технике эти овалы все же используются — кулачки, эксцентрики и т.п.

На рис. 1в изображена овальная кривая Rr (гиперовал), а на рис. 3  —сразу три вида овалов: внутренний — гиперовал; наружный — гипоовал; средний — гипергипоовал. Тонкими линиями показаны соответствующие этим овалам эллипсы, которые помогают определить принадлежность кривых к той или иной группе.

Классификация кривых, описанных в статье :

• овал Кассини — гиперовал;
• кривая Ламе (показанная) — гипоовал;
• кривые R­0 и R­1 — гипоовалы;
• кривая R­2: верхняя часть — гиперовал, нижняя — гипоовал.

Идентификация эллипсовидных овальных кривых

Итак, для идентификации предлагаются следующие кривые: эллипс, овал Кассини, гиперэллипс Ламе; гипоэллипс Ламе; гипергипоэллипс Ламе; овал R­0; овал R­1; циклоидальный овал; гиперовал Rr; гипоовал Rr; гипергипоовал Rr. Зная геометрию и свойства данных кривых, классификацию можно выполнить визуально, однако иногда  некоторые из них бывают очень схожи.

Идентификацию лучше проводить в той CAD­программе, в которой эти кривые созданы. Автор для построения и идентификации кривых использовал  программу КОМПАС.

При поочередном входе в режим редактирования кривых можно сразу распознать эллипс и все овалы по сопрягаемым дугам окружностей, группу которых определяем сопряжением с эллипсом. Все остальные кривые при редактировании покажут, что построены с помощью кривой Безье.

Оставшиеся кривые сначала необходимо разбить на группы в соответствии с нашей классификацией путем сопряжения с соответствующими им эллипсами.

В группе гипергипоовалов окажется только гипергипоэллипс, так как гипергипоовал Rr распознан уже на первой стадии идентификации.

Далее рассмотрим группу гипоовалов. Поскольку гипоовал Rr также распознан на первой стадии, в ней остаются: кривая R­0; кривая R­1; гипоэллипс Ламе; циклоидальный овал. Последний распознаем с помощью эксцентриситет­константы циклоидального овала (пригодилась!). Для этого поочередно для каждой кривой рассчитываем фокальный радиус, умножая размер большой полуоси на эксцентриситет­константу Eco. Тот овал, в котором пучок из восьми лучей, выпущенных из фокуса и отраженных от кривой, соберется в противоположном фокусе, и будет циклоидальным овалом. Для распознавания оставшихся трех гипоовалов рассмотрим три возможных сценария идентификации. Все зависит от количества фокусов у гипоэллипса Ламе. Первый вариант — кривая Ламе имеет четыре фокуса (например, при сочетании параметров: a/b = 7/10; n = m = 1,7). В этом случае удается распознать все кривые: бесфокусную R­0, двухфокусную R­1 и четырехфокусную  кривую Ламе.  Второй вариант — кривая Ламе бесфокусная (например, при сочетании параметров: a/b = 8/10; n = m = 1,7). При этом сможем распознать только R­1. Кривая R­0 и гипоэллипс будут трудноразличимыми. Третий вариант — кривая Ламе имеет два фокуса (например, при сочетании параметров: a/b = 8/10; n = 1,7 и m=1,9). Выявить при этом удастся  только кривую R­0. Различить R­1 и гипоэллипс Ламе можно по форме кривых и расположению фокусов… 

Осталось разобраться с гиперовалами. После первой стадии идентификации, где был определен гиперовал Rr, их у нас осталось два: овал Кассини и гиперэллипс Ламе. Для идентификации их в первую очередь необходимо выровнять масштабированием размеров овалов по высоте. Далее нужно определить положение фокусов (тех, которые фигурируют в определении овала Кассини) относительно центра и нанести их. Оптические фокусы овалов использовать нельзя — у них другие координаты. Та кривая, на которой будет соблюдено следующее условие: произведение расстояний от любой точки кривой до фокусов есть величина постоянная, — и есть овал Кассини. Если степени гиперэллипса Ламе равны 2,5 и более, то кривые хорошо различимы визуально — кривая Ламе более угловатая.

Выводов делать не будем. Главное, что почти все точки над «о» расставлены. 

Циклоидальный овал

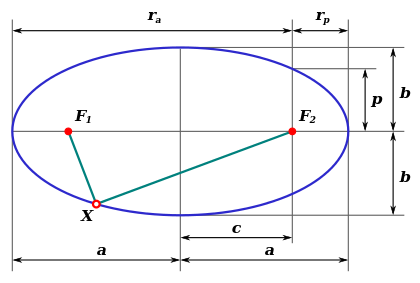
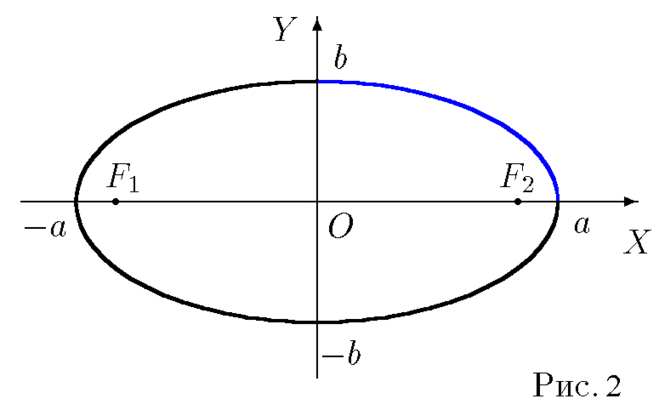
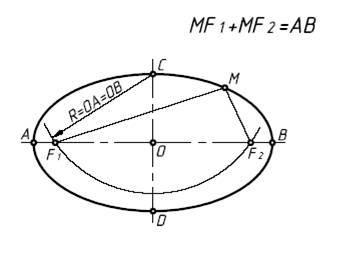
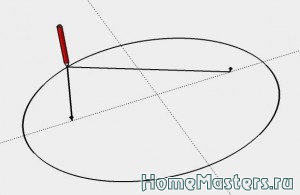
Циклоидальный овал (рис. 1а и 2) — это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая, полученная в результате зеркальной стыковки двух «арок» циклоиды. Циклоида — плоская трансцендентная кривая; это траектория точки окружности, катящейся по прямой линии .

Одним из свойств циклоидального овала является наличие двух фокусов, имеющих строго определенное расположение.

Фокусы могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. Это свойство совпадает с аналогичным у кривой R­1, описанной в . Точки падения этих лучей на кривую, так же как у кривой R­1, являются характерными — в них меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный.

Еще одно свойство циклоидального овала: размеры некоторых элементов овала могут быть вычислены как произведение радиуса производящей окружности данной циклоиды или размеров полуосей с определенными константами. О последних и пойдет речь далее.

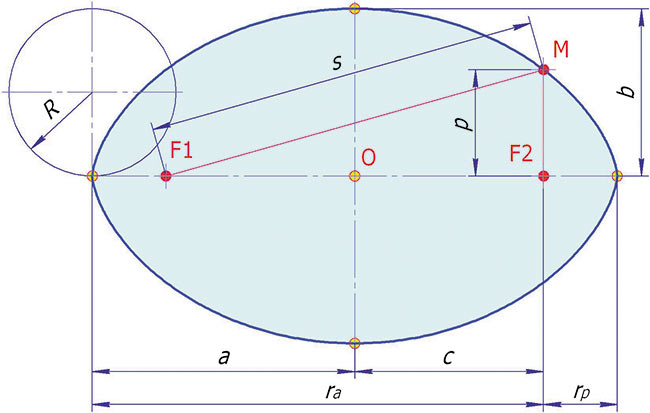
Рис. 2. Циклоидальный овал

Элементы овала (рис. 2):

• R — радиус производящей окружности цик­лоиды;
• a — большая полуось;
• b — малая полуось;
• с — фокальный радиус (полурасстояние между фокусами);
• p — малый фокальный луч;
• s — большой фокальный луч;
• rp — перифокусное расстояние (минимальное расстояние от фокуса до точки на овале);
• ra — апофокусное расстояние (максимальное расстояние от фокуса до точки на овале).

Константы циклоидального овала:

1. Константа соотношения осей овала
   Ксо = а/b = p/2;
2. Фокальная константа
   Vco = c/R ≈ 2,259 360 664 54…;
3. Перифокусная константа
   PVco = rp/R ≈ 0,882 231 989 04…;
4. Апофокусная константа
   AVco = ra/R ≈ 5,400 953 318 13…;
5. Эксцентриситет­константа
   Eco = с/a ≈ 0,719 176 835 98…;
6. Константа малого фокального луча
   Lco = p/R ≈ 1,270 684 347 65…;
7. Константа большого фокального луча
   GLco = s/R ≈ 4,693 983 506 71…

Попытка найти в литературе и Интернете сведения по константам циклоидальных овалов ничем не увенчалась, поэтому названия констант и их обозначения автор предложил свои. Ну и значения констант, за исключением первой, пришлось определить самому.

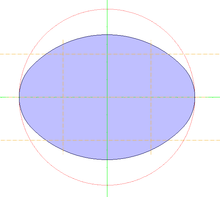
Теперь отнесем этот овал к одной из групп: гиперовалы (от греч., гипер —  «над, выше»); гипоовалы (гипо — «под, ниже»); гипергипоовалы.

Построим по полюсам данного овала эллипс и увидим, что он будет описанным по отношению к овалу, а овал соответственно — вписанным в эллипс. Исходя из этого, циклоидальный овал является гипоовалом. Циклоидальные кривые используются в технике: маятник Гюйгенса; кривая кратчайшего спуска; циклоидальные передачи и редукторы; кулачки и эксцентрики…