Тупоугольный треугольник, элементы, свойства, признаки и формулы

Свойства

• Задача Фаньяно. Ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.
• Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
• Если точки A₁, B₁ и C₁ на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

∠BA1C1=∠CA1B1{\displaystyle \angle BA_{1}C_{1}=\angle CA_{1}B_{1}} , ∠CB1A1=∠AB1C1{\displaystyle \angle CB_{1}A_{1}=\angle AB_{1}C_{1}} и ∠AC1B1=∠BC1A1{\displaystyle \angle AC_{1}B_{1}=\angle BC_{1}A_{1}},

то A1B1C1{\displaystyle A_{1}B_{1}C_{1}} — ортотреугольник треугольника ABC.

Если вокруг данного остроугольного треугольника описать окружность и в трех вершинах треугольника провести прямые, касательные к окружности, то пересечение этих прямых образует треугольник, который называют тангенциальным треугольником по отношению к данному треугольнику.

Свойства подобия родственных треугольников

Исходный треугольник ΔABC{\displaystyle \Delta ABC} по отношению к ортотреугольнику является треугольником трех внешних биссектрис.

△A1B1C1{\displaystyle \triangle A_{1}B_{1}C_{1}} — ортотреугольник треугольника △ABC{\displaystyle \triangle ABC}, а △A2B2C2{\displaystyle \triangle A_{2}B_{2}C_{2}}— треугольник Жергонна ортотреугольника. H{\displaystyle H}— ортоцентр △ABC{\displaystyle \triangle ABC}, инцентр △A1B1C1{\displaystyle \triangle A_{1}B_{1}C_{1}}и центр описанной окружности △A2B2C2{\displaystyle \triangle A_{2}B_{2}C_{2}}. Треугольники △ABC{\displaystyle \triangle ABC} и △A2B2C2{\displaystyle \triangle A_{2}B_{2}C_{2}} подобны.

• Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
• Треугольник Жергонна ортотреугольника и исходный треугольник подобны (см. рисунок).
• Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
• Ортотреугольник треугольника Жергонна и исходный треугольник подобны.
• Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности (антипараллельности) сторон родственных треугольников.

Свойства параллельности (антипараллельности) сторон родственных треугольников

• Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
• Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
• Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
• Если точки касания вписанной в данный треугольник окружности соединены отрезками, то получится треугольник Жергонна. Пусть в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно, ортотреугольник треугольника Жергонна и исходный треугольник подобны.

Другие свойства

Площадь ортотреугольника равна:

Sort=S(2abc)2(a2+b2−c2)(a2+c2−b2)(b2+c2−a2){\displaystyle S_{ort}={\frac {S}{(2abc)^{2}}}(a^{2}+b^{2}-c^{2})(a^{2}+c^{2}-b^{2})(b^{2}+c^{2}-a^{2})}

где S{\displaystyle S} — площадь треугольника ΔABC; a,b,c{\displaystyle a,b,c} — его соответствующие стороны.

• Окружность, описанная около ортотреугольника Δabc, для самого треугольника ΔABC является окружностью Эйлера (окружностью 9 точек), то есть одновременно проходит, через 3 основания медиан последнего. Заметим, что эти 3 основания медиан являются вершинами дополнительного треугольника для треугольника ΔABC.
• Радиусы окружности, описанной около данного треугольника ΔABC, проведенные через его вершины, перпендикулярны соответственным сторонам ортотреугольника Δabc (Зетель, следствие 2, § 66, с. 81).

Ортоцентр треугольника

      Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.

      Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, противолежащей стороне (рис.3).

Рис.3

      Обозначим точки пересечения этих прямых символами A₁, B₁ и C₁, как показано на рисунке 3.

      В силу параллельности прямых AC и C₁A₁, а также BC и C₁B₁ четырёхугольники   AC₁BC   и   ABA₁C – , откуда

C₁B = AC = BA₁.

      Следовательно, точка B является серединой стороны C₁A₁.

      В силу параллельности прямых BC и C₁B₁, а также AB и B₁A₁ четырёхугольники   AC₁BC   и   ABCB₁ – ,, откуда

C₁A = BC = A₁B₁.

      Следовательно, точка A является серединой стороны C₁B₁.

      В силу параллельности прямых AB и B₁A₁, а также AC и C₁A₁ четырёхугольники   ABA₁C   и   ABCB₁ – , откуда

A₁C = AB = B₁C.

      Следовательно, точка C является серединой стороны B₁A₁.

      Таким образом, высоты треугольника ABC являются треугольника A₁B₁C₁ (рис. 4),

Рис.4

и в силу пересекаются в одной точке.

      Теорема 1 доказана.

      Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.

      У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.

Пример решения задачи

В тупоугольном треугольнике АВС известно, что косинус тупого угла равен $-2/\sqrt{13}$. Сторона АС находится напротив тупого угла, $АВ=\sqrt{13}$, ВС=2. Необходимо найти внешнюю высоту треугольника АМ.

Рис. 3. Рисунок к задаче.

Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.

Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.

$$sin(ABC)=\sqrt{1-cos(ABC)^2}=\sqrt{1-4 \over13}=\sqrt{9 \over13}={3\over\sqrt{13}}$$

Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.

$$S={1\over2}*AM*BC$$

$$S={1\over2}*AB*BC sin(ABC)$$

$${1\over2}*AM*BC={1\over2}*AB*BC*sin(ABC)$$

$$AM*ВС=AB*BC*sin(ABC)$$

$$AM=AB*sin(ABC)$$

$$AM=\sqrt{13}*{3 \over \sqrt{13}}=3$$

$$Cos(ABC)=cos(ABC-180)=-cos(180-ABC)=-cos(ABM)$$

$$Cos(ABM)=-cos(ABC)={2\over \sqrt{13}}$$

Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.

$$Sin(ABM)=\sqrt{1-cos(ABM)^2}=\sqrt{1-4\over13}=\sqrt{9\over13}={3\over\sqrt{13}}$$

$$Sin(ABM)=AM/AB$$

$$AM=AB*sin(ABM)=\sqrt{13}*{3\over\sqrt{13}}=3$$

$$АС=\sqrt{AB^2+BC^2-AB*BC*cos(ABC)}=$$

$$\sqrt {\sqrt{13}^2+2^2-\sqrt{13}*2*{-2\over\sqrt{13}}}=$$

$$\sqrt{13+4+4}=\sqrt{21}=\sqrt{9*3}=3\sqrt{3}$$ – по теореме косинусов.

$${АС\over{sin(ABC)}}={AB\over{sin(ACB)}}$$ – по теореме синусов.

Значение синуса угла АВС определим по основному тригонометрическому тождеству.

$$ Sin(ABC)=\sqrt{1-cos(ABC)^2}=\sqrt{1-{4\over{13}}}=\sqrt{9\over{13}}={3\over\sqrt{13}}$$

Выразим искомый синус угла АСВ.

$$Sin(ACB)=AB*{sin(ABC)\over{AC}}$$

$$Sin(ACB)=(\sqrt{13}*{{3\over\sqrt{13}}\over{3\sqrt{3}}})={1\over\sqrt{13}}$$

Выразим из треугольника АМС и найденного значения синуса сторону АМ.

$$Sin(ACB)={AM\over AC}$$

$$AM=sin(ACB)*AC$$

$$AM={1\over\sqrt{13}}*{3\over\sqrt{13}}=3$$

Ответы всех трех способов совпали, а значит задача решена верно.

Что мы узнали?

Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а так же выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.

Серединный перпендикуляр и описанная окружность треугольника

Рассмотрим практическую задачу. Пусть у нас есть три поселка . И нужно разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка (см. рис. 33). Понятно, что станция должна быть расположена так, чтобы расстояние от нее до каждого из трех поселков было одинаковым.

Рис. 33. Необходимо разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка

Сначала решим более простую задачу. Пусть поселков всего два – и (отрезок ). Где должна быть расположена станция в этом случае?

Рассмотрим прямую, которая проходит через середину отрезка и перпендикулярна ему. Эта линия называется серединным перпендикуляром

(см. рис. 34).

Рис. 34. Серединный перпендикуляр к отрезку

Рассмотрим любую точку , которая принадлежит серединному перпендикуляру . Треугольники и равны по первому признаку равенства треугольников (два катета и угол между ними): , т. к. – середина , – общая, . Значит, (см. рис. 35).

Рис. 35. Равные треугольники и

Несложно доказать, что любая точка, например , которая не лежит на серединном перпендикуляре, не будет удовлетворять этому свойству, т. е. (см. рис. 36).

Рис. 36. Точка , – серединный перпендикуляр:

Доказательство

Как доказать, что любая точка, которая не лежит на серединном перпендикуляре, не равноудалена от концов отрезка? Снова воспользуемся методом от противного.

Пусть точка не лежит на серединном перпендикуляре к отрезку , но при этом она равноудалена от концов отрезка: (см. рис. 37).

Рис. 37. Точка – серединный перпендикуляр к ,

Соединим точку с серединой отрезка – точкой . Рассмотрим треугольники и .

Рис. 38. Рассматриваемые треугольники и

В них: (по нашему предположению), , т. к. – середина отрезка , – общая. По третьему признаку треугольника (три стороны) треугольники и равны.

Но тогда : они смежные (т.е. образуют развернутый угол и их сумма равна ). Значит, . Но тогда прямая перпендикулярна отрезку и проходит через его середину. Значит, – серединный перпендикуляр к отрезку .

Получаем противоречие (точка не должна лежать на серединном перпендикуляре). Значит, исходное предположение неверно, и если точка не лежит на серединном перпендикуляре, то она не будет равноудалена от концов отрезка.

Сформулируем эквивалентное определение серединного перпендикуляра

– это геометрическое место точек (ГМТ), равноудаленных от концов отрезка.

Понятно, что станция скорой помощи должна располагаться на серединном перпендикуляре к отрезку (в идеале – в точке , середине отрезка, т. к. в этом случае расстояние от нее до точек и будет наименьшим).

Формулы площади треугольника

1.Произвольный треугольник – формулы площади

a, b, c — стороны; α — угол между сторонами a и b; p=(a+b+c) / 2— полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h_a — высота, проведенная к стороне a.

1. S=(1/2)*(a* h_a) – по стороне и высоте.
2. S=(1/2) *(a*b*sinα) по двум сторонам и синусу угла между ними
3. Прямоугольный треугольник – площадь

   a, b — катеты; c — гипотенуза; h_c — высота, проведенная к стороне c.

   Примечание – в прямоугольном треугольнике:

   – Синус α – это отношение AB/OB (отношение противолежащего катета к гипотенузе)

   – Косинус α – это отношение ОА/OB (отношение прилежащего катета к гипотенузе)

   – Тангенс α – это отношение AB/OA (отношение противолежащего катета к прилежащему)

   – Котангенс α – это отношение ОА/AB (отношение прилежащего катета к противолежащему)

   “>

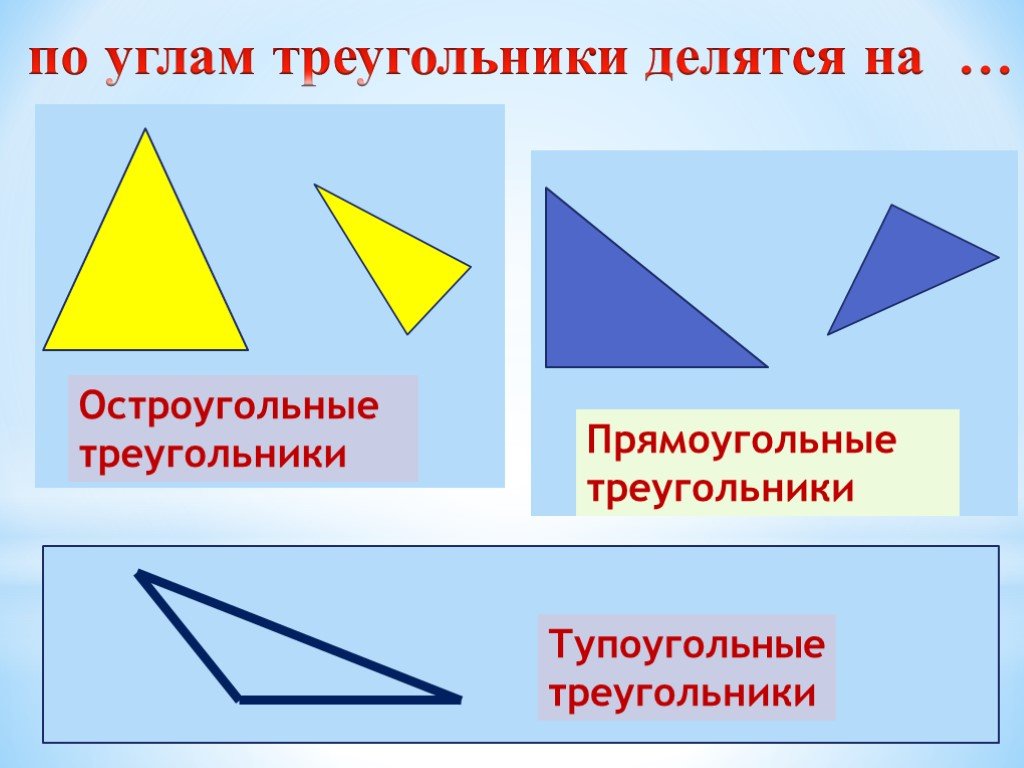
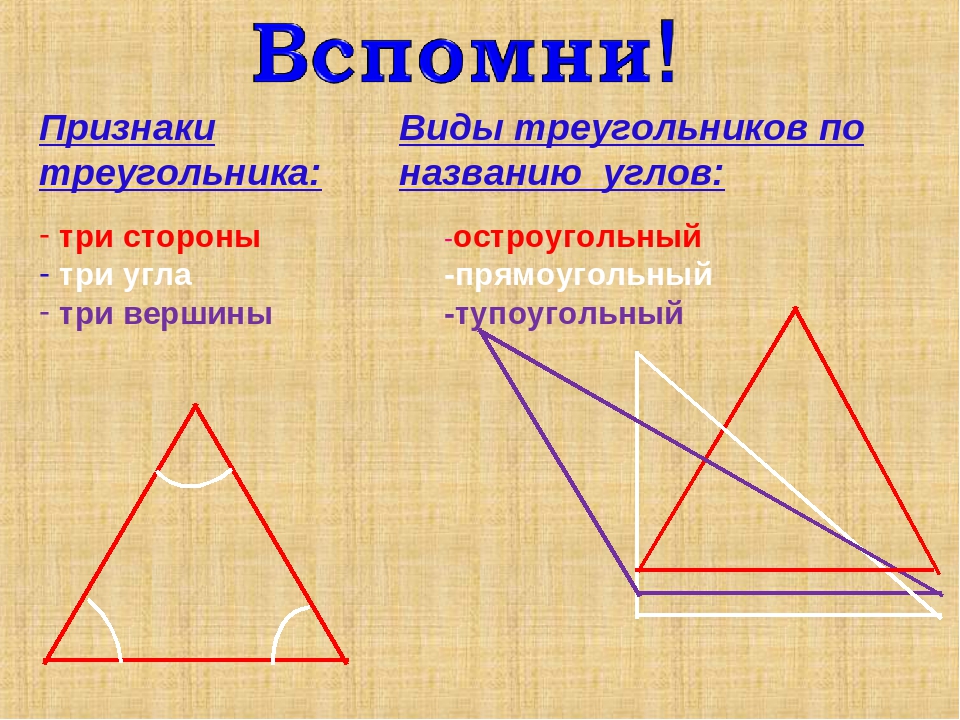
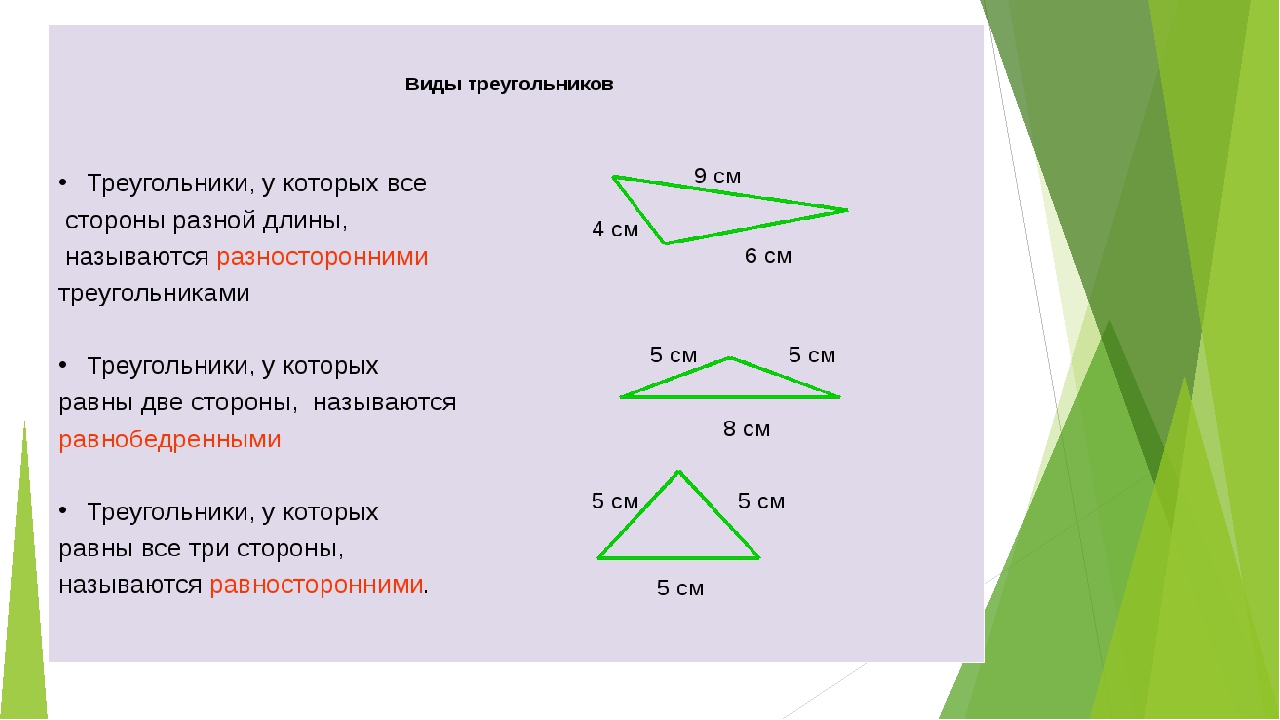
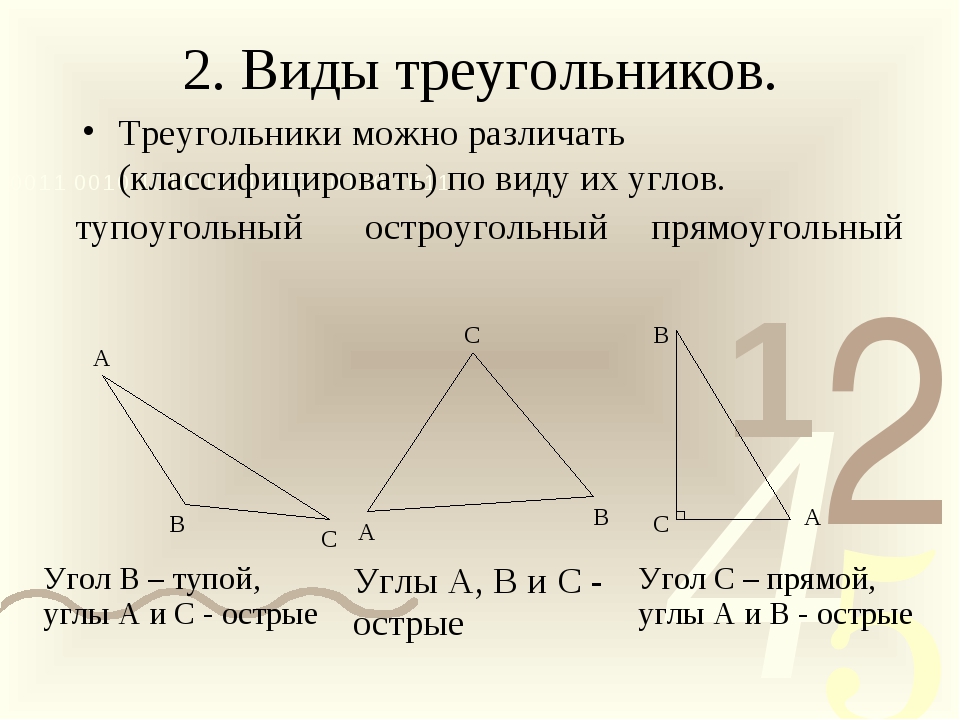
Виды треугольников:

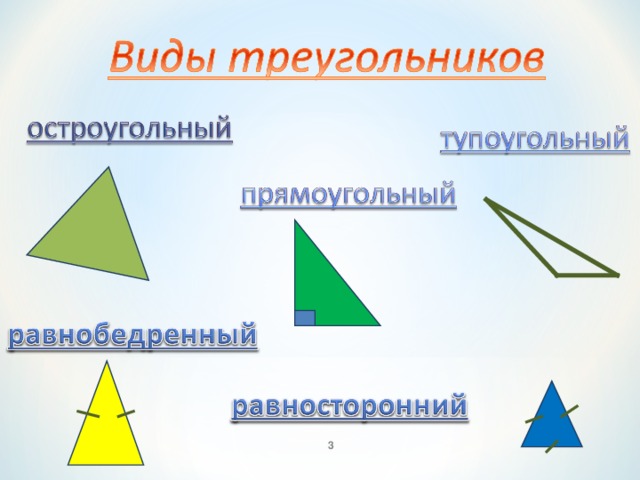
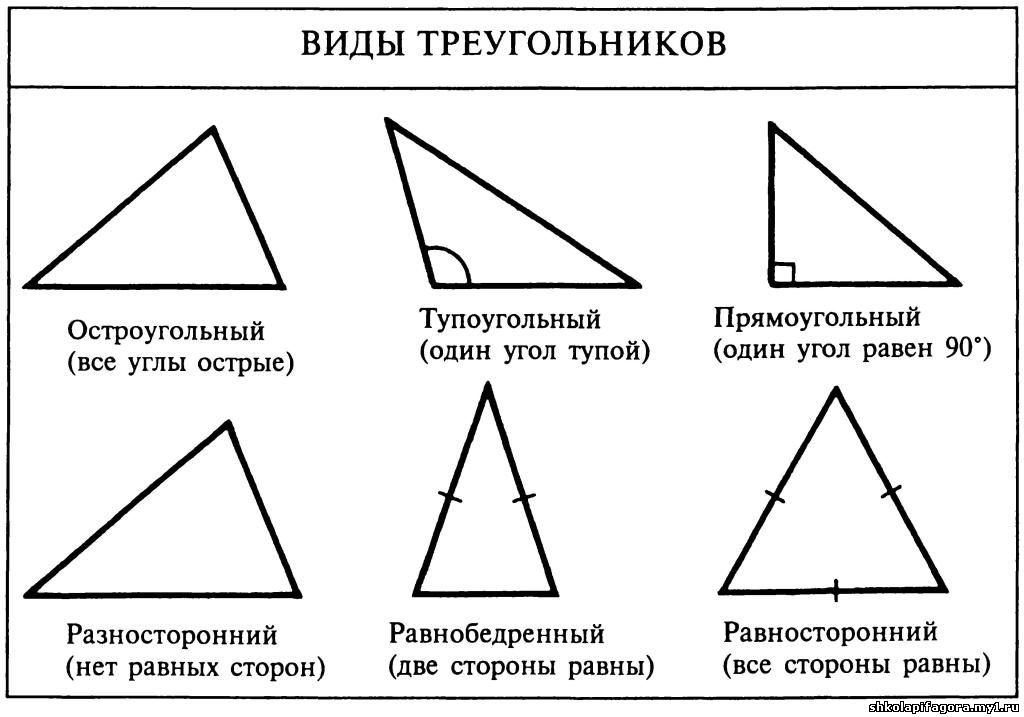
(по величине углов)

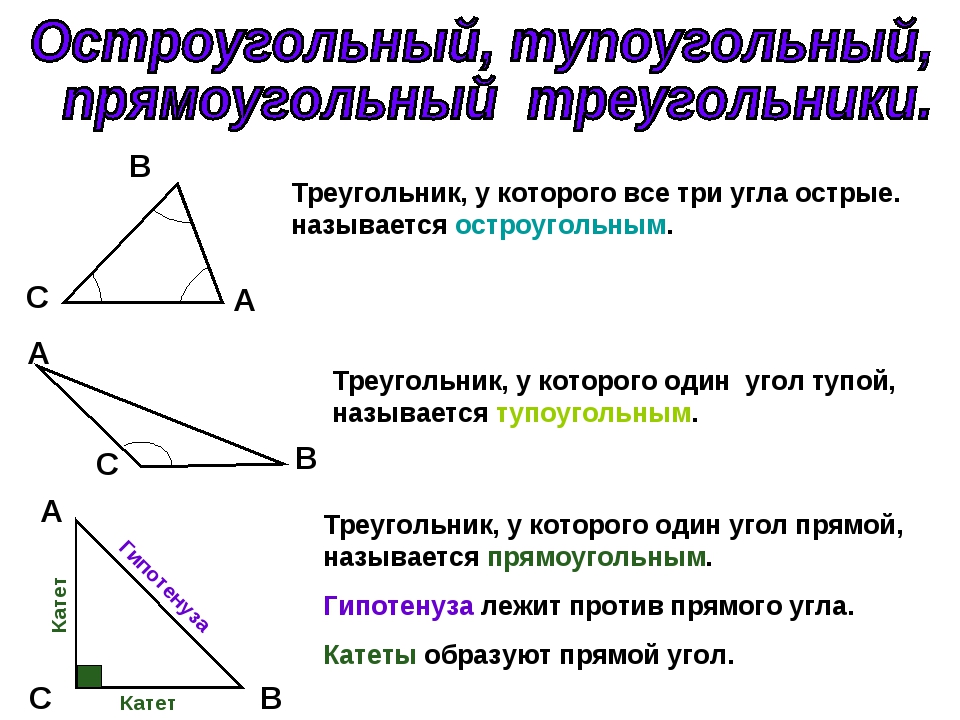
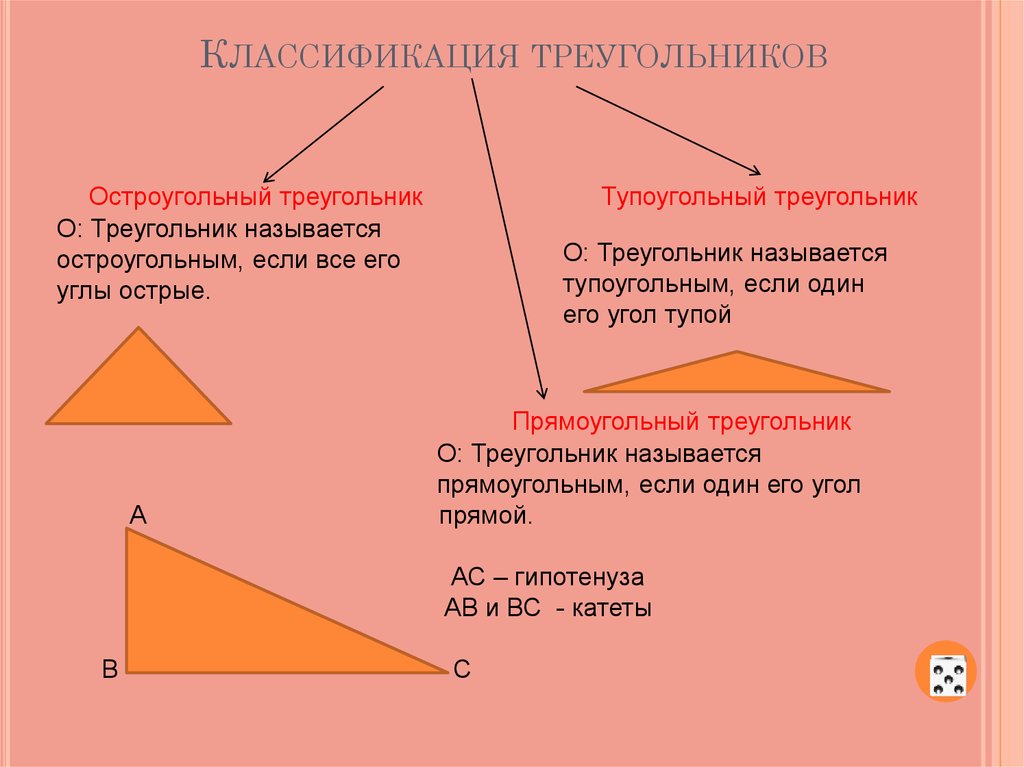
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.

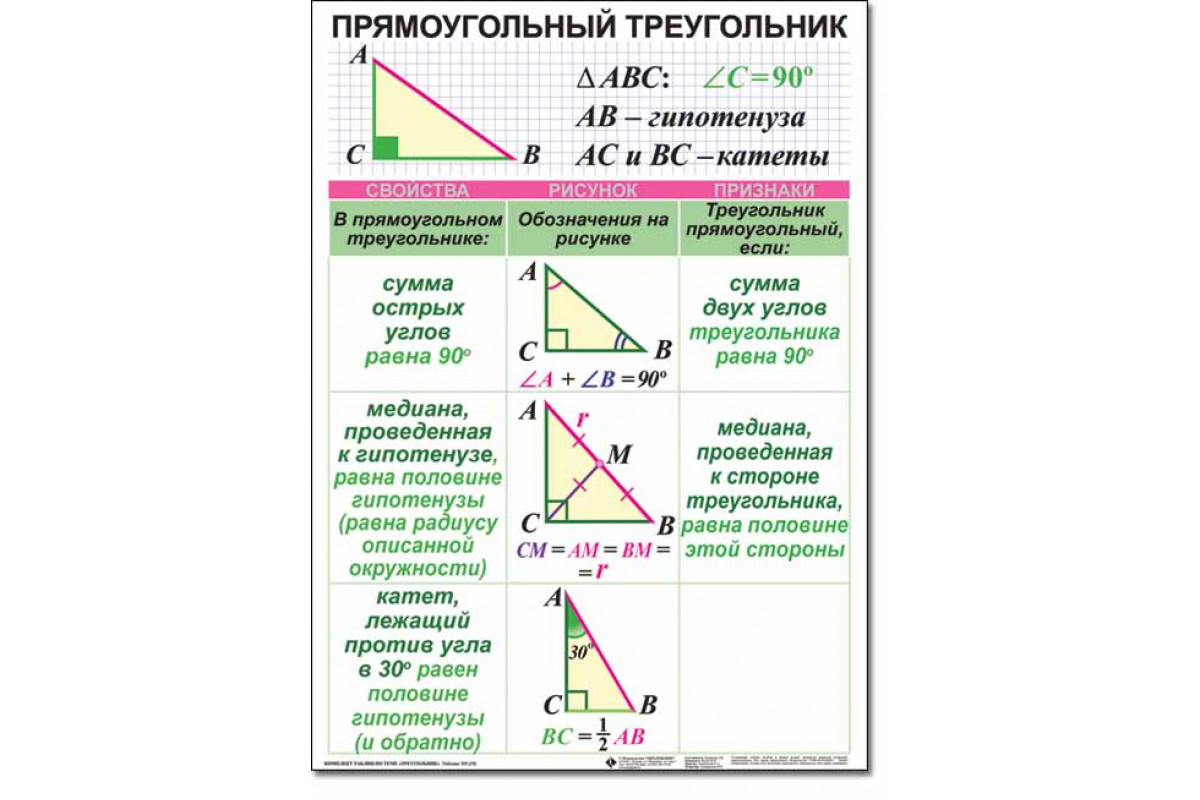
Прямоугольный треугольник – это треугольник, содержащий прямой угол.

Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).

Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.

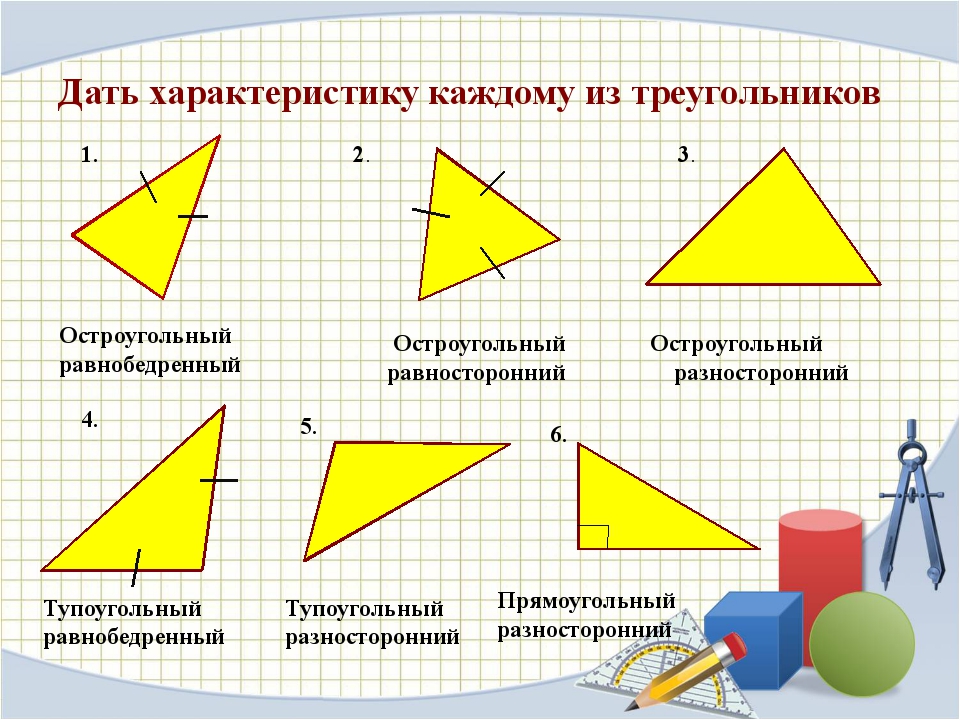
(по числу равных сторон)

(по соотношению сторон)

Равносторонний (правильный) треугольник – это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°).

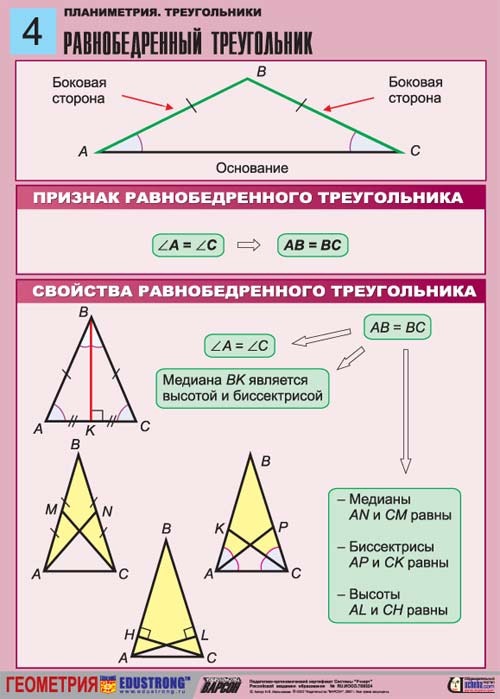
Равнобедренный тругольник – это треугольник, у которого два угла и две стороны равны.

Разносторонний треугольник – это треугольник, в котором все углы, а значит и все стороны попарно различны.

(Разносторонний треугольник может быть остроугольным, прямоугольным и тупоугольным).

Рассмотрим рис. ниже.

Углы α, β, γ нызываются внутренними углами треугольника.

Угол Θ – называется внешним углом треугольника, он равен сумме двух противолежащих ему внутренних углов, т.е. Θ= β+γ

(а+с+b) – периметр треугольника.

Угол α, называется смежным по отношению к углу Θ. ( α+ Θ)=180° (развернутый угол)

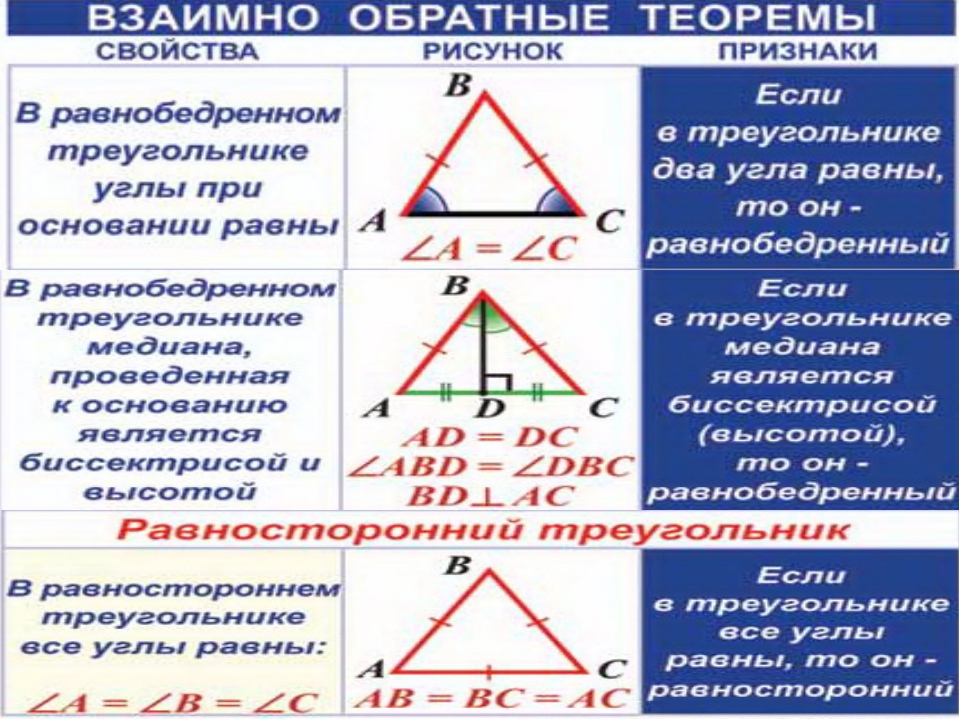
Основные свойства треугольников. В любом треугольнике:

Против большей стороны лежит больший угол, и наоборот.

Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)

Сумма углов треугольника равна 180 ° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60 °).

Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.

Любая сторона треугольника меньше суммы двух других сторон и больше их разности:

• a b – c;
• b a – c;
• c a – b.

• Треугольник
• Обозначения в треугольнике
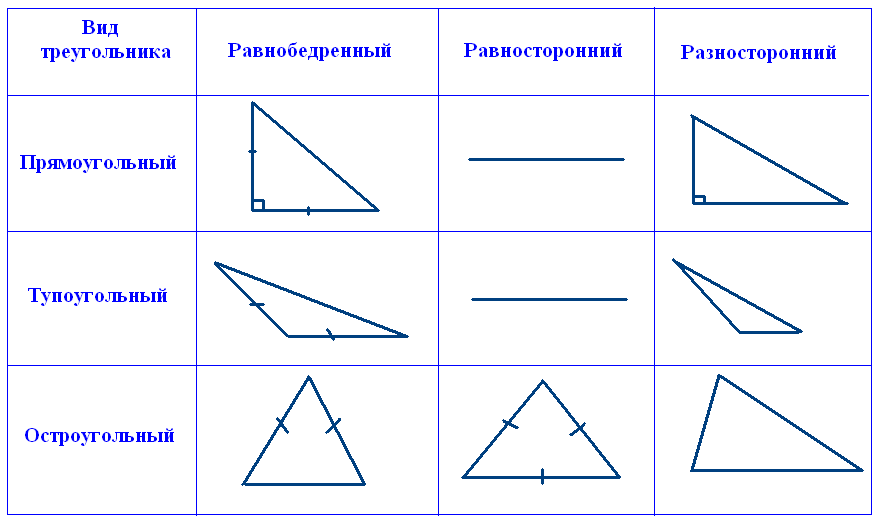
• Виды треугольников
• Основные свойства треугольников
• Конгруэнтные (равные) треугольники
• Признаки равенства треугольников
• Признаки равенства прямоугольных треугольников
• Подобные треугольники
• Признаки подобия треугольников
• Свойства подобных треугольников

• Подобие в прямоугольных треугольниках
• Теорема Пифагора
• Теорема синусов
• Теорема косинусов
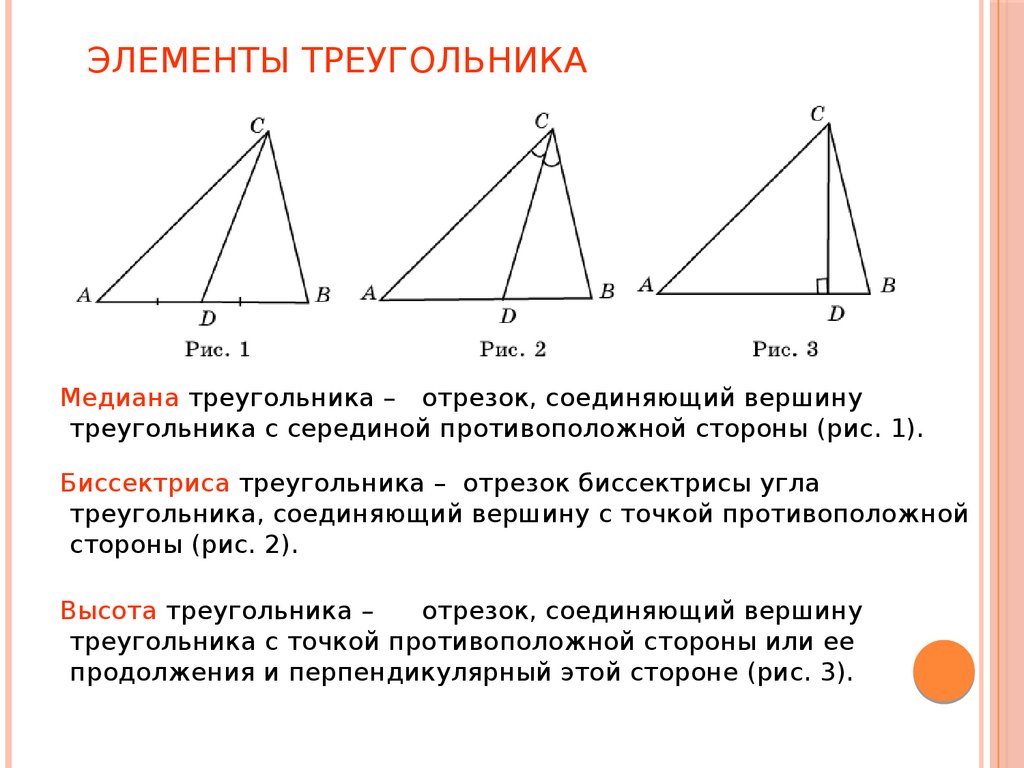
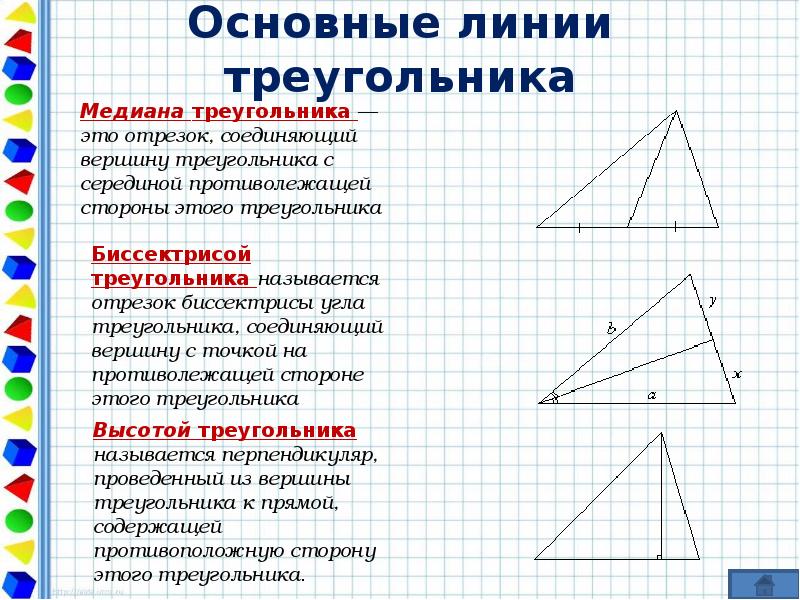
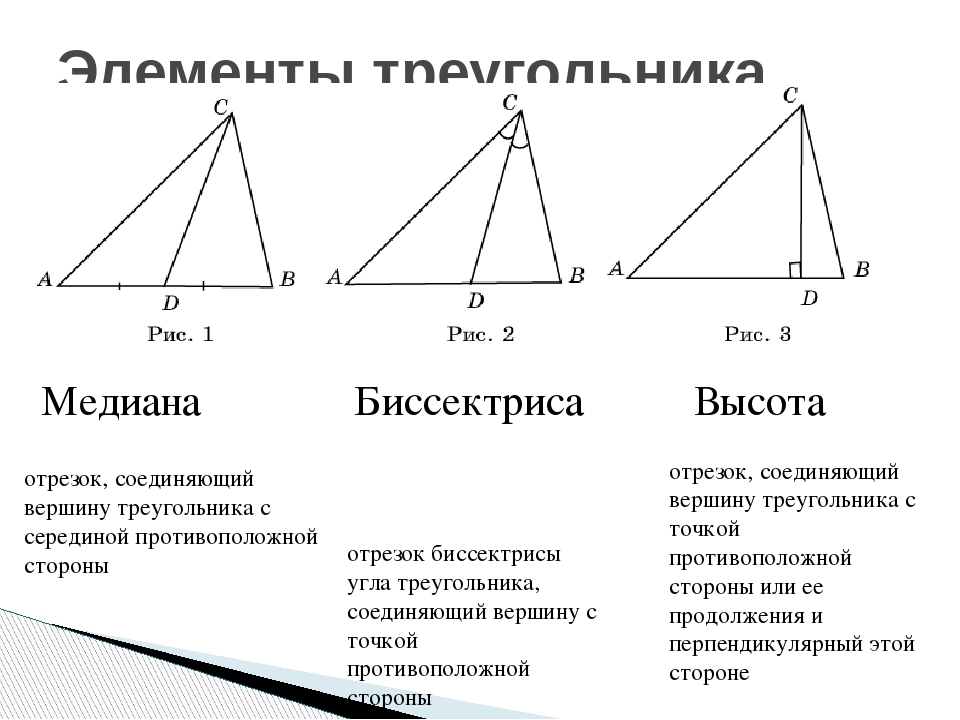
• Медиана
• Биссектриса
• Высота треугольника
• Срединный перпендикуляр
• Средняя линия треугольника
• Формулы площади треугольника, в т.ч. Герона
• Окружности вписанные в треугольники и описанные вокруг треугольников.

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

АВ = АС

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

Как возможно научиться писать тексты и зарабатывать на этом удаленно? Например, можете пройти курс «Копирайтинг от А до Я», который подойдет даже начинающим авторам.

Другие записи:

карта сайта

Коэффициент востребованности
2 424

Виды треугольников

Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.

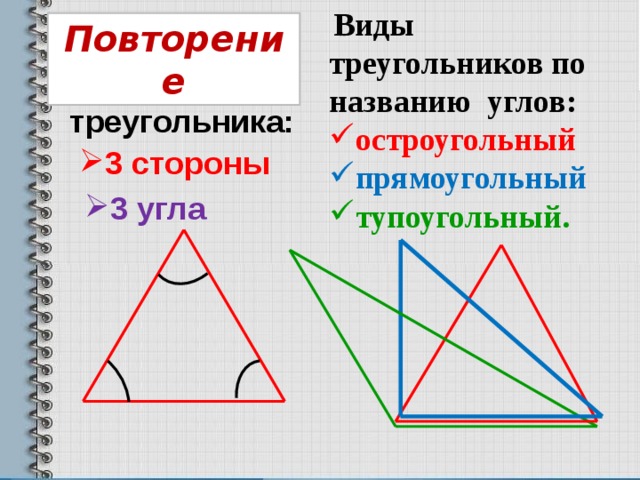
Существует три вида треугольников по углам:

• остроугольные;
• прямоугольные;
• тупоугольные.

Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .

Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.

Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.

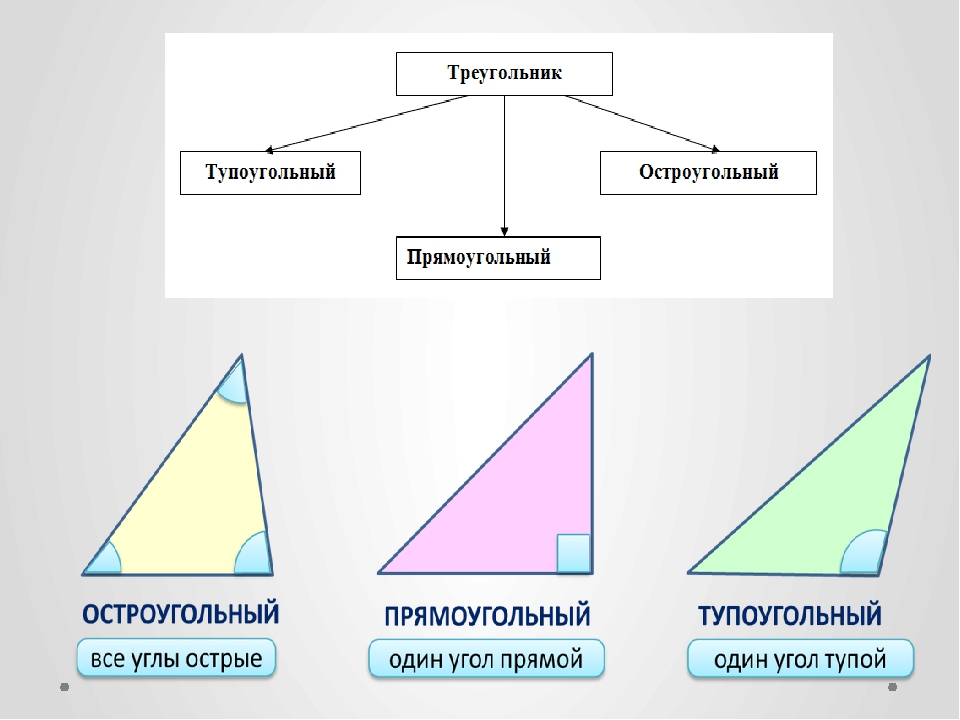
Рис. 2. Виды треугольников по углам.

Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.

Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.

Виды треугольников по сторонам:

• равносторонние;
• равнобедренные;
• разносторонние.

Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.

Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.

Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.

Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.

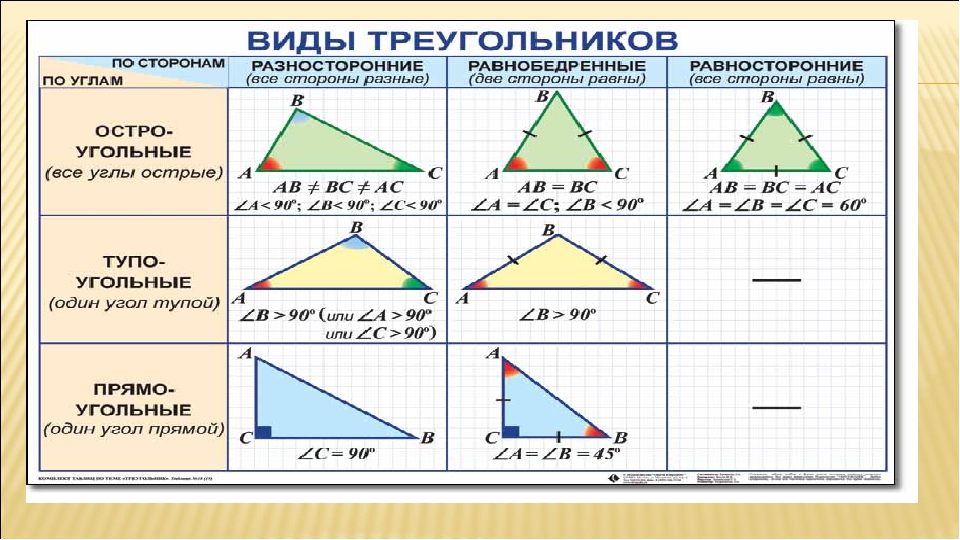
Рис. 3. Виды треугольников по сторонам.

Сумма всех углов треугольника, независимо от его вида, равна 1800.

Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.

Задача:

Существует ли треугольник, стороны которого равны 6 см., 3 см., 4 см.?

Решение:

Для решения данного задания нужно использовать неравенство a

Средняя оценка: 4.4 . Всего получено оценок: 160.

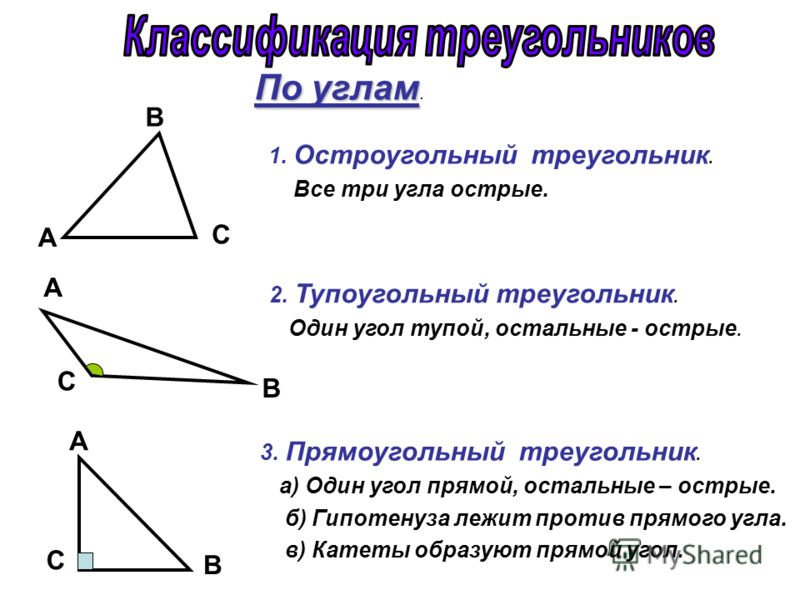
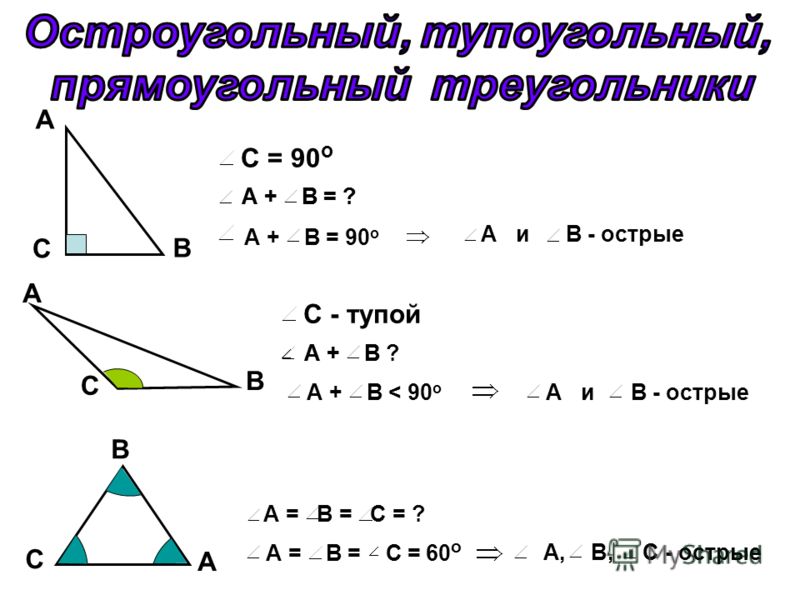
В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

• остроугольные
• прямоугольные
• тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

• равносторонние
• равнобедренные
• разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

Свойства треугольников.

Меню

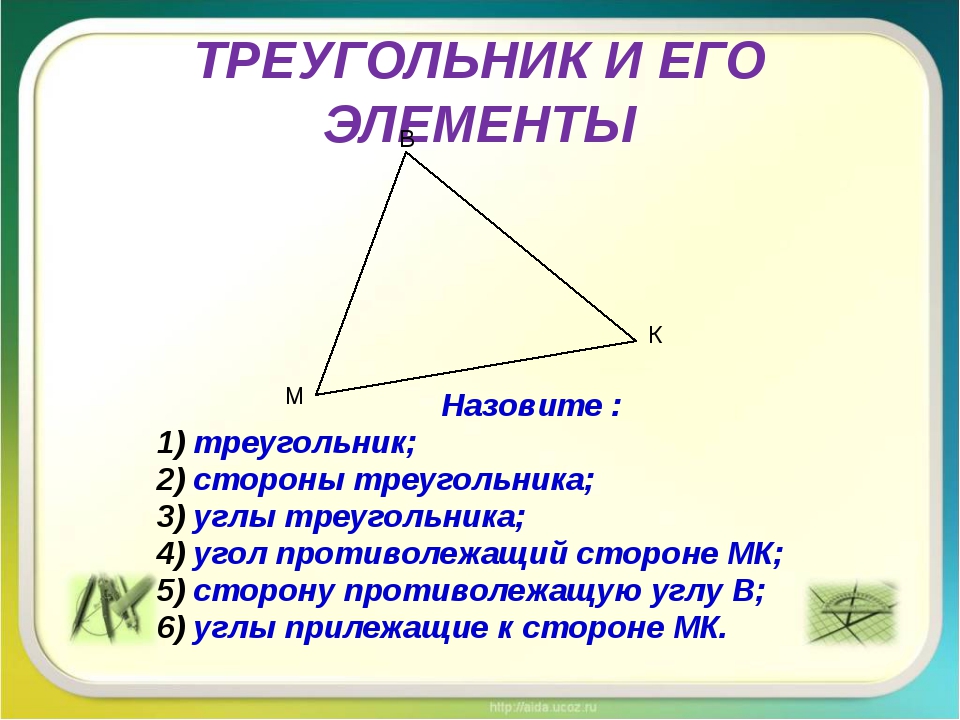
Треугольник -это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами.

Для инженера это еще и единственная «жесткая» плоская фигура на свете.

Раздел математики, посвященный изучению закономерностей треугольников — тригонометрия.

Сумма всех углов в треугольнике равна 180°.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Задача Фаньяно

      Задача Фаньяно. Рассматриваются всевозможные треугольники   DEF,   вершины    D,   E   и   F   которых лежат на сторонах   BC,   AC и   AB     ABC   соответственно. Доказать, что из всех треугольников DEF наименьшим  обладает ортоцентрический треугольник треугольника   ABC.

      Решение. Пусть   DEF – один из рассматриваемых треугольников. Обозначим символом   D₁   точку, , и обозначим символом   D₂   точку,  (рис.8).

Рис.8

      Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D₁D₂. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D₁D₂ с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D₁D₂ (рис.9).

Рис.9

      Заметим также, что выполнено равенство

AD = AD₁ = AD₂.

      Кроме того, выполнено равенство

      Поэтому

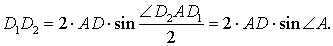
      Отсюда вытекает, что длина отрезка D₁D₂ будет наименьшей тогда, когда длина отрезка AD  будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF  треугольник с наименьшим периметром является единственным.

      Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус буквами h, c и R соответственно, то, воспользовавшись , получим:

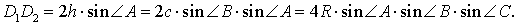
      Следовательно, наименьший периметр рассматриваемых треугольников DEF равен

      Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.

      Лемма. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).

Рис.10

      В этом случае отрезок D₁D₂  проходит через точки F и E.

      Доказательство. Заметим, что в силу выполняются равенства:

      Кроме того, в силу DFK и KFD₂, а также в силу DEL и LED₁ выполняются равенства:

      Следовательно,

откуда вытекает, что углы AEF и D₁EL , а также AFE и D₂FK являются . Это означает, что точки D₁, F, E, D₂ лежат на одной прямой. Лемма доказана.

      Доказательство леммы и завершает решение задачи Фаньяно.

Линии остроугольного треугольника

Остроугольный треугольник обладает рядом свойств.

Медиана будет равняться половине длины той стороны геометрической фигуры, на которую она опущена. Причем можно провести этот отрезок с любой вершины.

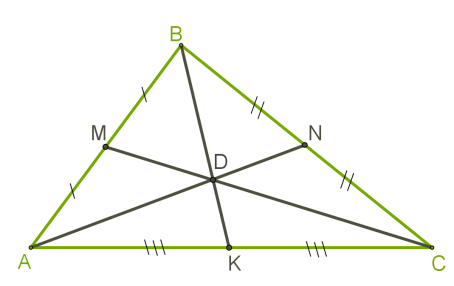
Рис. 1. Медианы в остроугольном треугольнике

Известно, что если провести три высоты в остроугольном треугольнике, то они будут пересекаться в одной точке, которую называют ортоцентром. Эти отрезки опускают под прямым углом к противоположным сторонам. Высоты в остроугольном треугольнике разделяют эту фигуру на подобные треугольники.

Рис. 2. Высоты в остроугольном треугольнике

Биссектрисы в остроугольном треугольнике не только делят углы пополам. Эти отрезки пересекаются в точке, которая является центром вписанной окружности.

Также биссектриса разделяет сторону остроугольного треугольника на две части, которые пропорциональны соответствующим сторонам. Данное утверждение нужно запомнить, чтобы решать некоторые задачи.

Рис. 3. Биссектрисы в остроугольном треугольнике