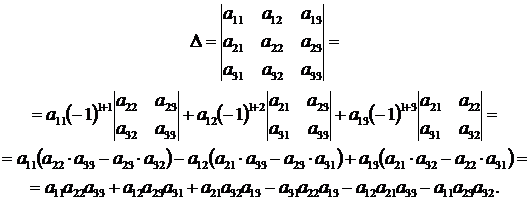Свойства определителя.
Среди наиболее важных свойств определителя назовем следующие.
(i) Если все элементы любой строки (или любого столбца) равны нулю, то и значение определителя равно нулю:
(ii) Если элементы двух строк (или двух столбцов) равны или пропорциональны, то значение определителя равно нулю:
(iii) Значение определителя не изменится, если все его строки и столбцы поменять местами, т.е. записать первую строку в виде первого столбца, вторую строку – в виде второго столбца и т.д. (такая операция называется транспонированием). Например,
(iv) Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на произвольный множитель. В следующем примере элементы второй строки умножаются на –2 и прибавляются к элементам первой строки:
(v) Если поменять местами две строки (или два столбца), то определитель изменит знак:
(vi) Если все элементы одной строки (или одного столбца) содержат общий множитель, то этот множитель можно вынести за знак определителя:
Пример. Вычислим значение следующего определителя 4-го порядка:
Прибавим к 1-й строке 4-ю строку:
Вычтем 1-й столбец из 4-го столбца:
Умножим 3-й столбец на 3 и вычтем из 4-го столбца:
Если угодно, то строки и столбцы можно поменять местами:
Разложим определитель по элементам четвертой строки. Три элемента этой строки равны нулю, ненулевой элемент стоит в третьем столбце, а поскольку сумма (3 + 4) нечетна, его алгебраическое дополнение имеет знак минус. В результате получаем:
Минор можно разложить по элементам третьей строки: два ее элемента равны нулю, а отличный от нуля элемент стоит в третьем столбце; сумма (3 + 3) четна, поэтому предыдущее равенство можно продолжить:

Смотри также
В Викисловаре есть статья «оракул»
Квантовый оракул
Основные свойства определителя
В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было?
Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя:
- Если поменять две строчки (столбца) местами, определитель не изменится;
- Если одну строку (столбец) умножить на число $k$, то весь определитель тоже умножится на число $k$;
- Если взять одну строку и прибавить (вычесть) её сколько угодно раз из другой, определитель не изменится;
- Если две строки определителя одинаковы, либо пропорциональны, либо одна из строк заполнена нулями, то весь определитель равен нулю;
- Все указанные выше свойства верны и для столбцов.
- При транспонировании матрицы определитель не меняется;
- Определитель произведения матриц равен произведению определителей.
Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули.
Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше.
Давайте посмотрим, как это работает на практике:
Парочка замечаний перед тем, как мы перейдём к последней задаче:
- Исходная матрица была симметрична относительно побочной диагонали. Все миноры в разложении тоже симметричны относительно той же побочной диагонали.
- Строго говоря, мы могли вообще ничего не раскладывать, а просто привести матрицу к верхнетреугольному виду, когда под главной диагональю стоят сплошные нули. Тогда (в точном соответствии с геометрической интерпретацией, кстати) определитель равен произведению ${{a}_{ii}}$ — чисел на главной диагонали.
Идём дальше. Последняя задача в сегодняшнем уроке.
Всё. Хорош читать этот бред.:)
- Обратная матрица
- Умножение матриц
- Пробный ЕГЭ-2011 по математике, вариант №2
- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)
- Задача B8: отрезки и углы в треугольниках
- Задача B5: площадь фигуры без клеток
Свойства определителя матрицы
- Определитель равен единице:
det(E) = 1
- Определитель матрицы с двумя равными строками (столбцами) равен нулю.
- Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
- Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
- Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
- При транспонировании значение определителя матрицы не меняется:
det(A) = det(AT)
- Определитель обратной матрицы:
det(A-1) = det(A)-1
- Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
- Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
- Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
-
Общий множитель в строке (столбце) можно выносить за знак определителя:
1112…12122…2….·1·2…·….12… =
·1112…12122…2….12…….12… - Если квадратная матрица -того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в -той степени:
B = ·A => det(B) = ·det(A)
где A матрица ×, — число.
-
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:1112…12122…2….1 + 12 + 2… + ….12… =
1112…12122…2….12…….12… +
1112…12122…2….12…….12…
- Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
- Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)
Вычисление определителя матрицы при помощи теоремы Лапласа
Теорема Лапласа – это глубокое разложение определителя по элементам. При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков.
Напомним – минор – это определитель матрицы, который составлен методом вычёркивания
Приведём пример решения алгебраических дополнений по схеме:
Пример
Задача
Найти алгебраические дополнения элементов определителя:
Решение
Понятия алгебраического дополнения даёт возможность ещё одного способа определения определителя, который утверждается теоремой Лапласа (про распределение определителя):
Теорема
Определитель равняется сумме произведения элементов строк (столбца) на их алгебраические дополнения. Например,
. – это равенство проверяется непосредственно
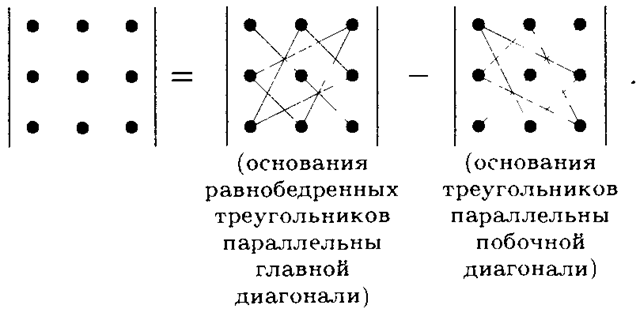
Заметно, как последнее выражение совпадает с выражением из правила треугольника (правила Саррюса). Давайте по теореме Лапласа разберём несколько примеров:
Пример
Задача
Вычислить определитель матрицы, разложив его за элементами третьего порядка:
Решение
Ответ
.
Постановка задачи
Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица, и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами данной работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры.
Вычисление определителя матрицы методом Гаусса.
Опишем суть этого метода. Матрица А с помощью элементарных преобразований приводится к такому виду, чтобы в первом столбце все элементы, кроме стали нулевыми (это сделать всегда возможно, если определитель матрицы А отличен от нуля). Эту процедуру опишем чуть позже, а сейчас поясним, для чего это делается. Нулевые элементы получаются для того, чтобы получить самое простое разложение определителя по элементам первого столбца. После такого преобразования матрицы А, учитывая восьмое свойство и , получим
где — минор (n-1)-ого порядка, получающийся из матрицы А вычеркиванием элементов ее первой строки и первого столбца.
С матрицей, которой соответствует минор , проделывается такая же процедура получения нулевых элементов в первом столбце. И так далее до окончательного вычисления определителя.
Теперь осталось ответить на вопрос: «Как получать нулевые элементы в первом столбце»?
Опишем алгоритм действий.
Если , то к элементам первой строки матрицы прибавляются соответствующие элементы k-ой строки, в которой . (Если все без исключения элементы первого столбца матрицы А нулевые, то ее определитель равен нулю по второму свойству и не нужен никакой метод Гаусса). После такого преобразования «новый» элемент будет отличен от нуля. Определитель «новой» матрицы будет равен определителю исходной матрицы в силу седьмого свойства.
Теперь мы имеем матрицу, у которой . При к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на . И так далее. В заключении к элементам n-ой строки прибавляем соответствующие элементы первой строки, умноженные на . Так будет получена преобразованная матрица А, все элементы первого столбца которой, кроме , будут нулевыми. Определитель полученной матрицы будет равен определителю исходной матрицы в силу седьмого свойства.
Разберем метод при решении примера, так будет понятнее.
Пример.
Вычислить определитель матрицы порядка 5 на 5 .
Решение.
Воспользуемся методом Гаусса. Преобразуем матрицу А так, чтобы все элементы ее первого столбца, кроме , стали нулевыми.
Так как изначально элемент , то прибавим к элементам первой строки матрицы соответствующие элементы, например, второй строки, так как :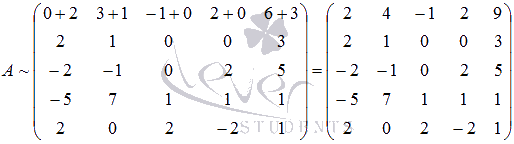
Знак « ~ » означает эквивалентность.
Теперь прибавляем к элементам второй строки соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на , и аналогично действуем вплоть до шестой строки: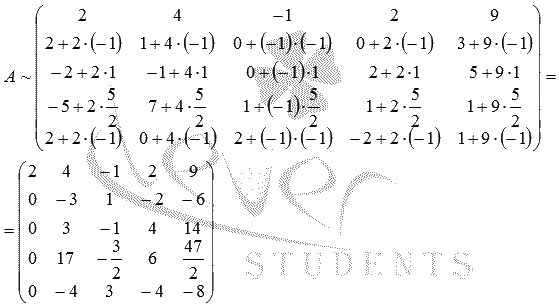
Получаем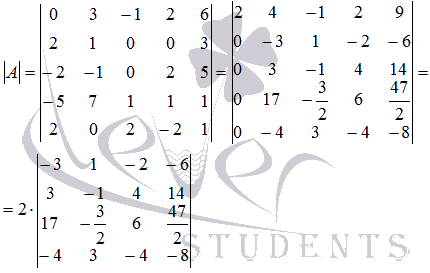
С матрицей проводим ту же процедуру получения нулевых элементов в первом столбце:
Следовательно,

Сейчас выполняем преобразования с матрицей :
Получаем
Матрица уже имеет необходимый вид, поэтому
Ответ:
.
Рассмотрим решение еще одного примера, но подробно описывать действия не будем. Это некоторый образец краткой записи вычисления определителя матрицы методом Гаусса.
Пример.
Вычислите определитель матрицы порядка 7 на 7.
Решение.

Следовательно,
Замечание.
На некотором этапе преобразования матрицы по методу Гаусса может возникнуть ситуация, когда все элементы нескольких последних строк матрицы станут нулевыми. Это будет говорить о равенстве определителя нулю.
Подведем итог.
Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:
- через сумму произведений сочетаний элементов матрицы;
- через разложение определителя по элементам строки или столбца матрицы;
- методом приведения матрицы к верхней треугольной (методом Гаусса).
Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.
Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.
При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.
Некогда разбираться?
Общая схема вычисления определителей
Как мы знаем, с ростом размерности матрицы $n$ количество слагаемых в определителе составляет $n!$ и быстро растёт. Всё-таки факториал — это вам не хрен собачий довольно быстро растущая функция.
Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка.
Готовы? Поехали!
Что такое минор матрицы
Пусть дана произвольная матрица $A=\left$. Заметьте: не обязательно квадратная. В отличие от определителей, миноры — это такие няшки, которые существуют не только в суровых квадратных матрицах. Выберем в этой матрице несколько (например, $k$) строк и столбцов, причём $1\le k\le m$ и $1\le k\le n$. Тогда:
Совершенно необязательно, чтобы выбранные строки и столбцы стояли рядом, как в рассмотренном примере. Главное, чтобы количество выбранных строк и столбцов было одинаковым (это и есть число $k$).
Есть и другое определение. Возможно, кому-то оно больше придётся по душе:
Как говорил мой кот, иногда лучше один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.
Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше.
Алгебраические дополнения
«Ну ok, и что дают нам эти миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.
Обозначаются дополнительные миноры с помощью «звёздочки»: $M_{k}^{*}$:
\
где операция $A\nabla {{M}_{k}}$ буквально означает «вычеркнуть из $A$ строки и столбцы, входящие в ${{M}_{k}}$». Эта операция не является общепринятой в математике — я её сам только что придумал для красоты повествования.:)
Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения.
Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример:
Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда.
Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте:
Теорема Лапласа
И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны.
Ладно, ладно: про $C_{n}^{k}$ — это я уже понтуюсь, в оригинальной теореме Лапласа ничего такого не было. Но комбинаторику никто не отменял, и буквально беглый взгляд на условие позволит вам самостоятельно убедиться, что слагаемых будет именно столько.:)
Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок.
Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы.
Разложение определителя по строке и столбцу
То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями.
Читайте и наслаждайтесь:
Из этого следствия можно сразу сформулировать несколько выводов:
- Эта схема одинаково хорошо работает как для строк, так и для столбцов. На самом деле чаще всего разложение будет идти именно по столбцам, нежели по строкам.
- Количество слагаемых в разложении всегда ровно $n$. Это существенно меньше $C_{n}^{k}$ и уж тем более $n!$.
- Вместо одного определителя $\left$ придётся считать несколько определителей размера на единицу меньше: $\left$.
Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:)
Что ж, попробуем посчитать одну такую задачку?
Миноры и алгебраические дополнения
Определитель -го порядка, получающийся вычеркиванием из
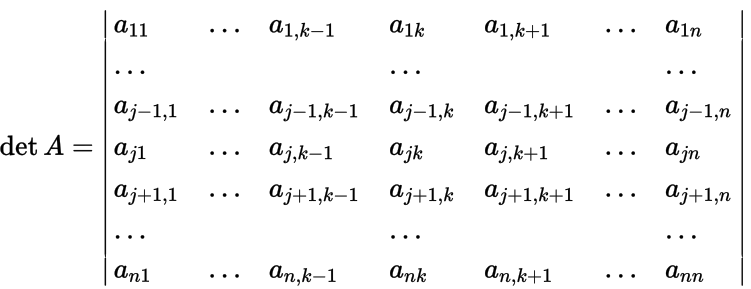
-й строки и -го столбца называется минором -го порядка этого определителя, соответствующим элементу . Будем обозначать его :

Величина
называется алгебраическим дополнением элемента в .
Пусть при и , и при и — две чисел от до .
В матрице выделим строк с номерами и столбцов с номерами . Элементы , стоящие в этих строках и столбцах, образуют определитель -го порядка:

Он называется минором порядка k матрицы .
Главным минором порядка квадратной матрицы называется определитель

т.е. определитель, образованный элементами первых строк и первых столбцов матрицы.
!
В современной и классической литературе имеются существенные различия в терминологии. Достаточно часто главным минором квадратной матрицы называют минор

составленный из элементов матрицы, стоящих в строках и столбцах с одинаковыми номерами. Минор же
рассматривается тогда как частный случай и специального названия в русском языке не имеет. В настоящем ресурсе я придерживаюсь версии определения главного минора, приведенной выше. Однако в двух разделах (
☞
ЗДЕСЬ ) мне придется иметь дело именно с минором
я буду называть его тогда ведущим минором.
Т
Теорема. Определитель матрицы равен сумме произведений элементов некоторого ряда (строки или столбца) определителя на их алгебраические дополнения. Иначе говоря, справедливы следующие формулы разложения определителя по -й строке (или по элементам -й строки):
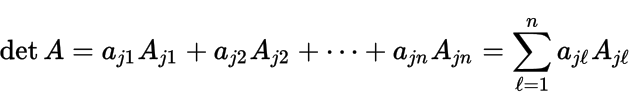
и разложения определителя по -му столбцу:

для любых .
Доказательство
☞
ЗДЕСЬ.
П
Пример. Разложение определителя третьего порядка по первому столбцу:

по второму столбцу:
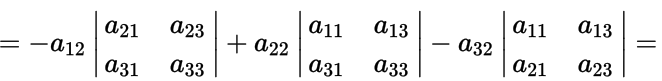
и по третьему столбцу:

П
Пример. Вычислить
разложив определитель по третьей строке.
Решение. В формуле берем :
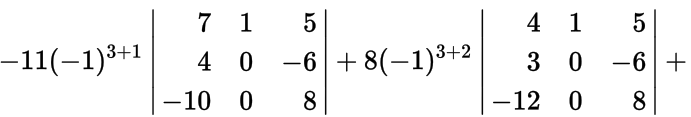
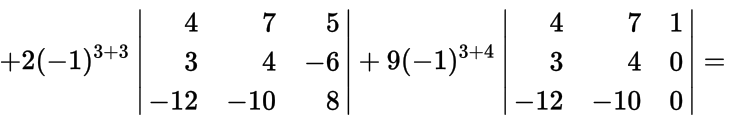
и используем формулу вычисления определителя третьего порядка:

Заметим, что тот же самый результат можно было бы получить, сэкономив на
вычислении определителей третьего порядка, если бы мы разложили исходный определитель по третьему столбцу:

Наличие нулевых элементов «облегчает жизнь» вычислителю…
!
А что делать, если среди элементов определителя нет нулевых? — Их надо «сделать».
Для этого в нашем распоряжении имеется такое средство, как преобразования строк или столбцов. В самом деле, на основании общего
6
определителя, к любой его строке можно прибавить любую другую строку, домноженную на произвольное число — определитель
от этого не изменится; аналогичное свойство справедливо и для столбцов. Но тогда мы можем упомянутые множители подбирать так, чтобы
добиться появления как можно большего количества нулей в отдельной строке (или столбце).
П
Пример. Вычислить
Решение. Будем добиваться появления нулей во втором столбце.
С этой целью прибавим вторую строку к третьей, четвертой и пятой, а
также вычтем, домножив предварительно на , из первой:

раскладываем по второму столбцу:

и вот уже порядок понизился. Вычитаем из третьего столбца первый:
теперь имеет смысл увеличить число нулевых элементов в третьем столбце —
вычитаем из четвертой строки первую:
Раскладываем по третьему столбцу:
Можно было бы применить теперь формулу разложения определителя третьего
порядка, но можно и продолжить упрощения — вычтем из третьей строки первую и вторую:
и разложим по третьей строке:

Систематическое развитие идеи, использованной при решении последнего примера, приводит к основному методу вычисления определителя — .
Следующий результат имеет исключительно теоретическое значение: используется для доказательства некоторых результатов.
Т
Теорема. Сумма произведений элементов -го ряда на алгебраические дополнения элементов -го ряда равна 0 если и равна
если :
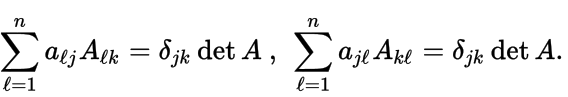
Здесь — .
Доказательство
☞
ЗДЕСЬ.
Применения.
Решение системы уравнений
можно получить, если первое уравнение умножить на b2, второе – на b1, а затем вычесть одно уравнение из другого. Проделав эти операции, мы получим
или, если
то
Такая запись решения с помощью определителей допускает обобщение на случай решения системы n линейных уравнений с n неизвестными; каждый определитель будет n-го порядка. Определителем системы линейных уравнений
будет
Заметим, что если D = 0, то уравнения либо несовместны, либо не являются независимыми. Поэтому предварительное вычисление определителя D позволяет проверить, разрешима ли система линейных уравнений.
Определитель оператора
рассматривается
☞
.
☞
ЗДЕСЬ.
Источники
. Нетто Е. . Mathesis. Одесса. 1912
. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948
. Turnbull H.W. The Theory of Determinants, Matrices and Invariants. Blackie & Sons Ltd. 1929
determinator (лат.) — определяющий.
И для матриц порядка выше первого!
Специфическое обозначение определителя матрицы с помощью вертикальных черт, ее ограничивающих, предложено .
minor (лат.) — меньший; minores — дети, молодежь.
principal minor (англ.); Hauptminor (Hauptunterdeterminante) (нем.).
В англоязычной литературе называется leading principal minor, в немецкоязычной — führenden Hauptminor
(Hauptunterdeterminante), т.е. что-то типа фюрерминор…
Обозначение не является общеупотребительным.
Иногда его называют равенством Сильвестра, но если рассматривать определитель как функцию его элементов, то это — именно тождество.
Методы вычисления определителей
Метод приведения к треугольному виду (метод Гаусса)
Напомним свойство
6
из : величина определителя не изменится если прибавить к любой его строке любую другую строку, умноженную на произвольную константу. Этот факт можно использовать для того, чтобы «сделать» в определителе побольше элементов равных нулю, т.к. содержащие эти элементы слагаемые выпадут из .
Еще одно элементарное свойство —
2
, утверждает, что перестановка строк изменит знак определителя, но не изменит его абсолютную величину. Пользуясь этими двумя преобразованиями, можем поставить целью привести определитель к треугольному виду, т.е. к виду

Тогда, на основании следствия к , величина исходного определителя с точностью до знака будет совпадать с произведением диагональных элементов:
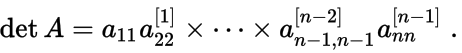
Формализовать приведение определителя к треугольному виду возможно с помощью используюшегося при решении систем линейных уравнений . Так, первый шаг преобразования определителя

будет состоять в «обнулении» элементов первого столбца: из второй строки вычитается первая, домноженная на , из третьей строки — первая, домноженная на и т.д. Все эти операции не изменяют величины определителя, но преобразуют его к виду

(при условии ). Теперь можно и свести задачу к вычислению определителя порядка .
П
Пример. Вычислить
методом Гаусса.
Решение. Вычитаем первую строку, умноженную на соответствующие числа, из остальных строк, добиваясь появления нулей в первом столбце:

Выносим общий множитель элементов последней строки:

Поскольку элемент, стоящий во второй строке и втором столбце нулевой, то поменяем местами вторую и пятую строки, при этом знак определителя изменится:

Теперь с помощью второй строки обращаем в нуль элементы второго столбца:

Чтобы избежать появления дробных элементов, поменяем местами третью и четвертую строки, определитель при этом снова поменяет знак:


?
Вычислить .
И
Биографические заметки о Гауссе
☞
.
Вычисление целочисленного определителя
§
Материал этого пункта предполагает (хотя бы беглое) знакомство с разделом .
П
Пример. Верно ли равенство

Решение. Фактическое вычисление подобного определителя —
каким бы мы не воспользовались —
задача довольно трудоемкая. Однако
вопрос ставится не о фактическом значении, а о равенстве его нулю.
Это обстоятельство может упростить вычисления. Обозначим неизвестное
значение определителя через ; очевидно это число целое. Если ,
то и его остаток при делении на любое число тоже должен
быть равным нулю. Если же хоть для
одного выполнится условие , то и .
Вычисление определителя фактически . Если же мы ставим задачу определения остатка
от деления этого выражения на , то имеет смысл
сразу же «сократить» каждый элемент определителя до его остатка от деления
на .
Возьмем сначала , т.е. от каждого элемента определителя оставляем
только последнюю цифру:

Итак, полученный ответ является необходимым, но не достаточным условием
равенства определителя нулю. Сделаем еще одну проверку: возьмем .
Ответ. Равенство неверно.
Понятно, что если бы определитель был равен нулю, то каждое вычисление
по модулю только «увеличивало бы достоверность» этого события.
Можно ли на основе серии модулярных вычислений установить истинное значение
определителя?
☞
.
§
А складировать встретившиеся на моем пути целочисленные определители буду
☞
ЗДЕСЬ.
Часто встречающиеся определители
Вандермонда

Доказательство
☞
.
=>
тогда и только тогда, когда среди чисел имеются одинаковые.
§
☞
ИНТЕРПОЛЯЦИЯ.
Частным случаем определителя Вандермонда является определитель матрицы дискретного преобразования Фурье:

— . Основываясь на свойстве , матрицу часто записывают в эквивалентном виде

=>
при — четном, при — нечетном.
Доказательство
☞
ЗДЕСЬ.
Ганкеля
или определитель :

Элементы  — образующие ганкелевого определителя.
— образующие ганкелевого определителя.
§
☞
☞
;
☞
;
☞
.
П
Пример. При равен
П
Пример. При (определитель Гильберта) равен
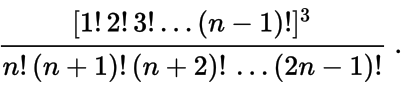
§
Вывод формулы
☞
ЗДЕСЬ;
☞
.
Грама
Пусть в векторном пространстве определено . Определителем Грама (или грамианом) системы векторов называется

Т
Теорема. тогда и только тогда, когда система векторов .
§
☞
ЗДЕСЬ
или определитель циклической матрицы

где  , а
, а
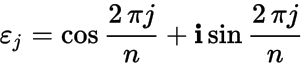
— .
Доказательство
☞
ЗДЕСЬ.
?
Найти явное выражение для циркулянта

Результант
Для полиномов  и
и  рассмотрим матрицу порядка
рассмотрим матрицу порядка

(элементы выше и , и ниже и все равны нулю). Выражение
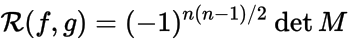
называется результантом (в форме Сильвестра) полиномов и .
Т
Теорема. Если — корни полинома , а — корни полинома , то

=>

=>
тогда и только тогда, когда полиномы и имеют общий корень.
§
☞
ЗДЕСЬ
Дискриминант
полинома  может быть определен через этого полинома и его производной:
может быть определен через этого полинома и его производной:

Дискриминант можно представить в виде определителя порядка :

Т
Теорема. Если — корни полинома , то
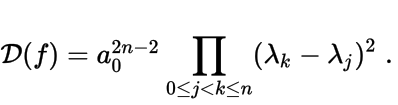
=>
тогда и только тогда, когда имеет .
§
☞
ЗДЕСЬ
Континуант
определяется как определитель :

и фактически является полиномом от — этот полином называется .
§
Континуант является частным случаем .
Т
Теорема. Имеет место рекуррентная формула
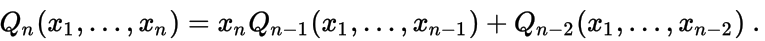
=>
Континуант равен сумме произведения и всевозможных произведений, получающихся из него вычеркиванием пар соседних множителей
(и добавлением в случае четного ).
П
Пример.

?
Сколько слагаемых содержится в полном разложении континуанта?
Подсказка
☞
Т
Теорема. Имеет место тождество

Доказательство следует из .
Якобиан
Якобианом или определителем Якоби или функциональным определителем системы из функций  по переменным
по переменным
называется определитель, составленный из частных производных:

Т
Якобиан тождественно равен нулю в некоторой области :
при
тогда и только тогда, когда между функциями имеется функциональная зависимость в , т.е. существует функция отличная от тождественного нуля, такая, что
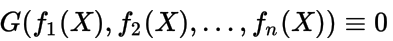 при
при
§
☞
ЗДЕСЬ
Гессиан
Гессианом или определителем Гессе функции называется якобиан ее частных производных, т.е. определитель

состоящий из частных производных второго порядка функции .
Вронскиан
системы функций — это определитель

Т
Теорема. Аналитические на интервале функции на тогда и только тогда, когда  на .
на .
§
☞
ЗДЕСЬ
Заключение
Итак, определитель квадратной матрицы – это число, полученное при помощи заданных чисел, расположенных в виде квадратной таблицы,которое вычисляется по рассмотренным выше формулам. Мы рассмотрели три основных способа вычисления определителя:
- через сумму двух произведений сочетаний элементов квадратной матрицы;
- по правилу разложения определителя по элементам строк (столбцов) квадратной матрицы;
- по методу Гаусса, когда матрицу нужно привести к треугольному виду.
Также были рассмотрены формулы для решения матрицы второго, третьего и высших порядков.
Мы разобрали 10 свойств определителя матриц, благодаря которым можно быстрее и легче найти определитель матрицы.
Удобно решать матрицу третьего порядка методом Гаусса, где нужно выполнить элементарные преобразования матрицы и привести её к ступенчатому виду. Определитель матрицы равняется произведению элементов, которые стоят на главной диагонали.
Полезная литература




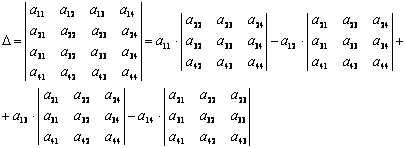


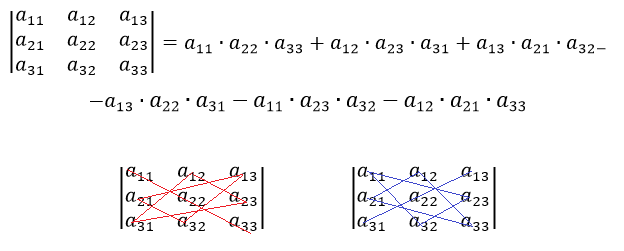
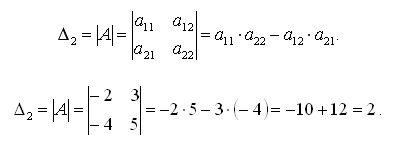
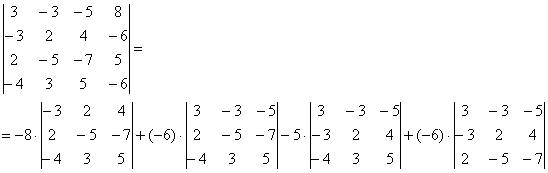

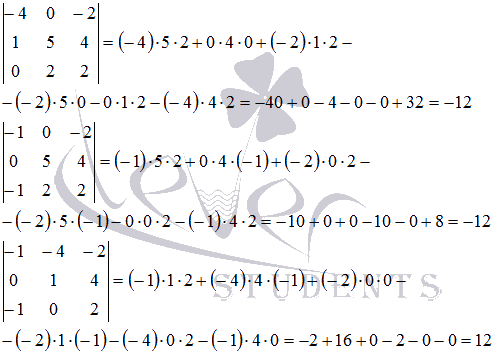
![Algebra2:dets [vf]](https://rusinfo.info/wp-content/uploads/0/f/1/0f180b20fcdfb41ef0cc70bc6b855793.png)



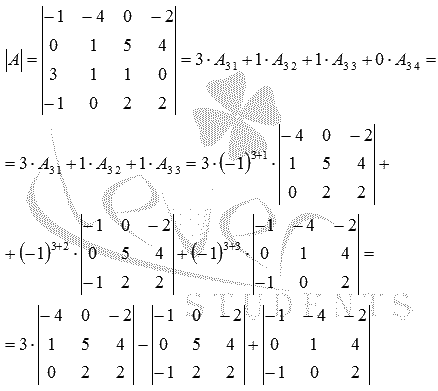
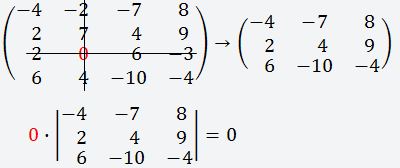
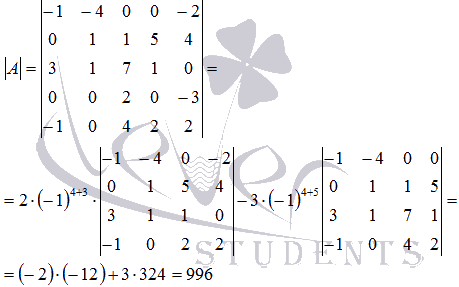
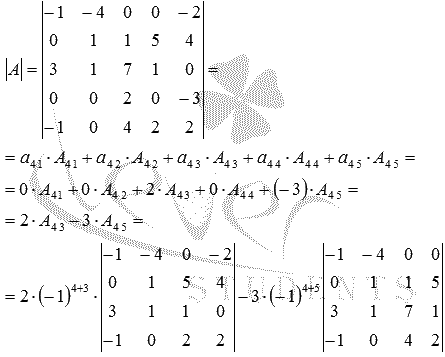

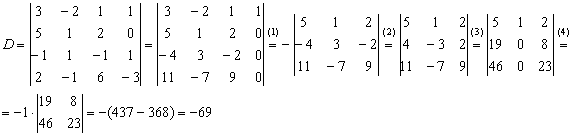



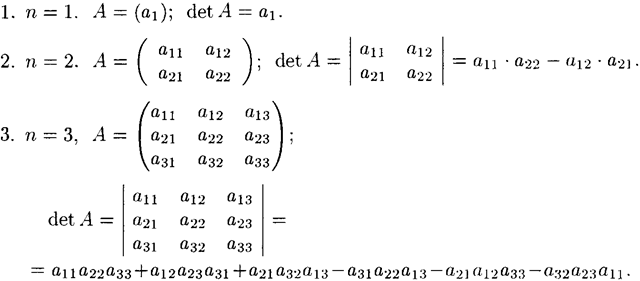




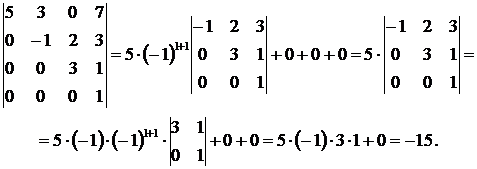


![Algebra2:dets [vf]](https://rusinfo.info/wp-content/uploads/d/f/6/df66ff57fc1c9266372c2341d85bb5aa.jpg)