Примечания
- // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если E→{\displaystyle {\vec {E}}} одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия E→{\displaystyle {\vec {E}}} в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле E→{\displaystyle {\vec {E}}} — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
- Хотя исторически многие из них были открыты раньше.
§ 5. Проводники в электрическом поле
Физический смысл изучения поля поверхностных зарядов коренится в том обстоятельстве, что в случае электростатического равновесия заряды проводников сосредоточиваются в весьма тонком поверхностном слое, который в громадном большинстве случаев можно с достаточной точностью считать бесконечно тонким. Ведь и непосредственно ясно, что если сообщить металлическому телу, например, отрицательный заряд (избыток электронов), то благодаря взаимному отталкиванию элементов этого заряда (электронов) они сосредоточатся на его поверхности. Строгое же доказательство этого утверждения можно дать на основании того факта, что в случае электростатического равновесия электрическое поле внутри проводника равно нулю.
Действительно, проводник есть тело, отличающееся следующим свойством: если в какой-либо точке внутри проводника напряженность электрического поля Е отлична от нуля, то в проводнике возникает электрический ток, т. е. движение зарядов. Это свойство можно рассматривать как определение термина «проводник электричества».
С точки зрения электронной теории важнейшего класса проводников — металлов — это свойство объясняется тем, что если металл находится в твердом (или жидком) состоянии, то часть электронов, входящих в состав его атомов, отщепляется от этих атомов. Оставшиеся после отщепления этих «свободных» электронов положительные ионы металла образуют его твердый скелет (кристаллическую решетку), в промежутках же между ионами находятся «свободные» электроны в форме своего рода «электронного газа». Сколь угодно слабое внешнее электрическое поле вызывает движение этих «свободных» электронов в направлении действующих на них сил, т. е. вызывает электрический ток. Ток течет до тех пор, пока напряженность поля внутри проводника не станет равной нулю, т. е. пока поле зарядов, перераспределившихся по объему проводника, не скомпенсирует внешнего поля.
Так как электрический вектор внутри проводника равен нулю, то равен нулю и поток этого вектора через любую замкнутую поверхность, расположенную внутри проводника. Стало быть, по теореме Гаусса, равен нулю и заряд, расположенный внутри всякой такой поверхности. А это и значит, что в случае электростатического равновесия зарядов внутри проводника нет (вернее, что положительные и отрицательные заряды внутри него взаимно нейтрализуются) и что все заряды расположены на его поверхности.
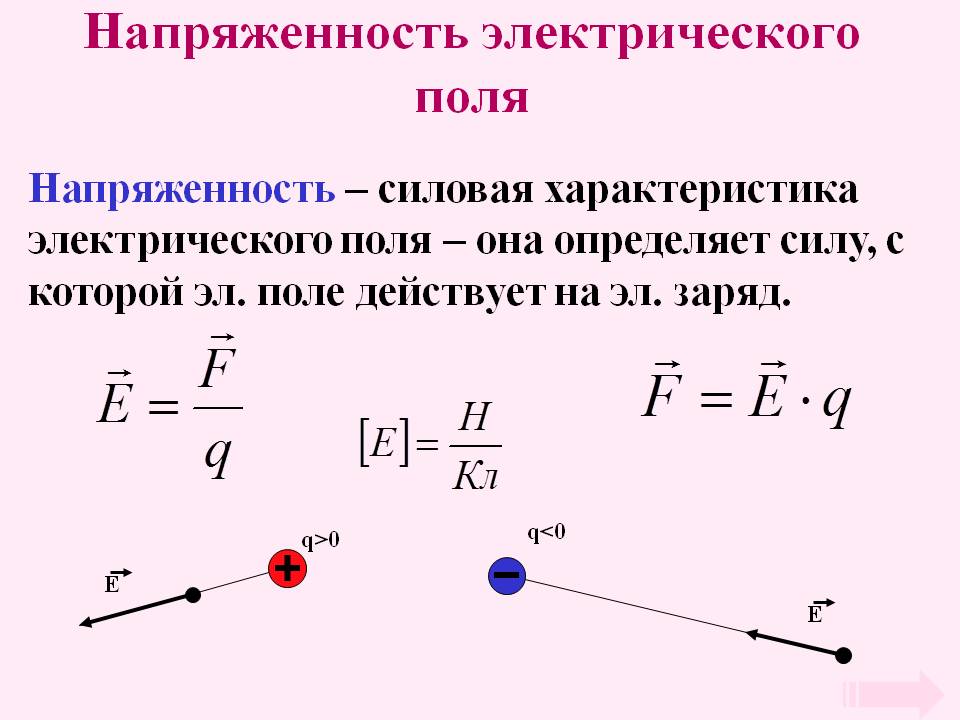
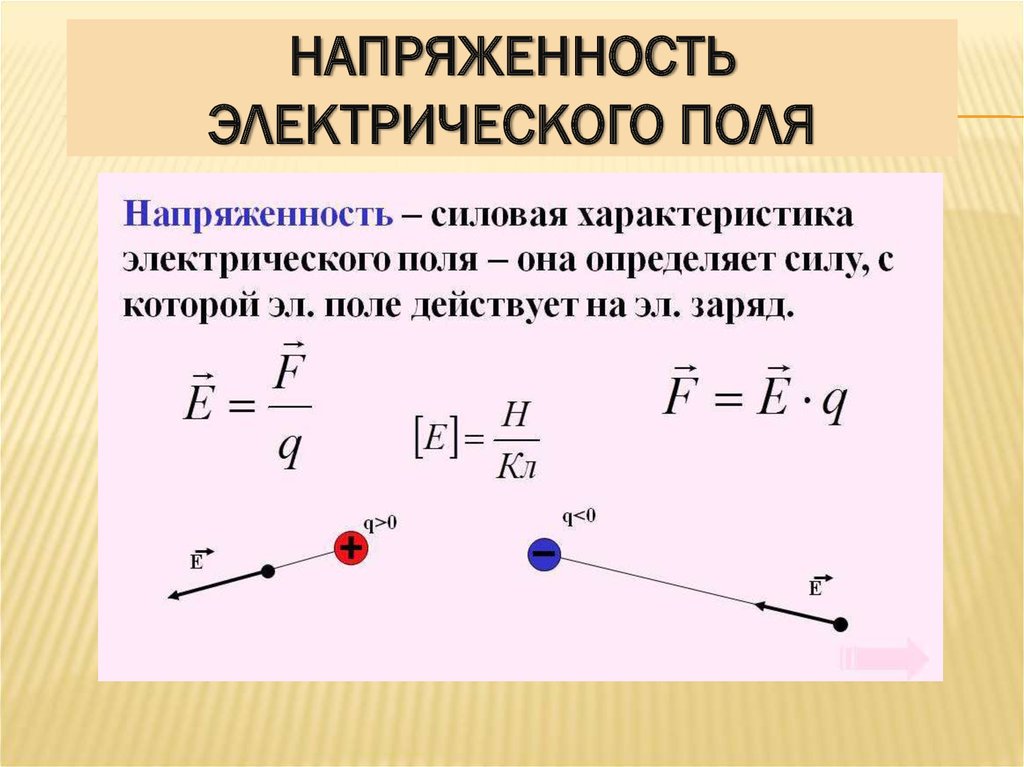
Как направлен вектор электрического поля
Вектор поля надо направить в сторону от положительного заряда и в обратном направлении – к отрицательному. Это определение справедливо для одной точки. Так как идеальные условия отсутствуют, в реальной ситуации приходится учитывать взаимодействие зарядов и соответствующее образование силовых линий.
 Силовые линии
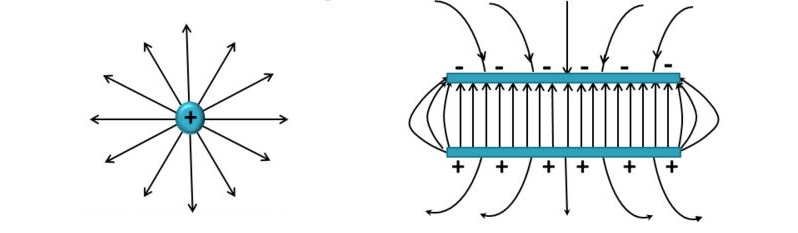
Силовые линии
Поле не является однородным, что демонстрируют с помощью разных расстояний между отдельными линиями. В примере с пластинами близкое расположение параллельных проводников позволяет обеспечить одинаковую напряженность в рабочей зоне. Все силовые линии бесконечные. Они начинаются на положительном заряде и заканчиваются на отрицательном. Таким образом, направление вектора напряженности будет всегда в сторону уменьшения потенциала.
Взаимодействие зарядов. Два вида зарядов
Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.
Обозначение – \( q \), единица измерения в СИ – кулон (Кл).
Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10-19 Кл), наименьший положительный заряд (1,6·10-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.
Величина заряда тела будет равна
где \( N \) — число избыточных или недостающих электронов; \( e \) — элементарный заряд, равный 1,6·10-19 Кл.
Важно! Частица может не иметь заряда, но заряд без частицы не существует. Электрические заряды взаимодействуют:
Электрические заряды взаимодействуют:
заряды одного знака отталкиваются:
заряды противоположных знаков притягиваются:
Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.
Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.
Потенциал электрического поля. Разность потенциалов
Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.
Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).
Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.
Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:
Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).
Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.
Важно! Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:
Важно! Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки
В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность
В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:
Для наглядного представления электрического поля используют эквипотенциальные поверхности.
Важно! Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю
Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.
Свойства эквипотенциальных поверхностей
- Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
- Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.
Разность потенциалов и напряженность связаны формулой:
Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:
Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.
Важно! Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил
Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.
Алгоритм решения таких задач:
- установить характер и особенности электростатических взаимодействий объектов системы;
- ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
- записать законы сохранения и движения для объектов;
- выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
- составить систему уравнений и решить ее относительно искомой величины;
- проверить решение.
Постоянный электрический ток
Электрический ток – направленное движение свободных носителей энергии в веществе или внутри вакуума. Этот показатель появляется при соблюдении главных условий:
- Есть источник энергии.
- Замкнутость пути, который используется для перемещения.
I – буква, которую применяют для обозначения силы тока.
 Пример задачи с напряжённостью
Пример задачи с напряжённостью
Важно. Единица измерения – Амперы
Величина тока зависит от количества электричества или разрядов, которые проходят через поперечное сечение у проводника в единицу времени.
Когда речь о постоянном токе – предполагается, что с течением времени не меняются его направление, основная величина.
 Вектор
Вектор
Амперметр – устройство, применяемое для измерения силы тока. Его подключение к цепи – последовательное. Показатель важен, поскольку от него зависят и сила воздействия и другие подобные параметры. На практике часто встречаются ситуации, когда сила тока заменяется плотностью. В данном случае единица измерения – Ампер на метр квадратный. Площадь сечения проводов выражается в мм2. И плотность тока предполагает опору на эту характеристику.
Электрическое поле можно назвать реально существующим явлением, как и любые предметы. Поле и вещества относят к основным формам существования материи. Способность действовать с силой на заряды – главное свойство. Его используют, чтобы обнаруживать, измерять явления. Ещё одна характеристика – распространение со скоростью света
Это тоже важно для тех, кто занимается изучением подобных факторов
Примечания
- // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если E→{\displaystyle {\vec {E}}} одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия E→{\displaystyle {\vec {E}}} в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле E→{\displaystyle {\vec {E}}} — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
- Хотя исторически многие из них были открыты раньше.
«Материальные уравнения»
Для решения многих практических задач вполне достаточна ограниченная точность. С помощью «материальных» уравнений выполняют расчеты различных электрических цепей.
Уместный пример – закон Ома. Он был создан в ходе измерения электрических параметров. В начальном виде формула (Х=П/L+B) состояла из следующих компонентов:
- Х – показания измерительного устройства (гальванометра), включенного в разрыв электрической цепи;
- П – параметры источника питания, заставляющие стрелку прибора отклоняться на определенный угол;
- L – длина соединительных проводов;
- B – общие свойства установки.
Несложно догадаться, что в современном представлении это известный закон, показывающий взаимное влияние основных параметров полной электрической цепи:
I = E/R+r,
где:
- I – ток;
- E – ЭДС (напряжение);
- R и r – сопротивление подключенных компонентов и самого источника питания, соответственно.
Силовые линии
Коль скоро электрическое поле является векторным, его можно изображать в различных точках стрелками, как это сделано на рис. 22.13. Направления векторов Еа, Еb, Ес совпадали бы с направлениями показанных на этом рисунке сил и лишь длина их была бы уже иной в результате деления на q. Отношение длин векторов Еа, Еb, Ес сохранится прежним, так как мы делим на один и тот же заряд. Однако изображать электрическое поле таким образом неудобно, поскольку при большом числе точек весь рисунок будет испещрен стрелками. Поэтому пользуются другим способом изображения поля-методом силовых линий.
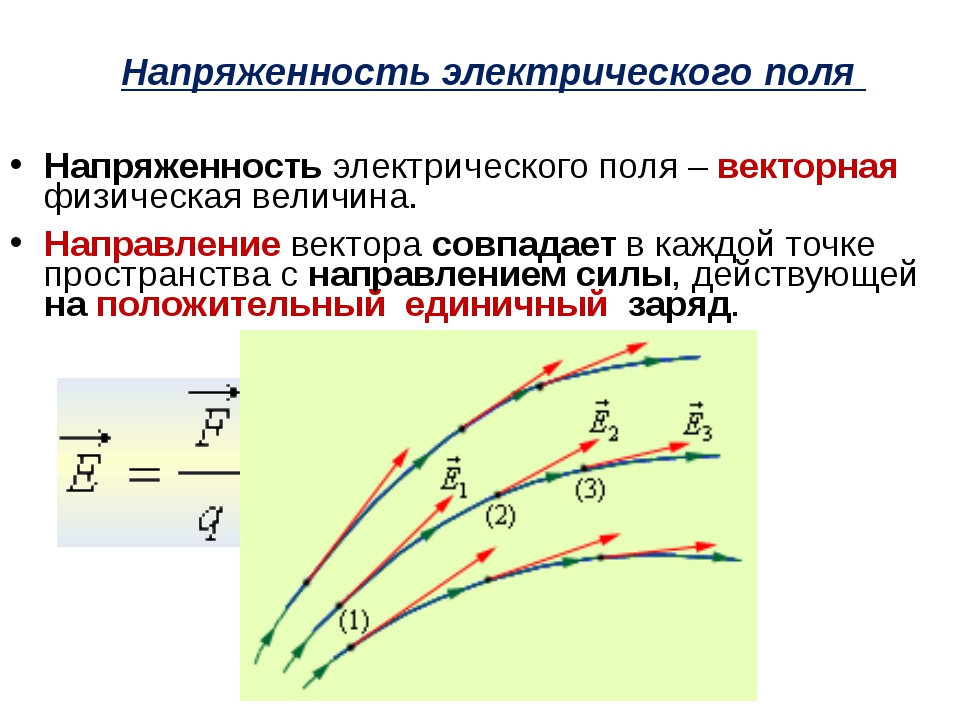
Для наглядного представления электрического поля его изображают семейством линий, указывающих направление напряженности поля в каждой точке пространства.
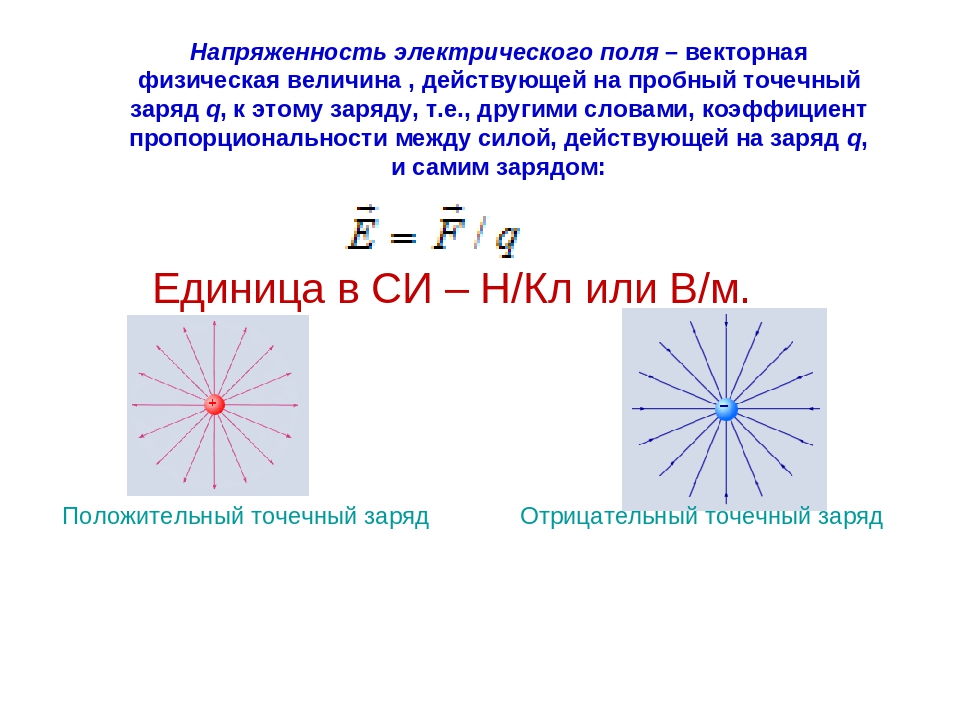
Эти так называемые силовые линии проводятся так, чтобы указывать направление силы, действующей в данном поле на положительный пробный заряд. Силовые линии точечного положительного заряда показаны на рис. 22.20, а, отрицательного — на рис. 22.20,6.
В первом случае линии радиально расходятся от заряда, во втором они радиально сходятся к заряду. Именно в таком направлении будут
действовать силы на положительный пробный заряд. Конечно, силовые линии можно нанести и в промежутках между изображенными на рисунке
Но мы условимся наносить силовые линии с таким расчетом, чтобы число линий, исходящих от положительного заряда или заканчивающихся на отрицательном заряде, было пропорционально величине этого заряда.
Обратим внимание на то, что вблизи заряда, где сила максимальна, линии расположены более тесно. Это общее свойство силовых линий: чем теснее расположены силовые линии, тем сильнее электрическое поле в этой области
Вообще говоря, можно всегда изображать силовые линии таким образом, чтобы число линий, пересекающих единичную площадку,
перпендикулярную направлению поля Е, было пропорционально напряженности электрического поля. Например, для уединенного точечного заряда (рис. 22.20) напряженность электрического поля убывает как 1/r 2; так же будет уменьшаться с расстоянием и число равномерно распределенных силовых линий, пересекающих единичную площадку: ведь общее число силовых линий остается
постоянным, а площадь поверхности, через которую они проходят, растет как 4πr 2 (поверхность сферы радиусом
г). Соответственно число силовых линий на единицу площади пропорционально 1/r 2.
На рис. 22.21, а показаны силовые линии поля, создаваемого двумя зарядами противоположных знаков. Здесь силовые линии искривлены и направлены от положительного заряда к отрицательному. Поле в любой точке направлено по касательной к силовой линии, как показано
стрелкой в точке Р.
На рис. 22.21,6 и в показаны силовые линии электрического поля двух положительных зарядов и поля между двумя параллельными
противоположно заряженными пластинами. Заметим, что силовые линии поля между пластинами параллельны и расположены на равном расстоянии друг от друга, исключая область вблизи краев.
Таким образом, в центральной области напряженность электрического поля во всех точках одинакова, и мы можем написать:Е = const (между близко расположенными параллельными пластинами).
Хотя вблизи краев это не так (силовые линии изгибаются), часто этим можно пренебречь, особенно если расстояние между пластинами мало по сравнению с их размерами. .
Итак, силовые линии обладают следующими свойствами:
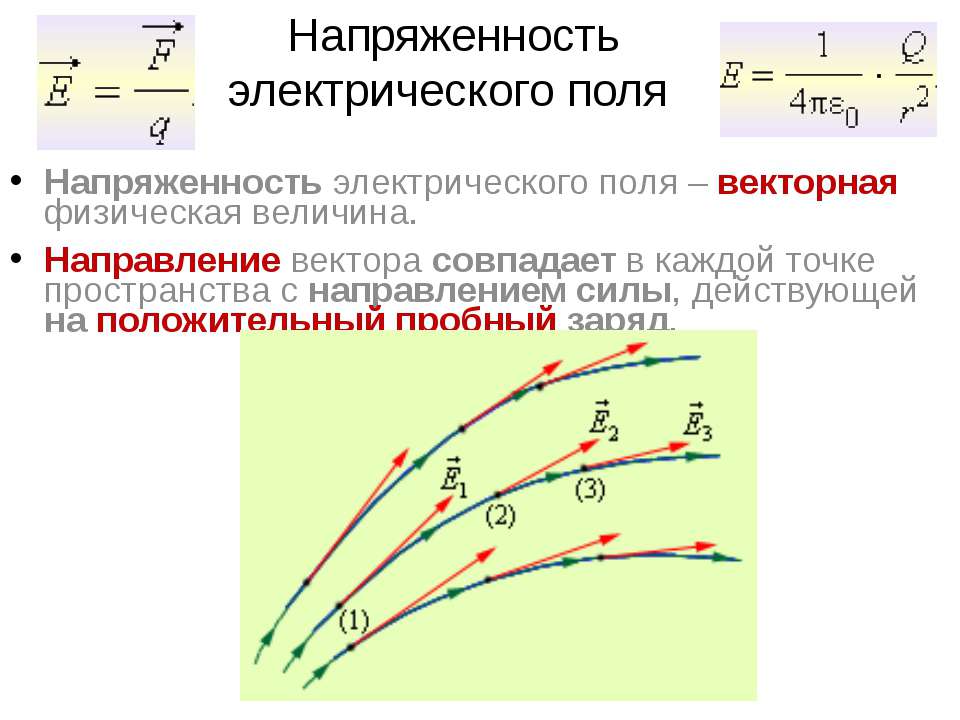
1. Силовые линии указывают направление напряженности электрического поля: в любой точке напряженность поля направлена по касательной к силовой линии.
2. Силовые линии проводятся так, чтобы напряженность электрического поля Е была пропорциональна числу линий, проходящих через единичную площадку, перпендикулярную линиям.
3. Силовые линии начинаются только на положительных зарядах и заканчиваются только на отрицательных зарядах; число линий, выходящих из заряда или входящих в него, пропорционально величине заряда.
Можно также сказать, что силовая линия электрического поля — это траектория, по которой следовал бы помещенный в поле малый пробный заряд. (Строго говоря, это верно лишь в том случае, если пробный заряд не обладает инерцией или движется медленно, например вследствие
трения.)
Силовые линии никогда не пересекаются. (Если бы они пересекались, это означало бы, что в одной и той же точке напряженность электрического поля имеет два различных направления, что лишено смысла.)
Сила порождаемая электрическими зарядами
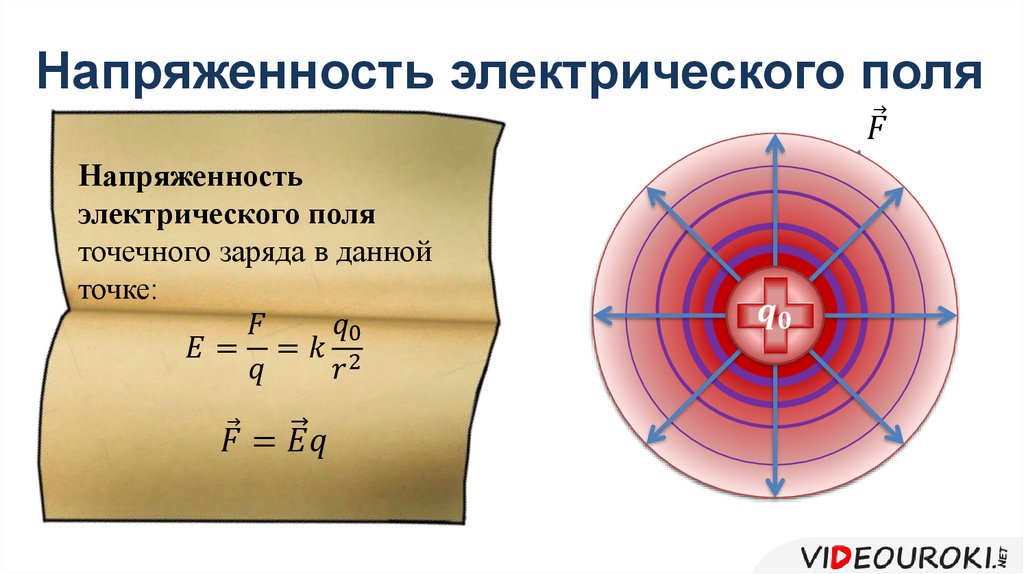
Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.
Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.
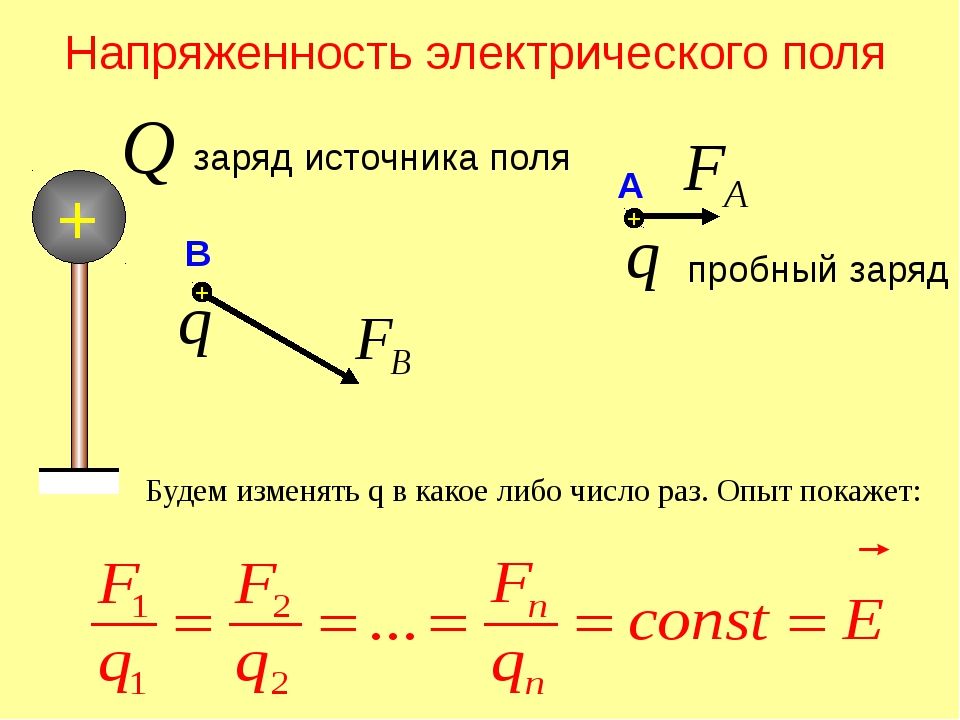
Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы. Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля. В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.
Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях. Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля. Пробный заряд имеет некоторое количество заряда и обозначается символом q.
При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы — или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.
Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как
Стандартные метрические единицы измерения напряженности электрического поля возникают из его определения. Таким образом напряженность электрического поля определяется как сила равная 1 Ньютону (Н) деленному на 1 Кулон (Кл). Напряженность электрического поля измеряется в Ньютон/Кулон или иначе Н/Кл. В системе СИ также измеряется в Вольт/метр. Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.
В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).
Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет. Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q — скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза. Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз. Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.
Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.
Более подробно о формуле напряженности электрического поля
Выше мы коснулись определения напряженности электрического поля в том, как она измеряется. Теперь мы попробуем исследовать более развернутое уравнение с переменными, чтобы яснее представить саму суть вычисления и измерения напряженности электрического поля. Из уравнения мы сможем увидеть, что именно влияет, а что нет. Для этого нам прежде всего потребуется вернутся к уравнению Закона Кулона.
Закон Кулона утверждает, что электрическая сила F между двумя зарядами прямо пропорциональна произведению количества этих зарядов и обратно пропорциональна квадрату расстояния между их центрами.
Если внести в уравнение Закона Кулона два наших заряда Q (источник) и q (пробный заряд), тогда мы получим следующую запись:
Если выражение для электрической силы F, как она определяется Законом Кулона подставить в уравнение для напряженности электрического поля E, которое приведено выше, тогда мы получим следующее уравнение:
Обратите внимание, что пробный заряд q был сокращен, то есть убран как в числителе так и в знаменателе. Новая формула для напряженности электрического поля E выражает напряженность поля в терминах двух переменных, которые влияют на нее
Напряженность электрического поля зависит от количества исходного заряда Q и от расстоянии от этого заряда d до точки пространства, то есть геометрического места, в котором и определяется значение напряженности. Таким образом у нас появилась возможность характеризовать электрическое поле через его напряженность.
Электростатика
Этот раздел электродинамики описывает частный случай, когда заряженные тела находятся в статичном состоянии. Такая ситуация значительно упрощает расчеты. Для практического примера можно создать электростатический конденсатор.
Устанавливают две плоскости одинаковой размерности параллельно на небольшом расстоянии, разделяют слоем диэлектрика. Если создать разницу потенциалов, между поверхностями образуется поле. В такой конструкции накапливается электрический заряд. Какой будет емкость, можно узнать с помощью этой формулы:
C=Q/ (ϕ1-ϕ2)=Q/U=e*S/d,
где
- e – проницаемость диэлектрика;
- e0 – электрическая постоянная (8,85*10-12 Ф/м);
- S – площадь пластин;
- D – расстояние между ними.
 Конденсатор
Конденсатор
Чтобы зарядить конденсатор до нужной емкости, надо затратить энергию W=(e*e0*E2/2)*S*D. На рисунке показано, как изменять рабочие параметры сборки при последовательном и параллельном соединении модулей.
Теорема Гаусса
Эта теорема определяет пропорциональность потока вектора напряженности электрического поля (Ф) заряду (Q), который заключен в произвольную поверхность замкнутого типа:
Ф=4π*Q.
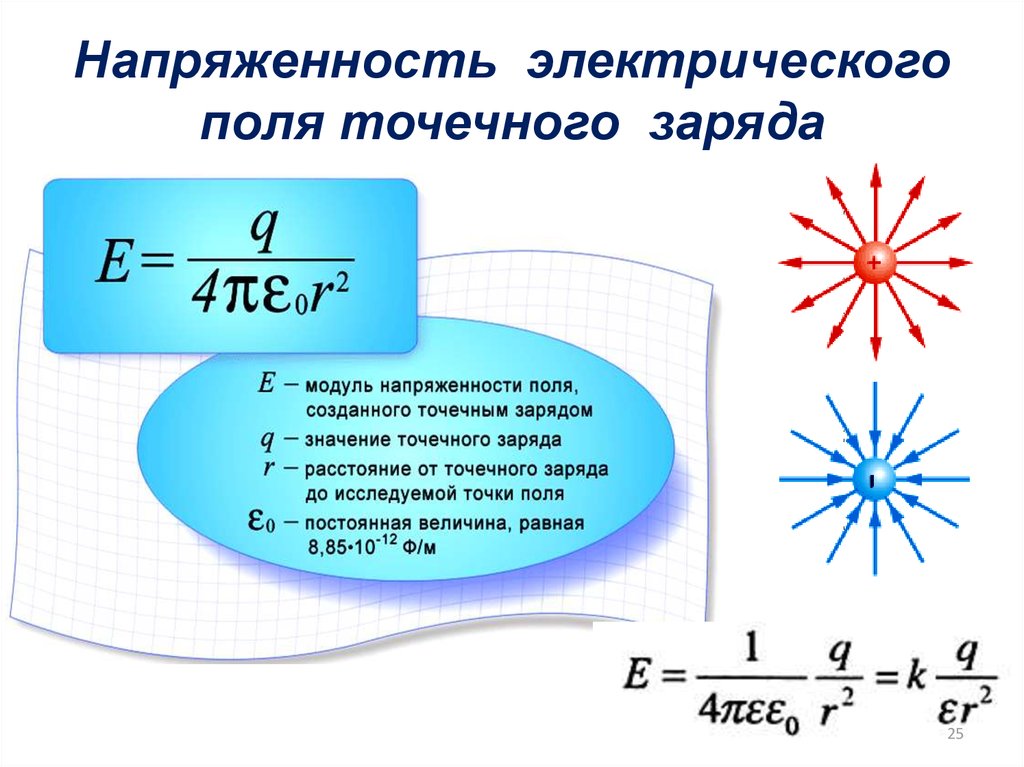
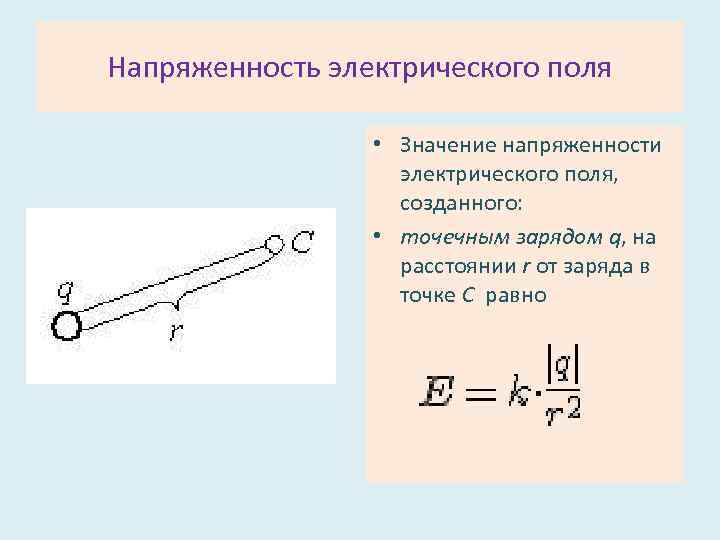
Напряжённость электрического поля точечного заряда
В этом случае можно пользоваться рассмотренным выше законом Кулона. В следующих разделах представлены формулы для вычисления в разных системах единиц.
В единицах СИ
В этой системе базовой выбрана сила тока, поэтому кулон является производной величиной.
Основная формула:
F=k*(q1*q2/r122).
Здесь коэффициент k=1/(4π*e0).
Для системы СГС
Здесь, как и в предыдущем примере, выбран единичный заряд – «точка». Основные правила характеризуют физические процессы аналогично. Разница лишь в постоянных величинах. В данном случае коэффициент k обратно пропорционален диэлектрической проницаемости (е) среды.
В этом варианте для получения результата надо сложить вектора каждого заряда:
Еобщ=Е1+Е2+…+En.
Чтобы обеспечить непрерывность линии напряженности, берут интеграл соответствующей области. Построить распределение силовых линий можно с помощью расчета перемещения вектора по всем точкам.
С точки зрения термодинамики
Напряженность выступает одним из основных и ключевых характеристик в классической электродинамике. Ее значение, а также данные электрического заряда и магнитной индукции представляются основными характеристиками, зная которые можно определить параметры протекания практически всех электродинамических процессов. Она присутствуют и выполняет важную роль в таких фундаментальных понятиях, как формула силы Лоренца и уравнения Максвелла.
Где:
F-сила Лоуренца;
- q – заряд;
- B – вектор магнитной индукции;
- С – скорость света в вакууме;
- j – плотность магнитного тока;
- μ0 – магнитная постоянная = 1,25663706*10-6;
- ε– электрическая постоянная, равная 8,85418781762039*10-12
Наряду со значением магнитной индукцией данный параметр является основной характеристикой электромагнитного поля, излучаемого зарядом
Исходя из этого, с точки зрения термодинамики напряженность – значительно более важное значение, чем сила тока или другие показатели
Данные законы выступают фундаментальными, на них строится вся термодинамика. Следует отметить, что закон Ампера и другие более ранние формулы являются приближенными или описывают частные случаи. Законы Максвелла и Лоренца универсальны.