Проблемы в множителе Math
В первом выводе Кейнса доход (Y) рассматривается как независимая переменная или причина, которая ведет к другим изменениям в экономике; после введения понятия k, но инвестиции (I) и множитель (k) были внезапно независимыми переменными. Доход стал зависимой переменной или эффектом.
Множитель Кейнса изменил причину и эффект после введения k. Хотя математически это верно, это разворот только продемонстрировал необходимые учетные отношения в уравнении Кейнса, а не какую-либо значимую причинную связь.
Для аналогии рассмотрим уравнение для преобразования Цельсия в градусы Фаренгейта: F = 32 + 1. 8C. При этом увеличение на 10 градусов Цельсия означает увеличение на 18 градусов по Фаренгейту.Это можно выразить математически как dF / dC = k, где k — мультипликатор Цельсия. (Математически, это идентично кейнсианскому множителю.)
Было бы нецелесообразно утверждать, что повышение по Цельсию на 10 градусов приводит к увеличению Фаренгейта на 18 градусов. Эти два могут быть математически связаны в фиксированном уравнении, но нет разумной причинно-следственной связи. То же самое касается кейнсианских множителей.
Действительно, вывод кейнсианского множителя можно записать dY / dC = 1 / b. При MPC = 0. 8 изменение в доходе составляет всего лишь 1,25 раза больше изменений в новых расходах, а не в пять раз.
Умножение многозначного числа на многозначное
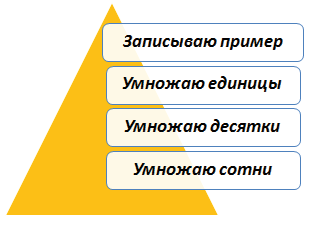
Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.
Три произведения

называются частными произведениями.
Полное произведение 3029 × 429 равно сумме трех частных:
3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.
Найдем величины этих трех частных произведений.
-
Умножая 3029 на 9, находим:
3029 × 9 27261 первое частное произведение
-
Умножая 3029 на 20, находим:
3029 × 20 60580 второе частное произведение
-
Умножая 3026 на 400, находим:
3029 × 400 1211600 третье частно произведение
Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.
Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.
Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.
Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.
Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,
-
нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.
-
Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.
-
Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.
-
Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.
Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.
Пример. Найти произведение 342 на 2700.
Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.
Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35
Приписывая к 945 пять нулей, получаем искомое произведение:
2700 × 35000 = 94500000.
Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).
Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.
В нашем произведении может содержаться или 7 или 6 цифр.
Определение умножения
Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.
Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.
Умножение есть сложение равных слагаемых.
Данные в умножении называются множимым и множителем, а искомое — произведением.
В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.
Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.
Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.
Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.
Множимое и множитель вместе называются производителями.
При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.
Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.
Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать
7 + 7 + 7
пишут при помощи знака умножения короче:
7 × 3 или 7 · 3
Умножение есть сокращенное сложение равных слагаемых.
Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).
Связь между данными и искомым числом выражается в умножении
письменно:
7 × 3 = 21 или 7 · 3 = 21
словесно:
семь, умноженное на три, составляет 21.
Чтобы составить произведение 21, нужно 7 повторить три раза
21 = 7 + 7 + 7
Чтобы составить множитель 3, нужно единицу повторить три раза
3 = 1 + 1 + 1
Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.
Математика множителя
В своей книге 1936 года «Общая теория занятости, интереса и денег» Кейнс написал следующее уравнение для описания взаимосвязи между доходом (Y), потреблением (C) и инвестициями (I): Y = C + I. Для любого уровня дохода люди тратят немного денег и сохраняют / инвестируют остаток.
Кейнс представлял предельную склонность к сохранению (MPS) как 1-b, а предельную склонность к потреблению (MPC) — b. Это создает уравнения C = bY и I = Y — C. Другими словами, bY определяет, сколько осталось для инвестиций. Кейнс переставлял уравнения для решения для дохода, или Y = I / (1-b).
Здесь Кейнс переопределяет Y как k, записывая k = 1 / (1-b). Это позволило Кейнсу утверждать Y = k * I. Поскольку вложение было умножено на k, Кейнс назвал k множителем. Для любой новой инъекции государственных расходов k показало взаимосвязь между изменением дохода (dY) и изменением инвестиций (dI) или dY = k * dI.
Например, если MPC = 0. 8, то k = 1 / (1 — 0. 8) = 5. Это предполагает, что любое изменение в доходе будет в пять раз больше изменений в новых инвестициях или новых государственных расходах.
Степени
Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:
2 × 2 = 4, 3 × 3 = 9.
Квадраты. Произведение двух равных множителей называется квадратом числа.
В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.
Кубы. Произведение трех равных множителей называется кубом числа.
Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.
Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.
Произведения двух равных множителей или квадраты называются вторыми степенями.
Произведения трех равных множителей или кубы называются третьими степенями, и т. д.
Функции Омега
Функция ω(n) (омега) представляет собой число различных простых множителей n, в то время как функция Ω(n) (большая Омега) представляет собой число простых множителей n, пересчитанное с учётом кратности. Если
- n=∏i=1ω(n)piαi,{\displaystyle n=\prod _{i=1}^{\omega (n)}p_{i}^{\alpha _{i}},}
тогда
- Ω(n)=∑i=1ω(n)αi.{\displaystyle \Omega (n)=\sum _{i=1}^{\omega (n)}\alpha _{i}.}
Например, 24 = 23 × 31, Так что ω(24) = 2 и Ω(24) = 3 + 1 = 4.
- ω(n) для n = 1, 2, 3, … соответственно 0, 1, 1, 1, 1, 2, 1, 1, 1, … — последовательность A001221 в OEIS.
- Ω(n) для n = 1, 2, 3, … соответственно 0, 1, 1, 2, 1, 2, 1, 3, 2, … — последовательность A001222 в OEIS.
Полный квадрат
Квадрат числа имеет то свойство, что все его простые множители имеют чётные кратности. Например, число 144 (квадрат 12) имеет простые множители
- 144=2×2×2×2×3×3=24×32.{\displaystyle 144=2\times 2\times 2\times 2\times 3\times 3=2^{4}\times 3^{2}.}
В более понятной форме:
- 144=2×2×2×2×3×3=(2×2×3)×(2×2×3)=(2×2×3)2=(12)2.{\displaystyle 144=2\times 2\times 2\times 2\times 3\times 3=(2\times 2\times 3)\times (2\times 2\times 3)=(2\times 2\times 3)^{2}=(12)^{2}.}
Поскольку каждый простой множитель присутствует здесь чётное число раз, исходное число можно представить в виде квадрата некоторого числа. Таким же образом, куб числа — это число, у которого кратности простых множителей делятся на три, и так далее.