Значение слова «механизм» в 10 онлайн словарях даль, ожегов, ефремова и др.

Зубчатые колеса.

Система двух находящихся в зацеплении зубчатых колес, сидящих на валах одинакового диаметра (рис. 4), в какой-то мере аналогична дифференциальному вороту (см. также ЗУБЧАТАЯ ПЕРЕДАЧА). Скорость вращения колес обратно пропорциональна их диаметру. Если малая ведущая шестерня A (к которой приложено усилие) по диаметру вдвое меньше большого зубчатого колеса B, то она должна вращаться вдвое быстрее. Таким образом, выигрыш в силе такой зубчатой передачи равен 2. Но если точки приложения усилия и нагрузки поменять местами, так что колесо B станет ведущим, то выигрыш в силе будет равен 1/2, а выигрыш в скорости – 2.

КОМБИНИРОВАННЫЕ МЕХАНИЗМЫ

Комбинированный механизм состоит из двух или большего числа простых. Это не обязательно сложное устройство; многие довольно простые механизмы тоже можно считать комбинированными. Например, в мясорубке имеются ворот (ручка), винт (проталкивающий мясо) и клин (нож-резак). Стрелки наручных часов поворачиваются системой зубчатых колес разного диаметра, находящихся в зацеплении друг с другом. Один из наиболее известных несложных комбинированных механизмов – домкрат.

Домкрат (рис. 8) представляет собой комбинацию винта и ворота. Головка винта подпирает нагрузку, а другой его конец входит в резьбовую опору. Усилие прилагается к рукоятке, закрепленной в головке винта. Таким образом, расстояние усилия равно длине окружности, описываемой концом ручки. Длина окружности дается выражением 2pr, где p = 3,14159, а r – радиус окружности, т.е. в данном случае длина ручки. Очевидно, что чем длиннее ручка, тем больше идеальный выигрыш в силе. Расстояние, проходимое нагрузкой за один оборот ручки, равно шагу резьбы. В идеале можно получить очень большой выигрыш в силе, если длинную ручку сочетать с малым шагом резьбы. Поэтому несмотря на малый КПД домкрата (около 25%) он дает большой реальный выигрыш в силе.

Выигрыш в силе, создаваемый комбинированным механизмом, равен произведению выигрышей отдельных механизмов, входящих в его состав. Так, идеальный выигрыш в силе (ИВС) для домкрата равен отношению длины окружности, описываемой ручкой, к шагу резьбы. Для входящего в состав домкрата ворота ИВС равен отношению длины окружности, описываемой ручкой (расстояние усилия), к длине окружности винта (расстояние нагрузки). Для винта домкрата ИВС равен отношению длины окружности винта (расстояния усилия) к шагу резьбы винта (расстоянию нагрузки). Перемножая ИВС отдельных механизмов домкрата, получаем для комбинированного механизма

ИВС = (Окружность ручки/Окружность винта) ґ

(Окружность винта/Шаг резьбы) = (Окружность ручки/Шаг резьбы).

Для более сложных комбинированных механизмов вычислить ИВС труднее. Поэтому для них обычно указывают лишь реальный выигрыш. См. также КУЛАЧКОВЫЙ МЕХАНИЗМ; ДИНАМИКА; СТАНКИ МЕТАЛЛОРЕЖУЩИЕ; МЕХАНИКА.

В словаре Д.Н. Ушакова

МЕХАНИ́ЗМ, механизма, ·муж. (от ·греч. mechane — машина).1. Внутреннее устройство машины или прибора, приводящее машину, прибор в действие (тех.). Механизм часов. Передаточный механизм. Заводной механизм. Механизм машины в порядке.2. перен. Внутреннее устройство, система функционирования чего-нибудь, аппарат какого-нибудь вида деятельности (·книж. ). Канцелярский механизм. Сложный механизм языка. Механизм умственной работы.II. МЕХАНИ́ЗМ, механизма, мн. нет, ·муж. (сравни механизм1) (филос.). Философское направление, сводящее всё многообразие бытия к простым законам механики.

Литература

Артоболевский И. И. Теория машин и механизмов. М. Наука 1988
Reuleaux, «Der Konstrukteur»; его же, «Theoretische Kinematik»; Burmester, «Lehrbuch der Kinematik»; Grashof, «Theoretische Maschinenlehre»;
Евневич, «Курс прикладной механики»;
Вейсбах, «Практическая механика» (в переводе Усова); Weisbach, «Lehrbuch der lugenieur und Maschinenmechanik, bearbeitet von Herrmann»; Collignon, «Traité de Mécanique»;
Чебышёв, «О простейшей суставчатой системе» («Записки Императорской академии наук», приложение к LX тому) и многие другие статьи в «Записках Императорской академии наук»;
Альбицкий, «Конические зубчатые колеса», «Цилиндрические зубчатые колеса», «Винтовое зацепление»;
Гохман, «Теория зацеплений»;
Kempe, «How to draw a straight line» («The Nature», т. XVI). Литература шарнирных механизмов указана в статье Лигина «Liste des travaux sur les systèmes articulés» («Bulletin Darboux», 2 сер., т. V II).

Рычаг.

Это жесткий стержень, который может свободно поворачиваться относительно неподвижной точки, называемой точкой опоры. Примером рычага могут служить лом, молоток с расщепом, тачка, метла.

Рычаги бывают трех родов, различающихся взаимным расположением точек приложения нагрузки и усилия и точки опоры (рис. 1). Идеальный выигрыш в силе рычага равен отношению расстояния D_E от точки приложения усилия до точки опоры к расстоянию D_L от точки приложения нагрузки до точки опоры. Для рычага I рода расстояние D_E обычно больше D_L, а поэтому идеальный выигрыш в силе больше 1. Для рычага II рода идеальный выигрыш в силе тоже больше единицы. Что же касается рычага III рода, то величина D_E для него меньше D_L, а стало быть, больше единицы выигрыш в скорости.

Винт.

Резьба винта (рис. 7) – это, в сущности, наклонная плоскость, многократно обернутая вокруг цилиндра. В зависимости от направления подъема наклонной плоскости винтовая резьба может быть левой (A) или правой (B). Сопрягающаяся деталь, естественно, должна иметь резьбу такого же направления. Примеры простых устройств с винтовой резьбой – домкрат, болт с гайкой, микрометр, тиски.

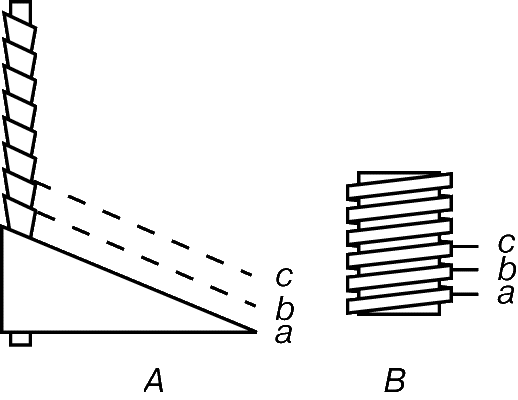
Поскольку резьба – наклонная плоскость, она всегда дает выигрыш в силе. Идеальный выигрыш равен отношению расстояния, проходимого точкой приложения усилия за один оборот винта (длины окружности), к расстоянию, проходимому при этом нагрузкой по оси винта. За один оборот нагрузка перемещается на расстояние между двумя соседними витками резьбы (a и b или b и c на рис. 7), которое называется шагом резьбы. Шаг резьбы обычно значительно меньше ее диаметра, так как иначе слишком велико трение.

Доброкачественные новообразования кожи

Если новообразования медленно растут или вовсе остаются неизменными в течение всей жизни, то они называются доброкачественными. Их отличием является и то, что клетки кожи в очаге сохраняют свои первоначальные функции. Доброкачественные — не проникают в близлежащие ткани, а только могут их сдавливать. Их структура схожа с соседними клетками, из которых они и произошли. Такие образования хорошо поддаются аппаратному и хирургическому лечению. Рецидивы отмечаются редко, но есть риск перехода в злокачественную форму.

Липома

Еще называется жировиком, поскольку развивается из жировой ткани. Этот вид очень распространен. Новообразование возникает практически на любой части тела, но на животе и ногах отмечается редко. Человеку липома не доставляет особого дискомфорта, потому как не сопровождается болью. Шишка лишь портит эстетический вид кожи. Признаки липомы:

наличие под кожей уплотнения размером 0,5-15 см;
высокая подвижность новообразования, медленный его рост;
отсутствие боли даже при механическом воздействии;
при постоянном трении жировика об одежду возможно развитие воспаления и нагноений.

Папиллома

Это новообразование представляет собой бородавку в виде узелка или сосочка. Природа возникновения – вирусная. Патологию вызывает вирус папилломы человека (ВПЧ). Он активизируется на фоне ослабленного иммунитета, вегетативных расстройств, стрессов. Внешне папиллома бывает разной. Это наросты светлого, серого или темно-коричневого цвета. Данная группа разделяется на несколько типов:

Плоские бородавки. Самый распространенный тип. Над кожей бородавки возвышаются только на 1-2 мм.
Остроконечные кондиломы. По внешнему виду напоминают цветную капусту. Чаще появляются на половых органах, вокруг заднего прохода, на слизистой рта.
Обыкновенные бородавки. Внешне похожи на плоские, но возвышаются над кожей на 2-3 мм. Поверхность бородавок шершавая.

Гемангиома

Развивается из скопления клеток внутренней поверхности сосудов. Большинство гемангиом являются одиночными, но иногда отмечается и их появление группами. В качестве мест локализации образование выбирает волосистую часть головы, веки, лоб, щеки, нос и шею. Существует несколько видов гемангиом:

Капиллярная. Располагается на поверхности кожи, может достигать больших размеров. Ее цвет варьируется от синюшно-черного до красного. Рост происходит в стороны.
Кавернозная. Это гемангиома в глубоких слоях кожи. Представляет собой ограниченное подкожное образование узловатой структуры. Цвет – от обычного оттенка кожи до синюшного.
Комбинированная. Сочетает две предыдущие формы.
Смешанная. Сосудистое образование на коже, затрагивающее и окружающие ткани, чаще – соединительную.

Лимфангиома

Образуется из стенок лимфатических сосудов. Возникает у детей еще при развитии в утробе матери. Лимфангиома чаще диагностируется в возрасте до 3 лет. Само образование – это тонкостенная полость 1-5 мм. Лимфангиома бывает нескольких видов:

Кистозной. Состоит из изолированных или сообщающихся кист. Чаще отмечается на шее в области лимфоузлов.
Кавернозной. Это небольшие по размеру образования, скрытые нетронутым кожным покровом. Обнаруживаются только на ощупь.
Капиллярной. Появляется такое новообразование на лице. Границы размыты, размеры – небольшие. Частое место локализации новообразования на коже лица – около верхней губы или на щеках.

Дерматофиброма

Другое название – просто фиброма. Мягкому типу этой опухоли более подвержены женщины молодого и зрелого возраста. Существует и твердая фиброма. Размер — не более 3 см. Внешне оно представляет собой глубоко впаянный узелок. Он выступает над поверхностью эпидермиса, имеет серый, бурый или сине-черный цвет. На ощупь фиброма гладкая, но бывает и бородавчатой. В зависимости от формы симптомы этой опухоли следующие:

Твердая фиброма. Отличается низким уровнем подвижности, бывает одиночной или множественной. Отмечается на разных частях тела и конечностей.
Мягкая фиброма. Это своеобразный мешочек на ножке розового или коричневого цвета. Чаще локализуется в области подмышек, около молочных желез и половых органов.

Пигментный невус

Родинки или невусы бывают приобретенными и врожденными. По структуре это скопления клеток с избытком меланина. Родинки различаются по цвету, форме, текстуре поверхности. Опасность некоторых из них заключается в возможном перерождении в меланому. Особенно высок риск у пигментного невуса. Его основные особенности и характеристики:

он представляет собой плоский коричневый или серый узелок;
его поверхность сухая и неровная;
пигментный невус удаляют хирургическим вмешательством.

Кератоакантома

Так называется опухолеподобный гиперкератоз. Он представляет собой доброкачественное новообразование кожного покрова эпидермального происхождения, которое имеет тенденцию к злокачественному перерождению. Внешне кератоакантома – это узел овальной или круглой формы. В основании он широкий, а по цвету совпадает с кожным покровом. Другие характеристики этой опухоли:

в центре заполнена ороговевшими клетками;
имеет приподнятые края, которые образуют своеобразный валик;
иногда цвет опухоли меняется на синюшно-красный или розовый;
диаметр достигает 2-3 см.

Лентиго

Это доброкачественные пигментные пятна. Они появляются в результате сосредоточения меланина в хроматофорах дермы и пролиферативного нарушения в базальном слое эпидермиса. Внешне лентиго выглядит, как скопление коричневых пятен с четким контуром и округлой формой. Патология возникает у подростков и пожилых людей. Основные признаки лентиго:

круглая форма пятен, размер их не превышает 2 см;
пятнышки не группируются, каждое имеет свои контуры;
язвы, шелушение и зуд отсутствуют;
пятна образуются на открытых частях тела, на половых органах и спине – редко.

Атерома

Представляет собой кисту сальной железы. Частые места локализации патологии – части тела, где высокая концентрация сальных желез, такие как:

шея;
спина;
паховая область;
волосистая часть головы.

Внешне атерома – плотное образование, имеющее четкие границы. При пальпации оно подвижное и эластичное. Атерома не приносит человеку дискомфорт. Состояние ухудшается при воспалении новообразования но коже. В этом случае отмечается нагноение, отек и покраснение тканей. На фоне этого может повыситься температура и появиться болезненность атеромы. Она самостоятельно прорывается с выделением гноя. При такой кисте есть риск развития липосаркомы – злокачественного образования.

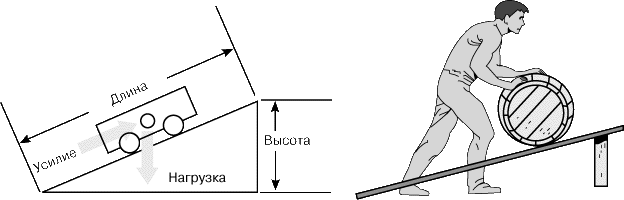
Наклонная плоскость.

Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия. К таким устройствам относятся пандусы, эскалаторы, обычные лестницы, а также конвейеры (с роликами для уменьшения трения).

Идеальный выигрыш в силе, обеспечиваемый наклонной плоскостью (рис. 5), равен отношению расстояния, на которое перемещается нагрузка, к расстоянию, проходимому точкой приложения усилия. Первое есть длина наклонной плоскости, а второе – высота, на которую поднимается груз. Поскольку гипотенуза больше катета, наклонная плоскость всегда дает выигрыш в силе. Выигрыш тем больше, чем меньше наклон плоскости. Этим объясняется то, что горные автомобильные и железные дороги имеют вид серпантина: чем меньше крутизна дороги, тем легче по ней подниматься.

Элементы механизмов

Такая совокупность двух тел, в которой формой одного тела определяется весь ряд последовательных положений, которые способно в нём занять другое тело, называется кинематической парой. Тела, составляющие пару, называются её звеньями. Например, тело, имеющее призматический канал, и помещённая в этот канал призма составляют поступательную пару, потому что одно из этих тел может совершать относительно другого только поступательное движение. Цилиндрическая втулка и размещённый в ней шип (снабжённый закраинами, не дающими ему выскочить из втулки) составляют вращательную пару. Винт и гайка составляют винтовую пару; расстояние между нарезками винта, считаемое по направлению оси винта, называют его шагом (обойдя винт один раз, нарезка приближается к концу винта на один шаг). Заметим, что поступательную пару можно формально трактовать как винтовую, шаг которой равен бесконечности, а вращательную пару — как винтовую с шагом, равным нулю.

Перечисленные кинематические пары называются простыми; отличительное свойство их — в том, что относительное движение одного их звена по отношению к другому тождественно с относительным движением второго звена по отношению к первому.

Кинематические пары, не обладающие этим свойством, называются высшими. Таковы: зацепляющиеся между собой зубчатые колёса, шкив и перекинутый через него ремень, дуговой двухсторонник и полая трёхгранная призма и многие другие. Применительно к высшим кинематическим парам используют такую терминологию: движение звена A относительно звена B называется обращённым по отношению к движению звена B относительно звена A.

Одну из наиболее интересных высших пар представляет собой эллиптический циркуль. Он состоит из доски, в которой сделаны два крестообразно пересекающихся между собой прямолинейных, перпендикулярных друг к другу прореза, и из стержня с выступающими на концах цилиндрическими шипами, диаметры которых равны ширине прорезов. Стержень вставляется шипами в прорезы так, чтобы один шип ходил по одному, а другой по другому из прорезов; с противоположной стороны на шипы навинчиваются винты с головками, препятствующими шипам выскочить из прорезов. При неподвижности доски траектории всех точек стержня суть эллипсы (частные случаи: траектории центров шипов — прямые линии, траектория середин стержня — окружность). Движение стержня относительно доски происходит так, как будто бы соединённый с ним круг, построенный на нём как на диаметре, катился по внутренней стороне окружности, описанной из точки пересечения средних линий прорезов радиусом, равным диаметру катящегося круга. При этом в обращённом движении (т. е. при неподвижности стержня) все точки доски описывают улитки Паскаля.

Звено B, соединённое в какую-либо пару со звеном A, может быть соединено в пару же со звеном C, которое, в свою очередь, может составлять пару со звеном D и так далее. Такое последовательное соединение звеньев в пары называется кинематической цепью. Если последнее звено кинематической цепи соединено в пару с первым, то цепь называется замкнутой, в противном случае она называется открытой.

Кинематическая замкнутая цепь, получающая при неподвижности одного из звеньев вполне определённое движение, характеризующее механизм, называется принудительной. Когда в принудительной цепи одно из звеньев предполагается неподвижным, то говорят, что цепь поставлена на этом звене. Ставя принудительную цепь последовательно на разные её звенья, получим столько механизмов, сколько имеется звеньев в цепи. Примером принудительной цепи может служить шарнирный четырёхзвенник, состоящий из четырёх стержней, соединённых между собой вращательными парами, называемыми шарнирами.

Литература

Артоболевский И. И. Теория машин и механизмов. М. Наука 1988
Reuleaux, «Der Konstrukteur»; его же, «Theoretische Kinematik»; Burmester, «Lehrbuch der Kinematik»; Grashof, «Theoretische Maschinenlehre»;
Евневич, «Курс прикладной механики»;
Вейсбах, «Практическая механика» (в переводе Усова); Weisbach, «Lehrbuch der lugenieur und Maschinenmechanik, bearbeitet von Herrmann»; Collignon, «Traité de Mécanique»;
Чебышёв, «О простейшей суставчатой системе» («Записки Императорской академии наук», приложение к LX тому) и многие другие статьи в «Записках Императорской академии наук»;
Альбицкий, «Конические зубчатые колеса», «Цилиндрические зубчатые колеса», «Винтовое зацепление»;
Гохман, «Теория зацеплений»;
Kempe, «How to draw a straight line» («The Nature», т. XVI). Литература шарнирных механизмов указана в статье Лигина «Liste des travaux sur les systèmes articulés» («Bulletin Darboux», 2 сер., т. V II).

Элементы механизмов

В словаре Д.Н. Ушакова

МЕХАНИ́ЧЕСКИЙ, механическая, механическое (·книж. ).1. прил. к механика в 1 ·знач. Механические законы.| Основанный на принципах, законах механики. Механическое воздействие на природу.2. прил. к механизм» title=’что такое механизм, значение слова механизм в словаре Ушакова’>механизм1 в 1 ·знач.; действующий при посредстве механизмов, машин. Механическое оборудование. Механическая сила. Механический»>Механический труд.3. (в качестве ·кратк. употр. механичен, механична, механично). Машинальный, автоматический. Механическое запоминание. Механические движения. Механически (нареч.) заучить что-нибудь.4. употр. неточно вместо механистический. Механическое понимание природы.

Блок.

Это колесо с желобом по окружности для каната или цепи. Блоки применяются в грузоподъемных устройствах. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспастом. Одиночный блок может быть либо с закрепленной осью (уравнительным), либо подвижным (рис. 2). Блок с закрепленной осью действует как рычаг I рода с точкой опоры на его оси. Поскольку плечо усилия равно плечу нагрузки (радиус блока), идеальный выигрыш в силе и скорости равен 1. Подвижный же блок действует как рычаг II рода, поскольку нагрузка расположена между точкой опоры и усилием. Плечо нагрузки (радиус блока) вдвое меньше плеча усилия (диаметр блока). Поэтому для подвижного блока идеальный выигрыш в силе равен 2.

Более простой способ определения идеального выигрыша в силе для блока или системы блоков – по числу параллельных концов каната, удерживающих нагрузку, как это нетрудно сообразить, взглянув на рис. 2.

Уравнительные и подвижные блоки можно сочетать по-разному для увеличения выигрыша в силе. В одной обойме можно установить два, три или большее число блоков, а конец троса можно прикрепить либо к неподвижной, либо к подвижной обойме.

Литература

Артоболевский И. И. Теория машин и механизмов. М. Наука 1988
Reuleaux, «Der Konstrukteur»; его же, «Theoretische Kinematik»; Burmester, «Lehrbuch der Kinematik»; Grashof, «Theoretische Maschinenlehre»;
Евневич, «Курс прикладной механики»;
Вейсбах, «Практическая механика» (в переводе Усова); Weisbach, «Lehrbuch der lugenieur und Maschinenmechanik, bearbeitet von Herrmann»; Collignon, «Traité de Mécanique»;
Чебышёв, «О простейшей суставчатой системе» («Записки Императорской академии наук», приложение к LX тому) и многие другие статьи в «Записках Императорской академии наук»;
Альбицкий, «Конические зубчатые колеса», «Цилиндрические зубчатые колеса», «Винтовое зацепление»;
Гохман, «Теория зацеплений»;
Kempe, «How to draw a straight line» («The Nature», т. XVI). Литература шарнирных механизмов указана в статье Лигина «Liste des travaux sur les systèmes articulés» («Bulletin Darboux», 2 сер., т. V II).