Линейное программирование

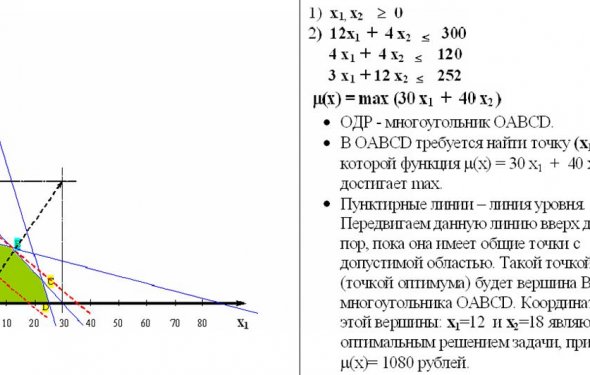
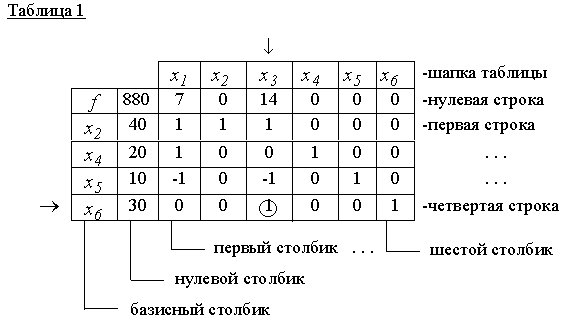
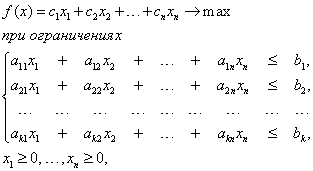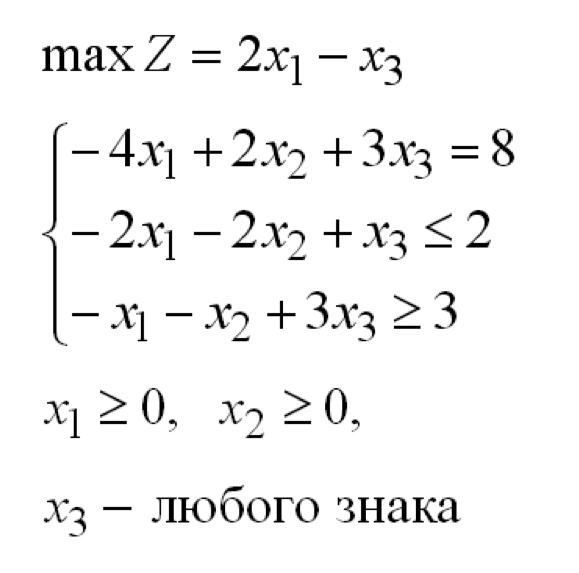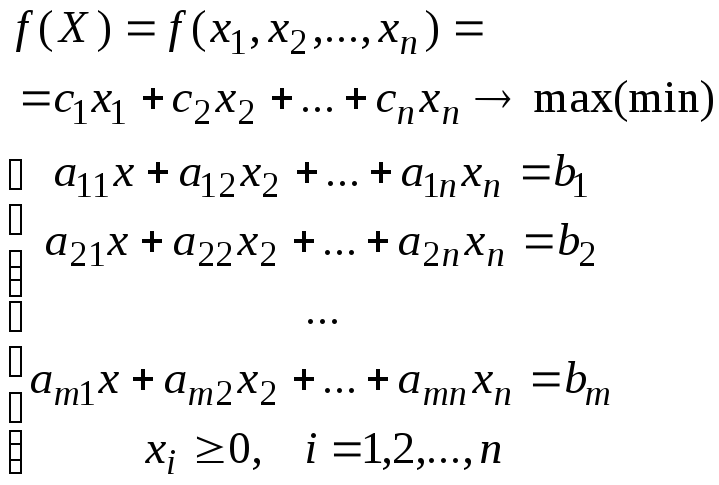ПРЕДИСЛОВИЕ

Реальные объекты слишком сложны, поэтому для их исследования создают различные модели. С одной стороны, в каждой из них необходимо отразить существенные черты реального объекта. Но с другой – модели должны быть доступными для изучения, т.е. не слишком сложными, что приводит к упрощенным копиям реального мира. В силу такой двойственности задачи составление моделей во многом является искусством. Чем удачнее построена модель, тем полезнее вытекающие из этого исследования выводы и рекомендации. Составление математических моделей и называется математическим моделированием.

Методические указания и задания к контрольной работе по линейному программированию помогут студентам освоить задачи оптимизации наиболее важной области математических моделей и методов. Применение методов оптимизации предполагает предварительное описание некоторого объекта или процесса, составление его математической модели, выбор соответствующего математического метода решения, его алгоритмическую реализацию, а также анализ результатов решения

В данном издании авторы в сжатой и доступной форме изложили теоретический материал по курсу “Линейное программирование”. Основные теоретические положения наглядно проиллюстрированы решением большого числа примеров и задач. Некоторые задания подобраны таким образом, чтобы можно было самих себя проконтролировать, овладев при этом необходимыми знаниями. Если в ходе усвоения материала возникнут вопросы, можно задать их на консультациях, которые будут проводиться по субботам. Авторы надеются, что данное пособие поможет студентам самостоятельно выполнить контрольную работу по линейному программированию и успешно справиться с экзаменом.

Переход от задачи минимизации целевой функции к задаче максимизации

F(x) → min

F(x) → max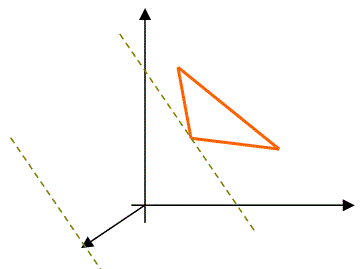

Опорный планБазисный планОптимальный план

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Пример №1. Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x₁ + 2x₂ — 2x₃ → min при ограничениях:4x₁ + 3x₂ — x₃≤10- 2x₂ + 5x₃≥3x₁ + 2x₃=9Для приведения ЗЛП к канонической форме необходимо:1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x₄; во втором неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус. 4x₁ + 3x₂-1x₃ + 1x₄ + 0x₅ = 100x₁-2x₂ + 5x₃ + 0x₄-1x₅ = 31x₁ + 0x₂ + 2x₃ + 0x₄ + 0x₅ = 9F(X) = — x₁ — 2x₂ + 2x₃Переход к СЗЛП.Расширенная матрица системы ограничений-равенств данной задачи:

4	3	-1	1	10
-2	5	-1	3
1	2	9

₄₂₂₂₂

4-(0 • 3):-2	3-(-2 • 3):-2	-1-(5 • 3):-2	1-(0 • 3):-2	0-(-1 • 3):-2	10-(3 • 3):-2
0 : -2	-2 : -2	5 : -2	0 : -2	-1 : -2	3 : -2
1-(0 • 0):-2	0-(-2 • 0):-2	2-(5 • 0):-2	0-(0 • 0):-2	0-(-1 • 0):-2	9-(3 • 0):-2

4	61/2	1	-11/2	141/2
1	-21/2	1/2	-11/2
1	2	9

₃₃₃₃

4-(1 • 61/2):2	0-(0 • 61/2):2	61/2-(2 • 61/2):2	1-(0 • 61/2):2	-11/2-(0 • 61/2):2	141/2-(9 • 61/2):2
0-(1 • -21/2):2	1-(0 • -21/2):2	-21/2-(2 • -21/2):2	0-(0 • -21/2):2	1/2-(0 • -21/2):2	-11/2-(9 • -21/2):2
1 : 2	0 : 2	2 : 2	0 : 2	0 : 2	9 : 2

3/4	1	-11/2	-143/4
11/4	1	1/2	93/4
1/2	1	41/2

3₄₁₄1₂₅3₄1₄₁₂1₂₅3₄1₂₁₃1₂₄3₄₁1₂₅3₄₂1₄₁1₂₅3₄₃1₂₁1₂₁1₄₁1₂₅3₄1₂₁1₂1₂₁₅1₂3₄₁1₂₅3₄1₄₁1₂₅3₄1₂₁1₂3₄₁1₂₅3₄1₄₁1₂₅3₄1₂₁1₂1₂₁₅1₂3₄₁1₂₂3₄1₄₁1₂₂3₄1₂₁1₂1₂₁₂1₂

Пример №2. Найдите сначала графическим методом, а затем симплекс-методом решение задачи
F(X) = x₁ + x₂ — x₃ + x₅+15 → max (min) при ограничениях:
-3x₁ + x₂ + x₃=3
4x₁ + 2x₂ — x₄=12
2x₁ — x₂ + x₅=2
x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0, x₄ ≥ 0, x₅ ≥ 0

Дополнительный застой

Возможно получить оптимальное решение двойного, когда только оптимальное решение основного известно, используя дополнительную теорему застоя. Государства теоремы:

Предположим, что x = (x, x…, x) основной выполнимый и что y = (y, y…, y) двойной выполнимый. Позвольте (w, w…, w) обозначают соответствующие основные слабые переменные и позволяют (z, z…, z) обозначают соответствующие двойные слабые переменные. Тогда x и y оптимальны для их соответствующих проблем если и только если

• x z = 0, для j = 1, 2…, n, и
• w y = 0, поскольку я = 1, 2…, m.

Таким образом, если i-th слабеют, переменная основного не ноль, то i-th переменная двойного равна нолю. Аналогично, если j-th слабеют, переменная двойного не ноль, то j-th переменная основного равна нолю.

Это необходимое условие для optimality передает довольно простой экономический принцип. В стандартной форме (максимизируя), если там слабо в ограниченном основном ресурсе (т.е., есть «остатки»), то у дополнительных количеств того ресурса не должно быть стоимости. Аналогично, если там слабо в двойном (теневом) ценовом ограничительном требовании неотрицательности, т.е., цена не ноль, то должны быть недостаточные поставки (никакие «остатки»).

2.1. Общая задача и основные понятия линейного программирования

Задачу ЛП (1.2) и (1.3) можно представить также в виде так называемой  канонической записи задачи ЛП (2.1).

   (2.1) 

Каноническая форма задачи ЛП предполагает, что все функциональные ограничения вида (1.1) представляются в виде равенств. Переход от ограничений типа неравенств к ограничениям типа равенств осуществляется с помощью искусственных переменных yi , на которые, чтобы сохранить смысл ограничений, накладываются условия неотрицательности.

В матричной форме каноническую форму задачи ЛП можно представить в следующем виде (2.2):

  , где E – единичная матрица  (2.2)

или

,  (2.3)

где  — единичный вектор m-мерного векторного пространства, т. е. , а Ai– i-ый вектор-столбец матрицы условий A.

Решение (x, y)’ называется опорным (базисным) решением задачи (1.2) –(1.3), если система векторов {Aj, ei}, входящих в выражение *) в представлении (2.3)  с положительными компонентами , , линейно независима.

Совокупность линейно независимых векторов столбцов матрицы компонентов условий Aj и единичных векторов ei, соответствующих положительным компонентам  и , называется базисом опорного решения (x, y)’.

Из теории линейного программирования известно, что опорные решения задачи ЛП соответствуют крайним точкам выпуклого многогранника, являющегося множеством допусимых решений задачи ЛП, и наоборот.

Пример 2.1. Рассмотрим некоторые опорные решения в следующей задаче.

Очевидно, что , причем  n=3, m=2.

Геометрически ограничения задачи Примера 2.1 можно представить в виде графика в трехмерном пространстве (рис. 2.1). Точки M0, M1, M2, M3 являются крайними точками выпуклого многогранника в виде усеченной сверху прямоугольной пирамиды — множества допустимых решений задачи. Точка M4 – крайней точкой не является.

Покажем, что в данной задаче решения, соответствующие крайним точкам M1 и M2, являются опорными, тогда как решение, соответствующее точке  M4,  опорным не является.

Рисунок 2.1 – Геометрическое представление условий задачи Примера 2.1.

В канонической форме рассматриваемая задача выглядит следующим образом:

  i = 1 (номер ограничения)

  i = 2

  i = 3

  i = 4

  i = 5

  i = 6

  i = 7

( ).

Матрицу условий можно представить как:

а) Рассмотрим  точку  , в канонической форме задачи  .  При этом легко показать, что векторы столбцы матрицы условий ,  – линейно независимы.

б) Рассмотрим  точку  , в канонической форме задачи  . Легко показать, что векторы столбцы A3 и e1 линейно независимы.

в) Рассмотрим  точку ,  , в канонической форме задачи  , в этом случае векторы столбцы A1, A2 и e2 , соответствуюшие положительным компонентам решения, очевидно  линейно зависимы.

Можно получить частное опорное решение задачи (3.4), приравняв все  (получаем n уравнений и m неизвестных). 

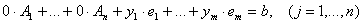
Отсюда можно выразить переменные  : , т. е

В примере  1 такой точкой является  точка пересечения координат, в терминах канонической формы это точка ,  причем очевидно, что векторы-столбцы,  соответствующие положительным компонентам A4 и A5 линейно независимы.

Опорное решение (x, y)’ задачи ЛП (3.4) называется невырожденным, если оно содержит ровно m положительных компонент. Если решение (x, y)’ содержит менее m положительных компонент, оно называется вырожденным.

Примечание: если решение (x, y)’ содержит более m положительных компонент, оно не является опорным.

Геометрически невырожденность решения задачи ЛП (1.2) – (1.3.) означает, что в этой крайней точке (вершине) многогранника пересекается ровно n+m граничных гиперплоскостей. Если опорное решение вырождено, то в соответствующей вершине пересекаются более чем n+m гиперплоскостей.

Пример 2. 2.

  ()

В канонической форме

  i = 1

  i = 2

  i = 3

  i = 4

  i = 5

  i = 6

  i = 7

Каждая крайняя точка выпуклого многогранника – допусимого множества получается пересечением 5 гиперплоскостей  в 5-мерном векторном пространстве из 7 заданных в задаче.

Рисунок 2.2 – Геометрическое представление вырожденного опорного  решения.

Рассмотрим точки M3  и M2 и соответствующие им опорные решения (рис.2.2). В каноническом представлении задачи Примера 1.2 точка M3 имеет следующие координаты:

 -и представляет собой пересечение гиперплоскостей с номерами 1, 2, 4, 5, 6 (число гиперплоскостей равно 5).

Точка  — является пересечением 6  гиперплоскостей с номерами 1, 2, 3, 4, 6, 7. Очевидно, что соответствующее ей опорное решение является вырожденным (число гиперплоскостей больше 5).

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Покрытие/упаковка дуальностей

Закрывающая LP — линейная программа формы:

: Минимизируйте:

: Согласно:

таким образом, что матрица A и векторы b и c неотрицательная.

Двойной из закрывающей LP является упаковывающая вещи LP, линейная программа формы:

: Максимизируйте:

: Согласно:

таким образом, что матрица A и векторы b и c неотрицательная.

Примеры

Покрытие и упаковка LP обычно возникают как линейное программное смягчение комбинаторной проблемы и важны в исследовании алгоритмов приближения. Например, смягчение LP упаковочной проблемы набора, независимой проблемы набора и соответствующей проблемы упаковывает LP. Смягчение LP проблемы покрытия набора, проблемы покрытия вершины и проблемы набора доминирования также покрывает LP.

Нахождение фракционной окраски графа является другим примером закрывающей LP. В этом случае есть одно ограничение для каждой вершины графа и одной переменной для каждого независимого набора графа.

Открытые проблемы и недавняя работа

Есть несколько открытых проблем в теории линейного программирования, решение которого представляло бы фундаментальные прорывы в математике и потенциально важные шаги вперед в нашей способности решить крупномасштабные линейные программы.

• LP допускает решительно многочленно-разовый алгоритм?
• LP допускает, что решительно многочленный алгоритм находит строго дополнительное решение?
• LP допускает многочленный алгоритм в действительном числе (себестоимость единицы продукции) модель вычисления?

Этот тесно связанный набор проблем был процитирован Стивеном Смейлом в качестве среди 18 самых больших нерешенных проблем 21-го века. В словах Смейла третья версия проблемы «является главной нерешенной проблемой линейной программной теории». В то время как алгоритмы существуют, чтобы решить линейное программирование в слабо многочленное время, такое как эллиптические методы и методы внутренней точки, никакие алгоритмы еще не были найдены, которые позволяют решительно многочленно-разовую работу в числе ограничений и числе переменных. Развитие таких алгоритмов представляло бы большой теоретический интерес, и возможно позволило бы практическую прибыль в решении больших LP также.

Хотя догадка Хёрш была недавно опровергнута для более высоких размеров, она все еще оставляет следующие вопросы открытыми.

Есть ли правила центра, которые приводят к многочленно-разовым Симплексным вариантам?

всех polytopal графов есть многочленным образом ограниченный диаметр?

Эти вопросы касаются исполнительного анализа и развития подобных Симплексу методов. Огромная эффективность Симплексного алгоритма на практике несмотря на его показательно-разовую теоретическую работу намекает, что могут быть изменения Симплекса, которые бегут в полиномиале или даже решительно многочленное время. Это имело бы большое практическое и теоретическое значение знать, существуют ли какие-либо такие варианты, особенно как подход к решению, если LP может быть решена в решительно многочленное время.

Симплексный алгоритм и его варианты падают в семье следующих за краем алгоритмов, так названных, потому что они решают линейные программные проблемы, двигаясь от вершины до вершины вдоль краев многогранника. Это означает, что их теоретическая работа ограничена максимальным количеством краев между любыми двумя вершинами на многограннике LP. В результате мы интересуемся знанием максимального теоретического графом диаметра polytopal графов. Было доказано, что у всех многогранников есть подпоказательный диаметр. Недавнее опровержение догадки Хёрш — первый шаг, чтобы доказать, есть ли у какого-либо многогранника супермногочленный диаметр. Если какие-либо такие многогранники существуют, то никакой следующий за краем вариант не может бежать в многочленное время. Вопросы о диаметре многогранника представляют независимый математический интерес.

Симплексные методы центра сохраняют основной (или двойной) выполнимость. С другой стороны, перекрещивающиеся методы центра не сохраняют (основной или двойной) выполнимость — они могут посетить основные выполнимые, двойные выполнимые или основные-и-двойные неосуществимые основания в любом заказе. Методы центра этого типа были изучены с 1970-х. По существу эти методы пытаются найти самый короткий путь центра на многограннике договоренности под линейной программной проблемой. В отличие от polytopal графов, у графов многогранников договоренности, как известно, есть маленький диаметр, позволяя возможность решительно многочленно-разового перекрещивающегося алгоритма центра, не решая вопросы о диаметре общих многогранников.

Дополнительные материалы для чтения

Читатель может рассмотреть начало с Неринга и Такера с первым объемом Dantzig и Thapa, или с Уильямсом.

Дмитрис Алеврас и Манфред В. Падберг, Линейная Оптимизация и Расширения: проблемы и Решения, Universitext, Спрингер-Верлэг, 2001. (Проблемы от Падберга с решениями.)

Глава 4: Линейное Программирование: стр 63-94. Описывает рандомизированный алгоритм пересечения полусамолета для линейного программирования.

• A6: MP1: ПРОГРАММИРОВАНИЕ ЦЕЛОГО ЧИСЛА, pg.245. (информатика, теория сложности)
• Бернд Гэртнер, Jiří Matoušek (2006). Понимая и Используя Линейное Программирование, Берлин: Спрингер. ISBN 3-540-30697-8 (элементарное введение для математиков и программистов)
• Кенгуру Корнелиса, Tamás Terlaky, Жан-Филипп Вяль, Методы внутренней точки для Линейной Оптимизации, Второго Выпуска, Спрингера-Верлэга, 2006. (Уровень выпускника)
• Александр Шриджвер, Теория Линейных и Программирования Целого числа. Джон Вайли & сыновья, 1998, ISBN 0-471-98232-6 (математических)
• Роберт Дж. Вэндербеи, Линейное Программирование: Фонды и Расширения, 3-й редактор, Международный Ряд в Операционном Исследовании & Менеджменте, Издании 114, Спрингере Верлэге, 2008. ISBN 978-0-387-74387-5. (Второй выпуск онлайн был раньше доступен. Сайт Вэндербеи все еще содержит обширные материалы.)
• Х. П. Уильямс, Здание Модели в Математическом Программировании, Третьем исправленном издании, 1990. (Моделирование)
• Стивен Дж. Райт, 1997, Основные двойные Методы внутренней точки, СИАМ. (Уровень выпускника)
• Йиню Е, 1997, Алгоритмы Внутренней точки: Теория и Анализ, Вайли. (Продвинутый уровень выпускника)
• Циглер, Гюнтер М., главы 1-3 и 6-7 в лекциях по многогранникам, Спрингеру-Верлэгу, Нью-Йорк, 1994. (Геометрия)

1.2. Схема построения оптимизационных моделей

Практически невозможно построить четкий  алгоритм процедуры построения оптимизационных моделей. Поэтому в данном разделе рассматриваются общие принципы построения оптимизационных моделей,

Прежде чем построить математическую модель задачи, т. е. записать ее с помощью математических символов в форме (1.1)-(1.3), необходимо четко разобраться с ситуацией, описанной в условии. Для этого необходимо в терминах решаемой задачи ответить на следующие вопросы:

1) Что является искомыми величинамизадачи? Как лучше обозначить эти величины?

2) Какова цель решения? Что в задаче служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т. д. В каком направлении должно изменяться значение этого критерия (к max или к min) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные характеристики задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т. д.

Только после ответа на все эти вопросы можно приступать к записи математической модели.

В общем виде схема построения математической модели состоит из следующих этапов.

Этап 1. Выбор и обозначение переменных задачи.

Несмотря на кажущуюся простоту этого вопроса, ответ на него далеко не всегда очевиден. Зачастую этапу построения модели предшествует долгое согласование со специалистом в соответствующей предметной областипо поводу  представления в терминах математического программирования исходной задачи,  которая, естественно,  изаначально сформулирована в терминах предметной области.

При формулировании вектора искомых переменных необходимо помнить, что речь идет о переменных величинах, которые  можно изменять целенаправленным образом, т. е. об управляемых переменных.   Можно, конечно, поставить задачу определения спроса на рынке на предлагаемый товар с целью оптимизации прибыли этой фирмы. Но попытка управлять спросом на рынке вряд ли будет успешной. Более реальная задача – прогнозирование спроса, но эта задача, уже не является задачей математического программирования, т. е. задачей планирования; скорее это задача прикладного статистического анализа, т. е. задача описания.

Получить полный текст

Искомые величины являются переменными задачи, которые, как правило, обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде x = (x1, x2, … ,xn). При этом переменные могут иметь и более чем один индекс, например, xij или xikl.

Этап 2. Представление целевой функции задачи.

Цель решения записывается в виде ЦФ, обозначаемой, например, z. Математическая формула ЦФ z отражает способ расчета значений критерия эффективности задачи.

Этап 3. Представление ограничений задачи.

Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т. е. ограничений. Левые и правые части ограничений отражают способ получения (расчет или численные значения из условия задачи) значений тех характеристик задачи, на которые были наложены соответствующие условия.

Примечания

• Л.В. Канторович: новый метод решения некоторых классов экстремальных проблем, Наука Doklady Akad СССР, 28, 1940, 211-214.
• Ф. Л. Хичкок: распределение продукта от нескольких источников до многочисленных окрестностей, Журнала Математики и Физики, 20, 1941, 224-230.
• G.B Dantzig: Максимизация линейной функции переменных подвергает линейным неравенствам, 1947. Изданные стр 339-347 в Т.К. Купмэнсе (редактор):Activity Анализ Производства и Распределения, Нью-Йорка-Лондона 1951 (Wiley & Chapman-Hall)
• Дж. Э. Бисли, редактор. Достижения в Линейном и Программирование Целого числа. Оксфордская Наука, 1996. (Коллекция обзоров)
• Р. Г. Блэнд, Новые конечные вертящиеся правила для симплексного метода, Математики. Oper. Res. 2 (1977) 103–107.
• Карл-Хайнц Боргвардт, Симплексный Алгоритм: Вероятностный Анализ, Алгоритмы и Комбинаторика, Том 1, Спрингер-Верлэг, 1987. (Среднее поведение на случайных проблемах)
• Ричард В. Коттл, редактор Основной Джордж Б. Дэнциг. Стэнфордские Деловые Книги, издательство Стэндфордского университета, Стэнфорд, Калифорния, 2003. (Отобранные статьи Джорджа Б. Дэнцига)
• Джордж Б. Дэнциг и Муканд Н. Тэпа. 1997. Линейное программирование 1: Введение. Спрингер-Верлэг.
• Джордж Б. Дэнциг и Муканд Н. Тэпа. 2003. Линейное Программирование 2: Теория и Расширения. Спрингер-Верлэг. (Алгоритмы всесторонней, покрывающей, например, вертящейся и внутренней точки, крупномасштабные проблемы, разложение после Дэнциг-Вольфа и Клещей и представления стохастического программирования.)
• Эдмондс, J. и Джайлс, R., «Макс. минутой отношение для подмодульных функций на графах», Энн. Дискретная Математика., v1, стр 185-204, 1 977
• Эвэр Д. Неринг и Альберт В. Такер, 1993, линейные программы и связанные проблемы, академическое издание. (элементарный)
• М. Падберг, Линейная Оптимизация и Расширения, Второй Выпуск, Спрингер-Верлэг, 1999. (тщательно написанный счет основных и двойных симплексных алгоритмов и проективных алгоритмов, с введением в целое число линейное программирование—показ проблемы продавца путешествия для Одиссея.)
• Кристос Х. Пэпэдимитрайоу и Кеннет Стейглиц, Комбинаторная Оптимизация: Алгоритмы и Сложность, Исправленное переиздание с новым предисловием, Дувром. (информатика)

(Приглашенный обзор, от Международного Симпозиума по Математическому Программированию.)

(Информатика)