Математический маятник

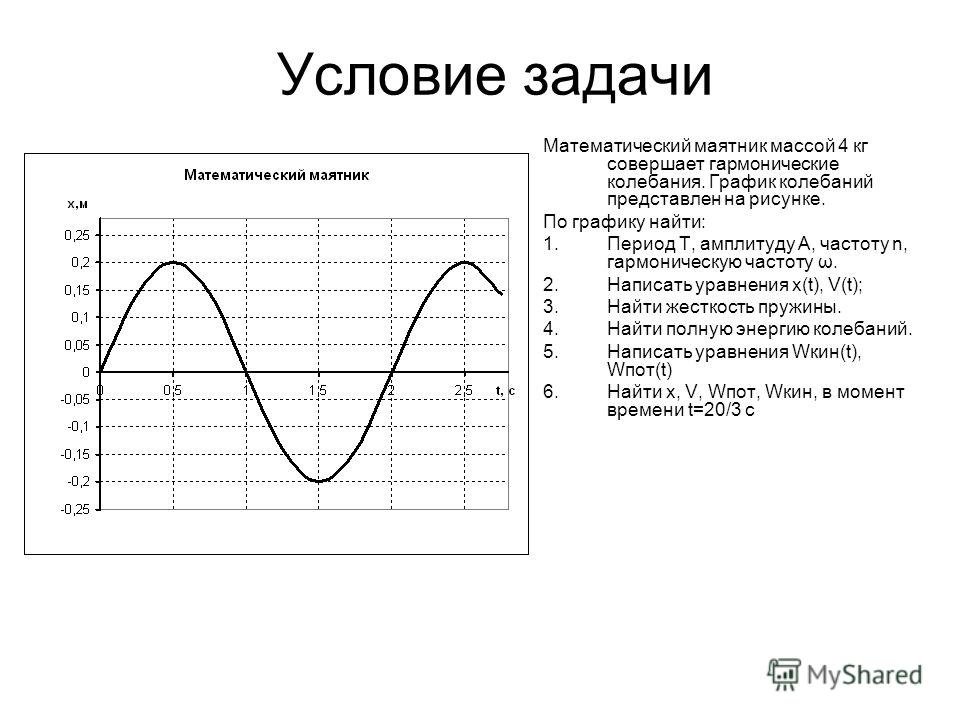
2.3. Свободные колебания. Математический маятник window.top.document.title = «2.3. Свободные колебания. Математический маятник»;

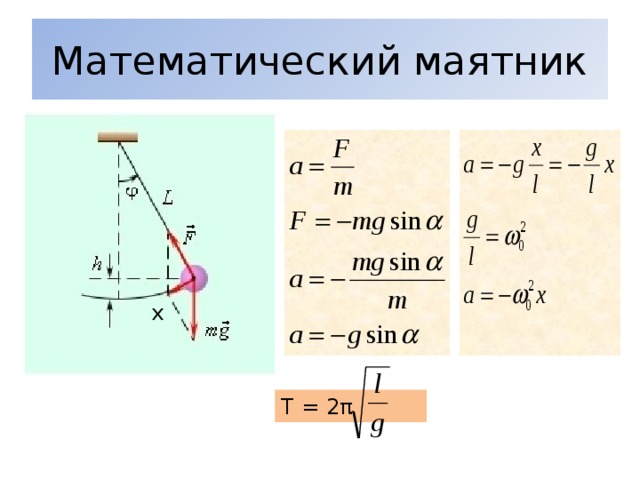
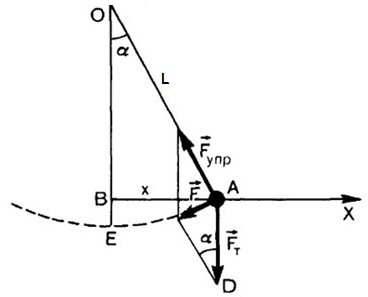
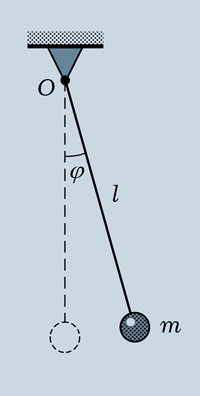
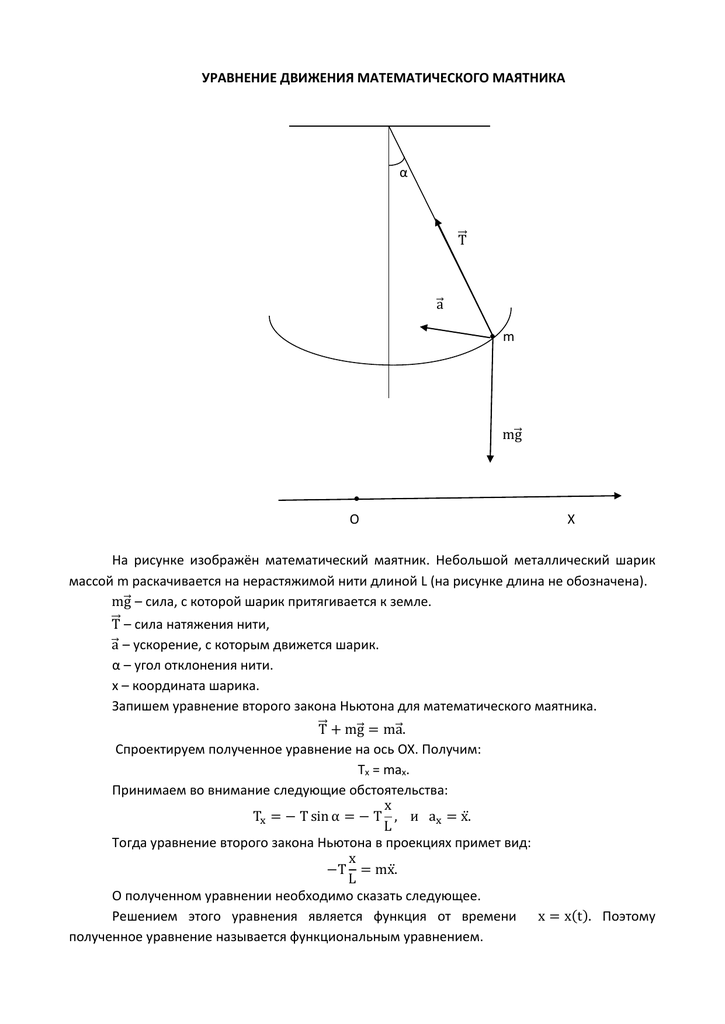
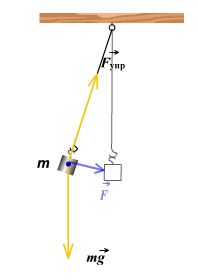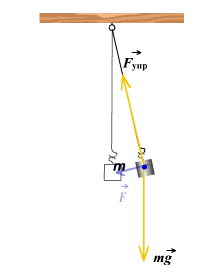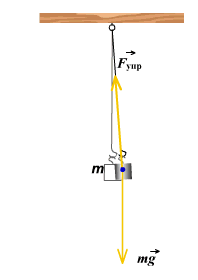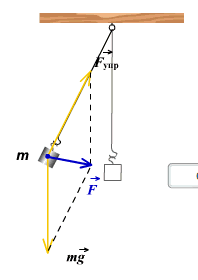
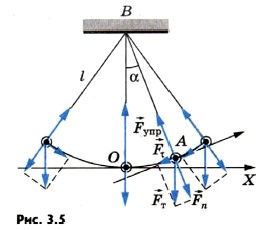
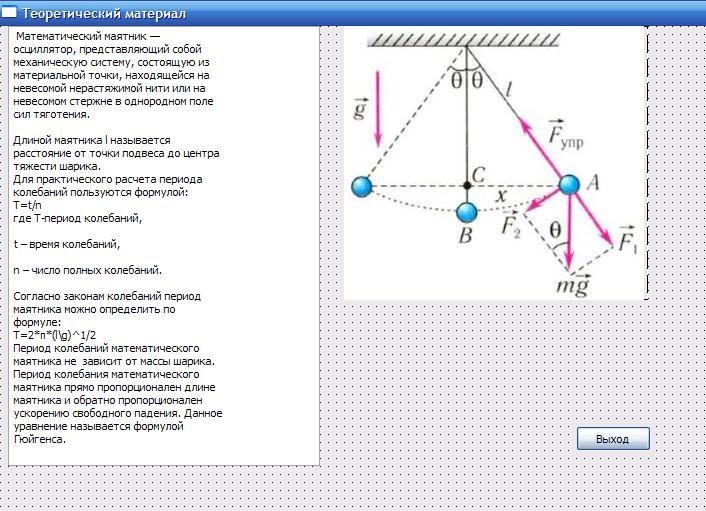
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F_τ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Рисунок 2.3.1.Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге

Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно φ = x / l. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а

Только в случае малых колебаний, когда приближенно можно заменить на математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20°; при этом величина отличается от не более чем на 2 %. Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Таким образом, тангенциальное ускорение a_τ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

Эта формула выражает собственную частоту малых колебаний математического маятника.

Следовательно,

Модель. Математический маятник

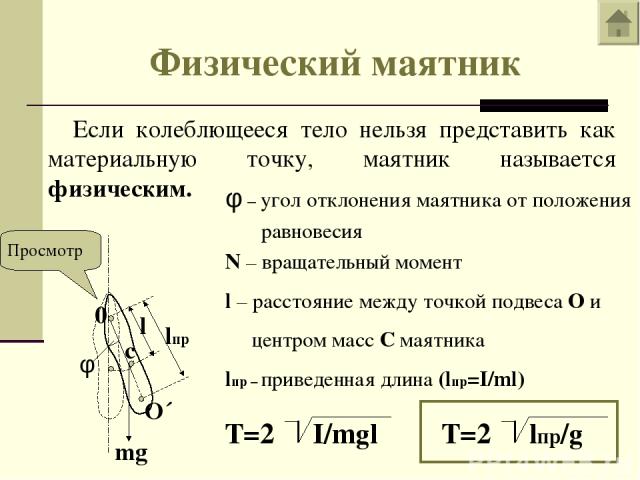
Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

Здесь d – расстояние между осью вращения и центром масс C.

Рисунок 2.3.2.Физический маятник

Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний

см. §1.23

εIO

Здесь ω – собственная частота малых колебаний физического маятника.

Следовательно,

Более строгий вывод формул для ω и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:

Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

Это уравнение свободных гармонических колебаний (). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции I_C относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:

Окончательно для круговой частоты ω свободных колебаний физического маятника получается выражение:

Что собой представляет математический маятник?

Из предыдущих уроков вы уже должны знать, что под маятником, как правило, подразумевают тело, которое совершает колебания под действием гравитационного взаимодействия. То есть, можно сказать, что в физике, под этим понятием, принято считать твердое тело, которое под действием силы тяжести совершает колебательные движения, которые происходят вокруг неподвижной точки или оси.

А вот математическим маятником можно считать такой маятник, у которого длинна такой нити, во много раз больше, чем размер подвешенного на нее тела. Также следует учесть, что по сравнению с массой тела, нить иметь ничтожно малую массу.

Электронное учебное пособие по разделу курса физики Механика

Механика– это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики. 

Физический маятник

Физическим маятником называется твердое тело, спо­собное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции (рис. 46а). В положении равновесия центр инерции С находится под точкой подвеса 0 маятника на одной с ней вертикали. При отклонении маятника от положения рав­новесия на угол j возникает вращательный момент сил, стремящийся вернуть маятник в положение равновесия. Этот момент равен

М = –mglsinj,

где m –масса маятника, а l–расстояние между точ­кой подвеса ицентром масс маятника. Знак «–» означает, что момент сил направлен против углового смещения. Уравнение вращательной динамики принимает вид:

b = М / I = – (mglI) sin j,

где I – момент  инерции   маятника  относительно оси, проходящей через точку подвеса. В случае малых колебаний (j≤ 5°) это уравнение переходит в дифференциальное урав­нение собственных незатухающих колебаний:

,

решением  которого является функция:

j = А cos (wt +a),

где через w обозначена угловая частота колебаний:

w = (mglI)1/2.

Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, угловая частота w ко­торых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния ме­жду осью вращения и центром инерции маятника. Период колебаний физического маят­ника определяется выражением:

.

Из сопоставления формул  и  следует, что математический маятник с длиной l_пр = (I/ml) имеет такой же период колебаний, как и данный физический маятник. Величину l_пр = (I/ml) называют приведенной длиной физического маятника. Итак, приведенная длина физического маятника – это длина такого математического маятника, период коле­баний которого совпадает с периодом данного физиче­ского маятника. Точка 0′ на прямой, соединяющей точку подвеса с цент­ром инерции, лежащая на расстоянии приведенной дли­ны от оси вращения, называется центром качания физического маятника. По теореме Штейнера момент инерции маятника I может быть представлен в виде

I = I + ml2,

где I – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маят­ника.

Подставив  I = I + ml2   в  l_пр = (I/ml) , получаем:  l_пр = (Iml) + l, откуда следует, что приведенная длина l_пр всегда боль­ше длины l, так что точка подвеса 0 и центр качания 0′ лежат по разные стороны от центра инерции С (центра масс). Подвесим маятник в центре качания 0′.Приведенная длина в этом случае будет равна: l_пр‘ = (Iml‘) + l‘, где l‘ – расстояние между первоначальным центром ка­чания и центром инерции маятника. Учитывая, что l‘ = l_пр – l, имеем:

l_пр‘ = Im(l_пр – l) + l_пр – l = l_пр+ [(I + ml2)  – ml_прl] /m(l_пр – l).

Выражение, стоящее в квадратных скобках, равно нулю, поскольку I + ml2 = I – это момент инер­ции относительно первоначальной оси вращения; этой же величине равно выражение ml_прl.Таким образом, мы приходим к выводу, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса 0 и центр кача­ния 0′ обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса стано­вится новым центром качания.

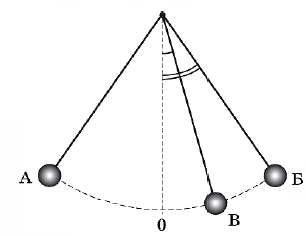
На свойстве взаимности осно­вано определение ускорения силы тяжести с помощью, так называемого оборотного маятника (рис. 46б). Оборотным на­зывается такой маятник, у которого имеются две парал­лельные друг другу, закрепленные вблизи его концов опорные призмы П₁ и П₂, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и за­крепляться на нем тяжёлые грузы – чечевицы А и В. Перемещением гру­зов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно l_пр. Измерив период колебаний маятника Т и определив l_пр, при помощи формулы  можно найти ускорение силы тяжести g

.

Решения уравнения движения

Гармонические колебания

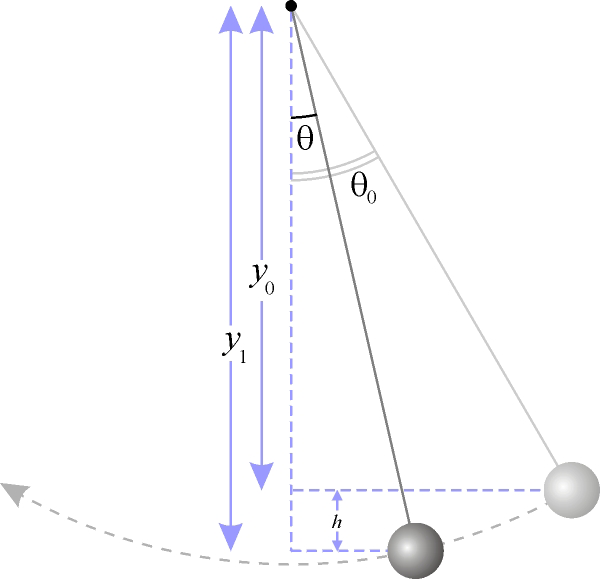
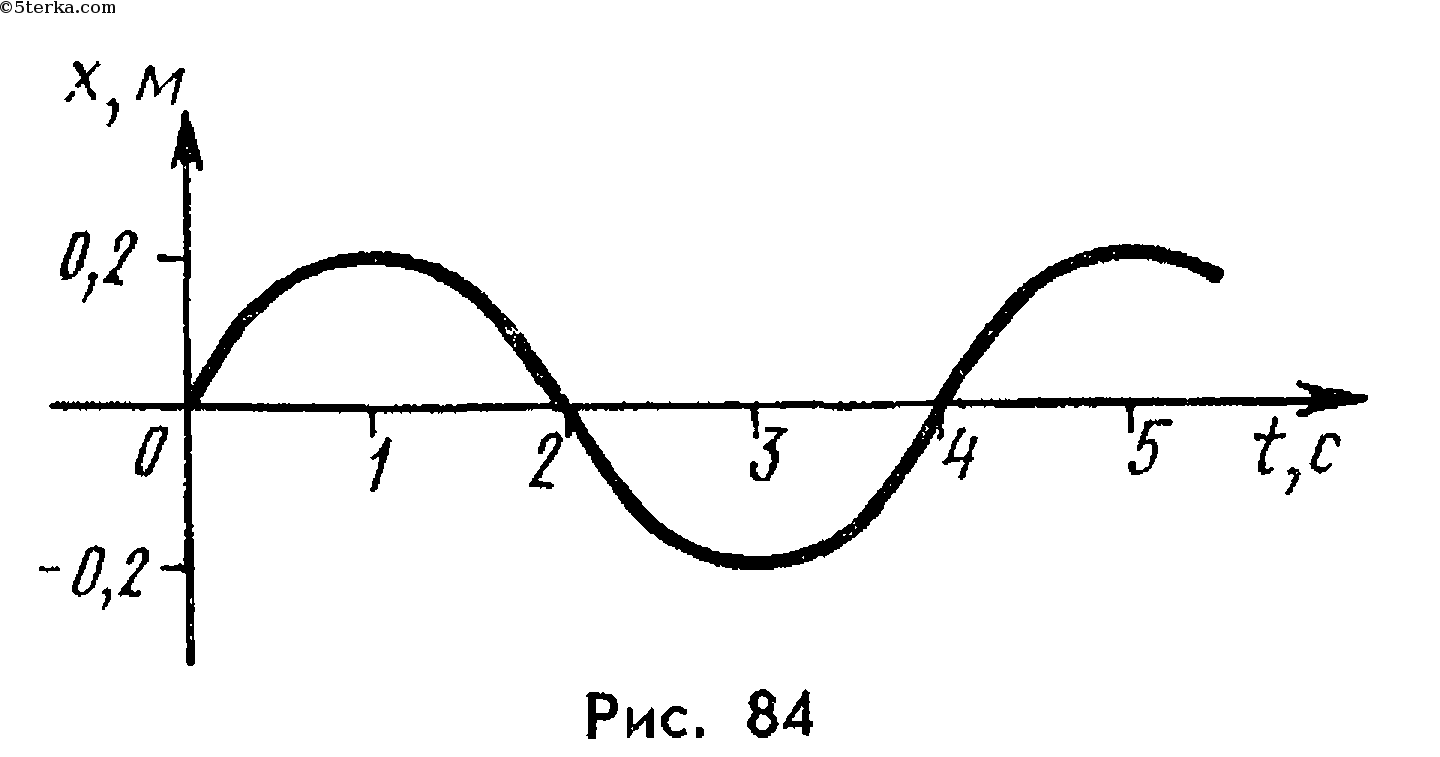
Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимые константы:

x=Asin⁡(θ+ωt),{\displaystyle x=A\sin(\theta _{0}+\omega t),}

где A{\displaystyle A} — амплитуда колебаний маятника, θ{\displaystyle \theta _{0}} — начальная фаза колебаний, ω{\displaystyle \omega } — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями.

Нелинейный маятник

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

sin⁡x2=ϰ⋅sn⁡(ωt;ϰ),{\displaystyle \sin {\frac {x}{2}}=\varkappa \cdot \operatorname {sn} (\omega t;\varkappa ),}

где sn{\displaystyle \operatorname {sn} } — это синус Якоби. Для ϰ<1{\displaystyle \varkappa <1} он является периодической функцией, при малых ϰ{\displaystyle \varkappa } совпадает с обычным тригонометрическим синусом.

Параметр ϰ{\displaystyle \varkappa } определяется выражением

ϰ=ε+ω22ω2,{\displaystyle \varkappa ={\frac {\varepsilon +\omega ^{2}}{2\omega ^{2}}},}

где ε=EmL2{\displaystyle \varepsilon ={\frac {E}{mL^{2}}}} — энергия маятника в единицах t−2.

Период колебаний нелинейного маятника составляет

T=2πΩ,Ω=π2ωK(ϰ),{\displaystyle T={\frac {2\pi }{\Omega }},\quad \Omega ={\frac {\pi }{2}}{\frac {\omega }{K(\varkappa )}},}

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

T=T{1+(12)2sin2⁡(α2)+(1⋅32⋅4)2sin4⁡(α2)+⋯+(2n−1)!!(2n)!!2sin2n⁡(α2)+…}{\displaystyle T=T_{0}\left\{1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\alpha }{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\alpha }{2}}\right)+\dots +\left^{2}\sin ^{2n}\left({\frac {\alpha }{2}}\right)+\dots \right\}},

где T=2πLg{\displaystyle T_{0}=2\pi {\sqrt {\frac {L}{g}}}} — период малых колебаний, α{\displaystyle \alpha } — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

T=T(1+14sin2⁡(α2)).{\displaystyle T=T_{0}\left(1+{\frac {1}{4}}\sin ^{2}\left({\frac {\alpha }{2}}\right)\right).}

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года:

T=2πM(cos⁡(θ2))Lg,{\displaystyle T={\frac {2\pi }{M{\big (}\cos(\theta _{0}/2){\big )}}}{\sqrt {\frac {L}{g}}},}

где M(x){\displaystyle M(x)} — арифметико-геометрическое среднее чисел 1 и x{\displaystyle x}.

Движение по сепаратрисе

Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.

Превращение энергии при гармонических колебаниях

При гармонических
колебаниях пружинного маятника
проис­ходят превращения потенциальной
энергии упруго деформированного телав его кинетическую энергию,
гдеk – коэффициент
упругости,х — модуль смещения
маятника из поло­жения равновесия,m— масса маятника,v—
его скорость. В соот­ветствии с
уравнением гармонических колебаний:

,.

Полная энергия
пружинного маятника:

.

Полная энергия для математического
маятника:

В случае математического
маятника

Превращения энергии при
колебаниях пружинного маятника происходи
в соответствии с законом сохранения
механической энергии ().
При движении маятника вниз или вверх
от положения равновесия его потенциальная
энергия увеличивается, а кинетическая
— уменьшается. Когда маятник проходит
положение равно­весия (х
= 0), его потенциальная
энергия равна нулю и кинетическая
энергия маятника имеет наибольшее
значение, равное его полной энергии.

Таким
образом, в процессе свободных колебаний
маятника его потенциальная энергия
превращается в кинетическую, кинетическая
в потенциальную, потенциальная затем
снова в кинетическую и т. д. Но полная
механическая энергия при этом остается
неизменной.

Вынужденные
колебания. Резонанс.

Колебания, происходящие
под действием внеш­ней периодической
силы, называются вынужден­ными
колебаниями. Внешняя
периодическая си­ла, называемая
вынуждающей, сообщает колеба­тельной
системе дополнительную энергию, которая
идет на восполнение энергетических
потерь, проис­ходящих из-за трения.
Если вынуждающая сила изменяется во
времени по закону синуса или коси­нуса,
то вынужденные колебания будут
гармониче­скими и незатухающими.

В отличие от свободных
колебаний, когда система получает
энергию лишь один раз (при выведении
системы из со­стояния равновесия), в
случае вынужден­ных колебаний система
поглощает эту энергию от источника
внешней периоди­ческой силы непрерывно.
Эта энергия восполняет потери, расходуемые
на пре­одоление трения, и потому полная
энергия колебательной системы no-прежнему
ос­тается неизменной.

Частота вынужденных
колебаний равна часто­те вынуждающей
силы. В случае, когда
частота вынуждающей силы υсовпадает с собственной
ча­стотой колебательной системы υ,происходит рез­кое
возрастание амплитуды вынужденных
колеба­ний — резонанс.
Резонанс возникает
из-за того, что при υ
=υвнешняя сила,
действуя в такт со свободными колебаниями,
все время сонаправлена со скоростью
колеблющегося тела и совершает
по­ложительную работу: энергия
колеблющегося те­ла увеличивается,
и амплитуда его колебаний ста­новится
большой. График зависимости амплитуды
вынужденных колебаний А_тот частоты вынужда­ющей
силы υпредставлен
на рисунке, этот график называется
резонансной кривой:

Явление
резонанса играет большую роль в ря­де
природных, научных и производственных
про­цессов. Например, необходимо
учитывать явление резонанса при
проектировании мостов, зданий и других
сооружений, испытывающих вибрацию под
нагрузкой, в противном случае при
определенных условиях эти сооружения
могут быть разрушены.

Колебания математического маятника

Формула периода колебания математического маятника впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. Будучи современником Исаака Ньютона, Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.

Маятниковые часы Гюйгенса.

Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.

Но вернемся к маятнику, итак, в основе работы маятника лежат его колебания, которые можно выразить формулой, точнее следующим дифференциальным уравнением:

x + w2 sin x = 0

Где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); w – положительная константа, которая определяется из параметров маятника (w = √ g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).

Помимо, собственно колебаний маятник может пребывать и в положении равновесия, при этом сила тяжести, действующая на него, будет уравновешиваться силой натяжения нити. Обычный плоский маятник, пребывающий на нерастяжимой нити, является системой с двумя степенями свободы. Но если, к примеру, нитку заменить на стержень, тогда наш маятник станет системой лишь с одной степенью свободы, так как его движения будут двухмерными, а не трехмерными.

Но если же наш маятник все-таки пребывает на нити и при этом совершает интенсивные колебания вверх-вниз, тогда механическая система приобретает устойчивое положение, именуемое «верх тормашками», еще ее называют маятником Капицы.

Практическое применение математического маятника

Ускорение свободного падения изменяется с географической широтой, поскольку плотность земной коры по всей планете не одинакова. Там, где залегают породы с большей плотностью, оно будет несколько выше. Ускорение математического маятника нередко применяют для геологоразведки. В его помощью ищут различные полезные ископаемые. Просто подсчитав количество колебаний маятника, можно обнаружить в недрах Земли каменный уголь или руду. Это связано с тем, что такие ископаемые имеют плотность и массу больше, чем лежащие под ними рыхлые горные породы.

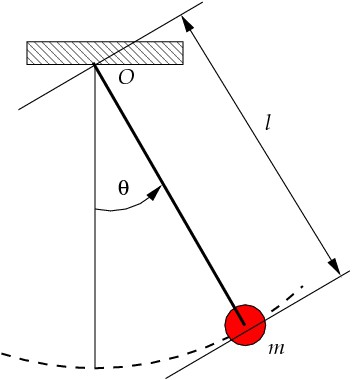
Математическим маятником пользовались такие выдающиеся ученые, как Сократ, Аристотель, Платон, Плутарх, Архимед. Многие из них верили в то, что эта механическая система может влиять на судьбу и жизнь человека. Архимед использовал математический маятник при своих вычислениях. В наше время многие оккультисты и экстрасенсы пользуются этой механической системой для осуществления своих пророчеств или поиска пропавших людей.

Известный французский астроном и естествоиспытатель К. Фламмарион для своих исследований также использовал математический маятник. Он утверждал, что с его помощью ему удалось предсказать открытие новой планеты, появление Тунгусского метеорита и другие важные события. Во время Второй мировой войны в Германии (г. Берлин) работал специализированный Институт маятника. В наши дни подобными исследованиями занят Мюнхенский институт парапсихологии. Свою работу с маятником сотрудники этого заведения называют «радиэстезией».

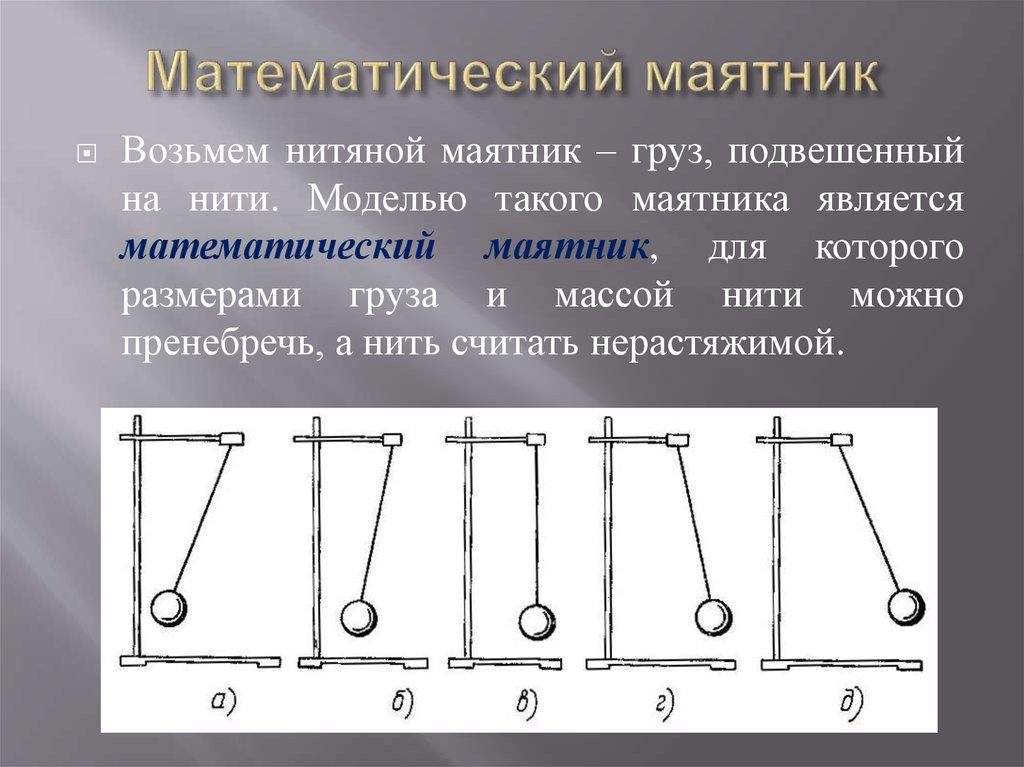
Математический маятник

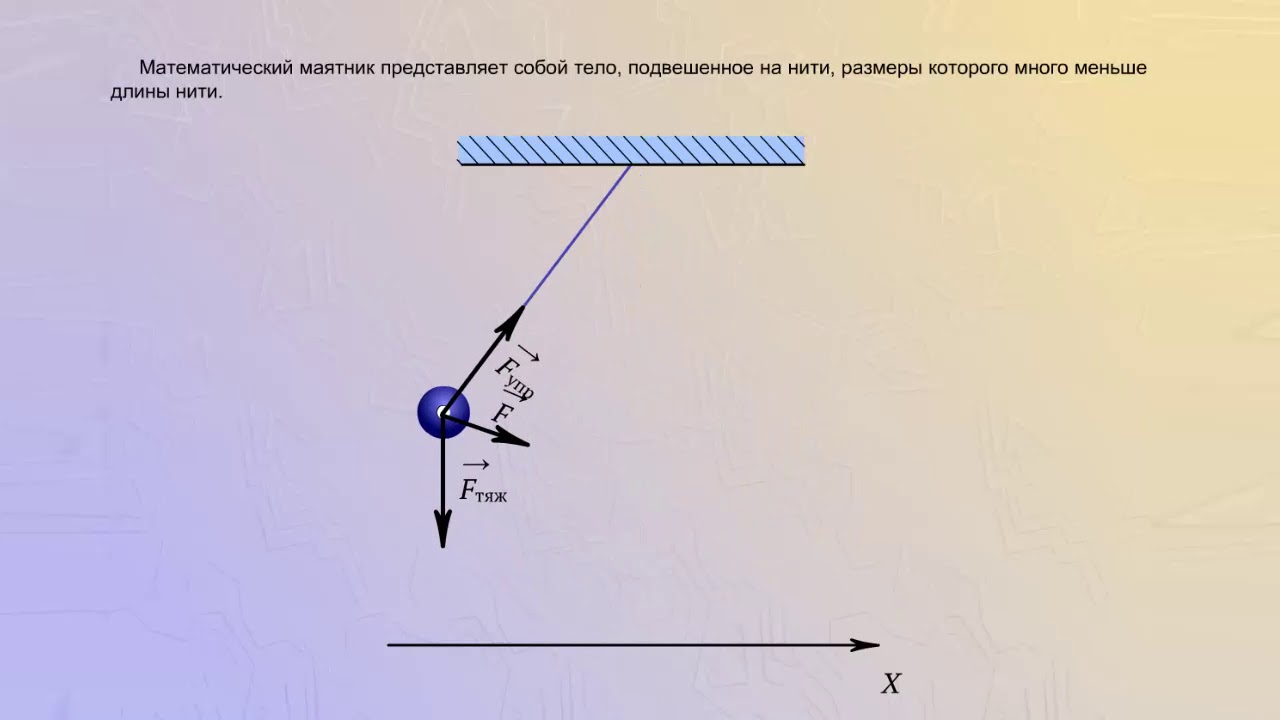
Обычный нитяной маятник представляет собой груз, подвешенный на нити, способный совершать колебательные движения после выведения его из состояния равновесия. Для описания движения такого маятника удобно использовать модель, называемую математическим маятником. Математический маятник имеет следующие отличия от реального маятника.

• Математический маятник, в отличие от реального маятника, не получает и не теряет энергию, трение в математическом маятнике принимается равным нулю.
• Масса математического маятника представляет собой материальную точку, закрепленную на конце нити. Другой конец неподвижен в принятой Системе Отсчета.
• Гравитационное поле, в котором маятник совершает колебания, однородно и направлено в сторону от точки закрепления нити к точке равновесия маятника.
• Нить не имеет веса, и не изменяет свою длину.

Рис. 1. Математический маятник.

Для того, чтобы обычный нитяной маятник хорошо описывался формулами математического маятника, необходимо, чтобы его груз имел малый размер, нить была бы нерастяжимой, и максимальное отклонение маятника было бы намного меньше (более, чем в 10 раз) его длины.

Движение маятника по сепаратрисе

Сепаратрисой называют траекторию динамической системы, у которой двумерное фазовое пространство. Математический маятник движется по ней непериодически. В бесконечно дальнем моменте времени он падает из крайнего верхнего положения в сторону с нулевой скоростью, затем постепенно набирает ее. В конечном итоге он останавливается, вернувшись в исходное положение.

Если амплитуда колебаний маятника приближается к числу π, это говорит о том, что движение на фазовой плоскости приближается к сепаратрисе. В этом случае под действием малой вынуждающей периодической силы механическая система проявляет хаотическое поведение.

При отклонении математического маятника от положения равновесия с некоторым углом φ возникает касательная силы тяжести Fτ = –mg sin φ. Знак «минус» означает, что эта касательная составляющая направляется в противоположную от отклонения маятника сторону. При обозначении через x смещения маятника по дуге окружности с радиусом L его угловое смещение равняется φ = x/L. Второй закон Исаака Ньютона, предназначенный для проекций вектора ускорения и силы, даст искомое значение:

mg τ = Fτ = –mg sin x/L

Исходя из этого соотношения, видно, что этот маятник представляет собой нелинейную систему, поскольку сила, которая стремится вернуть его в положение равновесия, всегда пропорциональна не смещению x, а sin x/L.

Только тогда, когда математический маятник осуществляет малые колебания, он является гармоническим осциллятором. Иными словами, он становится механической системой, способной выполнять гармонические колебания. Такое приближение практически справедливо для углов в 15–20°. Колебания маятника с большими амплитудами не является гармоническим.

Принцип действия математического маятника

А теперь давайте рассмотрим принцип действия математического маятника и узнаем, в чем он заключается.

Принципом действия математического маятника является то, что при отклонении от положения равновесия материальной точки на незначительный угол a, то есть такой угол, при котором бы выполнялось условие sina=a, то на тело будет действовать сила F = -mgsina = -mga.

Мы с вами видим, что сила F имеет отрицательный показатель, а из этого следует, что знак минус говорит нам о том, что данная сила направлена в ту сторону, которая является противоположной смещению. А так как сила F пропорциональна смещению S, то из этого следует, что под действием такой силы материальная точка будет совершать гармонические колебания.