Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
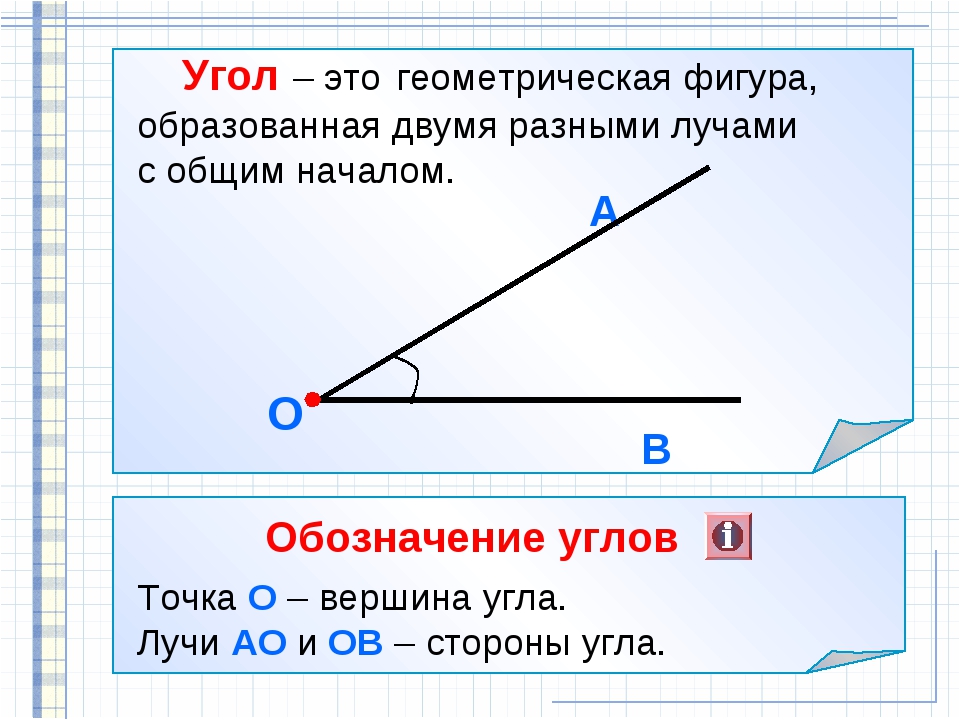
Определение понятий
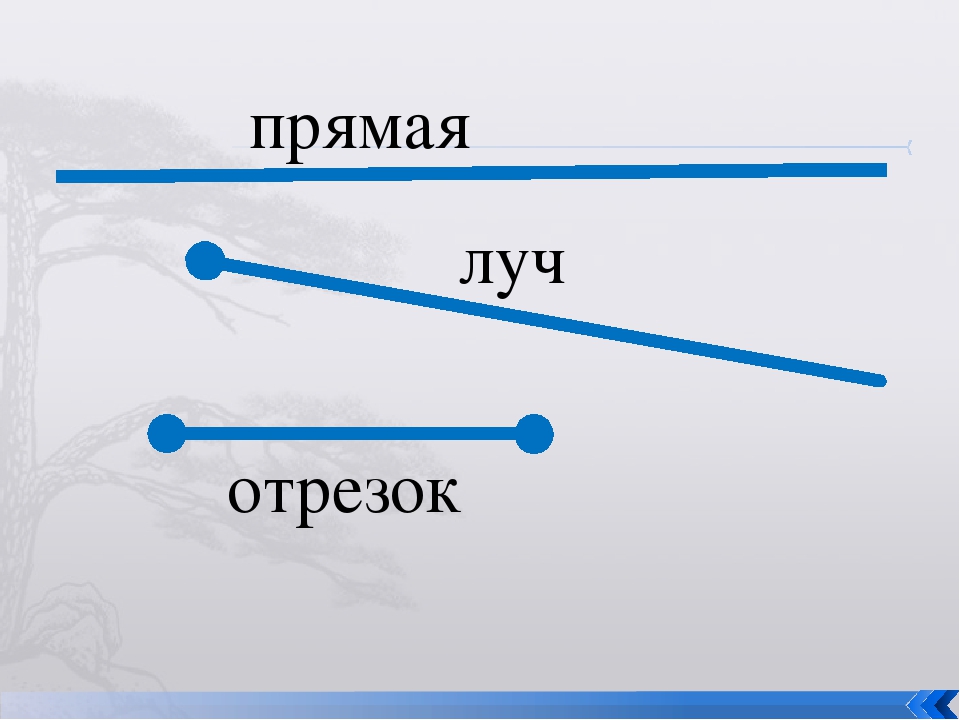
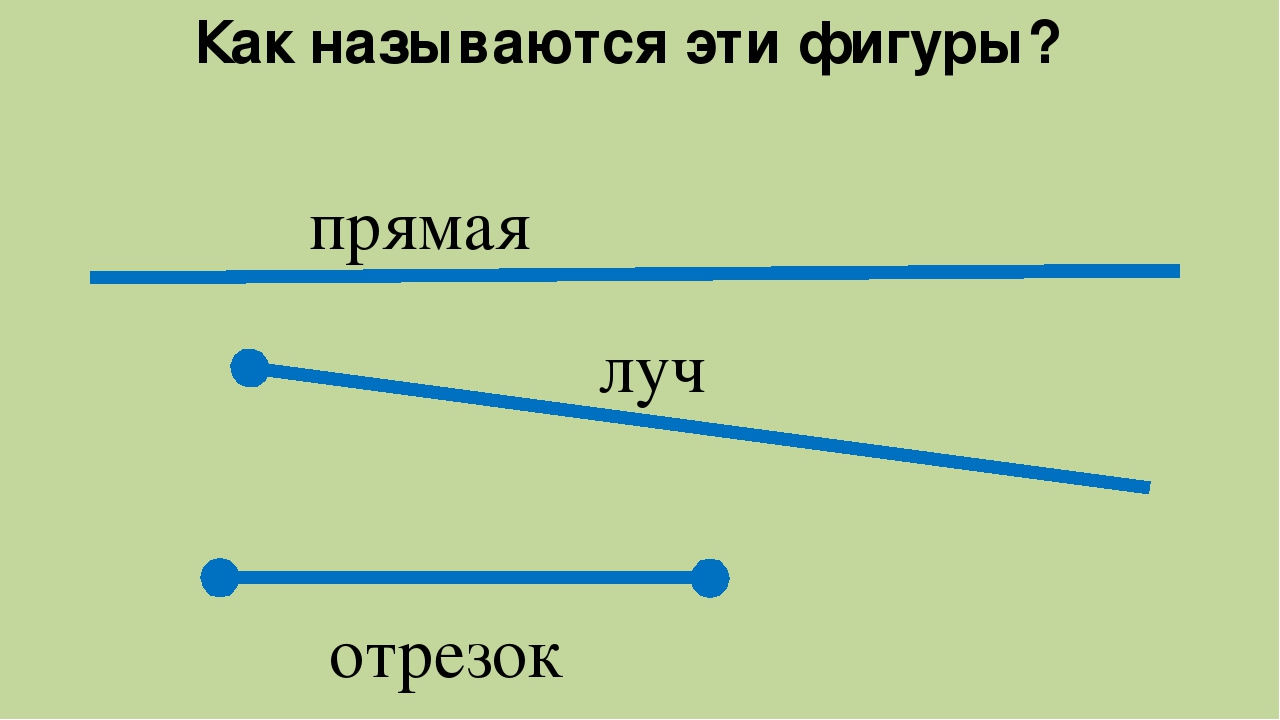
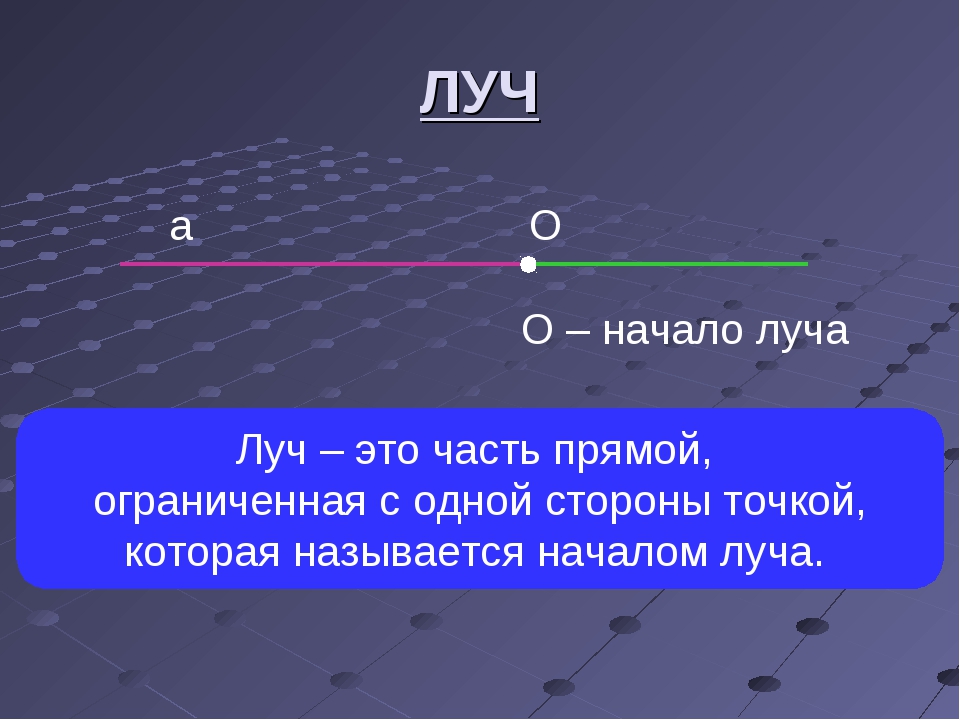
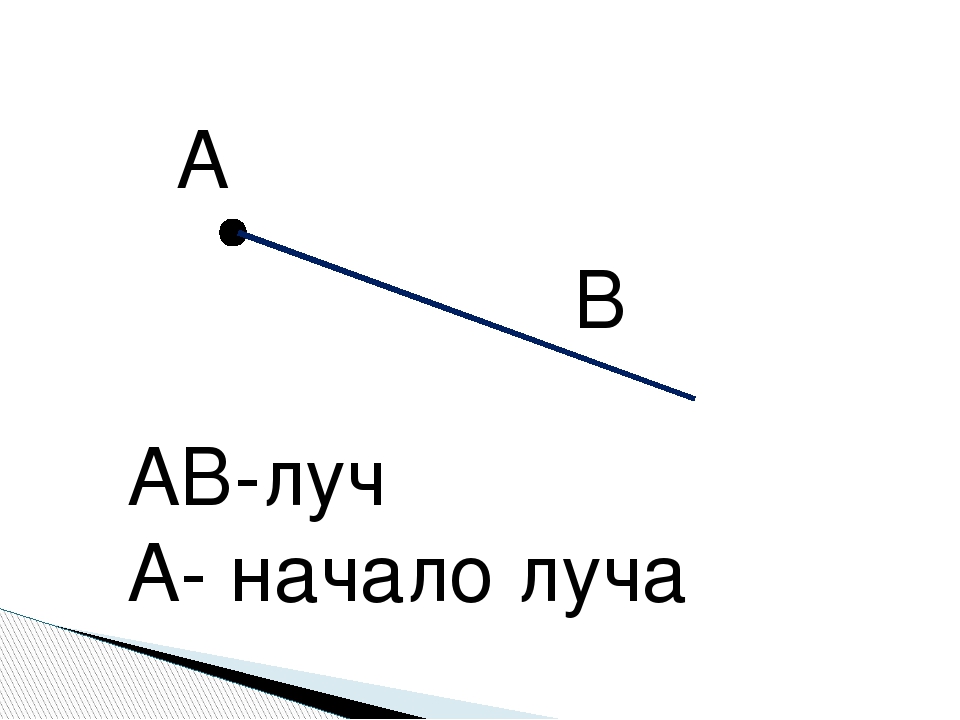
Открытый луч
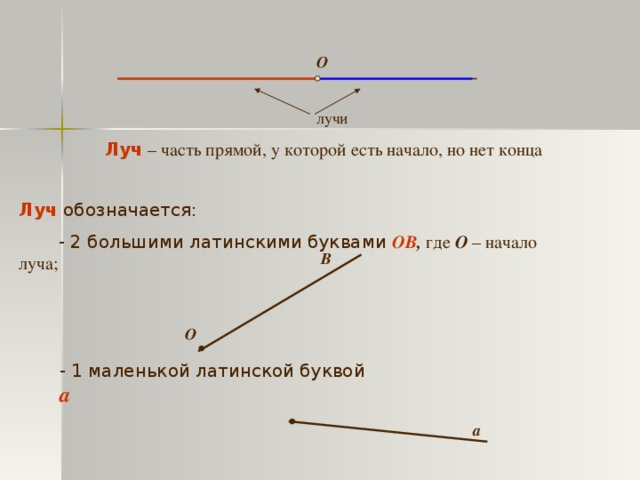
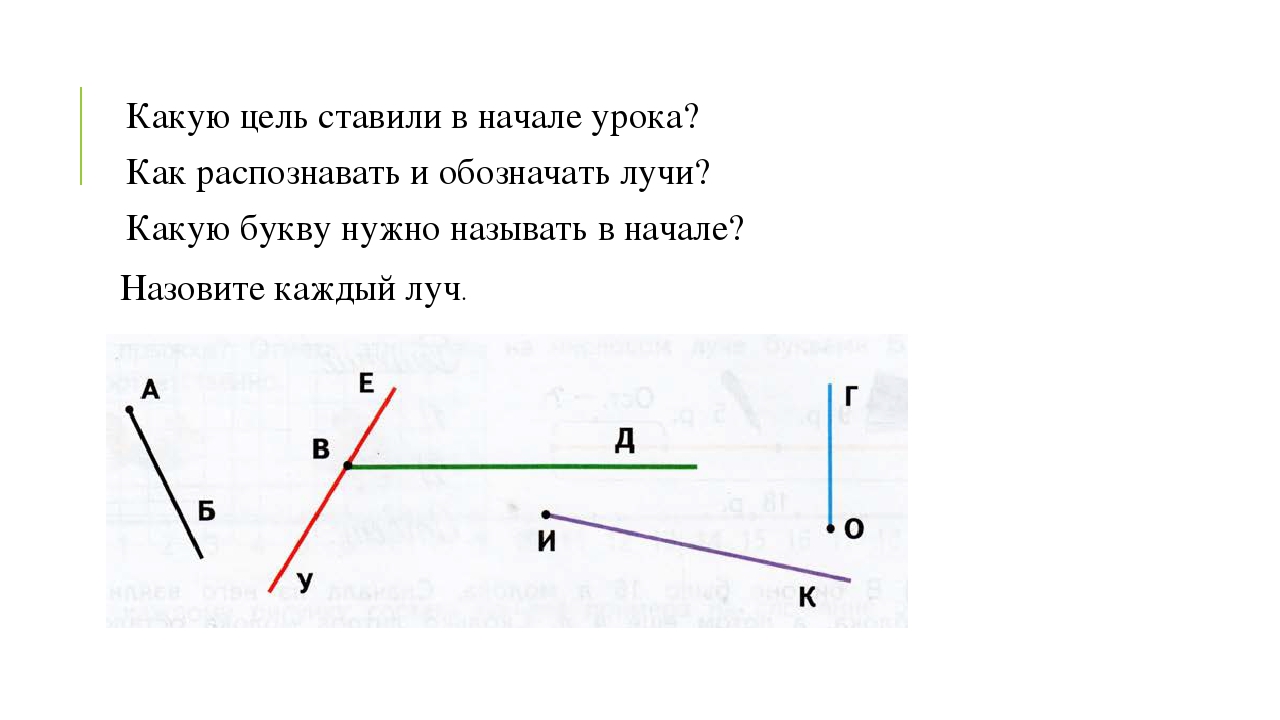
Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
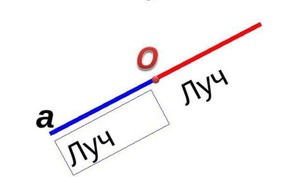
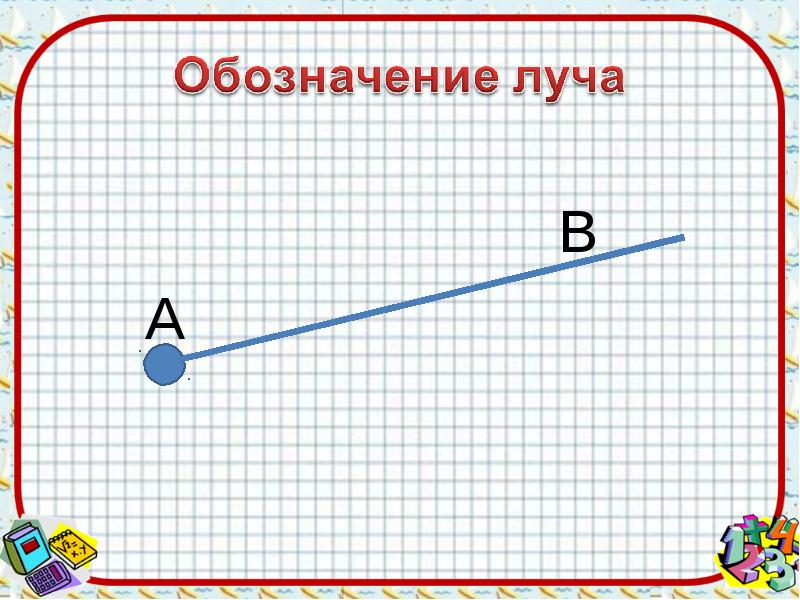
На письме его обычно именуют двумя заглавными (OF)
Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
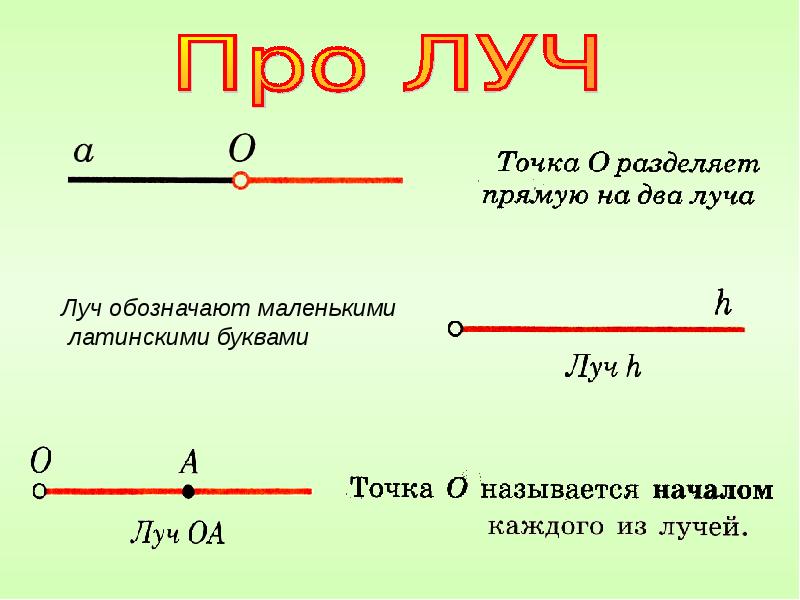
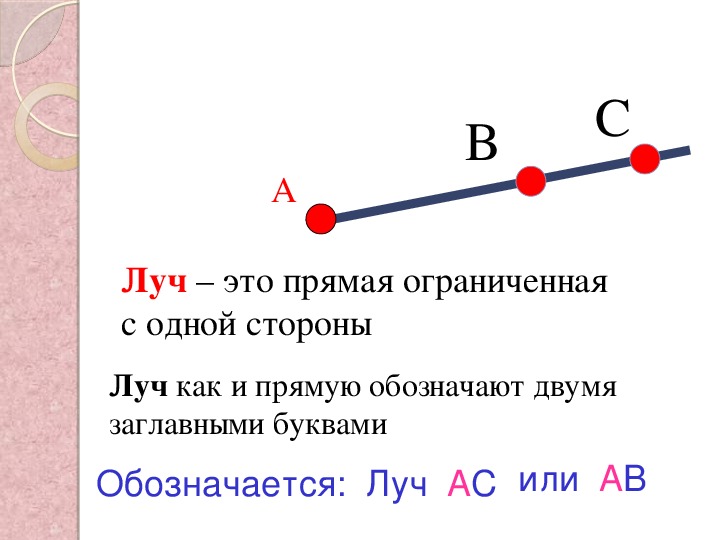
- Попробуйте провести на тетрадном листе линию. Представим, что у вас имеется полупрямая «О». Точка О — исходная, другой быть не может. Это самый распространенный способ.
- Данный метод более интересен: нашу полупрямую возможно назвать не одной буквой. К примеру, на одной линии может быть их две, где первая — начало (буква О), а вторая расположена на каком-то расстоянии. Представим, что на отрезке длиной 10 сантиметров начало названо буквой О, а на расстоянии четырех сантиметров от (О) находится вторая точка (В). Тогда его обозначают «ОВ».
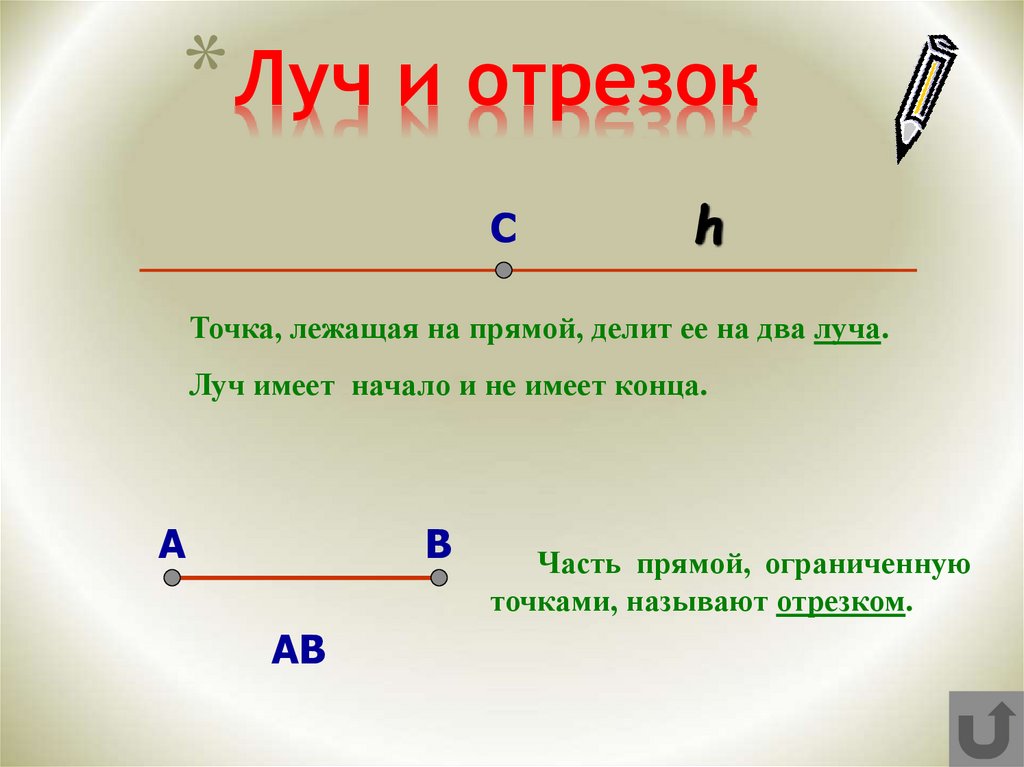
- Третий способ — это когда О у нас располагается не в начале, а с каким-то отступом. Итак, снова начертите прямую с длиной десять сантиметров, отступите слева один сантиметр и отметьте начало. Снова назовите буквой О. В центре точку не ставьте, но обозначьте данную область буквой К. В этот раз буква О — это его начало. Название читается как «ОК»:
- Для начала начертим дополняющие лучи. Как мы уже разобрались, на прямой нужно поставить точку (называем ее О), она производная и разделяет ее на 2 линии, которые пересечься не могут.
- Перейдем к следующему этапу. Теперь нам нужно начертить продолжение — линию, имеющую общее начало с основополагающей, но не совпадающей с нею. А именно: дополняющая линия не является продолжением.
- Чтоб начертить продолжение, проведем из О прямую, которая не располагается на дополняющих, но имеет с ними одно начало. После того как начертили, отметим на новом луче точку В. ОВ теперь лежит на его продолжении из О.
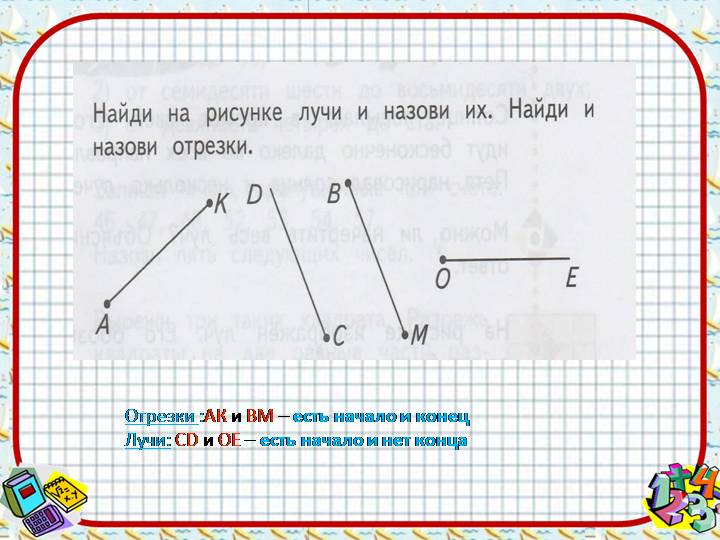
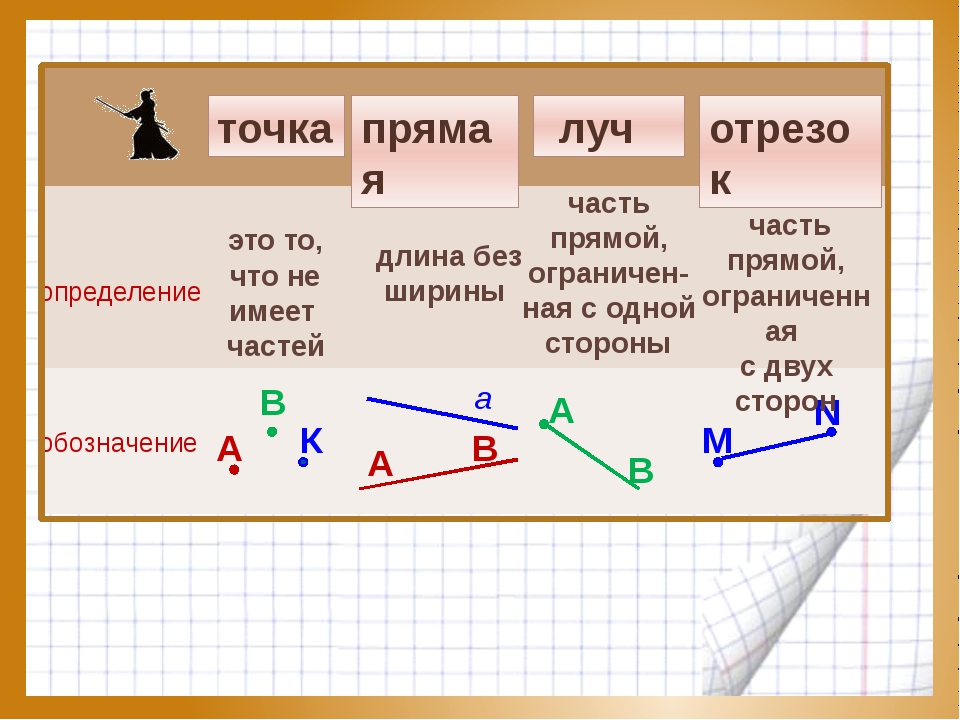
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
- прямой
- ломанной
- кривой
Числовая прямая
Числовая прямая – это луч, с нанесенными на него числами или интервалами чисел. Числовую прямую используют для сравнения дробей, рисунков к задаче и нахождения ОДЗ функции. Последнее встречается чаще всего.
Фигурной скобкой на прямой обозначается область, в которую не могут попадать корни. После решения уравнения, найденные корни наносятся на числовую прямую. Попавшие в фигурную скобку недопустимых значений корни исключаются из решения.

Рис. 3. Числовая прямая.
Что мы узнали?
Мы узнали, что такое луч и числовая прямая. Поговорили о фигурах, составленных из лучей и системах координат, где применяются числовые прямые. Проработали вопрос наглядности изображения нужных точек и разобрались с тем, как правильно проставлять координаты на координатном луче.
Координатные лучи
Еще одно применение лучей это различные системы координат. В математике 5 класса первой темой идет изучение координатной прямой. Это два луча с углом поворота в 180 градусов. Начало лучей обозначается за нулевую точку или начало отчета. Влево от начала отчета откладываются отрицательные координаты, в право-положительные. Другое название координатной прямой: числовой луч.

Рис. 2. Координатный луч.
С помощью координатного луча удобно сравнивать дроби и таким образом решать неравенство.
С помощью координатных лучей создается и координатная плоскость. Так называемая декартова система координат состоит из двух координатных прямых или 4 лучей. Подобная система позволяет определять положение точки на плоскости, вычерчивать графики функций и графически решать разного рода уравнения.
Помимо декартовой системы существует полярная система координат. В полярной системе используются понятия угла и координатной прямой. Координатная прямая определяет положение точки, а угол степень ее подъема над осью.
Полярная система координат одна из самых древних в истории человечества. Так сложилось, что именно пользуясь этой системой, древние мореплаватели покоряли неизвестные просторы нашего мира. Декартова система появилась гораздо позднее. Но она более удобна для ориентации на местности. Декартову систему проще использовать как в разделах математики, так и других дисциплинах: физике, теплотехнике, гидравлике и программировании.
Декартовая система четырьмя лучами делиться на 4 четверти, положение точки в каждой из которых определяется знаком координат. Координаты подразделяют на абсциссы и ординаты. Проще говоря на х и у. Например точка (3, 4) имеет две положительные координаты, а значит она будет находиться в первой четверти. Обе отрицательные координаты соответствуют третьей четверти, положительный у при отрицательном х это вторая четверть, а отрицательный у при положительном х – четвертая.
Чтобы построить точку в декартовых системах координат необходимо от деления числового луча, соответствующего координате, поднять перпендикуляр. Координаты две, значит и перпендикуляров будет два. Точка их пересечения и будет искомой точкой.