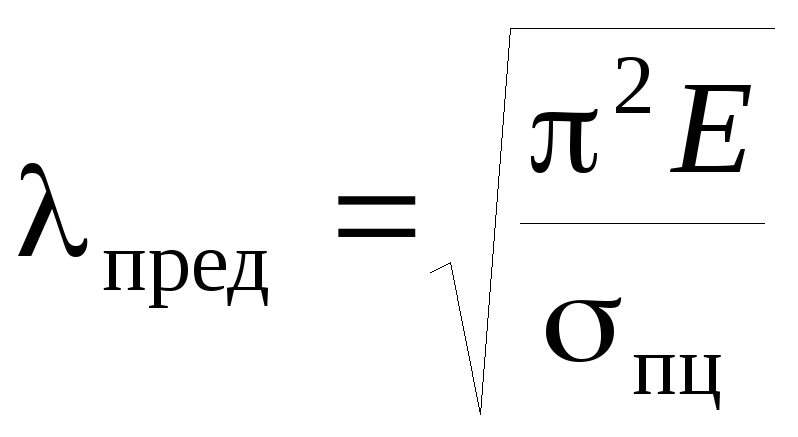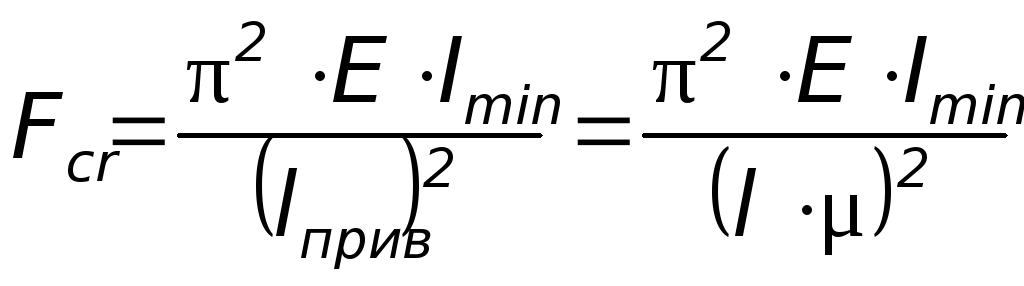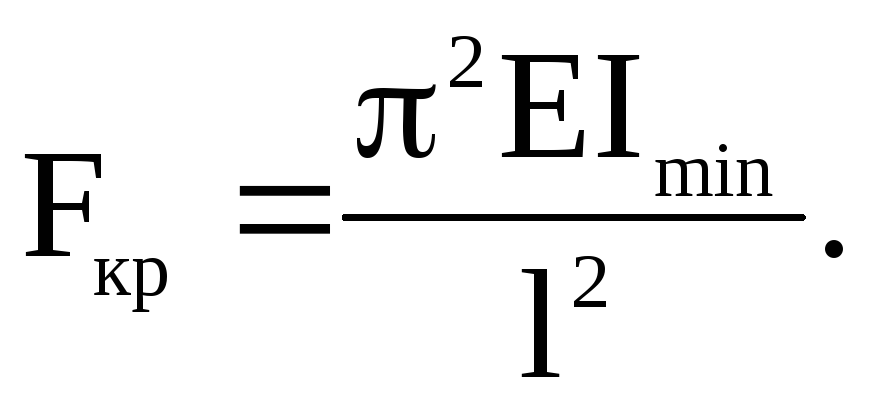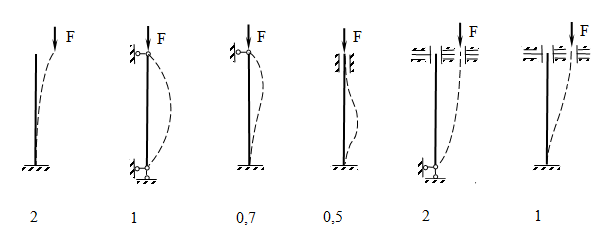ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ. КРИТИЧЕСКАЯ СИЛА
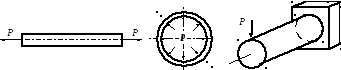
В
этих примерах с увеличением нагрузки
вплоть до разрушения стержень останется
прямым, кольцо – круглым, балка –
изгибаться по одному и тому же уравнению.
Форма равновесия не зависит от величины
внешней силы. Это – устойчивые деформации.
В этих примерах
форма равновесия зависит от величины
силы. Это – неустойчивая форма деформации.
Под
устойчивостью понимают свойство упругой
системы сохранять под нагрузкой
первоначальную форму упругого равновесия.
Потеря
устойчивости наблюдается в элементах
конструкций, работающих на сжатие.
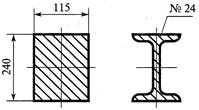
Например, устойчивость может потерять
стенка двутавровой балки при изгибе,
труба, нагруженная внешним давлением,
корпус подводной лодки, корабельный
гребной вал, ходовой винт металлорежущего
станка и т.д.
Остановимся
на изучении наиболее простой формы
потери устойчивости – стержень, сжатый
вдоль продольной оси.
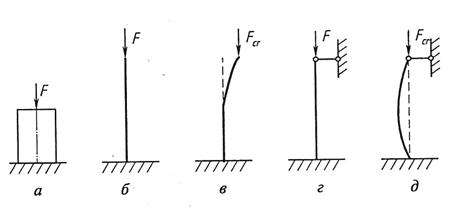
1. Устойчивая форма упругого равновесия.
Стержень, получив малое отклонение,
вновь возвращается в исходное положение.
– механический
аналог
2.
Безразличная форма упругого равновесия.
Стержень, получив малое отклонение,
сохраняет состояние покоя. Сила,
соответствующая безразличному состоянию,
называется критической силой, а напряжения
– критическими напряжениями.
– механический
аналог
3.
Неустойчивая форма равновесия. Стержень,
получив малое отклонение, не возвращается
обратно, а продолжает изгибаться. Прогибы
бытро нарастают, наступает разрушение.
– механический
аналог
Пример
– пшеница . Колос наливается пшеница
полегает.
Сила
Ркр
является опасной нагрузкой. Поэтому
нужно иметь некоторый запас по
устойчивости. Введём понятие допускаемой
силы
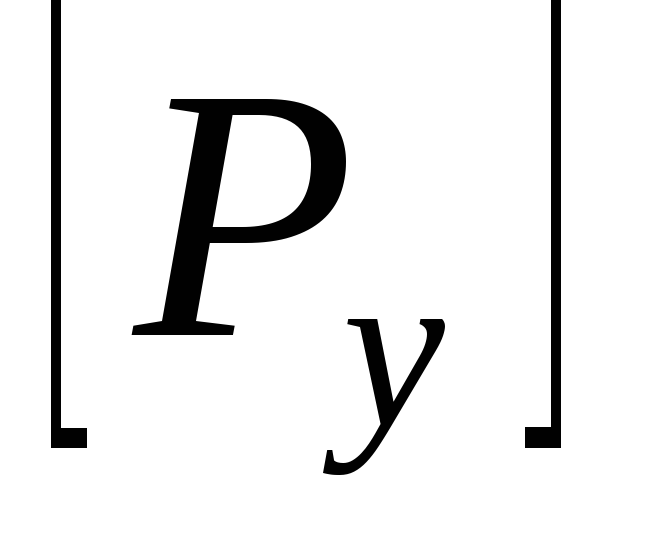
и напряжения. :
:

;
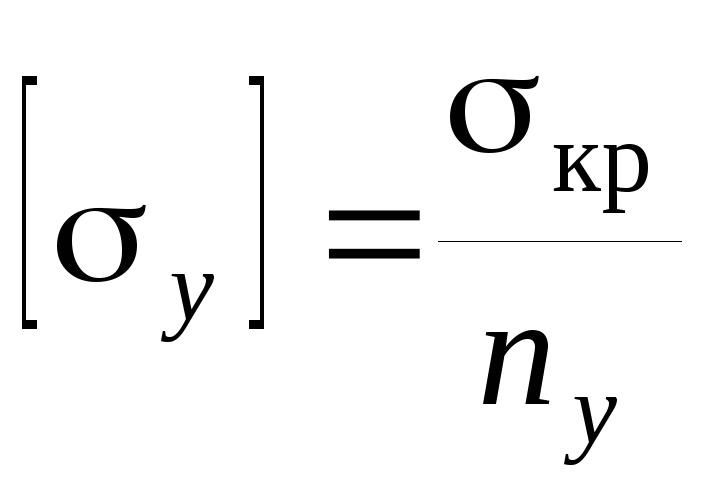
, где

— коэффициент запаса устойчивости.
Обычно
принимают:
для
сталей:

– строительные
конструкции

– машиностроение
для
чугунов

Изгиб стержня,
связанный с потерей устойчивости,
называют продольным изгибом.
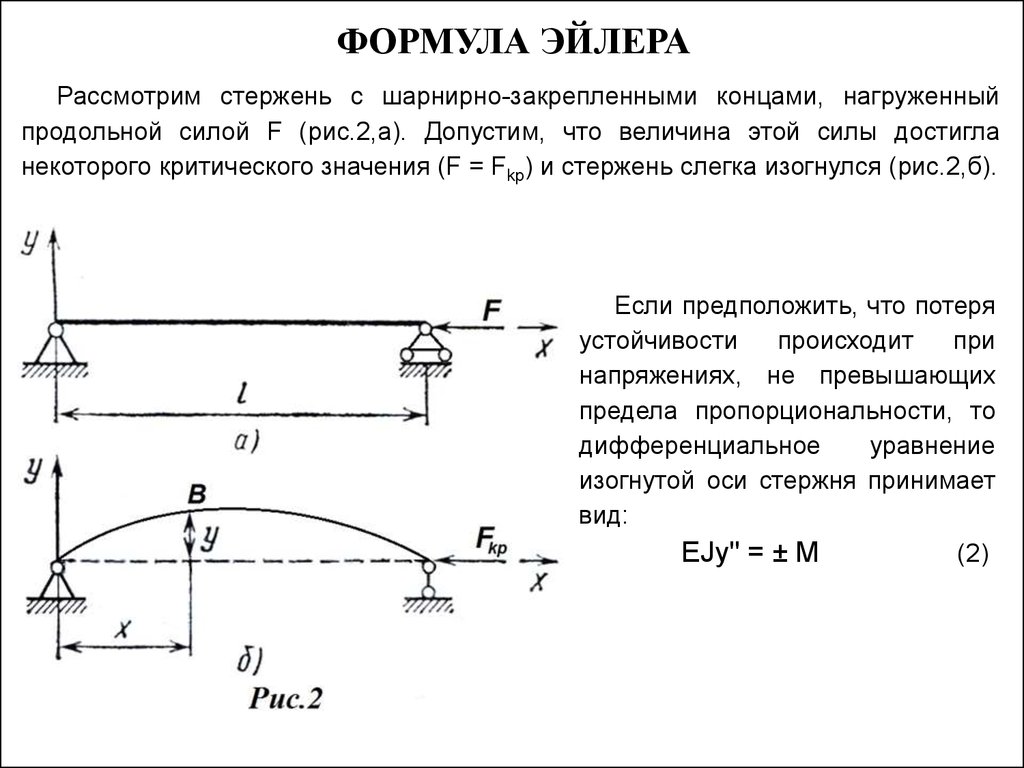
Формула
Л. Эйлера для критической силы (1744 г.)
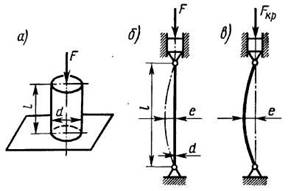
Рассмотрим
стержень длиной l
, на шарнирных опорах сжатый продольной
силой Ркр
.
Доказано,
что упругая линия такого стержня
представляет собой синусоиду.
Величина
силы Ркр
вычисляется по формуле Л. Эйлера (даётся
без вывода)

(1)
где

– наименьший из двух моментов инерции
поперечного сечения стержня.
l
– длина
полуволны синусоиды упругой линии (в
нашем случае – длина стержня).
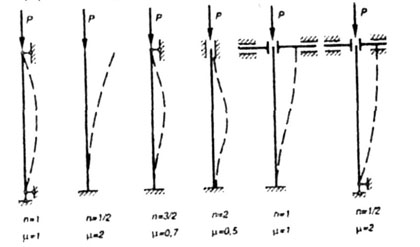
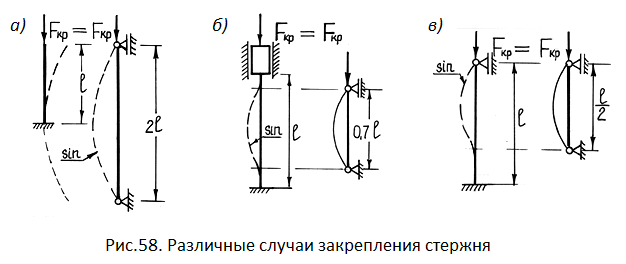
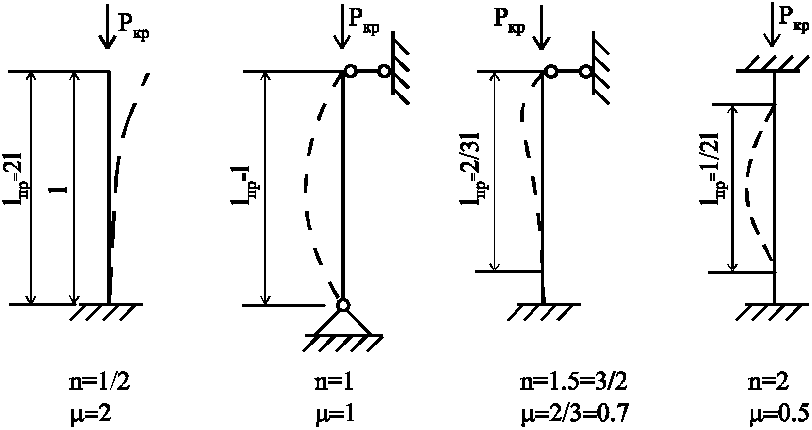
Формулу
(1) можно распространить на другие способы
крепления концов стержня, при которых
длина полуволны будет другой. Тогда
формула Л. Эйлера примет вид:

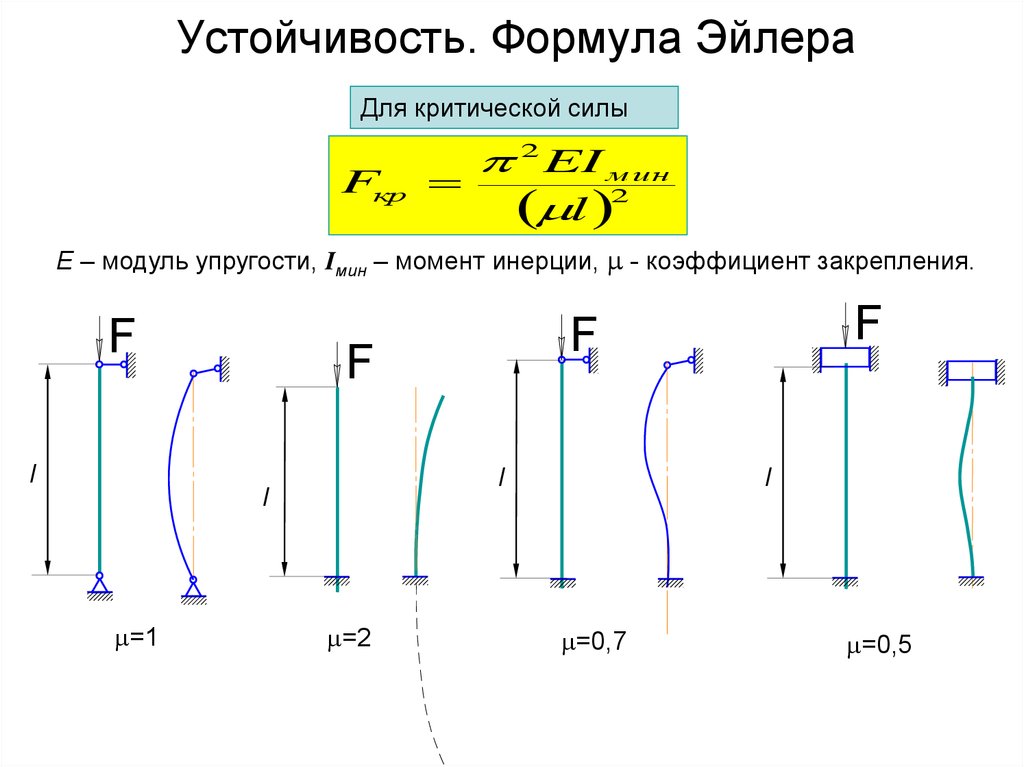
(2)
где
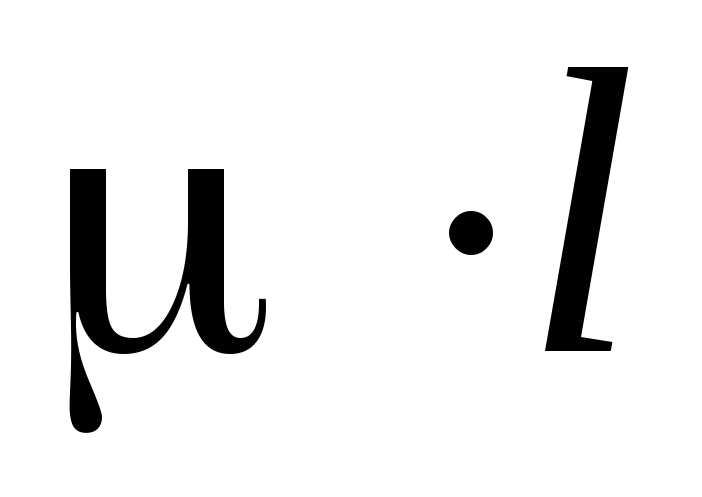
– приведенная длина стержня ;

– коэффициент
приведения длины стержня, зависящий от
способа крепления его концов (введён
Ясинским).

Из
формулы (2) видно, что критическая сила
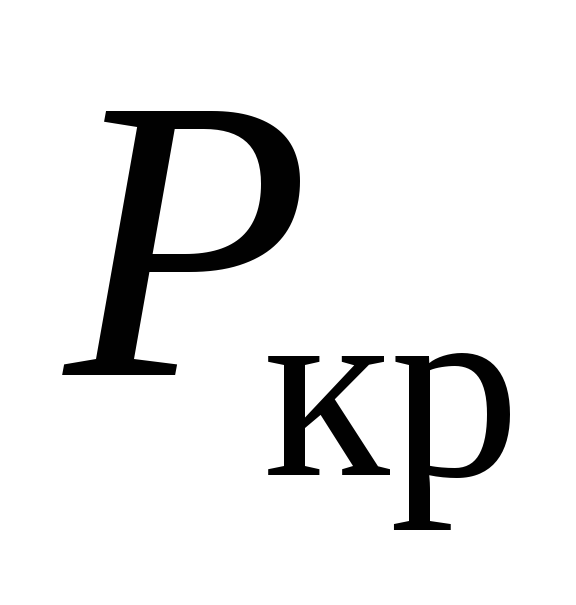
не зависит от характеристик прочности
материала

и
 .
.
Поэтому при большой гибкости стержня,
когда “работает”
формула
Л. Эйлера, не имеет смысла применять
дорогие легированные стали, а наоборот,
следует использовать самые дешёвые
материалы с низкими прочностными
свойствами, т.к.
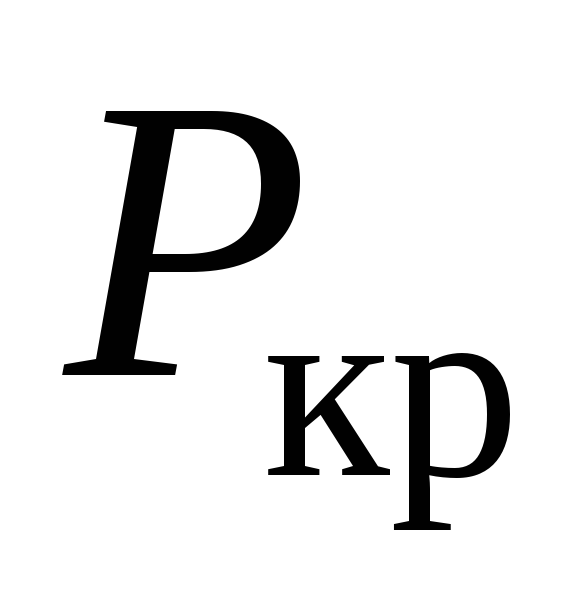
зависит только от модуля Юнга Е,
который для всех сталей примерно одинаков
(Е
= 2·105
МПа).
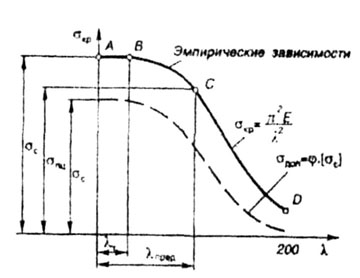
Пределы
применимости формулы Эйлера.
Критические
напряжения по Эйлеру. Гибкость стержня.

– напряжение
от действия
 .
.
Величину

называют минимальным радиусом инерции
сечения.
Обозначим
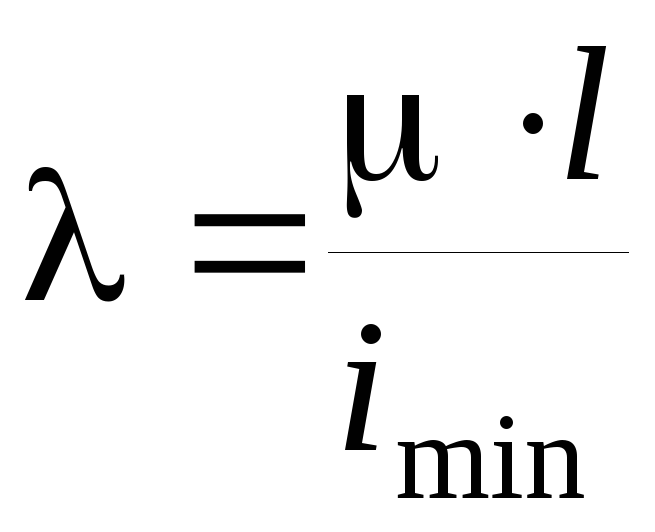
– гибкость стержня.
Тогда
 ,
,
т.е.

(3)
Из
формулы (3) видно, что с уменьшением
гибкости величина
растёт.
Если

достигнет величины

материала стержня, то формула Эйлера
становится неприменимой. Из этого
условия определим значение
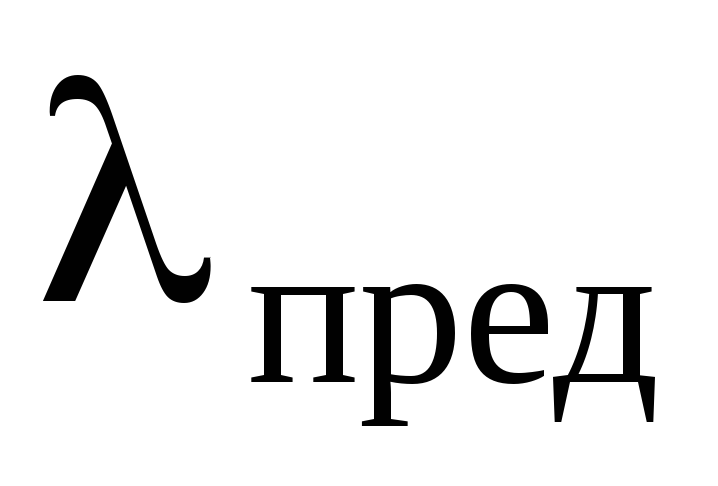 :
: