Правила сравнения чисел
Числа можно сравнивать двумя способами: с помощью натурального ряда и по их десятичной записи.
Правило сравнения с помощью натурального ряда:
Из двух натуральных чисел меньше то, которое в натуральном ряду встречается раньше (т. е. находится левее), и больше то, которое в натуральном ряду встречается позже (т. е. находится правее).
Следовательно, в натуральном ряде каждое число, кроме 1, больше предыдущего.
Пример. Сравним числа 1 и 3, 7 и 4. Запишем все однозначные натуральные числа в одной строке в следующем порядке:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Число 1 меньше числа 3 (1 < 3), так как в натуральном ряду число 1 находится левее числа 3. Число 7 больше числа 4 (7 > 4), так как в натуральном ряду число 7 находится правее числа 4.
Для применения правил сравнения чисел по их десятичной записи необходимо принять одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю.
Правила сравнения натуральных чисел по их десятичной записи:
Если записи сравниваемых чисел состоят из одинакового количества цифр, то числа сравниваются поразрядно слева направо. Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Когда говорят, что цифры равны (или одна цифра больше другой), то имеют ввиду, что соответствующие им числа равны (или одно число больше другого).
Пример. Сравним натуральные числа 4026 и 4019. Для удобства сравнения можно записать их одно под другим:
40264019
Сначала сравниваем значения разряда тысяч. Получаем равенство 4 = 4, поэтому переходим к сравнению значений следующего разряда. Опять получаем равенство 0 = 0, переходим к сравнению значений разряда десятков. Теперь имеем неравенство 2 > 1, из которого делаем вывод, что число 4026 больше числа 4019 (4026 > 4019), потому что у первого числа, цифра разряда десятков (2) больше, чем цифра разряда десятков (1) у второго числа.
Если количество цифр в записи, сравниваемых чисел, разное, то большим будет считаться то число, у которого количество цифр больше.
Пример. Сравним натуральные числа 347 503 и 34 503. Для удобства сравнения можно записать их одно под другим:
| 347 | 503 |
| 34 | 503 |
Записав числа одно под другим, можно наглядно заметить, что первое число имеет большее количество цифр, чем второе, следовательно 347 503 > 34 503.
Два натуральных числа равны, если у них одинаковое количество цифр и цифры одинаковых разрядов равны.
Пример. Сравним числа 38 526 734 и 38 526 734. Для удобства сравнения можно записать их одно под другим:
38 526 73438 526 734
Записи данных чисел одинаковы (количество цифр и цифры одинаковых разрядов равны), следовательно эти числа равны.
Двойные неравенства, тройные неравенства и т. д.
Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.
Пример. Известно, что 4 < 7, а 7 < 16. Эти два неравенства удобнее представить в виде двойного неравенства:
4 < 7 < 16.
Двойные неравенства принято читать с середины. Например, неравенство 2 < 4 < 5 читается так: четыре больше двух, но меньше пяти
.
В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.
Пример. Допустим, нужно сравнить три натуральных числа 11, 34 и 8. Сравнивая данные числа между собой, получим три неравенства 11 < 34, 8 < 11 и 34 > 8, которые можно записать как двойное неравенство:
8 < 11 < 34.
Аналогичным образом строятся тройные, четверные и т. д. неравенства.
Пример. Известно, что 12 < 15, 47 > 15, 47 < 112, тогда можно записать
12 < 15 < 47 < 112.
Равенства и неравенства
Для записи результата сравнения чисел используются следующие знаки:
=, > и <.
При записи сравнения эти знаки располагают между числами.
Первый знак =
называется знаком равенства и заменяет собой слово равно
или равняется
. Например, если числа a и b равны, то пишут a = b и говорят: a равно b
.
Запись, которая состоит из математических выражений, между которыми ставится знак =
называется равенством.
Пример.
4 = 4 — равенство.
2 + 3 = 5 — равенство.
2 + 2 = 1 + 1 + 2 — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).
Равенства могут быть как верными (например, 5 = 5 — верное равенство), так и неверными (например, 11 = 14 — неверное равенство).
Два других знака >
и <
называются знаками неравенства и означают: знак >
— больше
, а знак <
— меньше
. Например, если число a больше числа b, то пишут a > b и говорят: a больше b
или пишут b < a и говорят: b меньше a
.
Знаки >
и <
должны быть обращены остриём к меньшему числу.
Запись, которая состоит из математических выражений, между которыми ставится знак >
или <
называется неравенством.
Пример.
5 > 4 — неравенство.
2 < 7 — неравенство.
2 + 3 < 7 — неравенство (подобные записи представляют собой неравенство двух числовых выражений, и означают неравенство значений этих выражений).
Неравенства могут быть как верными (например, 2 < 9 — верное неравенство), так и неверными (например, 5 > 8 — неверное неравенство).
Кроме неравенств со знаками >
и <
, которые называются строгими, используются нестрогие неравенства, для которых введены знаки ⩾
и ⩽
. Знак ⩾
читается больше или равно
, знак ⩽
— меньше или равно
. Нестрогое неравенство допускает случай равенства левой и правой его частей. Так, например, 7 ⩽ 7 — верное неравенство.
Также для записи неравенства двух натуральных чисел может применяться знак ≠
. Знак ≠
читается не равно
. Например, запись a ≠ b — означает a не равно b.
Обычно, если не оговорено иное, понятие неравенства относится только к записям со знаками >
, <
, ⩾
и ⩽
.
Конспект урока по математике на тему «Задачи на кратное сравнение чисел. Кратное сравнение чисел»
Задачи на кратное сравнение чисел. Кратное сравнение чисел(учебник, с. 41)
Метапредметные (компоненты культурно-компетентностного опыта/приобретенная компетентность): овладеют умениями понимать учебную задачу урока, отвечать на вопросы, обобщать собственные представления; научатся слушать собеседника и вести диалог, оценивать свои достижения на уроке, пользоваться учебником.
Личностные: проявляют мотивацию к учебной деятельности и осознание личностного смысла изучения математики
методы и формы обучения
Методы: словесный, наглядный, практический.
Формы: фронтальная, индивидуальная
Слушают учителя.Демонстрируют готовность к уроку, организуют рабочее место
II. Актуализация знаний
1. Проверка домашнего задания.
Проверяет наличие домашней работы в тетрадях.
Показывают выполненную домашнюю работу.
2. Целеполагание.
Сообщает тему, цель урока.
Внимательно слушают.
3. Устный счет
Математический диктант.
– Увеличьте в 4 раза: 5,3.уменьшите в 4 раза: 32; 26.
Записываю только ответы по цепочке у доски.
Задача 1
Саше 12 лет, а его сестре Лене на 2 года меньше. Сколько лет Лене?
Задача 2
В коробке лежали шарики красного и зеленого цвета. Красных шариков было 9 штук, а зеленых в 8 раз больше. Сколько зеленых шариков лежало в коробке?
Задача 3
У Миши в коллекции 30 зарубежных марок, а российских в 5 раз меньше. Сколько российских марок в коллекции у Миши?
Задача 4
Лена загадала число. Если умножить это число на 8 то получится 64. Какое число загадала Лена?
Выполняют задания
III. Изучение нового материала
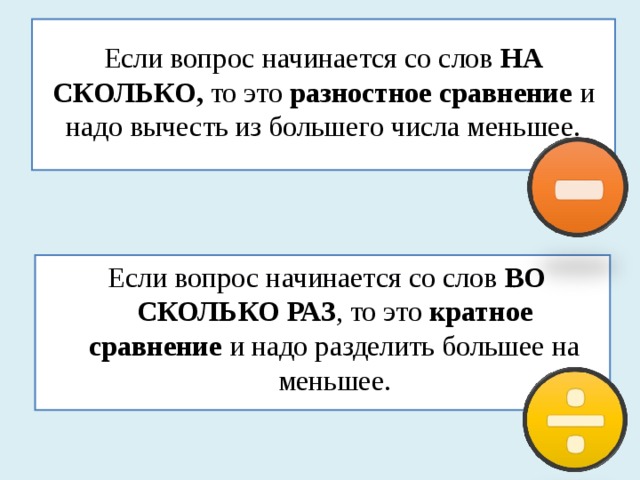
1. Практическая работа: работа над задачами на кратное срав-нение.
Приводит примеры задач на кратное сравнение.
– Положите в первый ряд 12 кружков, во второй – 3 кружка. Как узнать, во сколько раз больше кружков в первом ряду, чем во втором?
– Сколько раз в 12 кружках содержится по 3 кружка?
– Необходимо разделить 12 на 3. В первом ряду
в 4 раза больше кружков, чем во втором, а во втором – в 4 раза меньше, чем в первом
2. Работа со статьей учебника.
– Откройте учебник на с. 41.
Под руководством учителя разбирают объяснение, данное в учебнике.
3. Решение задач.
– Выполните задание № 1.
10 : 2 = 5 (раз).
Ответ: кружков в 5 раз больше, чем квадратов; квадратов в 5 раз меньше, чем кружков.
Физкультминутка
Организует проведение физкультминутки
Выполняют упражнения
IV. Практическая деятельность
-
Самостоятельная работа по карточкам
№ 2.
После чтения можно инсценировать: вызвать к доске 5 девочек и 7 мальчиков и разделить их поровну на две
команды.
1) 5 + 7 = 12 (д.) – всего.
2) 12 : 2 = 6 (д.) – в одной команде.
Ответ: 6 детей в каждой команде.
Приложение1
Составляют краткую запись задачи, записывают решение и ответ.
V. Итоги урока. Рефлексия деятельности
Обобщение полученных на уроке сведений.
Заключительная беседа.
Выставление оценок
– Что сегодня вспомнили, повторили?
– Где можно применить полученные знания?
– Какое значение они имеют для вас?
– Что по этой теме вам кажется непонятным?
Отвечают на вопросы. Делают выводы и обобщения
VI. Домашнее задание
Инструктаж по выполнению домашнего задания
Задают уточняющие вопросы
Вариант-1 (задания из учебника стр.41)
№1. Найди значения выражений.
В детском саду 7 машинок, а кукол в 2 раза больше. Сколько кукол в детском саду.
___________________________________________________________________________________________
Вариант-2 (задания из учебника стр.41)
№1. Найди значения выражений.
Начерти ломаную линию из трёх звеньев. Длина ломаной линии равна 9 см.
Начерти ломаную линию из четырёх звеньев. Длина ломаной линии равна 12 см.
В зоопарке живут 10 обезьян, а тигров в 5 раз меньше. Сколько тигров живут в зоопарке?
______________________________________________________________________________
№1. Найди значения выражений.
х:5=10 146-х= 122 25:х=5 132 +х= 178
Задача 4. Начерти ломаную длина которой вычисляется так: 2*3+4.
-
Моро М.И. Математика. 3 класс. Учеб. для общеобразовательных учреждений с приложением на электронном носителе в 2 ч. Ч. 1. / -М.: Прсвещение,2013, — (Школа России)
-
Компакт – диск Планирование учебной деятельности. Математика. Рабочая программа. Технологические карты уроков. 3 класс. УМК «Школа России». Издательство «Учитель»
-
http://mat-zadachi.ru/increase_reduction.php