Красное смещение

Введение в историю

Как вы догадались, основа лежит в понятии красного смещения. Оно обрело свои очертания ещё в 1870 году, когда было замечено английским математиком и философом Уильямом Клиффордом. Он пришел к выводу, что пространство неодинаково в разных точках, то есть искривлено, а также то, что оно со временем может изменяться. Расстояние между галактиками увеличивается, но координаты остаются прежними. Также его допущения сводились к тому, что это явление каким-то образом относиться к сдвигу материи. Выводы Клиффорда не остались не замеченными и спустя некоторое время легли в основу труда Альберта Эйнштейна под названием «общая теория относительности«.

Промысел

Промышленный лов криля в настоящее время осуществляется в антарктических водах и у побережья Японии; мировая добыча криля в начале XXI века оценивается в 150—200 тыс. тонн.

Промысел ведётся специальными судами — траулерами, которые представляют собой огромные плавучие заводы, на которых выловленный криль может замораживаться, перерабатываться в крилевую муку и/или крилевый жир, а также из него могут производиться Омега-3 капсулы и пищевые добавки.

Сущность явления

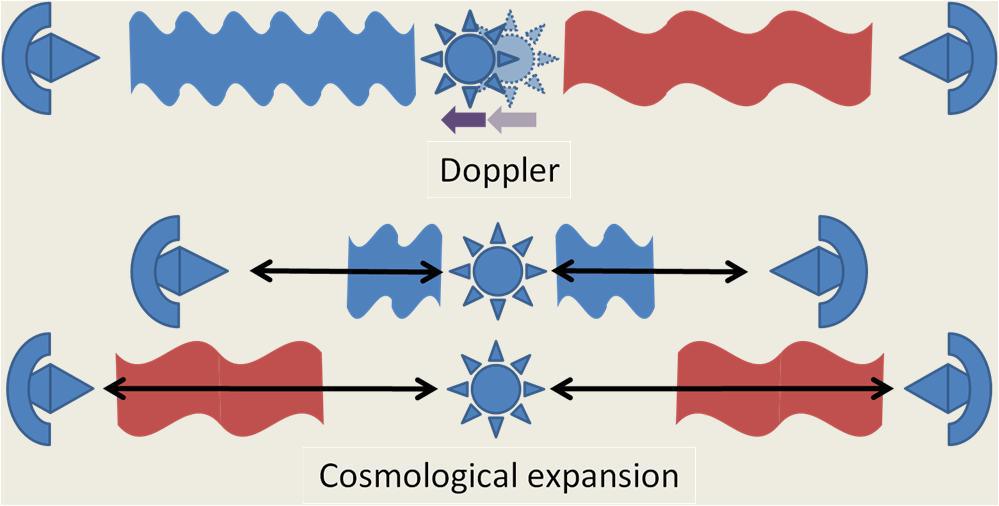
Часто космологическое красное смещение связывают с эффектом Доплера, который связывают с движением галактик друг относительно друга. Однако на самом деле, космологическое красное смещение происходит несколько по-другому, оно связано с расширением пространства согласно ОТО. В наблюдаемое красное смещение от галактик вносит вклад как космологическое красное смещение из-за расширения пространства Вселенной, так и красное или фиолетовое смещения эффекта Доплера вследствие собственного движения галактик. При этом на больших расстояниях вклад космологического красного смещения становится преобладающим.

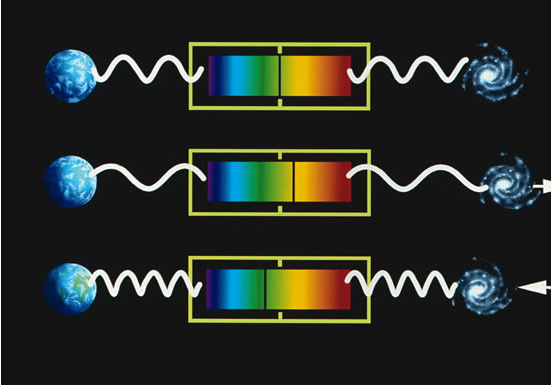
Образование космологического красного смещения можно представить так: рассмотрим свет — электромагнитную волну, идущую от далёкой галактики. В то время как свет летит через космос, пространство расширяется. Вместе с ним расширяется и волновой пакет. Соответственно, изменяется и длина волны. Если за время полёта света пространство расширилось в два раза, то и длина волны и волновой пакет увеличивается в два раза.

Эффект Доплера

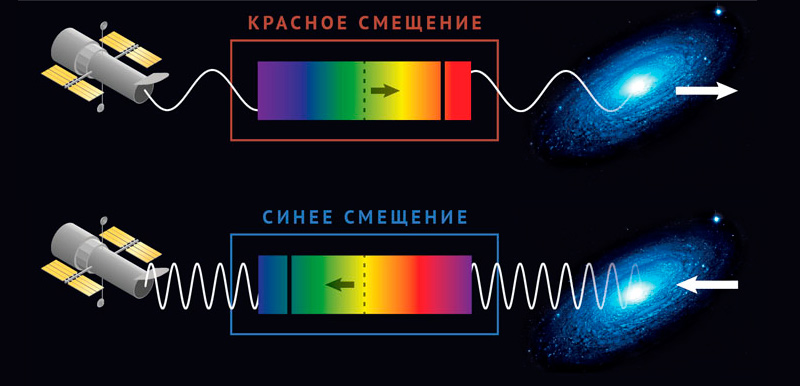
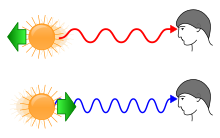
Эффект Доплера — замечательное открытие, во многом определившее дальнейшее развитие физики, — был обнаружен в 1842 году. По преданию, Ньютон открыл закон всемирного тяготения после того, как ему на голову упало яблоко. С открытием эффекта Доплера тоже связана легенда. Якобы оно было сделано в тот момент, когда физик, отдыхая от напряжённых размышлений над волновой теорией, бросал камешки в воду и наблюдал за расходящимися волнами. Суть эффекта проста. Если источник, излучающий волну, приближается к приёмнику (наблюдателю), то последний видит уменьшение длины волны; если источник, наоборот, отдаляется от наблюдателя, то наблюдаемая длина волны увеличивается. Иными словами, если источник света (скажем, звезда) отдаляется от земного наблюдателя, длина световой волны от неё будет увеличиваться, и свет будет казаться наблюдателю красным. Если же звезда будет приближаться к Земле, то свет от неё должен, наоборот, «посинеть» (длина волны синего цвета почти в два раза меньше длины волны красного). Но поскольку голубые и синие звёзды — самые яркие из всех, человеческий глаз воспринимает их цвет как белый (снова Киплинг!). Разумеется, это правило действует не только для световых волн. И звук, и некоторые другие волновые колебания также подчиняются эффекту Доплера. Но, согласитесь, наблюдать действие этого эффекта в мире звёзд гораздо интереснее. Того же мнения придерживался и сам Доплер, опубликовавший в 1842 году работу «О цветном свете двойных звёзд и некоторых других звёзд на небесах». Шестью годами позже другой физик, француз Ипполит Физо подробно описал сдвиг спектральных линий звёзд, находящихся на значительном расстоянии от Солнца, и доказал, что этот сдвиг объясняется эффектом Доплера. Казалось, был найден простой и надёжный способ вычислять и расстояние до далёких звёзд, и скорость, и направление их движения относительно Солнца.

Наблюдение красного смещения

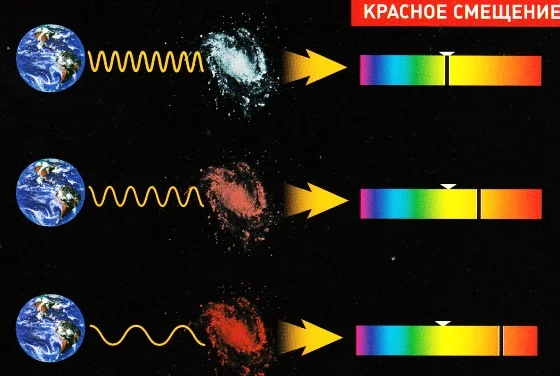
Каждый химический элемент поглощает или излучает электромагнитные волны на строго определённых частотах. Поэтому каждый химический элемент образует в спектре неповторимую картину из линий, используемую в спектральном анализе. В результате эффекта Доплера и/или эффектов ОТО, частота излучения от удалённых объектов, например, звёзд, может изменяться (понижаться или повышаться), а линии соответственно будут смещаться в красную (длинноволновую) или синюю (коротковолновую) часть спектра, сохраняя, однако, своё неповторимое относительное расположение. Смещение линий в красную сторону (обусловленное удалением объекта) и называется «красным смещением».

Расширение пространства

Общепринятая космологическая теория, объясняющая красное смещение, основана на
общей теории относительности. Предполагается, что в однородной и изотропной Вселенной интервал между двумя событиями в сопутствующих координатах имеет следующий вид:

ds2=c2dt2−a2(t)dl2,{\displaystyle ds^{2}=c^{2}dt^{2}-a^{2}(t)dl^{2},}

где c{\displaystyle \textstyle c} — скорость света, а dl2{\displaystyle \textstyle dl^{2}} — элемент квадрата координатного расстояния. В случае плоского пространства он имеет евклидовый вид dl2=dx2+dy2+dz2{\displaystyle \textstyle dl^{2}=dx^{2}+dy^{2}+dz^{2}}. Кроме этого рассматриваются пространства с положительной или отрицательной кривизной. Масштабный фактор a(t){\displaystyle \textstyle a(t)} является (в расширяющейся Вселенной) растущей со временем t{\displaystyle \textstyle t} функцией. Явный вид этой функции определяется уравнениями Эйнштейна и значениями плотности вещества и энергии, которые распределены равномерно в координатах (x,y,z){\displaystyle \textstyle (x,y,z)}. Эти координаты называют сопутствующими, так как предполагается, что вещество в среднем неподвижно относительно этих координат. Образно говоря, каждая частичка вещества является галактикой, «привязанной» к конкретным координатам сопутствующего пространства. При расширении пространства физическое расстояние a(t)dl{\displaystyle \textstyle a(t)dl} между галактиками увеличивается, хотя их сопутствующие координаты остаются неизменными. Наглядно этот процесс можно представить как растяжение «резиновой плёнки» с «приклеенными» к ней галактиками. Для плоского 2-мерного пространства эта плёнка растягивается в плоскости. Моделью сферического 2-мерного пространства является поверхность надувающейся сферы. Для 2-мерных обитателей такой сферы расстояние между всеми галактиками увеличивается во всех точках сферы и нигде нет центра, от которого удаляются галактики.

Ссылки

Доказательства Большого взрыва

Так думают сторонники самой популярной в настоящее время теории возникновения Вселенной — Большого взрыва. У теории Большого взрыва есть два наиболее существенных экспериментальных доказательства — реликтовое излучение (о котором мы уже писали в №23 «Тайн XX века» за 2019 год) и красное смещение в спектрах галактик. В самом деле если всё началось с Большого взрыва, то его последствия в виде космического вещества, объединившиеся со временем в целые звёздные системы, и должны разлетаться во все стороны. А если две галактики разлетаются в разные стороны, их скорость друг относительно друга увеличивается. Они все больше отдаляются друг от друга; появляется и усиливается со временем красное смещение. Можно сказать и по-другому: Вселенная расширяется, и её расширение как бы «относит» сформировавшиеся галактики в разные стороны от некоего центра. Свет, являющийся электромагнитной волной определённой длины (или, как говорят физики, «волновой пакет»), летит сквозь пространство, которое все время увеличивается. Вместе с расширением пространства увеличивается и волновой пакет. Соответственно, изменяется и длина волны света. Если за время полёта света пространство расширилось в два раза, то и волновой пакет становится в два раза длиннее. Так и получается, что синий или фиолетовой свет далёкой (очень-очень далёкой!) от нас галактики, добравшись, наконец, до Млечного Пути, становится красным… или вовсе переходит в невидимую часть спектра. С точки зрения земного человечества очень заманчивой представляется идея, что все галактики разлетаются именно «от нас». То есть мы, наш Млечный Путь, находимся «в центре» мироздания, в том самом месте, где когда-то взорвалось «космическое яйцо». Увы, ни доказательств, ни опровержений этой прекрасной идеи нет; их и не может быть получено до тех пор, пока человечество не овладеет средствами межгалактической связи и не сможет взглянуть на расширяющуюся Вселенную глазами обитателей, скажем, Малого Магелланова облака. Наша ближайшая галактическая соседка — Туманность Андромеды — находится, к сожалению, «слишком близко» от нас, чтобы по красному смещению других разбегающихся галактик определить местоположение исторического Центра Вселенной.

Метки: Тайны 20 века, звезда, галактика, закон, красный, смещение, спектр, Хаббл, эффект, Доплер

Первые обоснованные идеи

Эффект Доплера

Впервые же точные сведения о расширении Вселенной были представлены с помощью астроспектрографии. Когда в Англии, в 1886 году, астрономом-любителем Уильямом Хаггинсом было отмечено, что длины волн звёздного света сдвинуты в сравнении с такими же земными волнами. Такое измерение стало возможным при использовании оптической интерпретации эффекта Доплера, суть которого в том, что скорость звуковых волн постоянна в однородной среде и зависит лишь от свойств самой среды, в таком случае можно вычислить величину вращения звезды. Все эти действия позволяют нам негласно определить движение космического объекта.

Примечания

↑
Doppler, Christian. Beiträge zur fixsternenkunde. — Prague: G. Haase Söhne, 1846. — Т. 69.
O’Connor, John J. . MacTutor History of Mathematics archive. University of St Andrews (1998).
Pannekoek, A. A History of Astronomy. — Dover, 1961. — С. 451. — ISBN 978-0-486-65994-7.
Adams, Walter S. Preliminary catalogue of lines affected in sun-spots (англ.) // Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington : journal. — Contributions from the Solar Observatory of the Carnegie Institution of Washington: Carnegie Institution of Washington, 1908. — Vol. 22. — P. 1—21. — . Reprinted in
Slipher, Vesto. The radial velocity of the Andromeda Nebula // Lowell Observatory Bulletin. — 1912. — Т. 1. — С. 2.56—2.57. — .
Slipher, Vesto. Spectrographic Observations of Nebulae (англ.) // Popular Astronomy. — 1915. — Vol. 23. — P. 21—24. — .
English translation in )
This was recognized early on by physicists and astronomers working in cosmology in the 1930s. The earliest layman publication describing the details of this correspondence is (Reprint: ISBN 978-0-521-34976-5)

Определение

Гравитационное красное смещение принято обозначать символом zG{\displaystyle z_{G}} :

zG=λ−λλ=ν−νν{\displaystyle z_{G}={\frac {\lambda -\lambda _{0}}{\lambda _{0}}}={\frac {\nu _{0}-\nu }{\nu }}} ,

где:

ν{\displaystyle \nu } и λ{\displaystyle \lambda } — измеренная частота и длина волны фотона,

ν{\displaystyle \nu _{0}} и λ{\displaystyle \lambda _{0}} — лабораторная частота и длина волны фотона.

Гравитационное красное смещение было предсказано А. Эйнштейном (1911) при разработке общей теории относительности (ОТО), и в слабых гравитационных полях приблизительно равно

zG=φ−φc2=GMc2r−GMc2R{\displaystyle z_{G}={\frac {\varphi -\varphi _{0}}{c^{2}}}={\frac {GM}{c^{2}r}}-{\frac {GM}{c^{2}R}}} ,

где:

zG{\displaystyle z_{G}} — относительное смещение спектральных линий под влиянием гравитации,

φ=−GMR{\displaystyle \varphi =-{\frac {GM}{R}}} и φ=−GMr{\displaystyle \varphi _{0}=-{\frac {GM}{r}}} — значения гравитационного потенциала в точках наблюдения и излучения соответственно,

G{\displaystyle G} — гравитационная постоянная Ньютона;

M{\displaystyle M} — масса гравитирующего тела,

c{\displaystyle c} — скорость света,

r{\displaystyle r} — радиальное расстояние от центра масс тела до точки излучения,

R{\displaystyle R} — радиальное расстояние от центра масс тела до точки наблюдения.

Для света, излучаемого на расстоянии r{\displaystyle r} от центра масс массивного тела и принимаемого на бесконечности (R=∞{\displaystyle R=\infty }), гравитационное красное смещение приблизительно равно:

zG=GMc2r.{\displaystyle z_{G}={\frac {GM}{c^{2}r}}.}

Поскольку первая космическая скорость на расстоянии r{\displaystyle r} от тела массой M{\displaystyle M} равна

VI=GMr,{\displaystyle V_{I}={\sqrt {\frac {GM}{r}}},} то формула для красного смещения может принять следующий вид:

zG=VI2c2.{\displaystyle z_{G}={\frac {V_{I}^{2}}{c^{2}}}.}

Универсальная формула для изменения частоты, приложимая в любой
метрической теории гравитации в условиях применимости приближения геометрической оптики (эйконала):

νrνe=sesr=u→r⋅k→ru→e⋅k→e,{\displaystyle {\frac {\nu _{r}}{\nu _{e}}}={\frac {s_{e}}{s_{r}}}={\frac {{\vec {u}}_{r}\cdot {\vec {k}}_{r}}{{\vec {u}}_{e}\cdot {\vec {k}}_{e}}},}

где

νr{\displaystyle \nu _{r}} и νe{\displaystyle \nu _{e}} — частоты принятого (recieved) и излучённого (emitted) сигнала, соответственно,

sr{\displaystyle s_{r}} и se{\displaystyle s_{e}} — собственные времена колебаний,

ur{\displaystyle u_{r}} и ue{\displaystyle u_{e}} — 4-скорости приёмника и источника, а

kr{\displaystyle k_{r}} и ke{\displaystyle k_{e}} представляют собой касательный светоподобный вектор (волновой 4-вектор сигнала), параллельно перенесённый вдоль траектории распространения сигнала.

2.1 Фотон-нейтринные взаимодействия

Согласно полевой теории элементарных частиц электронное нейтрино (как и любая другая элементарная частица) обладает постоянным электрическим и магнитным полем и переменным электромагнитным полем. Согласно классической электродинамики данные электромагнитные поля будут взаимодействовать с другими электромагнитными полями, в том числе и с электромагнитным полем фотона. Таким образом, прохождение фотона через электронное нейтрино (выбрасываемое в гигантских количествах звездами) или его молекулярное соединение (ν_e₂) не окажется для последнего не замеченным — пусть это будет очень слабое изменение или уменьшение энергии фотона, но оно будет. И чем больше фотон повстречает на своем пути электронных нейтрино или их молекулярных соединений — тем больше энергии он потеряет и соответственно сильнее будет красное смещение.

Одно дело, когда фотон летит параллельно с электронным нейтрино (движущейся с около световой скоростью) одним курсом, когда они были оба излучены солнцем и совсем другое дело, когда фотон сталкивается с покоящимся электронным нейтрино, со связанным состоянием из двух электронных нейтрино (ν_e₂), или с электронным нейтрино, выпущенным другой звездой (движущейся в другом направлении). Теряемая фотоном энергия от взаимодействия с электронным нейтрино зависит от ориентации спина электронного нейтрино, траектории по которой фотон проходит через электронное нейтрино, а также от энергии самого фотона. Это не просто посчитать, но можно измерить с помощью космических аппаратов и лазеров.

Необходимо отметить, что данное взаимодействие не соответствует стандартной модели, поскольку последняя наделяет участвующие в нем элементарные частицы разными типами фундаментальных взаимодействий (в рамках модели):

нейтрино — гипотетическим слабым взаимодействием,
фотон — электромагнитным взаимодействием.

Поэтому и делается вывод о разбегании галактик на одностороннем толковании красного смещения в пользу эффекта Доплера. — В противовес этому полевая теория элементарных частиц установила о наличии электромагнитных полей у всех элементарных частиц, в том числе и у такой неуловимой элементарной частицы как у электронного нейтрино. Следовательно, фотон и электронное нейтрино обладая общими электромагнитными взаимодействиями, согласно классической электродинамике должны взаимодействовать друг с другом и у гипотезы «старения света» появляется союзник — полевая теория элементарных частиц. И если отбросить стандартную модель (модель сказочных кварков, сказочных глюонов, и вымышленных, в добавку к существующим, фундаментальных взаимодействий) ошибочность, которой уже доказана, то это автоматически низвергает и «теорию Большого взрыва» до уровня простой гипотезы, противоречащей законам природы.

Параметр красного смещения

При описании эффекта космологического красного смещения удобно от физического времени t{\displaystyle \textstyle t} перейти к координатному η{\displaystyle \textstyle \eta }, определяемому соотношением dη=dta(t){\displaystyle \textstyle d\eta =dt/a(t)}. Тогда в одномерном случае можно записать:

ds2=c2dt2−a2(t)dχ2=a2(t)(c2dη2−dχ2),{\displaystyle ds^{2}=c^{2}dt^{2}-a^{2}(t)\,d\chi ^{2}=a^{2}(t)(c^{2}d\eta ^{2}-d\chi ^{2}),}

где χ{\displaystyle \textstyle \chi } — радиальная координата сопутствующего пространства в направлении источника. Распространению световых сигналов соответствует случай нулевого интервала ds={\displaystyle \textstyle ds=0} или dχ=±cdη{\displaystyle \textstyle d\chi =\pm c\,d\eta }. Поэтому в координатных величинах (η,χ){\displaystyle \textstyle (\eta ,\chi )} траектория светового сигнала линейна χ=±cη+const{\displaystyle \textstyle \chi =\pm c\,\eta +const}. Пусть удалённый источник, расположенный в координате χ{\displaystyle \textstyle \chi }, в момент времени t{\displaystyle \textstyle t} в прошлом испускает два последовательных сигнала с промежутком Δη{\displaystyle \textstyle \Delta \eta }. В начало координат χ={\displaystyle \textstyle \chi =0}, в котором находится наблюдатель, эти сигналы приходят в настоящий момент времени t{\displaystyle \textstyle t_{0}}. В силу линейности траектории промежуток координатного времени между ними будет таким же, как и при испускании Δη=Δη{\displaystyle \textstyle \Delta \eta _{0}=\Delta \eta }. Возвращаясь к физическим интервалам времени это соотношение можно записать следующим образом:

Δta(t)=Δta(t).{\displaystyle {\frac {\Delta t_{0}}{a(t_{0})}}={\frac {\Delta t}{a(t)}}.}

Считая, что каждый сигнал является максимумом периодической электромагнитной волны с
частотой ν=1Δt{\displaystyle \textstyle \nu =1/\Delta t} и длиной волны λ=cν{\displaystyle \textstyle \lambda =c/\nu }, можно записать:

1+z=a(t)a(t)=νν=λλ.{\displaystyle 1+z={\frac {a(t_{0})}{a(t)}}={\frac {\nu }{\nu _{0}}}={\frac {\lambda _{0}}{\lambda }}.}

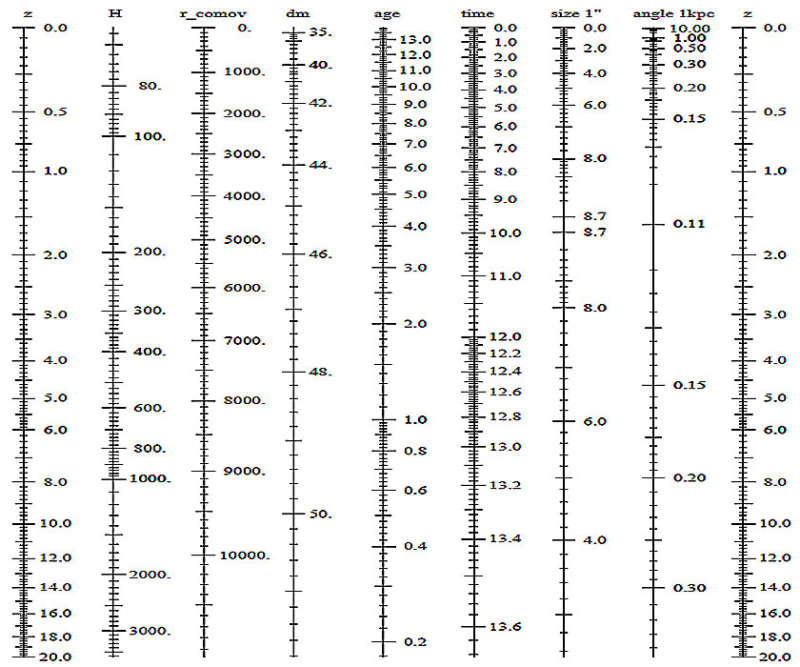
Все величины, помеченные индексом 0, относятся к моменту приёма волны t>t{\displaystyle \textstyle t_{0}>t}. Так как в расширяющейся Вселенной a(t)>a(t){\displaystyle \textstyle a(t_{0})>a(t)}, то z>{\displaystyle \textstyle z>0} и длина волны принимаемого сигнала больше, чем излучённого. Величина z=(λ−λ)λ{\displaystyle \textstyle z=(\lambda _{0}-\lambda )/\lambda }, называемая параметром красного смещения, равна относительному увеличению длины волны принимаемого электромагнитного сигнала.

В процессе расширения Вселенной изменяется не только длина (частота) электромагнитных волн, испущенных удалёнными от наблюдателя источниками. Так как Δt=(1+z)Δt{\displaystyle \textstyle \Delta t_{0}=(1+z)\Delta t}, то процессы (не обязательно периодические), протекающие в удалённых объектах, выглядят замедленными. В частности на фактор (1+z){\displaystyle \textstyle (1+z)} необходимо подправлять кривые светимости сверхновых Ia, являющихся «стандартными свечами» при проведении космологических наблюдений. Более удалённые сверхновые после взрыва гаснут медленнее, чем более близкие.

Динамика изменения функции a(t){\displaystyle \textstyle a(t)} в рамках ОТО обычно такова, что в некоторый фиксированный момент в прошлом (для которого выбирается начало отсчёта времени t={\displaystyle \textstyle t=0}) масштабный фактор равен нулю a()={\displaystyle \textstyle a(0)=0}. Свет, испущенный в этот момент, имеет красное смещение z=∞{\displaystyle \textstyle z=\infty }. На самом деле ранняя Вселенная была очень плотной и непрозрачной для излучения. Наблюдаемое в настоящее время реликтовое излучение испущено в момент времени, соответствующий эпохе рекомбинации с z∼1000{\displaystyle \textstyle z\sim 1000}. Наиболее удалённые, обнаруженные в настоящее время, сверхновые типа Ia обладают красными смещениями z<2{\displaystyle \textstyle z<2}. Для удалёных квазаров эта величина может достигать z∼6{\displaystyle \textstyle z\sim 6}.

Эвристический вывод гравитационного красного смещения из метрических свойств пространства-времени

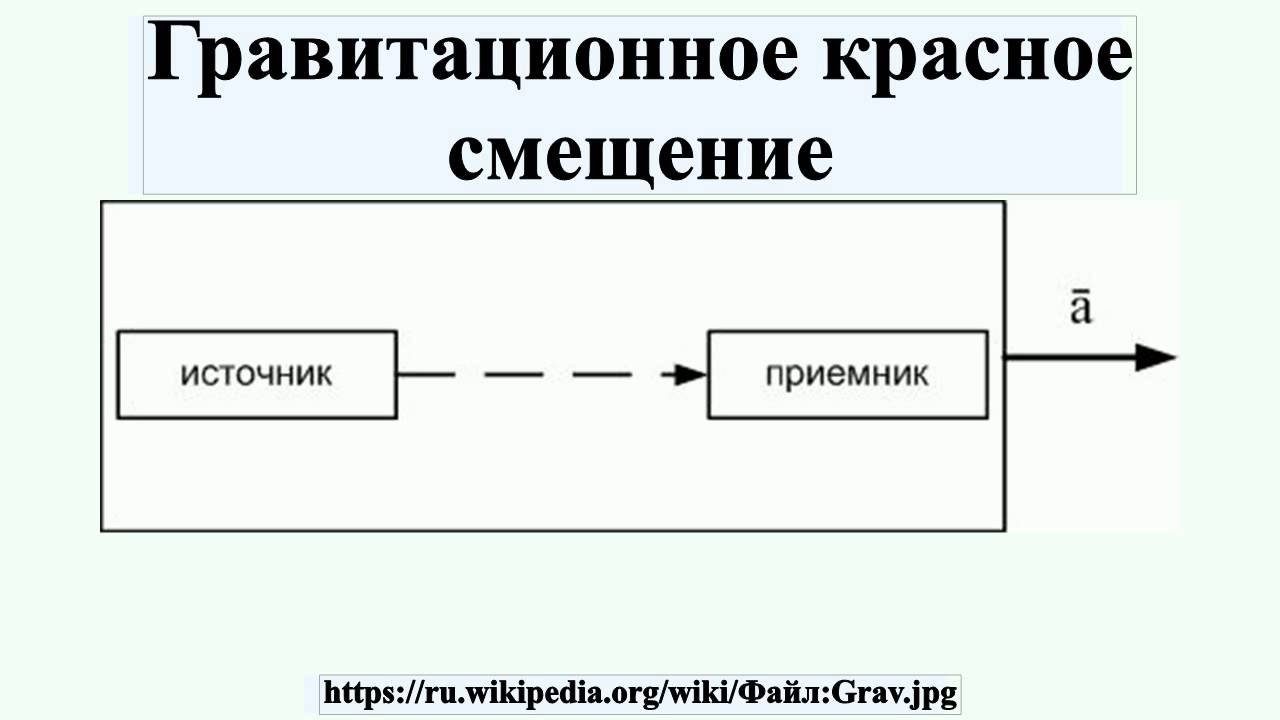
Ускоренная лаборатория, состоящая из источника пуль и приёмника

Гравитационное красное смещение можно получить, используя закон сложения скоростей.

Рассмотрим установку, состоящую из источника сигнала (к примеру, пуль) и приёмника. Расстояние между ними, измеренное в неподвижной системе отсчёта, обозначим l{\displaystyle l}. При этом установка двигается в пустоте с постоянным ускорением a→{\displaystyle {\vec {a}}} относительно неподвижной системы отсчёта, что, согласно принципу эквивалентности, равнозначно помещению установки в однородное гравитационное поле.

Далее, поместим в приёмник и источник одинаковые часы τout=τin{\displaystyle \tau _{out}=\tau _{in}}, и попросим наблюдателя, который находится в точке «приёмника», сравнить их ход. Своё собственное время τin{\displaystyle \tau _{in}} он измерит непосредственно, а чтобы измерить ход времени в точке «источника», он будет измерять частоту приходящего сигнала. Скорость пули относительно «источника» обозначим как w{\displaystyle w}, скорость самого источника в момент посылки сигнала v.{\displaystyle v.} Тогда, пользуясь законом сложения скоростей, получаем скорость пули u{\displaystyle u} в неподвижной системе:

u=w+v1+wvc2=c2(w+v)c2+wv.(1){\displaystyle u={\frac {w+v}{1+wv/c^{2}}}={\frac {c^{2}(w+v)}{c^{2}+wv}}.\qquad (1)}

На преодоление расстояния l{\displaystyle l} сигнал затратит время t,{\displaystyle t,} а приемник за это время сместится на vt+at22.{\displaystyle vt+at^{2}/2.} Отсюда получаем уравнение:

ut=l+vt+at22,{\displaystyle ut=l+vt+at^{2}/2,}

решив которое относительно t,{\displaystyle t,} получим:

t=u−va⋅1±(1−2al(u−v)2)−12{\displaystyle t={\frac {u-v}{a}}\cdot \left[1\pm \left(1-{\frac {2al}{(u-v)^{2}}}\right)^{-1/2}\right]}

или приближённо:

t=u−va⋅1±(1+la(u−v)2+⋯).{\displaystyle t={\frac {u-v}{a}}\cdot \left.}

Таким образом, приходим к двум решениям:

t1=−lu−v,t2=2u−va+lu−v.{\displaystyle t_{1}=-{\frac {l}{u-v}},\qquad t_{2}=2{\frac {u-v}{a}}+{\frac {l}{u-v}}.}

Очевидно, что первое решение в данном случае — лишнее.

Подставим u{\displaystyle u} из формулы (1) в формулу для t{\displaystyle t} и при этом ограничимся w{\displaystyle w} и v{\displaystyle v} столь малыми, чтобы мы могли отбросить малые члены порядка w2{\displaystyle w^{2}} и v2{\displaystyle v^{2}:}

t=l(c2+wv)wc2=l(1w+vc2).{\displaystyle t={\frac {l(c^{2}+wv)}{wc^{2}}}=l\left({\frac {1}{w}}+{\frac {v}{c^{2}}}\right).}

Скорость установки за время τ{\displaystyle \tau }, разделяющее посылку двух последовательных сигналов, увеличится на aτ{\displaystyle a\tau } и станет равной v+aτ{\displaystyle v+a\tau }. Поэтому разница во времени прохождения двух последовательных сигналов составит:

Δt=Δτ=l(1w+v+aτc2)−l(1w+vc2)=alτc2,{\displaystyle \Delta t=\Delta \tau =l\left({\frac {1}{w}}+{\frac {v+a\tau _{0}}{c^{2}}}\right)-l\left({\frac {1}{w}}+{\frac {v}{c^{2}}}\right)={\frac {al\tau _{0}}{c^{2}}},}

и в итоге

Δττ=alc2⟺τ1=τ(1+alc2).{\displaystyle {\frac {\Delta \tau }{\tau _{0}}}={\frac {al}{c^{2}}}\Longleftrightarrow \tau _{1}=\tau _{0}\left(1+{\frac {al}{c^{2}}}\right).}

Изменениями l{\displaystyle l} и τ{\displaystyle \tau } (функции скорости) мы пренебрегли, как величинами соответствующего порядка малости.

Итак, часы идут медленнее, если они установлены вблизи весомых масс. Отсюда следует, что спектральные линии света, попадающего к нам с поверхности больших звёзд, должны сместиться к красному концу спектра», писал .

Для частоты получим:

Δνν=alc2⟺ν1=ν(1−alc2).{\displaystyle {\frac {\Delta \nu }{\nu _{0}}}={\frac {al}{c^{2}}}\Longleftrightarrow \nu _{1}=\nu _{0}\left(1-{\frac {al}{c^{2}}}\right).}

Обозначив разность гравитационных потенциалов на поверхности звезды и поверхности Земли как ΔΦ=−al,{\displaystyle \Delta \Phi =-al,} получим:

τ1=τ(1−ΔΦc2);ν1=ν(1+ΔΦc2).{\displaystyle \tau _{1}=\tau _{0}\left(1-{\frac {\Delta \Phi }{c^{2}}}\right);\qquad \nu _{1}=\nu _{0}\left(1+{\frac {\Delta \Phi }{c^{2}}}\right).}

Эти выражения были выведены Эйнштейном в 1907 году для случая ΔΦc2≪1{\displaystyle \Delta \Phi /c^{2}\ll 1}.

Заключение

Польза и вред криля, свойства продукта определяются химическим составом мяса. Также важен способ приготовления и качество сырья. Перед введением в рацион мяса криля рекомендуется ознакомиться с противопоказаниями, проконсультироваться с врачом.

Была ли Вам данная статья полезной?

Да
Нет