Координатная прямая. точки на координатной прямой. как построить координатную прямую

Взаимно однозначное соответствие между точками координатной прямой и действительными числами

Нам известно, что на данной прямой линии лежит бесконечно много точек. Не является исключением и координатная прямая – она также содержит бесконечно много точек. Между точками координатной прямой и действительными числами существует очень важная связь, которую называют взаимно однозначным соответствием. Эта связь выражается следующим утверждением: каждой точке координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.

Озвученное утверждение, несомненно, нуждается в пояснении.

Отметим какую-нибудь точку на координатной прямой. Какое действительное число ей соответствует?

Если эта точка совпадает с началом отсчета (точкой O), то будем считать, что ей отвечает число нуль.

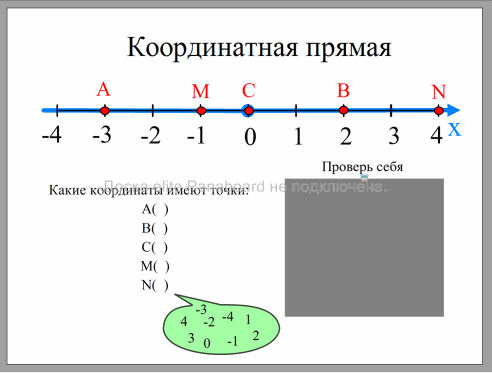
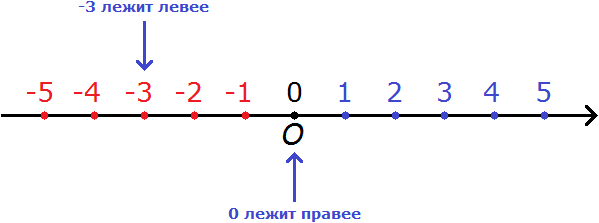
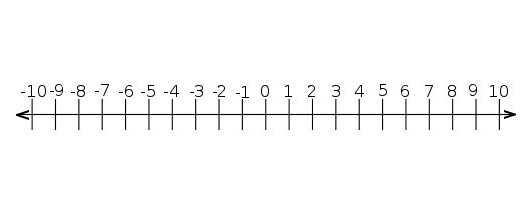
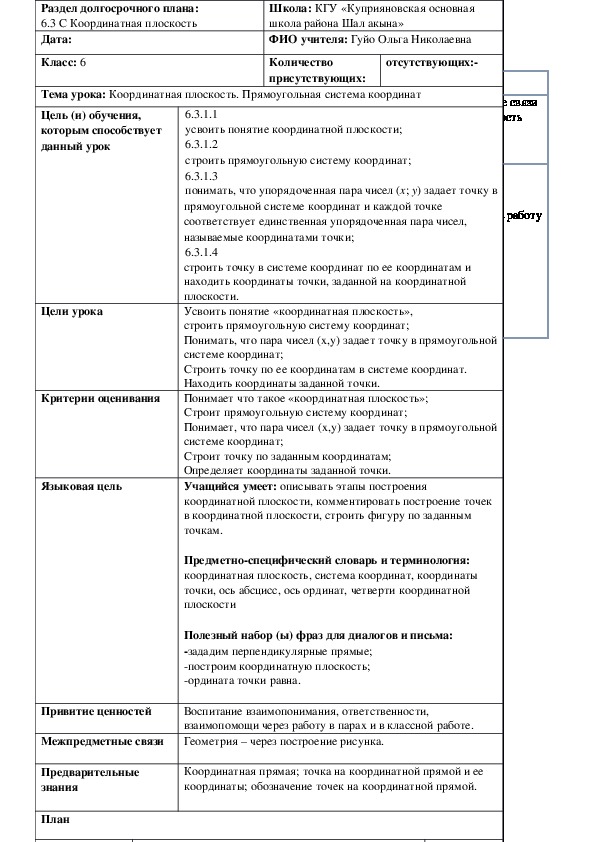
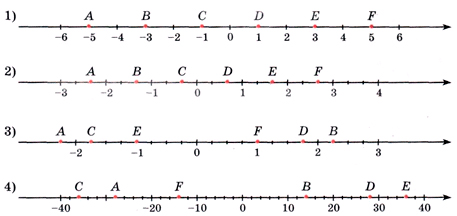
Если эта точка не совпадает с началом отсчета, то от точки O будем друг за другом последовательно откладывать единичные отрезки, пока не попадем в отмеченную точку. Если это произошло, то будем считать, что этой точке соответствует число, записанное над ней. Например, на рисунке ниже в точку М мы попадаем, отложив три единичных отрезка в отрицательном направлении, этой точке соответствует число -3.

Если же откладывание единичных отрезков на координатной прямой не приводит нас в отмеченную точку, то будем откладывать не только единичные отрезки, но и отрезки, составляющие одну десятую долю единичного отрезка, а при необходимости одну сотую долю, одну тысячную долю и так далее. На рисунке ниже в точку М мы попали, отложив в положительном направлении 1 единичный отрезок и 4 отрезка, составляющих десятую долю единичного отрезка. Этой точке соответствует рациональное число 1,4. А если на координатной прямой отложить в отрицательном направлении 17 единичных отрезков, 3 отрезка, составляющих сотую долю единичного, и 9 отрезков, составляющих стотысячную долю единичного, то мы попадем в точку, которой будет соответствовать число, противоположное числу 17,03009, то есть -17,03009 (при необходимости обращайтесь к материалу статьи противоположные числа).

Так единичный отрезок и его десятая, сотая и так далее доли позволяют нам попасть в точки координатной прямой, которым будут соответствовать конечные десятичные дроби (как в предыдущем примере). Однако на координатной прямой существуют точки, в которые мы не можем попасть, но к которым мы можем подойти сколь угодно близко, использую все меньшие и меньшие до бесконечно малой доли единичного отрезка. Этим точкам соответствуют бесконечные периодические и непериодические десятичные дроби. Приведем несколько примеров. Одной из таких точек на координатной прямой соответствует число 3,711711711…=3,(711). Чтобы подойти к этой точке нужно отложить 3 единичных отрезка, 7 его десятых долей, 1 сотую долю, 1 тысячную, 7 десятитысячных долей, 1 стотысячную, 1 миллионную долю единичного отрезка и так далее. А еще одной точке координатной прямой отвечает иррациональное число пи (π=3,141592…).

Так как элементами множества действительных чисел являются все числа, которые можно записать в виде конечных и бесконечных десятичных дробей, то вся вышеизложенная в этом пункте информация позволяет утверждать, что каждой точке координатной прямой мы поставили в соответствие конкретное действительное число, при этом понятно, что разным точкам соответствуют разные действительные числа.

Также достаточно очевидно, что это соответствие является взаимно однозначным. То есть, мы можем указанной точке на координатной прямой поставить в соответствие действительное число, но мы также можем по данному действительному числу указать конкретную точку на координатной прямой, которой отвечает данное действительное число. Для этого нам придется отложить от начала отсчета в нужном направлении определенное количество единичных отрезков, а также десятых, сотых и так далее долей единичного отрезка. Например, числу 703,405 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 703 единичных отрезка, 4 отрезка, составляющих десятую долю единичного, и 5 отрезков, составляющих тысячную долю единичного.

Итак, каждой точке на координатной прямой отвечает действительное число, и каждое действительное число имеет свое место в виде точки на координатной прямой. Вот почему координатную прямую очень часто называют числовой прямой.

Мимоходом заметим, что точкам, лежащим правее начала отсчета на числовой прямой, соответствуют положительные числа, а точкам, лежащим левее начала отсчета, — отрицательные. Подробнее об этом написано в статье положительные и отрицательные числа.

Применение

Координатная прямая – это основа простейших видов графиков, с которыми сталкивается школьник на своем учебном пути. Она используется практически в каждой математической теме: при расчёте скорости и времени, проецировании размеров объектов и вычислении их площади, в тригонометрии при работе с синусами и косинусами.

А про скорость речь идёт неспроста – именно её зачастую отображают графики функции. А ещё они могут отображать изменение температуры или давления внутри объекта, его размеров, ориентации относительно горизонта. Таким образом, построить координатную прямую зачастую требуется и в физике.

Плоскость

При построении двух прямых на координатной плоскости мы уже можем рассматривать графики функций. Скажем, горизонтальная линия будет осью времени, а вертикальная – расстоянием. И вот уже мы в состоянии определить, какое расстояние преодолеет объект через минуту или час пути. Таким образом, работа с плоскостью даёт возможность следить за изменением состояния объекта. Это гораздо интереснее, чем исследование статичного состояния.

Простейший график на такой плоскости – прямая, она отражает функцию Y(X) = aX + b. Линия изгибается? Это означает, что объект меняет свои характеристики в процессе исследования.

Отметки на горизонтальной координатной прямой по умолчанию получают название X1, X2,X3, а на вертикальной – Y1, Y2,Y3 соответственно. Проецируя их на плоскость и находя пересечения, мы находим фрагменты результирующего рисунка. Соединив их одной линией, мы получим график функции. В случае с падающим камнем квадратичная функция будет иметь вид: Y(X) = aX * X + bX + c.

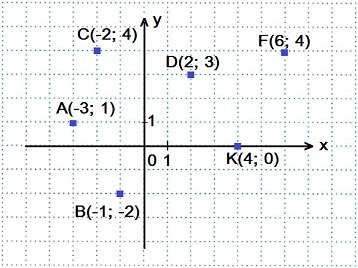
Определение координат

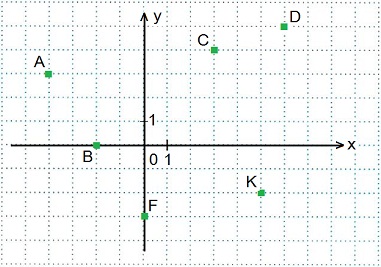
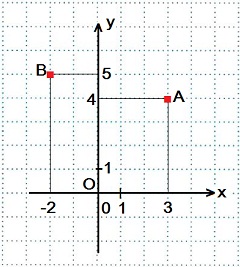
Для того чтобы определить координаты точки, опускают перпендикуляр на каждую из осей. Получаются два отрезка. Значение длин этих отрезков в заданных единицах длины и будет соответствовать координатам точки.

Соответственно, чтобы по координатам построить точку, нужно провести перпендикуляр из заданных точек на осях. В точке пересечения этих перпендикуляров и будет находиться искомая точка.

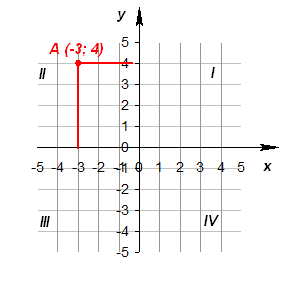
У координатной плоскости есть 4 четверти, в каждой из которых свои границы х и у. Будьте внимательны, координаты вполне могут быть отрицательными. Это всего лишь позволяет определить четверть координатной плоскости.

Что мы узнали?

Мы узнали, что такое координатная плоскость с координатами. Выделили элементы и квадраты координатной плоскости и поговорили о том, какие системы координат существуют. Рассказали о способе определения координат и построения точки по координатам. Выделили несколько нюансов построения координатной плоскости.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Размещаем фигуру

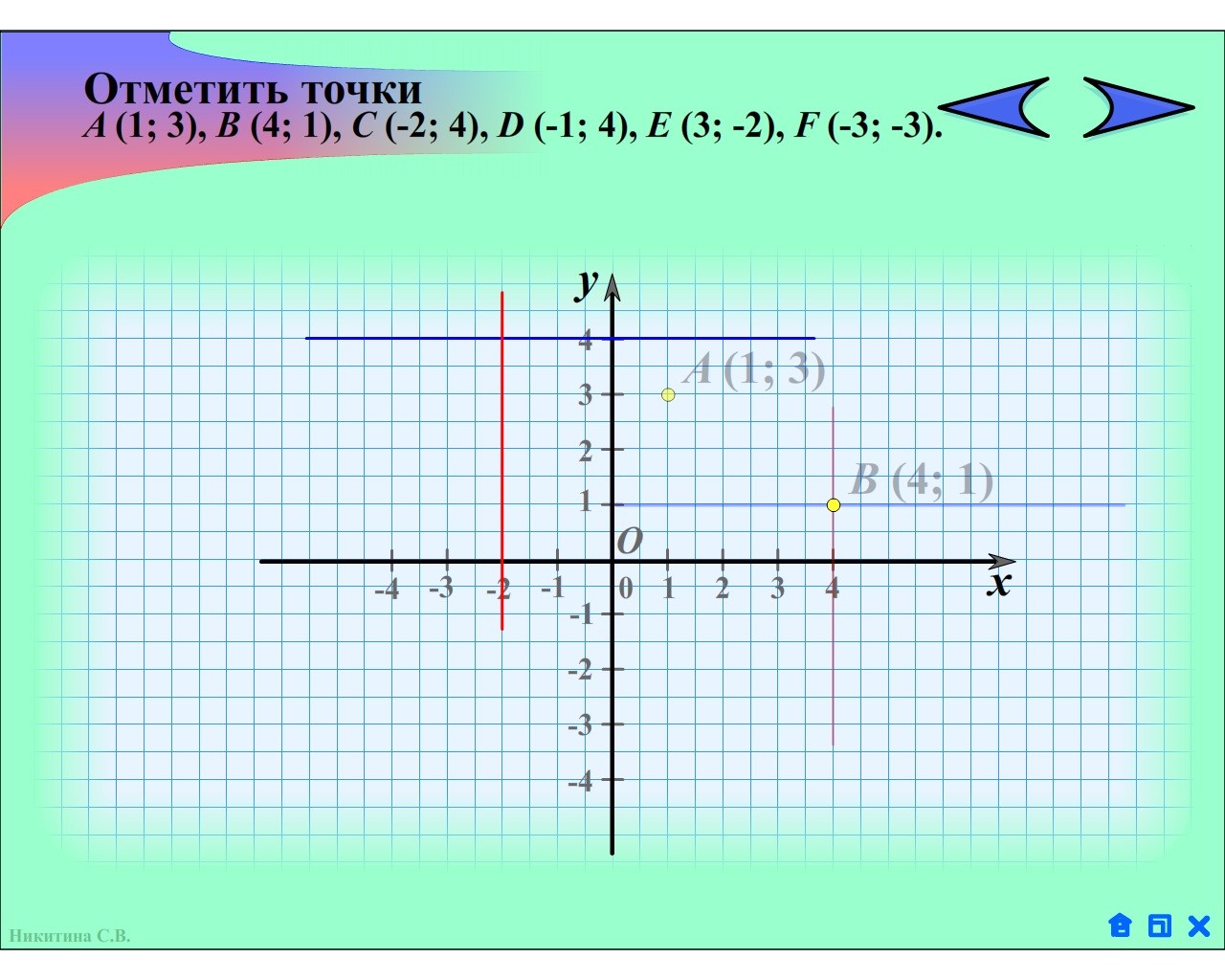
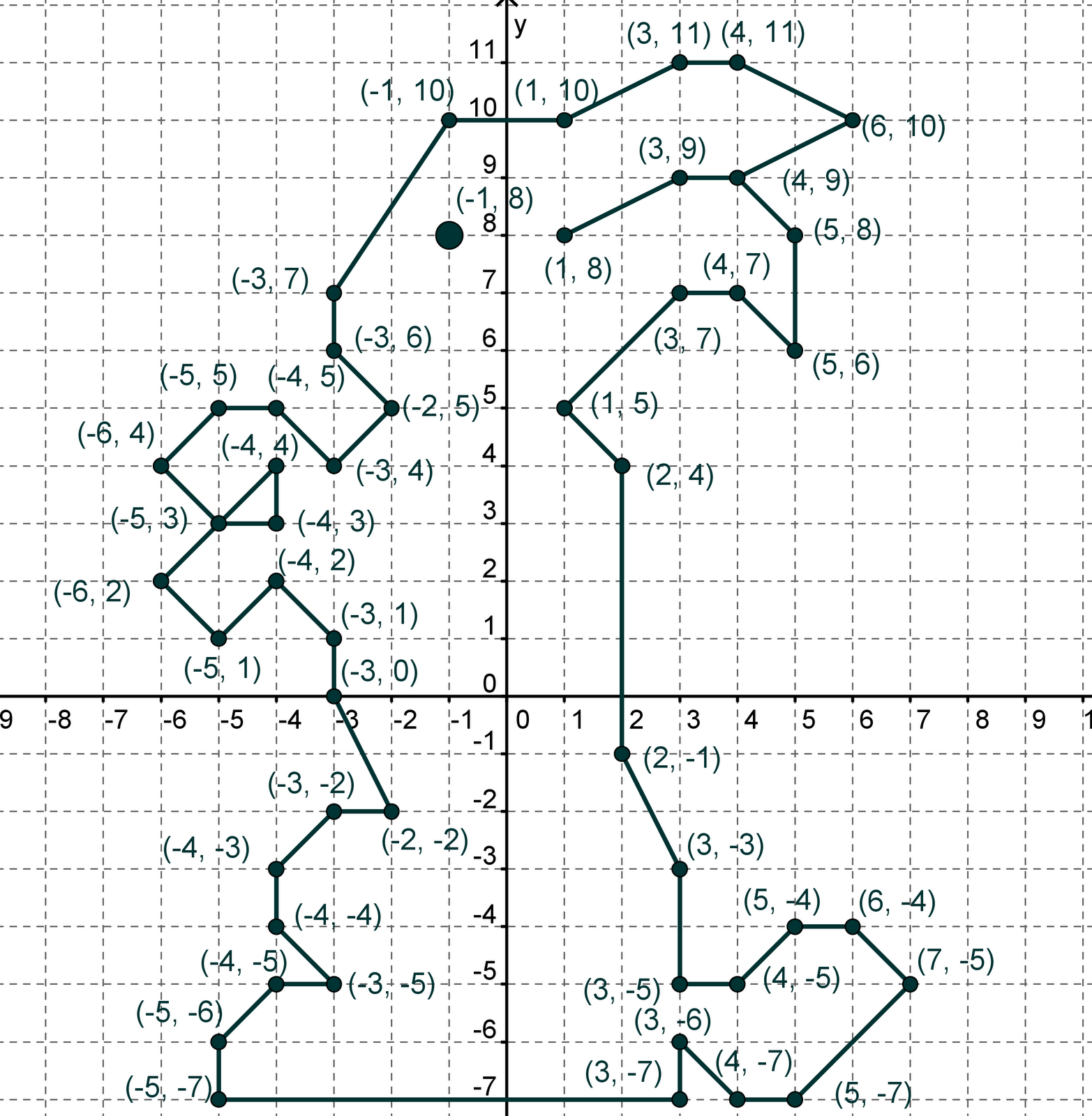
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.

В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.

Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.

Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.

Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.

Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.

Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.

Координатный луч

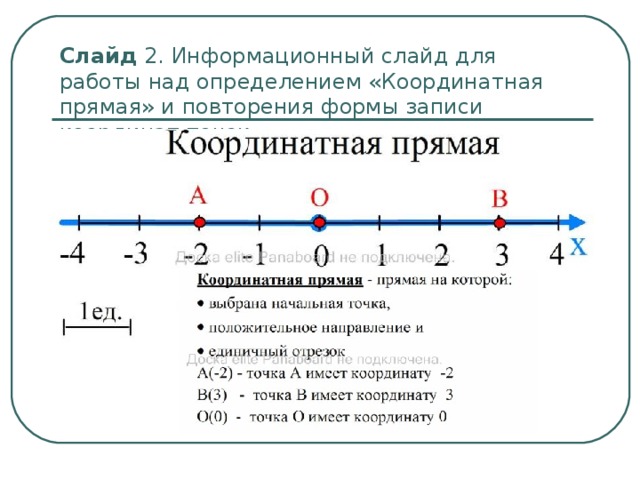
Чтобы определить координатный луч, нам сначала потребуется, конечно же, сам луч. Итак, построим луч, обозначим его OX, точка O – начало луча. Забегая вперед, скажем, что точку O называют началом отсчета координатного луча. Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала.

Так у нас есть луч. Как же его сделать координатным лучом?

Во-первых, над точкой O нужно написать число .

Во-вторых, нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1.

В-третьих, на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному, далее от конца этого отрезка нужно отложить еще один единичный отрезок, от конца построенного отрезка нужно отложить еще один единичный отрезок, и так далее.

Наконец, чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из : 2, 3, 4, …

Так координатный луч представляет собой не что иное, как бесконечную шкалу.

Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O, и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа и 1. Этот вариант изображения координатного луча приведен на рисунке ниже.

В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.

Также допускается буквы O и X записывать над лучом, а числа – под лучом.

Наконец, не удивляйтесь, если в обозначении координатного луча Вы увидите одновременно и маленькую и большую буквы. Наиболее часто придется сталкиваться с координатными лучами, обозначенными как Ox, Oy и Oz.

Отрицательные числа

Нередко требуется на практике работать с отрицательными значениями. В этом случае мы будем уходить по оси координат влево. Например, объект высотой 3 сантиметра плавает в воде. На треть он погружен в жидкость, на две трети находится на воздухе. Тогда, выбрав в качестве оси поверхность воды, мы с помощью простейших арифметических вычислений получаем два числа: верхняя точка объекта имеет координату (+2), а нижняя – (-1) сантиметр.

Нетрудно заметить, что в случае с плоскостью у нас образуется четыре четверти координатной прямой. Каждая из них имеет свой номер. В первой (верхней правой) части будут располагаться точки, имеющие две положительные координаты, во второй – слева сверху – значения по оси «икс» будут отрицательные, а по «игрек» — положительные. Третья и четвертая отсчитываются дальше против часовой стрелки.

Область применения

На самом деле, область применения координатного луча достаточно мала. Это могут быть:

• Рисунки к задачам
• Сравнение положительных или отрицательных чисел. Причем либо только положительных, либо только отрицательных
• Использование для отметки координат. Но декартова система куда удобнее. Хотя нельзя забывать, что декартова система представляет собой 4 координатных луча

На самом деле, это одна из гениальных идей математики: соединить вместе 4 координатных луча для получения системы ориентации на плоскости. Два луча лежат на одной прямой и направлены в противоположные стороны, при этом два других луча лежат на прямой, перпендикулярной первой и так же направлены в противоположные стороны.

В результате получилась система, которую уже несколько сотен лет применяют для ориентирования на плоскости. Более того, декартову систему можно перевести в пространство.

Эту систему навигации используют спутниковые системы, радары, навигационные системы автомобилей. Такой системой пользуются художники при использовании компьютерной графики. И всему этому положил начало координатный луч. Поэтому нельзя сказать, что он бесполезен. Просто луч имеет малую область применения, но именно он положил начал современным системам навигации.

Что мы узнали?

Мы поговорили об определении координатного луча. Выделили его отличия от числового луча и координатной прямой. Оговорили область применения и особенности координатного луча в математике 5 класса.

1. Вопрос 1 из 10

Начать тест(новая вкладка)

Координаты точки и отрезка

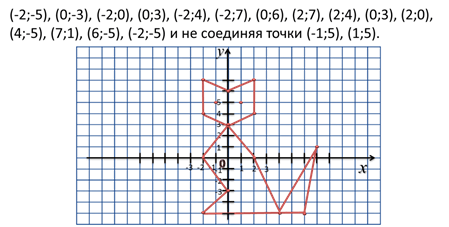
Когда на уроке дается математическая задача, в ней могут содержаться параметры различных геометрических фигур как в виде длин сторон, периметра, площади, так и в виде координат. В этом случае может потребоваться как построить фигуру, так и получить какие-то данные, связанные с ней. Возникает вопрос: как найти на координатной прямой требуемую информацию? И как построить фигуру?

Помните, как построить отрезок? Вы проходили это на геометрии. Если есть две точки, то между ними можно провести прямую. Их-то координаты и указываются в скобках, если в задаче фигурирует отрезок. Например: A(15, 13) – B(1, 4). Чтобы построить такую прямую, нужно на координатной плоскости найти и отметить точки, а затем их соединить. Вот и всё!

А любые многоугольники, как вы знаете, можно нарисовать с помощью отрезков. Задача решена.

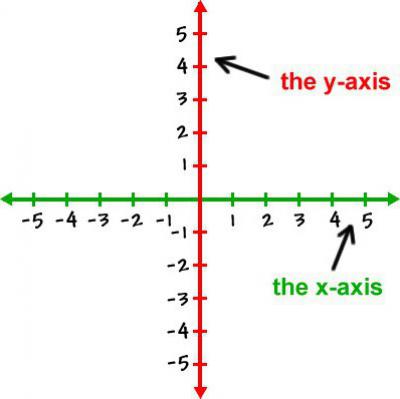
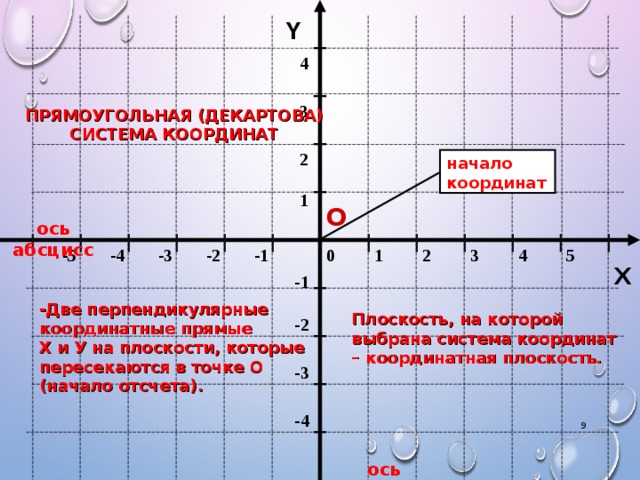
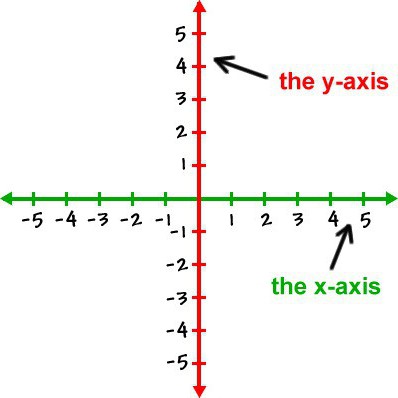
Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X′X{\displaystyle X’X} и Y′Y{\displaystyle Y’Y}. Оси координат пересекаются в точке O{\displaystyle O}, которая называется началом координат, на каждой оси выбрано положительное направление.

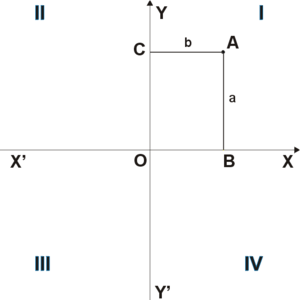
Рис. 1

Положение точки A{\displaystyle A} на плоскости определяется двумя координатами x{\displaystyle x} и y{\displaystyle y}. Координата x{\displaystyle x} равна длине отрезка OB{\displaystyle OB}, координата y{\displaystyle y} — длине отрезка OC{\displaystyle OC} в выбранных единицах измерения. Отрезки OB{\displaystyle OB} и OC{\displaystyle OC} определяются линиями, проведёнными из точки A{\displaystyle A} параллельно осям Y′Y{\displaystyle Y’Y} и X′X{\displaystyle X’X} соответственно.

При этом координате x{\displaystyle x} приписывается знак минус, если точка B{\displaystyle B} лежит на луче OX′{\displaystyle OX’} (а не на луче OX{\displaystyle OX}, как на рисунке). Координате y{\displaystyle y} приписывается знак минус, если точка C{\displaystyle C} лежит на луче OY′{\displaystyle OY’}. Таким образом,OX′{\displaystyle OX’} и OY′{\displaystyle OY’} являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Ось x{\displaystyle x} называется осью абсцисс, а ось y{\displaystyle y} — осью ординат. Координата x{\displaystyle x} называется абсциссой точки A{\displaystyle A}, координата y{\displaystyle y} — ординатой точки A{\displaystyle A}.

Символически это записывают так:

A(x,y){\displaystyle A(x,\;y)}

или

A=(x,y){\displaystyle A=(x,\;y)}

или указывают принадлежность координат конкретной точке с помощью индекса:

xA,xB{\displaystyle x_{A},x_{B}}

и т. д.

• В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y′Y{\displaystyle Y’Y} вверх, ось X′X{\displaystyle X’X} смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно — например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат).
• Четыре угла (I, II, III, IV), образованные осями координат X′X{\displaystyle X’X} и Y′Y{\displaystyle Y’Y}, называются координатными углами, четвертями или квадрантами <плоскости> (см. рис. 1).
  • Точки внутри координатного угла I имеют положительные абсциссы и ординаты.
  • Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.
  • Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты
  • Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.

Масштаб

Конечно, не обязательно выставлять рядом с делениями на прямой целочисленные значения. Если вы рассматриваете движение улитки, которая ползет со скоростью 0,03 метра в минуту, выставьте в качестве значений на координатной прямой дроби. В данном случае задайте цену деления как 0,01 метра.

Особенно удобно выполнять такие чертежи в тетради в клетку – здесь сразу видно, хватит ли места на листе для вашего графика, не выйдете ли вы за поля. Свои силы рассчитать несложно, ведь ширина клетки в такой тетради – 0,5 сантиметра. Понадобилось – уменьшили рисунок. От изменения масштаба графика он не потеряет и не изменит своих свойств.

Луч — альтернативные значения слова

Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.

Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.

Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:

• Солнце;
• звёзды;
• лампочка.

В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.

Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.

Кризис 2020 года: новости и прогнозы для России. Куда вложить и как сохранить деньги. Съем жилья или ипотека? Что выбрать? Считаем вместеКак хранить деньги почти без рискаКуда вложить деньги