Кинкинг внутренней сонной артерии: определение, особенности и лечение

Кинк в уравнении синус-Гордона

Рассмотрим теорию одного действительного скалярного поля в пространстве размерности 1+1{\displaystyle 1+1} с лагранжианом

Λ=ϕ,μϕ,μ+m2v2cos⁡ϕv−1.{\displaystyle \Lambda =\phi _{,\mu }\phi ^{,\mu }+m^{2}v^{2}.}

Принцип наименьшего действия приводит к уравнению

ϕ,μ μ+m2vsin⁡ϕv=,{\displaystyle \phi _{,\mu }^{~~\mu }+m^{2}v\sin {\frac {\phi }{v}}=0,}

Антикинк в уравнении синус-Гордона

которое заменой x→mx, t→mt, ϕ→ϕv{\displaystyle x\rightarrow mx,~~t\rightarrow mt,~~\phi \rightarrow {\frac {\phi }{v}}} приводится к уравнению синус-Гордона

ϕtt−ϕxx+sin⁡ϕ=,{\displaystyle \phi _{tt}-\phi _{xx}+\sin \phi =0,}

имеющему следующие частные решения, представляющие движущиеся со скоростью v{\displaystyle v} кинки, интерполирующие между вакуумами ϕ=2πk, k∈Z{\displaystyle \phi _{0}=2\pi k,~~k\in \mathbb {Z} } и ϕ+2π{\displaystyle \phi _{0}+2\pi } при изменении x{\displaystyle x} от −∞{\displaystyle -\infty } до +∞{\displaystyle +\infty }:

ϕ(x,t)=ϕ+4arctan⁡{exp⁡±x+vtv2−1+δ},{\displaystyle \phi (x,t)=\phi _{0}+4\arctan \left\{\exp \left\right\},}

где δ{\displaystyle \delta } — произвольная постоянная. Знак +{\displaystyle +} соответствует кинку, знак −{\displaystyle -} — антикинку.

Лечение заболевания

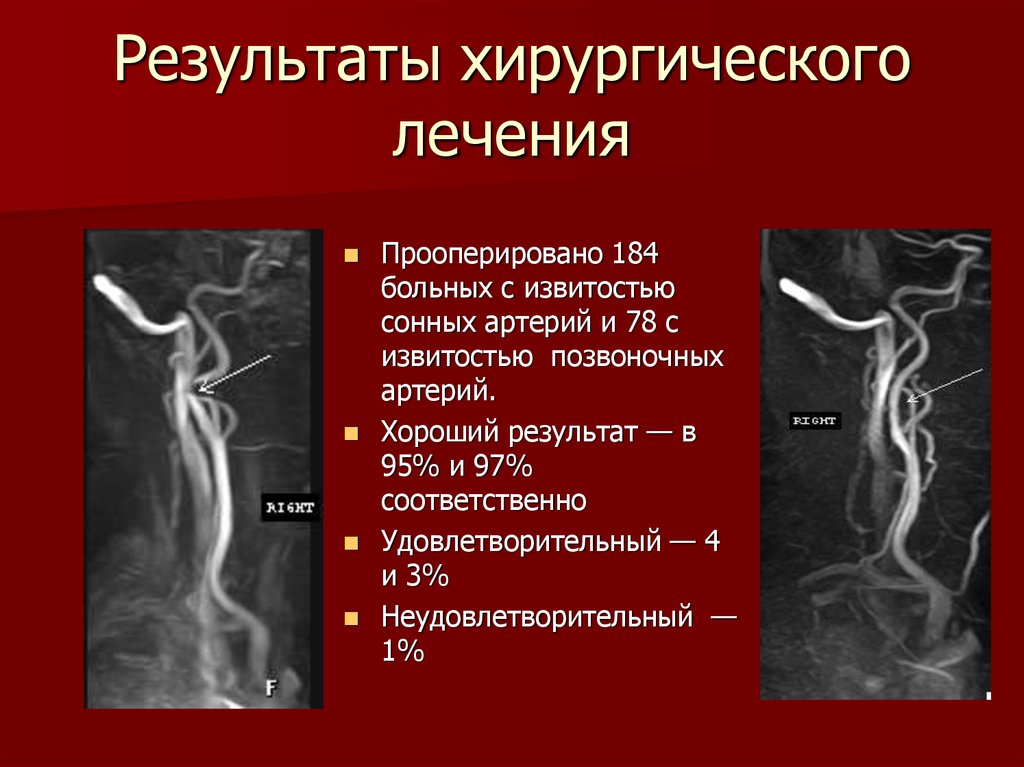
Единственной эффективной методикой терапии кинкинга считается оперативное вмешательство. В данном случае хирурги отсекают лишний участок артерии, распрямляя сосуд. В результате такой операции полностью восстанавливается кровоснабжение головы и мозга.

Поскольку такое оперативное вмешательство, благодаря современным медицинским методикам, является наименее травматичным, а его проведение редко занимает более 20 минут, то в большинстве случаев оно осуществляется под местной анестезией. После операции пациента направляют в стационар, а выписка его на амбулаторное лечение при отсутствии осложнений производится через один-два дня.

Эффективность операции очень высока. Все патологические симптомы полностью исчезают примерно у 95% пациентов. Вероятность возникновения осложнений составляет при этом не более 1%.

Медикаментозная терапия в данной ситуации малоэффективна, поскольку позволяет лишь облегчить симптоматику, однако не избавляет от самой проблемы – патологического изгиба сосуда.

Диагностика кинкинга

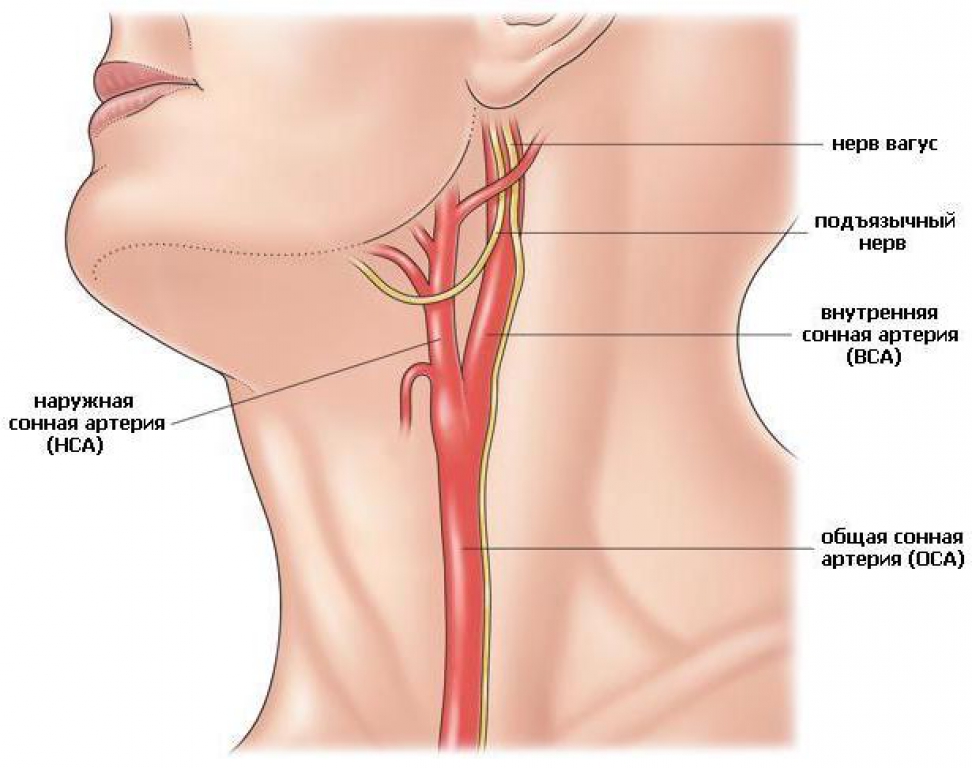
Для выявления кинкинга — патологической извитости внутренней сонной артерии, следует провести комплексные диагностические мероприятия. Для начала специалист проводит опрос больного, определяя ситуации и выявляя моменты, когда его самочувствие ухудшилось. В обязательном порядке осуществляется аускультация (прослушивание при помощи фонендоскопа) сонных артерий для определения наличия или отсутствия патологических шумов и измерение артериального давления.

Помимо этого, следует использовать одну из инструментальных диагностических методик:

УЗИ, которое помогает оценить структуру артериального сосуда и его стенок, а также узнать о качестве кровотока. Благодаря методу ультразвуковой допплерографии специалисты определяют риск закупорки сонных артерий.
Дуплексное сканирование, которое позволяет четко оценить структуру артерии, посредством ее визуализации.
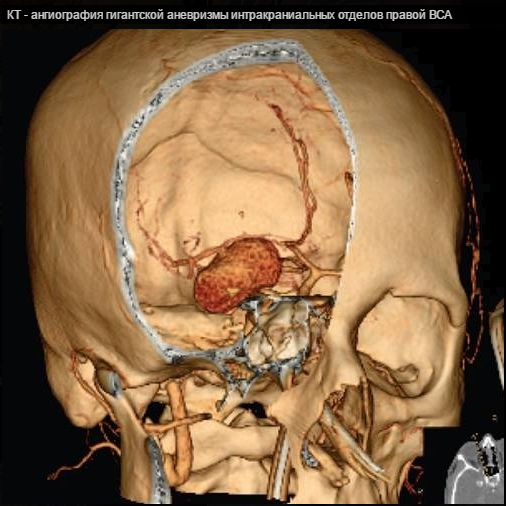
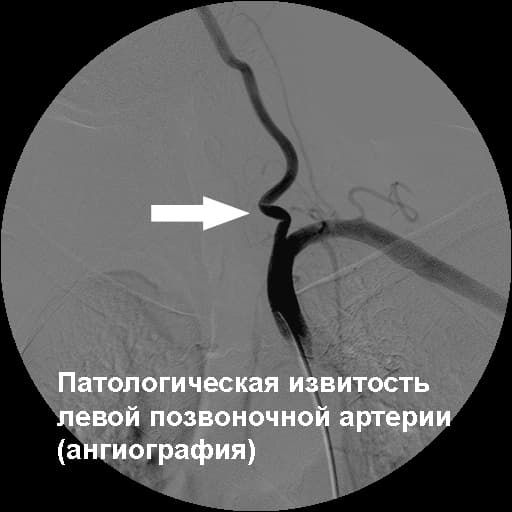
КТ- и МР-ангиографию, которые позволяют увидеть каждый из слоев сонной артерии и точную локализацию патологической деформации. Для улучшения качества картинки больному вводят в кровь специальное контрастирующее вещество.
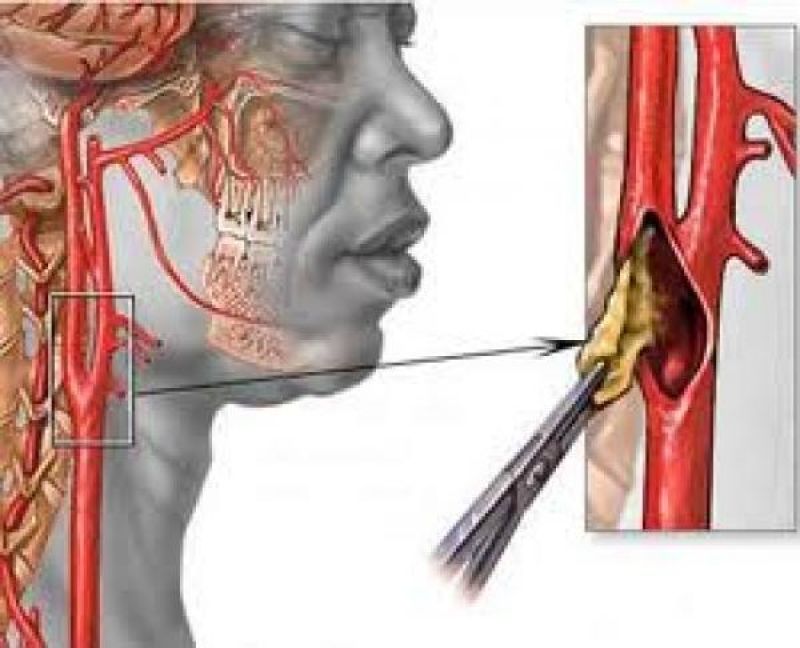
Селективную ангиографию. Данная методика предполагает применение рентгеновского излучения. При этом осуществляется прокол ВСА (внутренней сонной артерии), в просвет которой вводится контрастирующее вещество. Вследствие этого на мониторе специалист получает подробное изображение внутренних частей сосуда. Данная методика применяется только в крайних случаях, например, ее используют для установления целесообразности проведения оперативного вмешательства.

Причины развития кинкинга

В большинстве случаев кинкинг внутренней сонной артерии – это патология врожденного характера, однако зачастую развитию подобного заболевания способствуют иные факторы, в перечень которых входят:

возрастные сосудистые изменения;
постоянное высокое артериальное давление;
курение;
сахарный диабет;
нездоровое питание с большим количеством жиров и углеводов;
избыточный вес.

Огромную роль в развитии заболевания играет также наследственный фактор. Если у родственников было диагностирована данная патология, необходимо пройти диагностику. Провоцировать развитие кинкинга может стать малоподвижный образ жизни.

Кинк в модели одного действительного скалярного поля

Вид V(ϕ){\displaystyle V(\phi )} при λ=2, μ=2{\displaystyle \lambda =2,~~\mu ={\sqrt {2}}}.

Рассмотрим теорию одного действительного скалярного поля в пространстве размерности 1+1{\displaystyle 1+1} с действием

S=∫d2x12ϕ,μϕ,μ−V(ϕ),{\displaystyle S=\int d^{2}x\left,}

где ϕ{\displaystyle \phi } — потенциал поля, μ=,1{\displaystyle \mu =0,1}, а

V(ϕ)=−μ22ϕ2+λ4ϕ4+μ24λ=λ4(ϕ2−v2)2, v=μλ.{\displaystyle V(\phi )=-{\frac {\mu ^{2}}{2}}\phi ^{2}+{\frac {\lambda }{4}}\phi ^{4}+{\frac {\mu ^{2}}{4\lambda }}={\frac {\lambda }{4}}(\phi ^{2}-v^{2})^{2},~~v={\frac {\mu }{\sqrt {\lambda }}}.}

Действие инвариантно относительно дискретного преобразования ϕ=−ϕ{\displaystyle \phi =-\phi }; эта симметрия спонтанно нарушается, так как классические вакуумы равны ϕvac=±v{\displaystyle \phi ^{vac}=\pm v}.

Из принципа наименьшего действия получается уравнение поля

ϕ,μ μ+∂V(ϕ)∂ϕ={\displaystyle \phi _{,\mu }^{~~\mu }+{\frac {\partial V(\phi )}{\partial \phi }}=0.}

Гиперболический тангенс — статическое решение уравнений поля при x=, λ=2, μ=2{\displaystyle x_{0}=0,~~\lambda =2,~~\mu ={\sqrt {2}}}.

Будем искать статическое, то есть не зависящее от времени решение уравнений поля. В этом случае уравнение поля сводится к

ϕ″−∂V(ϕ)∂ϕ=,{\displaystyle \phi »-{\frac {\partial V(\phi )}{\partial \phi }}=0,}

где штрих обозначает производную по пространственной координате.
Полученное уравнение имеет следующее решение:

ϕ=vtanh⁡(±λ2v(x−x))=μλtanh⁡(±μ2x),{\displaystyle \phi =v\tanh(\pm {\sqrt {\frac {\lambda }{2}}}v(x-x_{0}))={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}x)},}

где x{\displaystyle x_{0}} — постоянная интегрирования. Данное решение и является простейшим статическим кинком, интерполирующим между вакуумами −v{\displaystyle -v} и +v{\displaystyle +v} при изменении пространственной координаты от −∞{\displaystyle -\infty } до +∞{\displaystyle +\infty }. Решение со знаком −{\displaystyle -} называется антикинком.

Свойства решения

Размер кинка имеет порядок величины rk=μ−1{\displaystyle r_{k}=\mu ^{-1}}, т.е. порядок комптоновской длины волны элементарного возбуждения. Действительно, плотность энергии кинка

ϵ(x)=12ϕ′2+V(ϕ)=λ2v41cosh4⁡(μ2(x−x)){\displaystyle \epsilon (x)={\frac {1}{2}}\phi ‘^{2}+V(\phi )={\frac {\lambda }{2}}v^{4}{\frac {1}{\cosh ^{4}({\frac {\mu }{\sqrt {2}}}(x-x_{0}))}}}

существенно отличается от нуля только в области |x−x|≲rk{\displaystyle |x-x_{0}|\lesssim r_{k}}.

Статическая энергия кинка равна

∫−∞∞ϵ(x)dx=23mv2,{\displaystyle \int _{-\infty }^{\infty }\epsilon (x)dx={\frac {2}{3}}mv^{2},}

где m=2μ{\displaystyle m={\sqrt {2}}\mu } — масса элементарного возбуждения.

Полученное решение не инвариантно относительно пространственных трансляций и преобразований Лоренца. Однако эти преобразования переводят решения уравнений поля в другие решения. Применяя трансляции и преобразование Лоренца, получим следующее семейство нестатических решений:

ϕ=μλtanh⁡(±μ2(x−x)−ut1−u2),{\displaystyle \phi ={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}{\frac {(x-x_{0})-ut}{\sqrt {1-u^{2}}}})},}

где u{\displaystyle u} — скорость движущегося кинка.

Кинк в модели одного комплексного скалярного поля

Рассмотрим теорию одного комплексного скалярного поля в пространстве размерности 1+1{\displaystyle 1+1} с лагранжианом

Λ=ϕ,μϕ¯,μ+μ2ϕϕ¯−λ2(ϕϕ¯)2.{\displaystyle \Lambda =\phi _{,\mu }{\bar {\phi }}^{,\mu }+\mu ^{2}\phi {\bar {\phi }}-{\frac {\lambda }{2}}(\phi {\bar {\phi }})^{2}.}

Принцип наименьшего действия приводит к следующим уравнениям поля:

ϕ,μ μ=μ2ϕ−λϕ2ϕ¯,{\displaystyle \phi _{,\mu }^{~~\mu }=\mu ^{2}\phi -\lambda \phi ^{2}{\bar {\phi }},}

ϕ¯,μ,μ=μ2ϕ¯−λϕ¯2ϕ.{\displaystyle {\bar {\phi }}_{,\mu }^{,\mu }=\mu ^{2}{\bar {\phi }}-\lambda {\bar {\phi }}^{2}\phi .}

Полученные уравнения имеют решением кинк из теории действительного скалярного поля

ϕ=ϕ¯=μλtanh⁡(±μ2x).{\displaystyle \phi ={\bar {\phi }}={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}x)}.}

Каким образом проводится лечение

Лечение гангрены и диабетической стопы необходимо проводить в условиях многопрофильного медицинского центра. Это возможно сделать без операции: один из основных этапов лечения – восстановление кровотока, выполняется путем малоинвазивного высокотехнологичного вмешательства на сосудах для лечения гангрены нижних конечностей без ампутации. Такие технологии доступны на сегодняшний день в различных клиниках, но наилучшие результаты достигаются только при выполнении таких вмешательств профессионалами с наибольшим опытом и при возможности выбора из различных технологий лечения. При этом важна не только операция, но и правильное медикаментозное лечение.

При этом для развития симптомов болезни характерно несколько стадий:

1 степень – поверхностные язвы на коже и небольшие раны;
2 степень – возникновение ран, распространяющихся глубже кожи, инфицирование ран;
3 степень – гангрена пальцев и части стопы;
4 степень – гангрена всей стопы.

Современный многопрофильный центр, в котором есть вся инфраструктура для лечения таких пациентов, может обеспечить лечение даже в тяжелых и запущенных случаях — в случае гангрены стопы, в том числе.

В зависимости от распространенности поражения (если процесс захватывает менее половины стопы), выделяют следующие виды гангрены нижних конечностей:

Сухая гангрена
Влажная гангрена;
Газовая гангрена (как разновидность влажной гангрены)

Лечение пациентов всегда многоэтапное. На первом этапе проводится медикаментозная коррекция пациента, после чего выполняется хирургическое вмешательство по удалению нежизнеспособных тканей (некрэктомия), пациент готовится ко второму этапу — операции по восстановлению кровотока – ангиопластике и стентированию артерий нижних конечностей. Третий этап — это лечение после операции: заживление ран и коррекция сопутствуюищх заболеваний

Особенностями поряжений артерий при сахарном диабете является то, что при этом часто сужаются артерии голени и стопы. Для операции на артериях стопы для лечения критической ишемии нижних конечностей с гарантией результата требуется специальный высокотехнологичное оборудование, инструментарий, специальные навыки и опыт. Такие операции возможно провести безболезненно для пациента.

Частозадаваемые вопросы

ЧТО МНЕ НЕОБХОДИМО ДЕЛАТЬ ПОСЛЕ ВЫПИСКИ И ПОСЛЕ ЗАЖИВЛЕНИЯ РАНЫ НА СТОПЕ?

Статьи

10.06.2016
Гангрена нижних конечностей — приговор к ампутации, или что-то можно сделать?
Гангрена — возникновение участка омертвевших тканей у живого организма (см. определение Википедии). Гангрена нижних конечностей — опасное состояние, которое заключается в омертвении тканей чаще стопы, реже- голени или бедра из-за недостаточного питания тканей, как результат нарушения магистрального кровотока в нижних конечностей при…
31.05.2016
Сухая гангрена нижних конечностей
Гангрена – сложное заболевание, которое заключается в омертвении живой ткани, как правило, на стопе, и нарушении опорной функций пострадавших конечностей
20.05.2019
Срок жизни тканей на стопе

Разновидности сосудистых патологий

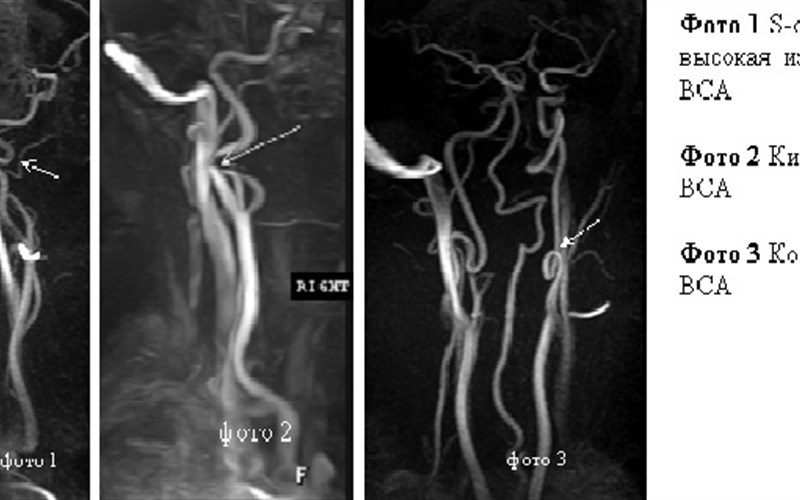
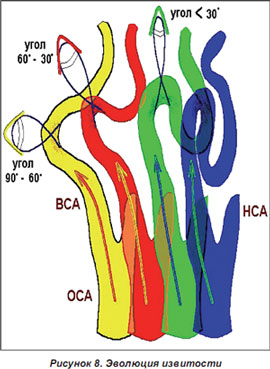
Одной из самых распространенной причин нарушений мозгового кровотока считается извитая структура сонной артерии. Более чем у 28% пациентов, скончавшихся от инсульта, была обнаружена данная патология. Почти у каждого четвертого при комплексном обследовании определяется удлинение или извитость этого сосуда.

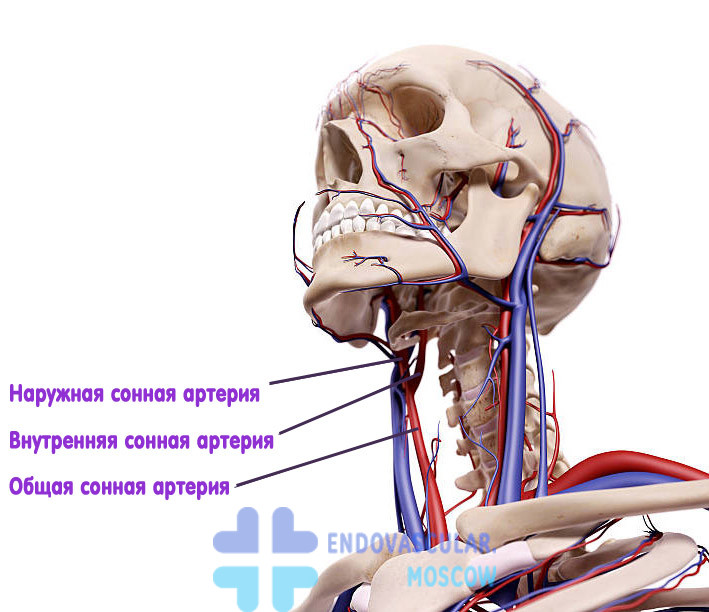
Специалисты выделяют следующие разновидности извитости внутренней сонной артерии:

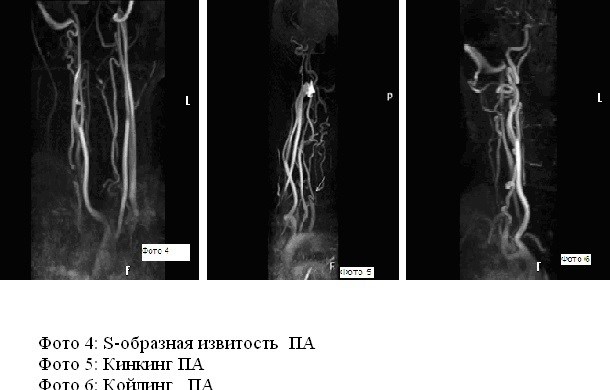
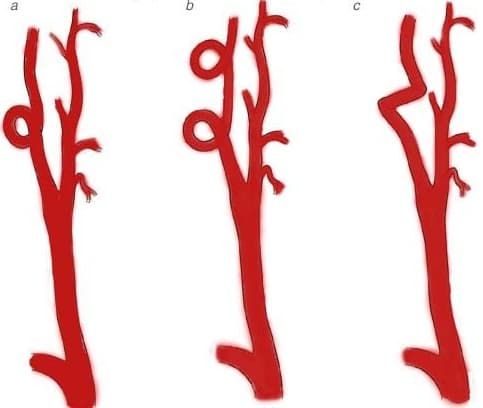
S-образная извитость. В данном случае артерия имеет несколько большие размеры, чем нужно, вследствие чего сосуд имеет S-образную форму. На начальных стадиях патологического процесса это не доставляет особого дискомфорта, однако с годами сосуд постепенно продолжает удлиняться, что значительно усугубляет подобное нарушение.
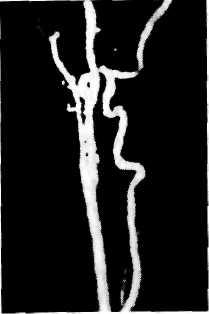
Кинкинг внутренней сонной артерии, который представляет собой патологический перегиб артериального сосуда под острым углом. Если патология является врожденной, заболевание весьма быстро выявляется. В остальных ситуациях пациент может продолжительное время лечить гипертонию, даже не догадываясь, что именно лежит в основе проблемы повышения артериального давления. Бывает кинкинг правой внутренней сонной артерии, а также левой. Нередко больного мучают и иные симптомы, например, мигрень, безосновательные панические вспышки и тошнота.
Койлинг, представляющий собой петлеобразную извитость сосуда. В данной ситуации скорость кровотока существенно затормаживается, приступы тошноты и головной боли, характерные для подобных случаев, появляются без влияния каких-либо внешних причин.

Кинк в модели одного действительного скалярного поля

Вид V(ϕ){\displaystyle V(\phi )} при λ=2, μ=2{\displaystyle \lambda =2,~~\mu ={\sqrt {2}}}.

S=∫d2x12ϕ,μϕ,μ−V(ϕ),{\displaystyle S=\int d^{2}x\left,}

где ϕ{\displaystyle \phi } — потенциал поля, μ=,1{\displaystyle \mu =0,1}, а

Из принципа наименьшего действия получается уравнение поля

ϕ,μ μ+∂V(ϕ)∂ϕ={\displaystyle \phi _{,\mu }^{~~\mu }+{\frac {\partial V(\phi )}{\partial \phi }}=0.}

Гиперболический тангенс — статическое решение уравнений поля при x=, λ=2, μ=2{\displaystyle x_{0}=0,~~\lambda =2,~~\mu ={\sqrt {2}}}.

ϕ″−∂V(ϕ)∂ϕ=,{\displaystyle \phi »-{\frac {\partial V(\phi )}{\partial \phi }}=0,}

ϕ=vtanh⁡(±λ2v(x−x))=μλtanh⁡(±μ2x),{\displaystyle \phi =v\tanh(\pm {\sqrt {\frac {\lambda }{2}}}v(x-x_{0}))={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}x)},}

Свойства решения

ϵ(x)=12ϕ′2+V(ϕ)=λ2v41cosh4⁡(μ2(x−x)){\displaystyle \epsilon (x)={\frac {1}{2}}\phi ‘^{2}+V(\phi )={\frac {\lambda }{2}}v^{4}{\frac {1}{\cosh ^{4}({\frac {\mu }{\sqrt {2}}}(x-x_{0}))}}}

существенно отличается от нуля только в области |x−x|≲rk{\displaystyle |x-x_{0}|\lesssim r_{k}}.

Статическая энергия кинка равна

∫−∞∞ϵ(x)dx=23mv2,{\displaystyle \int _{-\infty }^{\infty }\epsilon (x)dx={\frac {2}{3}}mv^{2},}

где m=2μ{\displaystyle m={\sqrt {2}}\mu } — масса элементарного возбуждения.

ϕ=μλtanh⁡(±μ2(x−x)−ut1−u2),{\displaystyle \phi ={\frac {\mu }{\sqrt {\lambda }}}\tanh {(\pm {\frac {\mu }{\sqrt {2}}}{\frac {(x-x_{0})-ut}{\sqrt {1-u^{2}}}})},}

где u{\displaystyle u} — скорость движущегося кинка.

Лечение в детском возрасте

Терапия кинкинга сонной артерии в детском возрасте имеет некоторые особенности. Вообще, выявлять это заболевание у детей стали относительно недавно, что связано с отсутствием в большинстве медучреждений необходимой диагностической аппаратуры.

Чаще всего весьма эффективной методикой лечения кинкинга у детей является оперативное вмешательство. Но, учитывая тот факт, что ребенок находится в постоянном развитии, иногда устранить вылечить такую патологию возможно без хирургических манипуляций. В некоторых случаях извитость проходит самостоятельно по мере роста ребенка. Такое явление наблюдается практически в 30% случаев. Улучшить кровоснабжение мозга и предупредить развитие ишемических нарушений можно при помощи специальных упражнений, которые показывает специалист. В случае, если подобные упражнения положительного эффекта не дают, врачи прибегают к оперативному вмешательству, особенно в ситуациях, когда ребенок чувствует себя очень плохо.

Симптомы патологического явления

Чаще всего люди с кинкингом внутренней сонной артерии жалуются на следующую симптоматику:

частое возникновение головной боли, которая не проходит после приема обезболивающих медикаментов;
периодически усиливающийся шумовые и звуковые явления в ушах;
периодические обмороки, которые могут длиться пару секунд;
туман или мелькание мурашек перед глазами;
нарушения координации движений;
в более сложных случаях – речевые нарушения и слабость верхних конечностей.

Таким образом, симптомы кинкинга левой внутренней сонной артерии либо правой очень схожи с рядом иных сосудистых заболеваний, например, распространенным среди пожилых людей атеросклерозом сосудов. Для определения заболевания необходимо провести целый ряд необходимых диагностических процедур.