История термина
Термин «энергия» происходит от греческого слова ἐνέργεια, которое впервые появилось в работах Аристотеля и обозначало действие или действительность (то есть действительное осуществление действия в противоположность его возможности). Это слово, в свою очередь, произошло от греческого ἔργον («эргон») — «работа». Праиндоевропейский корень werg обозначал работу или деятельность (ср. англ. work, нем. Werk) и в виде οργ/ουργ присутствует в таких греческих словах, как оргия или теургия и т. п.
Томас Юнг первым использовал понятие «энергия» в современном смысле слова
Прибор Джоуля для измерения механического эквивалента тепла. Нисходящий груз, прикрепленный к струне, вызывает вращение погруженного в воду весла.
Лейбниц в своих трактатах 1686 и 1695 годов ввёл понятие «живой силы» (vis viva), которую он определил как произведение массы объекта и квадрата его скорости (в современной терминологии — кинетическая энергия, только удвоенная). Кроме того, Лейбниц верил в сохранение общей «живой силы». Для объяснения уменьшения скорости тел из-за трения, он предположил, что утраченная часть «живой силы» переходит к атомам.
Маркиза Эмили дю Шатле в книге «Учебник физики» (фр. Institutions de Physique, 1740), объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда.
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия «живая сила». Гаспар-Гюстав Кориолис раскрыл связь между работой и кинетической энергией в 1829 году. Уильям Томсон (будущий лорд Кельвин) впервые использовал термин «кинетическая энергия» не позже 1851 года, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».
Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.
Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Инженеры (Сади Карно), физики (Джеймс Джоуль, Эмиль Клапейрон и Герман Гельмгольц), математики — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии». Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия». В 1881 году Уильям Томсон заявил перед слушателями:
В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла» (англ. dynamical theory of heat) и «энергетика» (англ. energetics). В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.
Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика (англ. thermoeconomics). Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.
В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется потому, что законы физики не изменяются с течением времени (см. Теорема Нётер, изотропия пространства).
В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии:
Что такое энергия?
В теории, выдвинутой Альбертом Эйнштейном, изучается взаимосвязь материи и энергии. Этот великий ученый смог доказать способность одной субстанции превращаться в другую. При этом выяснилось, что энергия является самым важным фактором существования тел, а материя вторична.
Энергия – это, по большому счету, способность выполнять какую-то работу. Именно она стоит за понятием силы, способной двигать тело или придавать ему новые свойства. Что же означает термин «энергия»? Физика – это фундаментальная наука, которой посвятили свою жизнь многие ученые разных эпох и стран. Еще Аристотель использовал слово «энергия» для обозначения деятельности человека. В переводе с греческого языка «энергия» — это «деятельность», «сила», «действие», «мощь». Первый раз это слово появилось в трактате ученого-грека под названием «Физика».
В общепринятом сейчас смысле данный термин был введен в обиход английским ученым-физиком Томасом Юнгом. Это знаменательное событие произошло в далеком 1807 году. В 50-х годах XIX в. английский механик Уильям Томсон впервые использовал понятие «кинетическая энгергия», а в 1853 г. шотландский физик Уильям Ренкин ввел термин «потенциальная энергия».
Сегодня эта скалярная величина присутствует во всех разделах физики. Она является единой мерой различных форм движения и взаимодействия материи. Другими словами, она представляет собой меру преобразования одних форм в другие.

Задачи на кинетическую энергию и решение
Задача 1 на нахождение кинетической энергии
Слон в 6000 кг бежит со скоростью 10 м / с. Какова его кинетическая энергия? Какова скорость пушечного ядра весом 1 кг, если у него была та же самая кинетическая энергия слона?
Ответ
Используя уравнение кинетической энергии, энергия слона равна:
Рассчитав кинетическую энергию, мы можем получить скорость пули, очистив v:
Это означает, что скорость пули равна 775 м / с. Сравните это со скоростью слона: вот это разница!
Задача 2
Мужчина врезался в столб на своей машине. Когда он пошел, чтобы сообщить о катастрофе, он сказал, что ехал с допустимой скоростью во время аварии. Но следователь помнил физику 7 и 8 класса и установил, что скорость транспортного средства была в два раза выше, чем утверждал водитель. Какова взаимосвязь между кинетической энергией и скоростью, сообщаемой человеком, и кинетической энергией со скоростью, рассчитанной следователем?
Ответ
Мы будем рассматривать Ec1 как кинетическую энергию транспортного средства на скорости v1, сообщаемой человеком, и Ec2 как кинетическую энергию со значением скорости v2, рассчитанным исследователем. Соотношение между кинетическими энергиями рассчитывается путем деления энергий следующим образом:
Следователь сказал, что скорость во время аварии была вдвое выше, чем сообщал человек, то есть:
Подставим значение скорости в уравнение:
Исключая похожие термины, мы имеем:
Это означает, что кинетическая энергия в соответствии со скоростью, сообщаемой человеком, составляет четверть кинетической энергии по расчетам следователя. Проще говоря, ущерб, нанесенный автомобилем, был в четыре раза больше, чем сообщал мужчина.
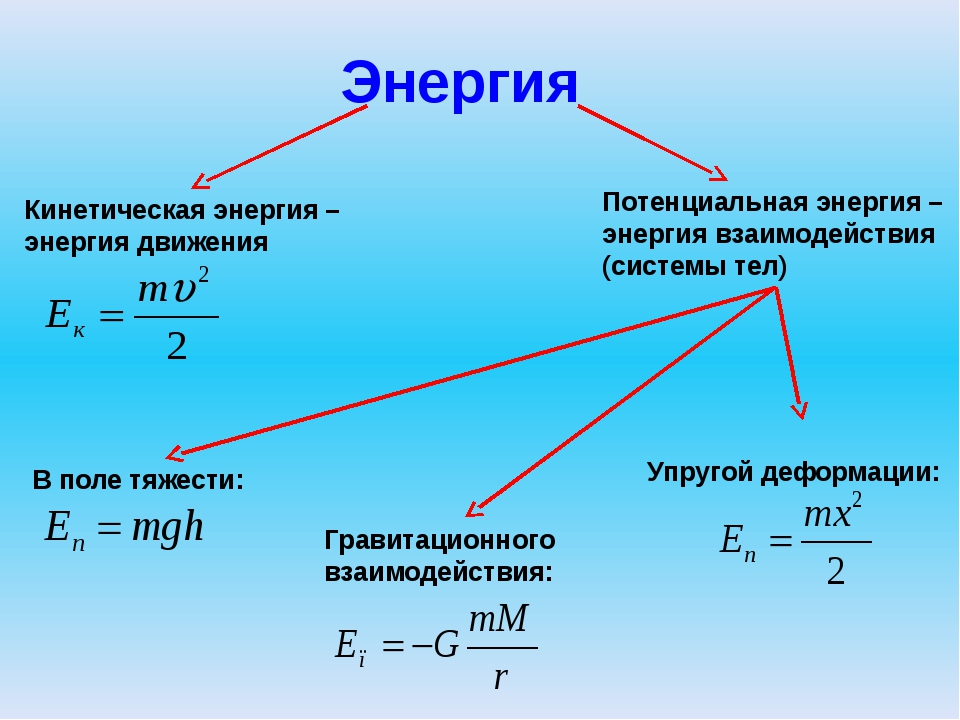
Потенциальная
Этим видом энергии обладают тела, которые находятся в каком-либо силовом поле. Так, магнитная возникает, когда объект находится под действием магнитного поля. Все тела, находящиеся на земле, обладают потенциальной гравитационной энергией.
В зависимости от свойств объектов изучения они могут иметь различные виды потенциальной энергии. Так, упругие и эластичные тела, которые способны вытягиваться, имеют потенциальную энергию упругости либо натяжения. Любое падающее тело, которое было ранее неподвижно, теряет потенциальную и приобретает кинетическую. При этом величина этих двух видов будет равнозначна. В поле тяготения нашей планеты формула энергии потенциальной будет иметь следующий вид:
Еп = mhg,где m — масса тела; h – высота центра массы тела над нулевым уровнем; g – ускорение свободного падения.
В словах эту формулу можно выразить так: потенциальная энергия объекта, взаимодействующего с Землей, равна произведению его массы, ускорению свободного падения и высоты, на которой оно находится.
Эта скалярная величина является характеристикой запаса энергии материальной точки (тела), находящейся в потенциальном силовом поле и идущей на приобретение кинетической энергии за счет работы сил поля. Иногда ее называют функцией координат, являющейся слагаемым в лангранжиане системы (функция Лагранжа динамической системы). Эта система описывает их взаимодействие.
Потенциальную энергию приравнивают к нулю для некой конфигурации тел, расположенных в пространстве. Выбор конфигурации определяется удобством дальнейших вычислений и называется «нормировкой потенциальной энергии».

Тенденции
В 2006 году около 18 % мирового потребления энергии было удовлетворено из возобновляемых источников энергии, причём 13 % из традиционной биомассы, таких, как сжигание древесины. В 2010 году 16,7 % мирового потребления энергии поступало из возобновляемых источников. В 2015 году этот показатель составил 19,3 %. Доля традиционной биомассы постепенно сокращается, в то время как доля современной возобновляемой энергии растёт.
С 2004 по 2013 годы доля электроэнергии, производимой в Евросоюзе из возобновляемых источников, выросла с 14 % до 25 %. В 2018 году в Германии из возобновляемых источников было произведено 38 % электроэнергии.
По прогнозу ИЭИ РАН и Центра энергетики Московской школы управления «Сколково», к 2040 г. ВИЭ обеспечат 35-50% мирового производства электроэнергии и 19-25% всего энергопотребления.
Гидроэлектроэнергия является крупнейшим источником возобновляемой энергии, обеспечивая 3,3 % мирового потребления энергии и 15,3 % мировой генерации электроэнергии в 2010 году. Использование энергии ветра растет примерно на 30 процентов в год, по всему миру с установленной мощностью 318 гигаватт (ГВт) в 2013 году, и широко используется в странах Европы, США и Китае. Производство фотоэлектрических панелей быстро нарастает, в 2008 году было произведено панелей общей мощностью 6,9 ГВт (6900 МВт), что почти в шесть раз больше уровня 2004 года. Солнечные электростанции популярны в Германии и Испании. Солнечные тепловые станции действуют в США и Испании, а крупнейшей из них является станция в пустыне Мохаве мощностью 354 МВт. Крупнейшей в мире геотермальной установкой является установка на гейзерах в Калифорнии с номинальной мощностью 750 МВт.
Бразилия проводит одну из крупнейших программ использования возобновляемых источников энергии в мире, связанную с производством топливного этанола из сахарного тростника. Этиловый спирт в настоящее время покрывает 18 % потребности страны в автомобильном топливе. Топливный этанол также широко распространен в США.
Крупные несырьевые компании поддерживают использование возобновляемой энергии. Так, IKEA собирается к 2020 году полностью обеспечивать себя за счёт возобновляемой энергии. Apple — крупнейший владелец солнечных электростанций, и за счёт возобновляемых источников энергии работают все дата-центры компании. Доля возобновляемых источников в энергии, потребляемой , составляет 35 %. Инвестиции компании в возобновляемую энергетику превысили $2 млрд.
| Глобальные показатели возобновляемой энергии | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ежегодные инвестиции в возобновляемую энергию (109 доллар США) | 130 | 160 | 211 | 257 | 244 | 232 | 270 | 286 | 241 | 280 |
| Суммарные установленные мощности возобновляемой электроэнергии (ГВт) | 1,140 | 1,230 | 1,320 | 1,360 | 1,470 | 1,578 | 1,712 | 1,849 | 2,017 | 2,195 |
| Гидроэлектроэнергия (ГВт) | 885 | 915 | 945 | 970 | 990 | 1,018 | 1,055 | 1,064 | 1,096 | 1,114 |
| Ветроэнергетика (ГВт) | 121 | 159 | 198 | 238 | 283 | 319 | 370 | 433 | 487 | 539 |
| фотоэлектричество (ГВт) | 16 | 23 | 40 | 70 | 100 | 138 | 177 | 227 | 303 | 402 |
| Нагрев воды тепловой энергией Солнца | 130 | 160 | 185 | 232 | 255 | 373 | 406 | 435 | 456 | 472 |
| Производство этанола (109 литры) | 67 | 76 | 86 | 86 | 83 | 87 | 94 | 98 | 99 | 106 |
| Производство биодизеля (109 литры) | 12 | 17.8 | 18.5 | 21.4 | 22.5 | 26 | 29.7 | 30.3 | 30.8 | 31 |
| Количество стран, имеющих цели развития возобновляемой энергии | 79 | 89 | 98 | 118 | 138 | 144 | 164 | 173 | 176 | 179 |
Кинетическая энергия в классической механике
Случай одной материальной точки
По определению, кинетической энергией материальной точки массой m{\displaystyle m} называется величина
- T=mv22{\displaystyle T={{mv^{2}} \over 2}},
при этом предполагается, что скорость точки v{\displaystyle v} всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}) данное выражение примет вид T=p22m{\displaystyle \ T=p^{2}/2m}.
Если F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}. Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} и учитывая, что a→=dv→dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}, причём d(v2)dt=d(v→⋅v→)dt=2v→⋅dv→dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}, получим F→ds→=d(mv22)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}.
Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина T{\displaystyle \ T} остаётся постоянной, то есть кинетическая энергия является интегралом движения.
Случай абсолютно твёрдого тела
При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:
- T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}
Здесь M{\displaystyle \ M} — масса тела, v{\displaystyle \ v} — скорость центра масс, ω→{\displaystyle {\vec {\omega }}} и I{\displaystyle I} — угловая скорость тела и его момент инерции относительно , проходящей через центр масс.
В специальной теории относительности
Энергия и масса
Основная статья: Эквивалентность массы и энергии
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна:
- E=mc2,{\displaystyle E=mc^{2},}
- где E{\displaystyle E} — энергия системы;
- m{\displaystyle m} — её масса;
- c{\displaystyle c} — скорость света в вакууме.
Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.
Энергия тела, согласно законам классической механики, зависит от системы отсчёта, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью v{\displaystyle v} относительно некоего наблюдателя, то для другого наблюдателя, движущегося с той же скоростью, оно будет казаться неподвижным. Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, mv22{\displaystyle mv^{2}/2}, где m{\displaystyle m} — масса тела, а для другого наблюдателя — нулю.
Эта зависимость энергии от системы отсчёта сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчёта к другой используется сложная математическая конструкция — тензор энергии-импульса.
Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:
- E=mc21−v2c2,{\displaystyle E={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}},}
- где m{\displaystyle m} — инвариантная масса. В системе отсчёта, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:
- E=mc2.{\displaystyle E_{0}=mc^{2}.}
Это минимальная энергия, которую может иметь тело, обладающее массой. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна указывает абсолютное значение этой постоянной.
Энергия и импульс
Специальная теория относительности рассматривает энергию как компоненту 4-импульса (4-вектора энергии-импульса), в который наравне с энергией входят три пространственные компоненты импульса. Таким образом энергия и импульс оказываются связанными и оказывают взаимное влияние друг на друга при переходе из одной системы отсчёта в другую.
Типы потенциальной энергии
Существуют различные типы потенциальной энергии, каждый из которых связан с определенным типом силы.
Четыре основных типа:
- Гравитационная Потенциальная Энергия: энергия в объекте, когда она удерживается вертикально на некоторой высоте.
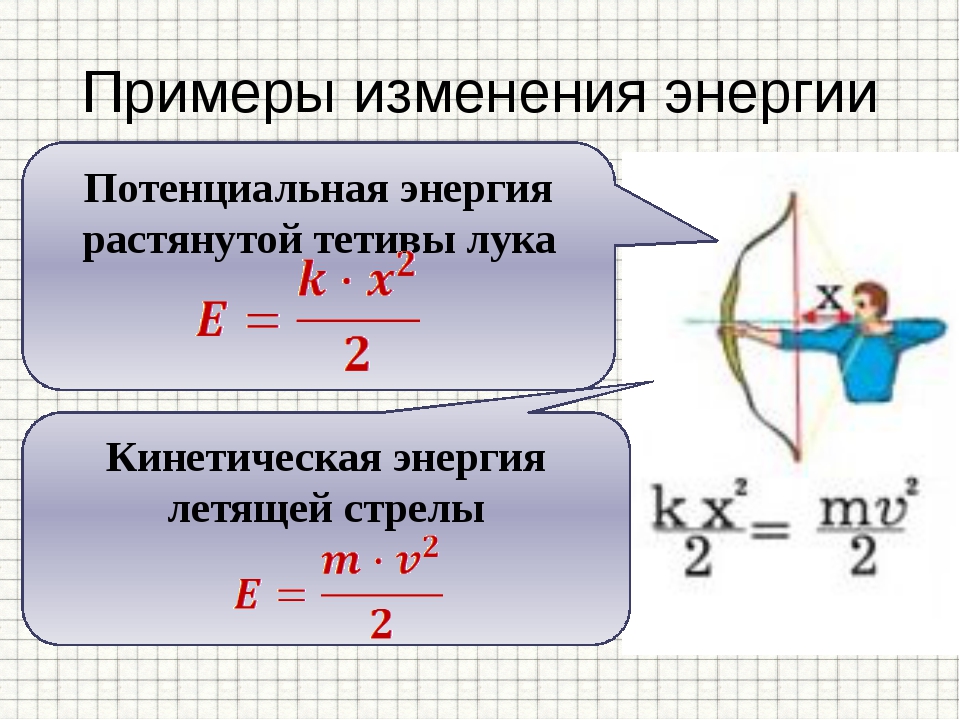
- Упругая потенциальная энергия: энергия, запасенная в объекте, когда он растягивается или сжимается.
- Потенциальная электрическая энергия: энергия в объекте за счет его заряда.
- Химическая потенциальная энергия: энергия, запасенная в химических связях вещества.
Каждый из них измеряется по-разному. Например, потенциальная энергия гравитации (PE) пропорциональна массе (m) объекта, силе тяжести (g) и высоте (h), на которой удерживается объект.
PE = m. g. h
Чем больше масса объекта и чем выше он удерживается, тем больше будет его потенциальная энергия. Как и все другие формы энергии, потенциальная энергия измеряется в килограммах-метрах в квадрате за секунду в квадрате (кг м2 / С2 ) или Джоуле (Дж).
Чтобы лучше объяснить этот феномен, мы собрали несколько интересных примеров потенциальной энергии, которую вы видите в своей повседневной жизни.
Возобновляемые и невозобновляемые источники энергии
Такие ресурсы, как солнце и ветер, являются возобновляемыми источниками энергии.
Закон сохранения энергии гласит, что энергия не может быть создана или уничтожена, может только быть преобразована. Это означает, что при подсчете количества энергии в системе это количество всегда будет одинаковым, хотя и по-разному.
Когда мы говорим о возобновляемых или невозобновляемых энергоресурсах, мы действительно имеем в виду источники или ресурсы, из которых люди извлекают энергию.
Уголь и нефть являются ископаемым топливом, в котором химическая энергия сохраняется в связях между атомами углерода. Ископаемое топливо не возобновимо, потому что оно было сформировано миллионы лет назад из доисторических организмов. Эти источники энергии, помимо ограниченного существования, наносят серьезный ущерб окружающей среде.
Наша цель должна заключаться в том, чтобы воспользоваться другими источниками энергии, такими как солнце, ветер, внутреннее земное тепло и океанские волны, которые являются возобновляемыми и не загрязняющими окружающую среду. Вода может использоваться снова и снова благодаря естественному процессу круговорота воды.
Другой аспект, который мы должны принять во внимание, это не тратить энергию. Электрическая энергия вашего дома имеет свою стоимость. Если у вас долгое время открыт холодильник (кстати, почему он открывается с трудом во второй раз) или вы оставили лампы в своей комнате, особенно если вас там нет, вы увеличиваете потребление электроэнергии в своем доме, и это будет оплачиваться вашими родителями. Экономия энергии – это разумное и осознанное использование
Атомные электростанции
Тип: Ядерная потенциальная энергия
Ядерная потенциальная энергия-это потенциальная энергия субатомных частиц (таких как протоны и нейтроны), присутствующих внутри ядра атома. Она удерживает протоны и нейтроны вместе, образуя ядро.
Когда два или более атомных ядра объединяются, чтобы сформировать большое ядро (ядерный синтез), высвобождается огромное количество энергии. Точно так же, когда одно ядро распадается на два меньших ядра (деление ядер), оно высвобождает большое количество энергии.
Атомные электростанции используют такие ядерные реакции (в основном ядерное деление урана и плутония) для получения тепла, которое затем используется в паровых турбинах для производства электроэнергии.
По сравнению с другими источниками энергии атомные электростанции используют меньшее количество сырья, имеют нулевой выброс, являются более мощными и эффективными.
Электрическая мощность
Электрические батареи превращают химическую энергию в электрическую.
Электричество – это тип энергии, который зависит от притяжения или отталкивания электрических зарядов. Существует два вида электричества: статическое и текущее. Статическое электричество связано с наличием статических нагрузок, т.е. нагрузок, которые не двигаются. Электрический ток происходит из-за перемещение грузов.
Пример статического электричества – когда мы натираем воздушный шарик на волосы. Воздушный шар удерживает электроны от волос, заряжаясь отрицательно, в то время как волосы заряжены положительно. Если вы подойдете к воздушному шарику к своей голове, не касаясь его, вы увидите, как пряди волос тянутся к воздушному шарику.
Электрический ток – это поток зарядов из-за движения свободных электронов в проводнике. Это движение происходит в электрическом поле, то есть в области вокруг заряда, где действует сила. Электрические заряды легко переносятся такими материалами, как металлы, особенно серебро, медь и алюминий.
В батареях или электрических батареях происходит превращение химической энергии в электрическую энергию. Химическая энергия происходит в результате реакции между электродами и электролитом, когда положительный полюс соединен с отрицательным полюсом батареи. Вольт – это единица измерения потенциальной энергии на заряд в батарее.
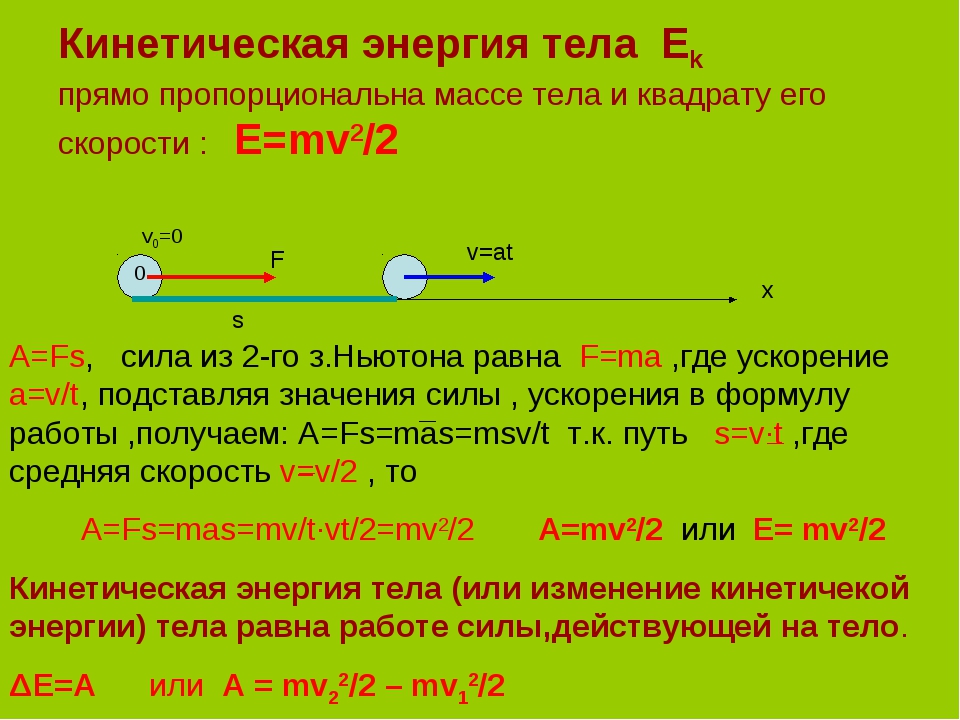
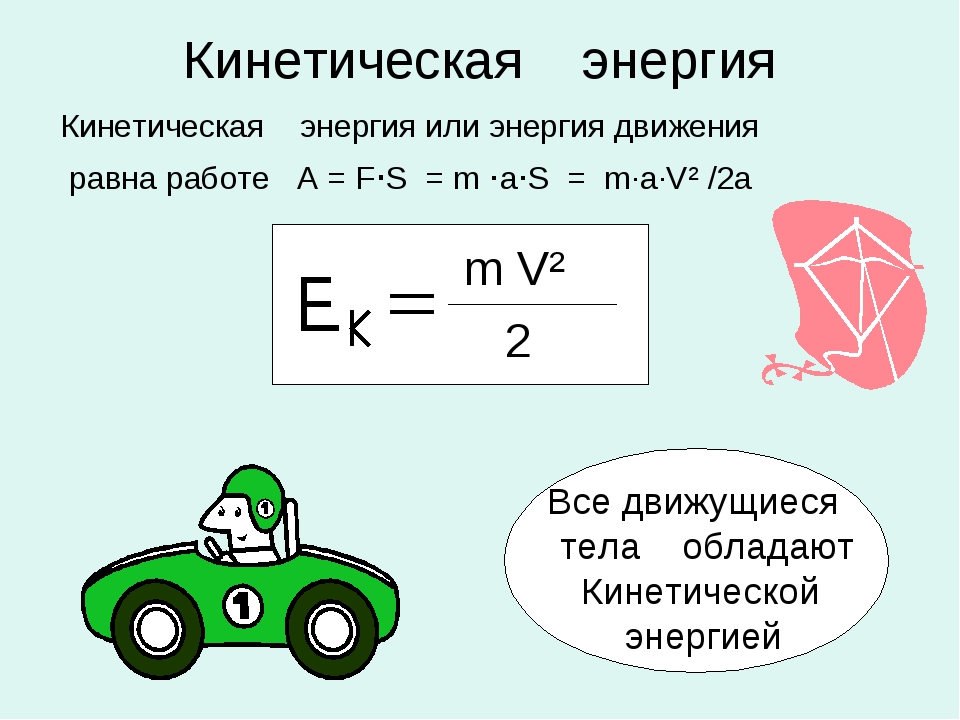
Кинетическая энергия, или энергия движения
Мы выяснили, что тело обладает энергией покоя, которая зависит от его месторасположения. Но что произойдет, если тело придет в движение? Что будет с энергией упавшего листа или камня?
О падающих листьях можно сказать, что тела движутся. В ходе падения сокращается расстояние до поверхности Земли, следовательно, уменьшается и потенциальная энергия. Согласно одному из признаков энергии, она не исчезает, а лишь преобразуется из одного вида в другой. Потенциальная энергия листьев преобразуется в энергию движения. Энергия движения, или кинетическая энергия, представляет собой способность тела выполнять работу благодаря движению. Когда лист достигает поверхности Земли, наибольшая часть его потенциальной энергии уже преобразовалась в кинетическую.
При падении большой камень может раздавить автомобиль своей кинетической энергией.
Величина кинетической энергии зависит от скорости и массы тела.
Кинетическая энергия выражается формулой:
Здесь Ек – кинетическая энергия, m – масса тела, v – скорость движущегося тела.
Под воздействием силы тяжести при падении листа выполняется работа, равная по величине его изначальной потенциальной энергии. При соприкосновении листа с поверхностью Земли имеющаяся у него кинетическая энергия преобразуется в тепловую.
Энергия – это способность тела выполнять работу.прикладывать силу.находиться на одном месте. Энергия, которая есть у тела благодаря его месторасположению, называется потенциальнойкинетической энергией. Энергию движения также называют потенциальнойкинетической энергией. ПотенциальнаяКинетическая энергия зависит от силы тяжести и скоростивысотымассы. Например, потенциальнаякинетическая энергия висящего на дереве яблока большеменьше, чем у лежащего на земле. ПотенциальнаяКинетическая энергия зависит от высотымассы и скорости тела. Если скорость тела увеличится в два раза, то его потенциальнаякинетическая энергия увеличится в двачетыредесять раз(а).
Механическая энергия
Этот вид энергии изучается в разделе физики, называемом «Механикой». Она обозначается буквой Е. Ее измерение осуществляется в джоулях (Дж). Что собой представляет эта энергия? Физика механики изучает движение тел и взаимодействие их друг с другом либо с внешними полями. При этом энергия, обусловленная движением тел, называется кинетической (обозначается Ек), а энергию, обусловленную взаимодействием тел или внешних полей, именуют потенциальной (Еп). Сумма движения и взаимодействия представляет собой полную механическую энергию системы.
Для расчета обоих видов существует общее правило. Для определения величины энергии следует вычислить работу, необходимую для перевода тела из нулевого состояния в данное состояние. При этом чем больше работа, тем большей энергией будет обладать тело в данном состоянии.
Кинетическая энергия в релятивистской механике
Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как
- T=mc21−v2c2−mc2,{\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}
где m{\displaystyle \ m} — масса, v{\displaystyle \ v} — скорость движения в выбранной инерциальной системе отсчёта, c{\displaystyle \ c} — скорость света в вакууме (mc2{\displaystyle mc^{2}} — энергия покоя). Как и в классическом случае, имеет место соотношение F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}, получаемое посредством умножения на ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} выражения второго закона Ньютона (в виде F→=m⋅d(v→1−v2c2)dt{\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}).
Выражение для T{\displaystyle \ T} можно переписать в форме T=mv2(1−v2c2+1−v2c2).{\displaystyle T=mv^{2}/(1-v^{2}/c^{2}+{\sqrt {1-v^{2}/c^{2}}}).} При малых скоростях (v≪c{\displaystyle v\ll c}) оно переходит в классическую формулу T=12⋅mv2{\displaystyle \ T=1/2\cdot mv^{2}}.
Примечания
- ↑ , с. 49.
- Тарг С. М. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
- Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
- ↑ Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
- , с. 54.
- Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
Кинетическая энергия в гидродинамике
В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dMdV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}}, то есть плотность кинетической энергии wT=dTdV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V} (Дж/м3), запишется:
- wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}
где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.
Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса. Если, в согласии с методом Рейнольдса, представить ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:
- wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}
где Es=ρ¯vα¯vα¯2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯2+ρ′vα′vα′¯2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности», часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.
Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.