История открытия
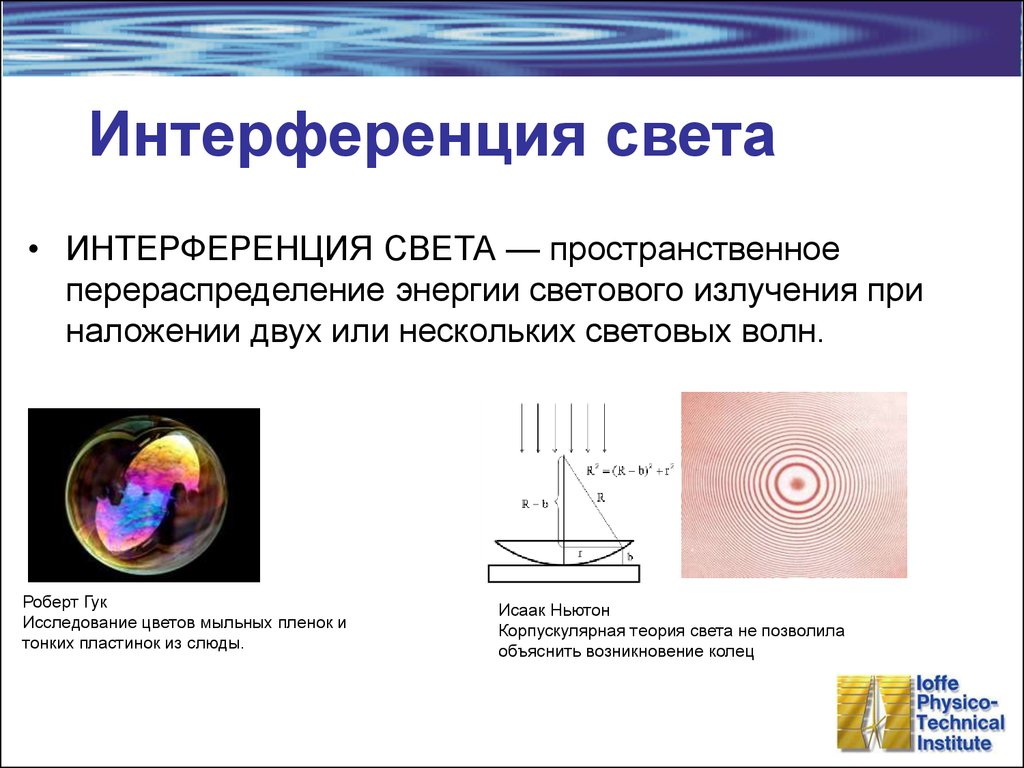
Впервые явление интерференции было независимо обнаружено Гримальди (для луча, прошедшего через два близких отверстия), Робертом Бойлем и Робертом Гуком (для интерференции в тонких слоях прозрачных сред, таких как мыльные плёнки, тонкие стенки стеклянных шаров, тонкие листки слюды; они наблюдали при этом возникновение разноцветной окраски; при этом Гук заметил и периодическую зависимость цвета от толщины слоя). Гримальди впервые и связал явление интерференции с идеей волновых свойств света, хотя ещё в довольно туманном и неразвитом виде.
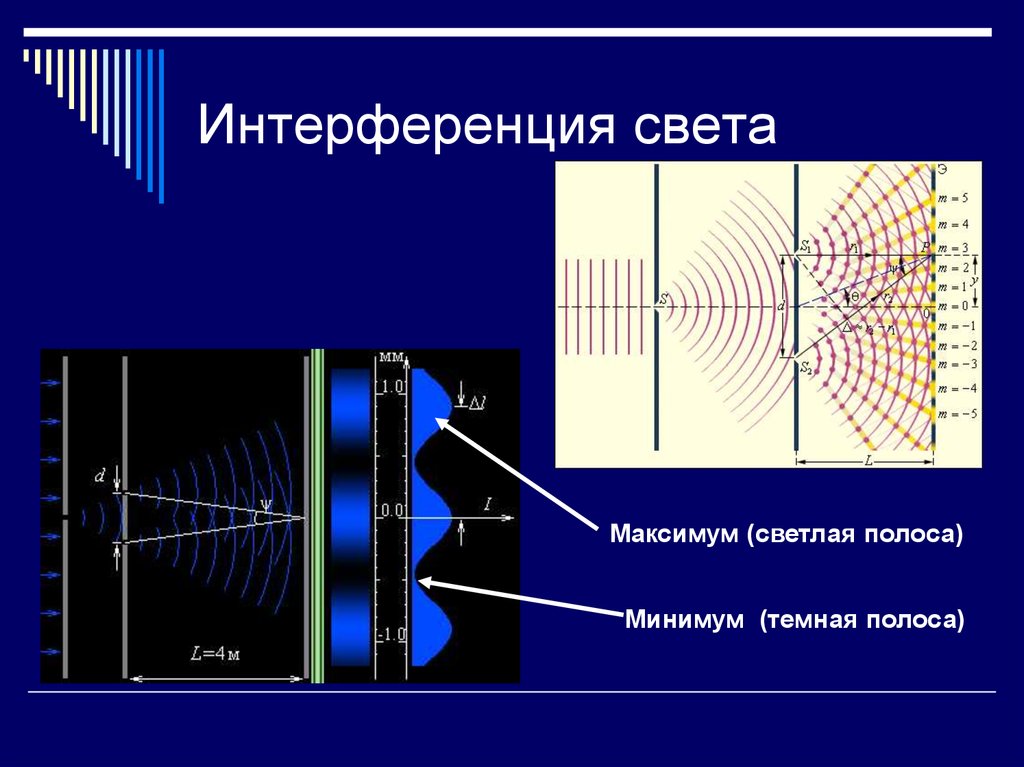
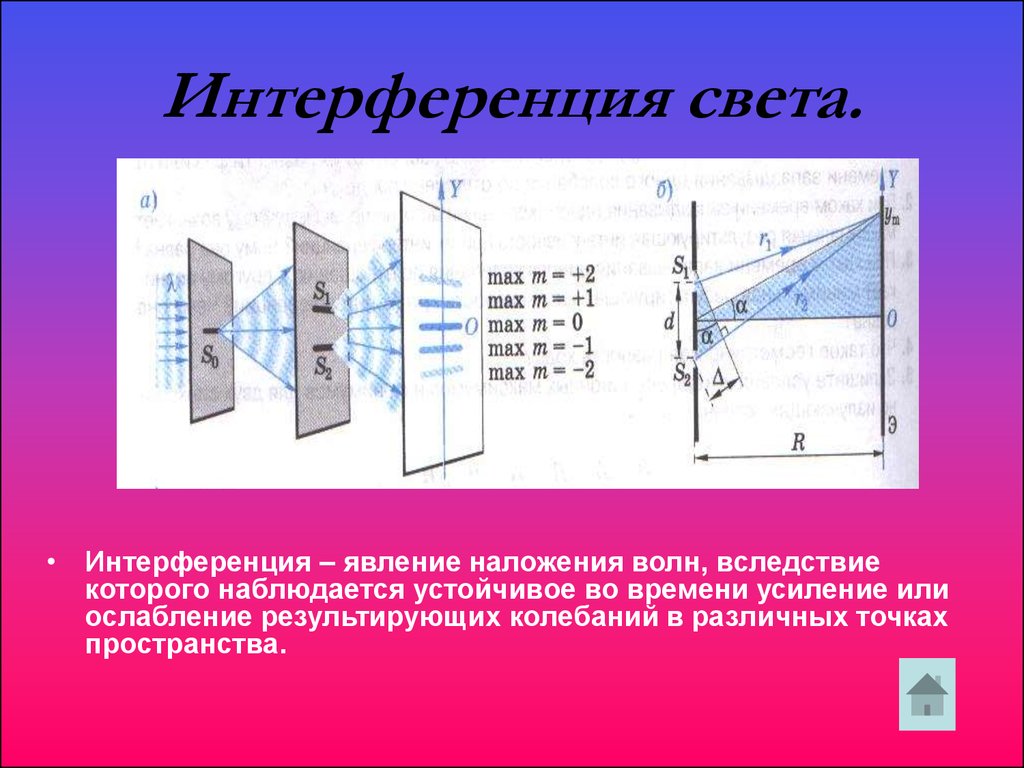
В 1801 году Томас Юнг (1773—1829 гг.), введя «принцип суперпозиции», первым дал достаточно детальное и, по сути, не отличающееся от современного объяснение этого явления и ввёл в научный обиход термин «интерференция» (1803). Он также выполнил демонстрационный эксперимент по наблюдению интерференции света, получив интерференцию от двух щелевых источников света (1802); позднее этот опыт Юнга стал классическим.
Кольца Ньютона
Основная статья: Кольца Ньютона
Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами.
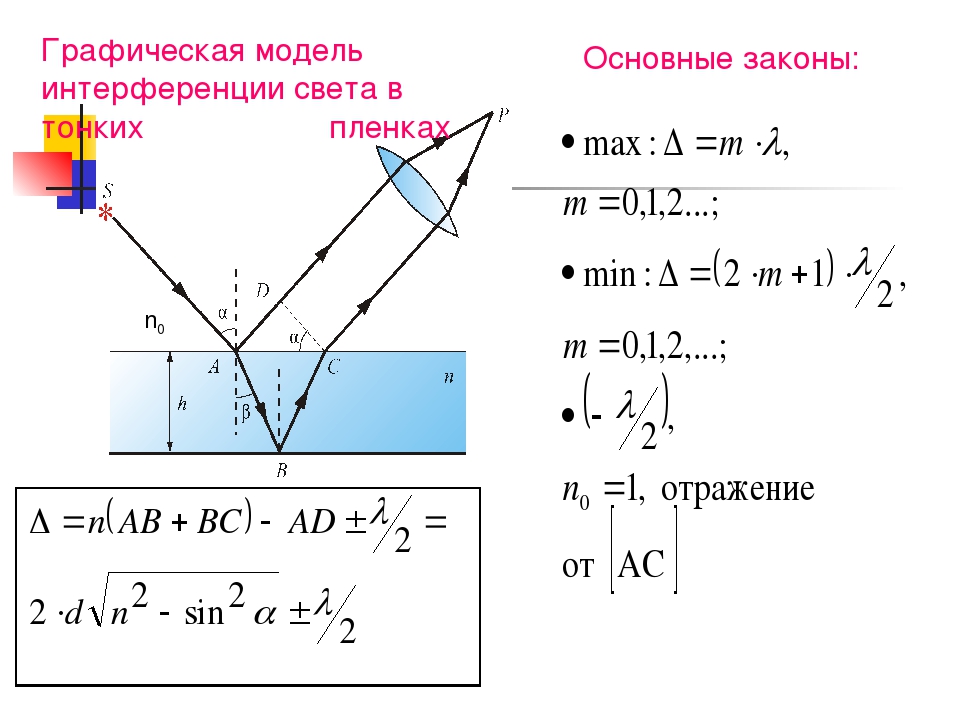
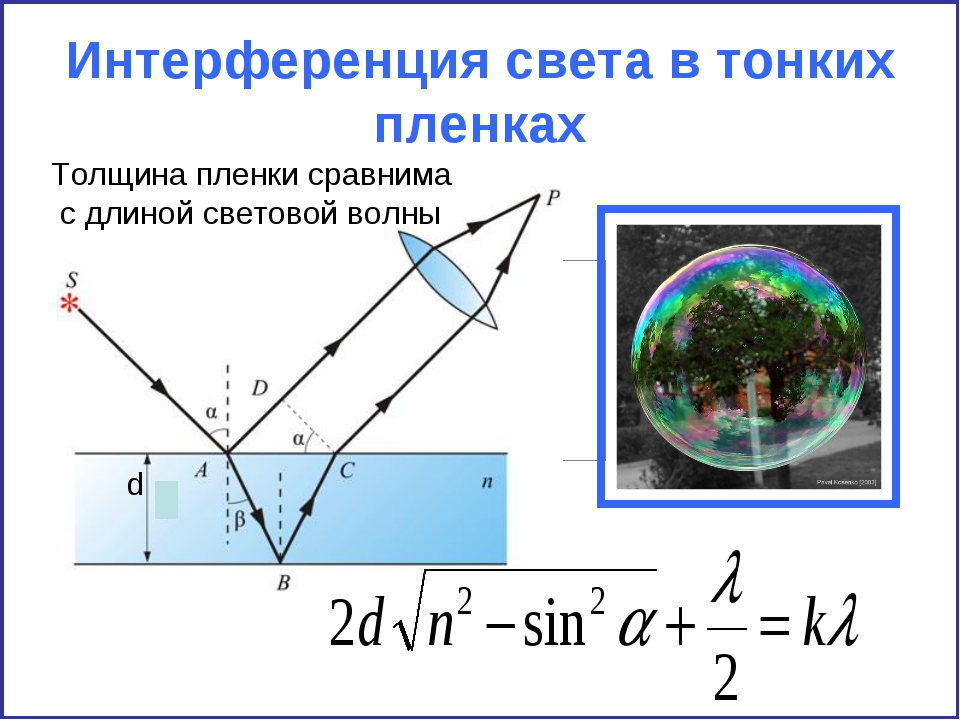
Интерференция света в тонких плёнках
основная статья:Интерференция в тонких плёнках

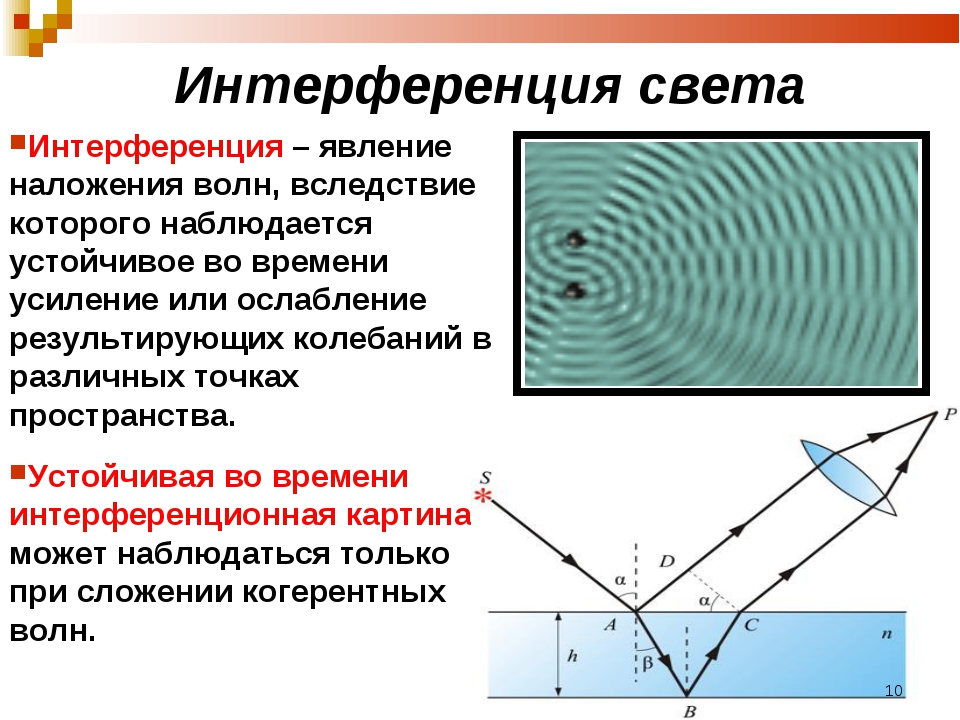
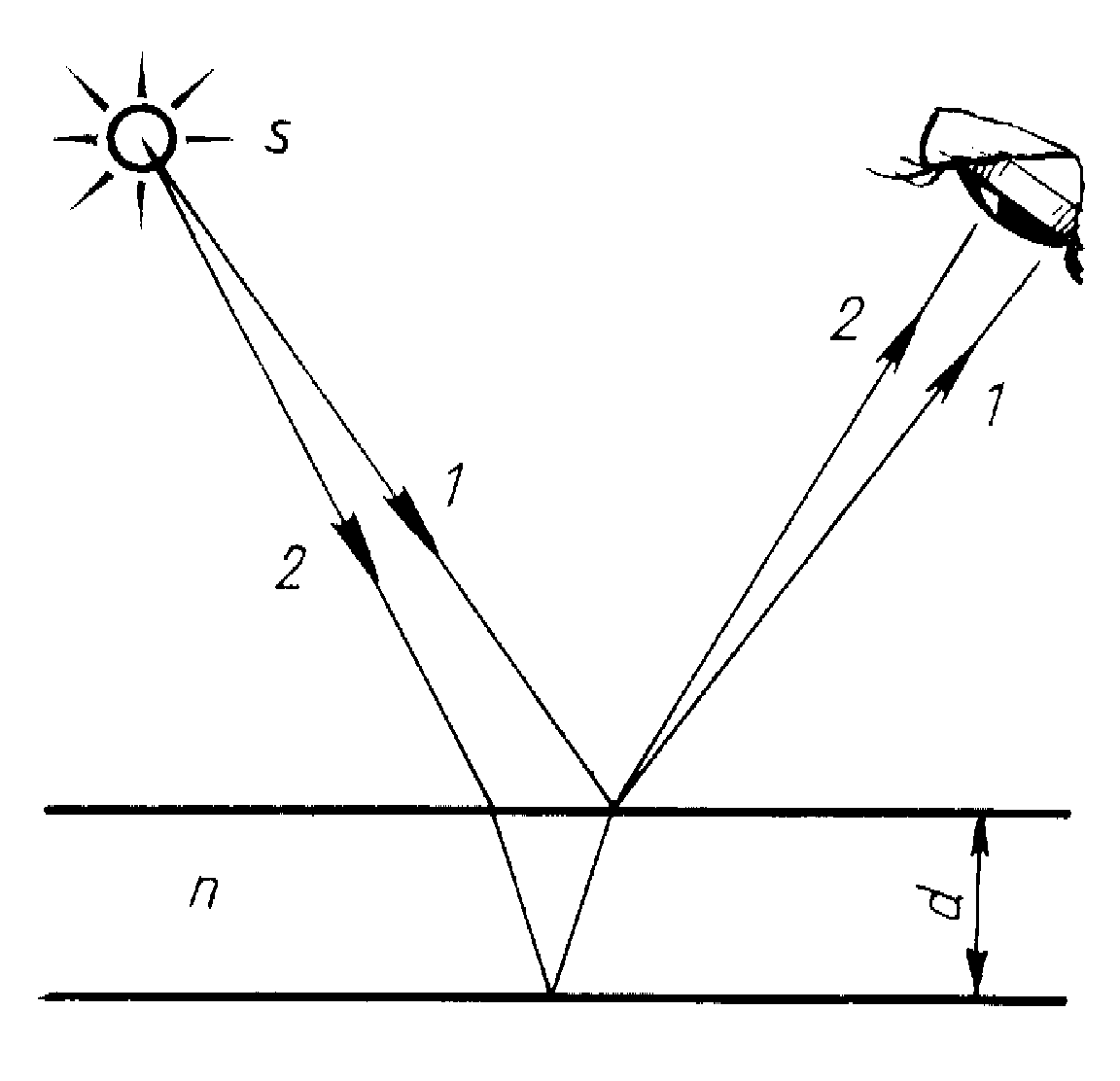
Интерференция в тонкой плёнке. Альфа — угол падения, бета — угол преломления, жёлтый луч отстанет от оранжевого, они сводятся глазом в один и интерферируют.
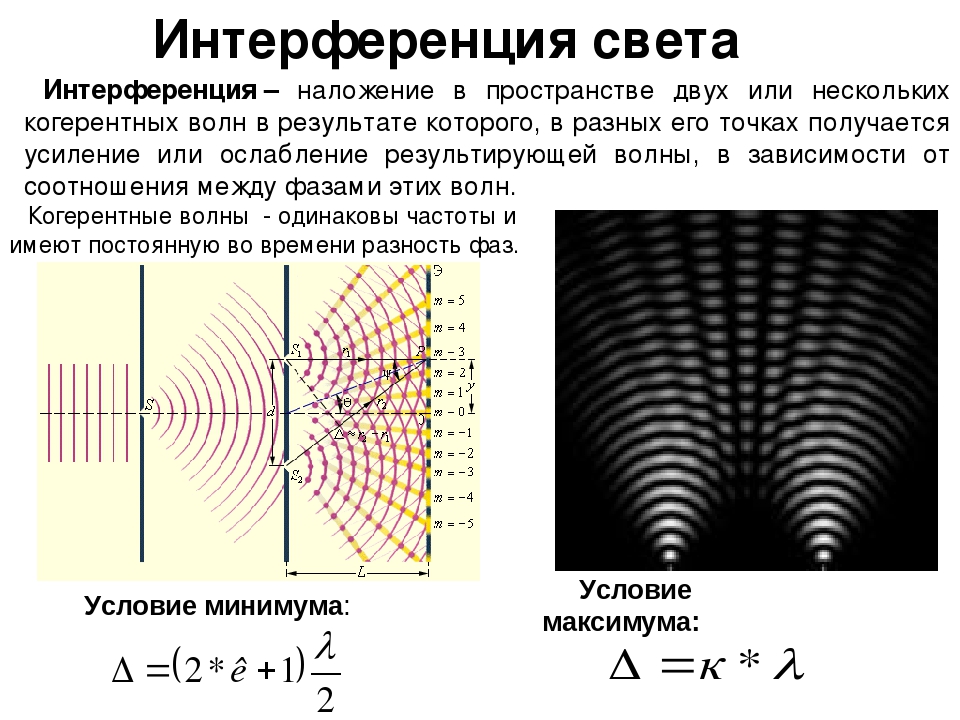
Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света длиной волны λ{\displaystyle \lambda }, падая перпендикулярно к поверхности плёнки толщиной d{\displaystyle d}, отразится дважды — от внутренней и наружной её поверхностей. Если плёнка достаточно тонка, так что её толщина не превышает длину цуга волн падающего света, то на верхней границе раздела сред отражённые лучи будут когерентны и поэтому смогут интерферировать.
Изменение фазы проходящего через плёнку луча, в общем случае, зависит от показателя преломления плёнки и окружающих её сред. Кроме того, надо учитывать, что свет при отражении от оптически более плотной среды меняет свою фазу на половину периода. Так, например, в случае для воздуха (n{\displaystyle n}1{\displaystyle 1} ≈ 1{\displaystyle 1}), окружающего тонкую масляную плёнку (n{\displaystyle n}2{\displaystyle 2} ≈ 1.5{\displaystyle 1.5}), луч, отражённый от внешней поверхности будет иметь сдвиг фазы π{\displaystyle \pi }, а от внутренней — не будет. Интерференция будет конструктивной, если итоговая разница между пройденными этими лучами путями на поверхности плёнки будет составлять полуцелое число длин волн в плёнке λ{\displaystyle \lambda }2{\displaystyle 2}=λ{\displaystyle =\lambda }1{\displaystyle 1}n1n2{\displaystyle {\frac {n_{1}}{n_{2}}}}.
То есть Δφconst=2d2πλ2+π(2k−1)=2d2πn2λ1n1+π(2k−1),k∈Z{\displaystyle \Delta \varphi _{const}=2d{\frac {2\pi }{\lambda _{2}}}+\pi (2k-1)=2d{\frac {2\pi n_{2}}{\lambda _{1}n_{1}}}+\pi (2k-1),k\in \mathbb {Z} }
Для деструктивной интерференции в данном примере необходимо, чтобы разность фаз между лучами была кратна 2π{\displaystyle 2\pi }.
То есть Δφdest=2d2πn2λ1n1+2πk,k∈Z{\displaystyle \Delta \varphi _{dest}=2d{\frac {2\pi n_{2}}{\lambda _{1}n_{1}}}+2\pi k,k\in \mathbb {Z} }
Полное гашение лучей произойдет для толщин плёнки: ddest=12λ1kn1n2{\displaystyle d_{dest}={\frac {1}{2}}\lambda _{1}k{\frac {n_{1}}{n_{2}}}}
Интерференция света на мыльном пузыре
При k=1{\displaystyle k=1} формула даёт результат ddest≈133{\displaystyle d_{dest}\approx 133} нм — и это минимальная толщина плёнки для данных условий для образования деструктивной интерференции.
Лучи соседних участков спектра по обе стороны от λ=400{\displaystyle \lambda =400} нм интерферируют не полностью и только ослабляются. Результирующее усиление одних частей спектра и ослабление других меняет окраску плёнки. Причем малейшие изменения толщины плёнки сразу же выражаются в смещении спектра наблюдаемого цвета — этот эффект легко продемонстрировать на примере с мыльным пузырём.
Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.