Хорда (геометрия)

Определение слова «Хорда» по БСЭ:

Хорда — Хорда (от греч. chorde — струна)(математическая), прямолинейный отрезок, соединяющий две произвольные точки кривой линии или поверхности.

Хорда — спинная струна, эластичная несегментированная скелетная ось у хордовых животных и человека. У некоторых оболочников (аппендикулярии), у бесчерепных (ланцетник) и некоторых позвоночных (круглоротые, из рыб — у цельноголовых, хрящевых ганондов и двоякодышащих) X. сохраняется в течение всей жизни. У остальных позвоночных и оболочников имеется только в период эмбрионального развития. у взрослых позвоночных X. заменяется позвонками. Положение X. в теле животного различно. У первично-хордовых зачаточная X. находится на спинной стороне кишечника в хоботке, у личинок оболочников — в хвостовом отделе тела. У бесчерепных и позвоночных X. располагается на спинной стороне тела, под нервной трубкой, между тяжами сегментированной туловищной мускулатуры. У ланцетника X. тянется от кончика хвоста до переднего конца тела, что, видимо, является вторичным приспособлением, связанным с необходимостью укрепления переднего конца тела при роющем образе жизни. У позвоночных головная часть X. оканчивается позади гипофиза.X. развивается из средней части крыши первичной кишки (хордомезодермы) в виде выпячивания, которое затем отшнуровывается и превращается в продольный цилиндрический тяж. Клетки зачатка X. уплощаются, затем вакуолизируются. На периферии сохраняется слой невакуолизированных клеток, богатых цитоплазмой, т. н. эпителий X., участвующий в выработке её оболочки. Сначала образуется тонкая наружная эластическая оболочка, богатая эластичными волокнами, затем (внутрь от неё) выделяется волокнистая оболочка, состоящая из коллагеновых волокон. У пластиножаберных и костистых рыб внутренняя часть волокнистой оболочки обособляется во внутреннюю эластическую оболочку.В волокнистой оболочке развиваются хрящевые тела позвонков, у цельноголовых — многочисленные известковые кольца. С развитием тел позвонков функцию X. как скелетной оси тела выполняет Позвоночник. У позвоночных X. — центрльный остов, вокруг которого развивается хрящевой или костный осевой скелет. Развивающиеся из отдельных частей позвонки сначала дополняют, а затем в большей или меньшей степени вытесняют X. Её остатки сохраняются между телами позвонков (рыбы), внутри позвонков (земноводные), полностью исчезают (птицы), сохраняются в межпозвонковых хрящах, образуя их студенистое ядро (млекопитающие). Опорные свойства X. обусловлены её упругостью и прочностью покрывающих оболочек. При волнообразных движениях тела низших позвоночных X. сгибается под действием сегментированной боковой мышцы туловища, разгибается вследствие своей упругости. Сохранение X. в эмбриогенезе высших позвоночных объясняется не только опорной функцией скелетной оси у эмбрионов, но и индуцирующим воздействием зачатка X. на формирование нервной трубки.Высушенная X. осетровых рыб под название вязиги используется в кулинарии.Н. С. Лебёдкина.

2Хорда в зоологии

Представители фауны, имеющие осевой скелет – хорду, объединены в общий тип Хордовые. У низших представитель – это эластичный тяж, который в процессе эволюции, у высших представителей животного мира, приобретает совершенную форму – позвоночник. У простейших хорда остается на всю жизнь. У высших хордовых эластичный тяж присутствует в зародышевой стадии или сохраняется частично в скелете.

В школьной программе хорду изучают на примере примитивного представителя хордовых – ланцетника.

Спинной тяж для простейшего животного, является опорой для внутренних органов, участвует в процессе движения вместе с примитивными мышцами. Над хордой ланцетника находится нервная трубка, из ее переднего отдела у высших организмов формируется головной мозг, из заднего отдела спинной. Из самой хорды формируется позвоночник, сегментированный на позвонки и отделы, выполняющие определенную функцию. Животные, у которых хорда сохранилась на всю жизнь – это ланцетник и представители некоторых отрядов рыб:

круглоротые
двоякодышащие
хрящевые
осетровые

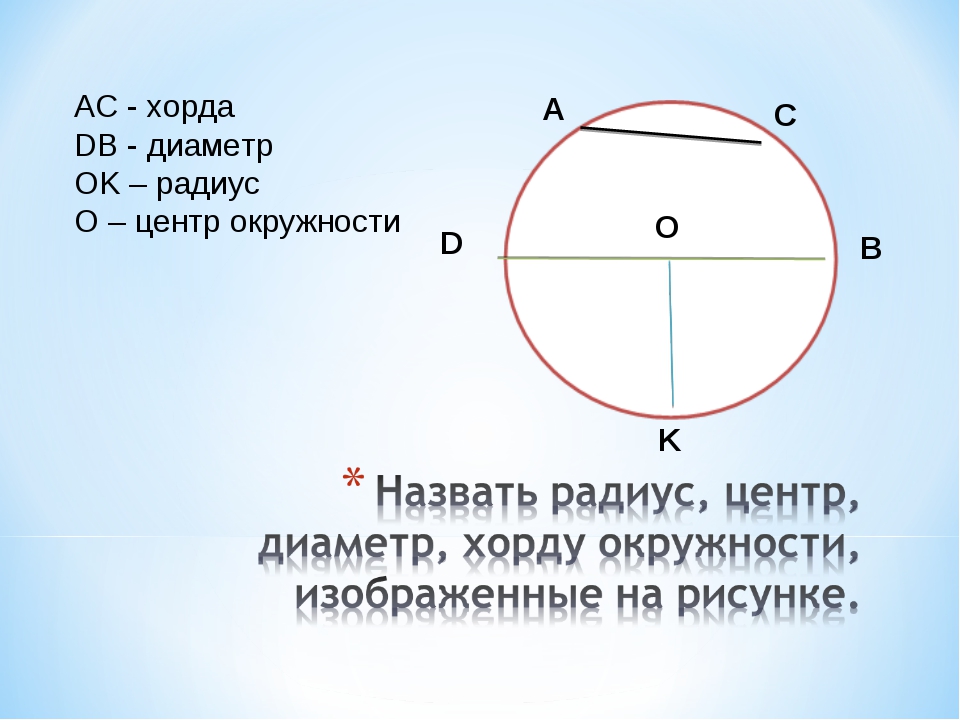
Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.

Взаимодействия с дугой

Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:

Две равные между собой хорды стягивают равные дуги.
Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.

Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.

Хорда и радиус

Между этими понятиями существуют следующие связи:

Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Как построить геометрическую хорду

Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.

Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.

Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.

1Хорда в геометрии

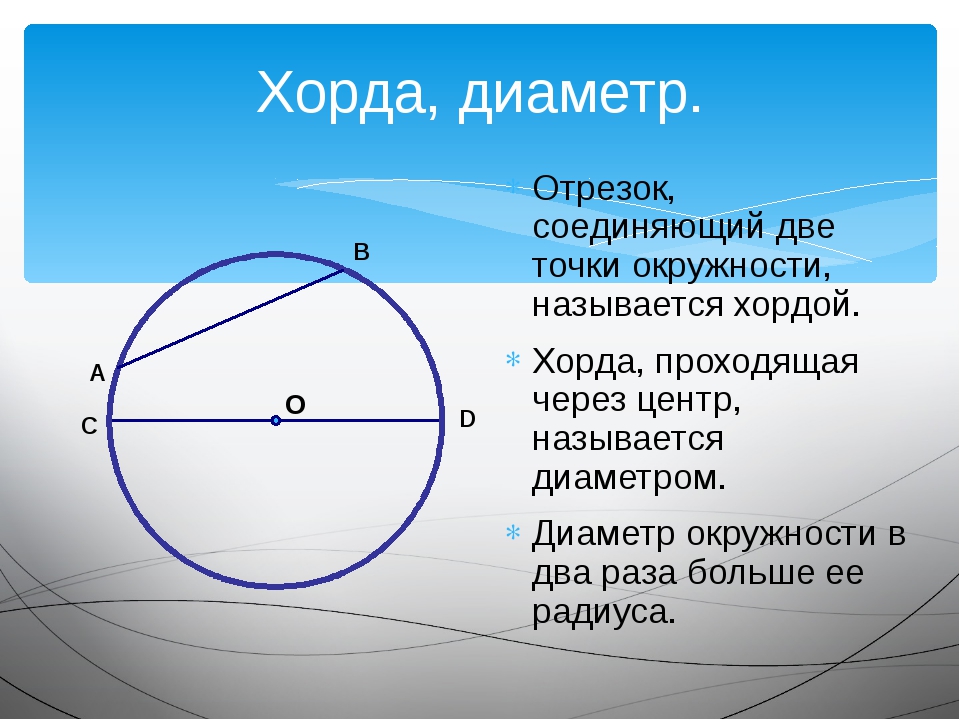
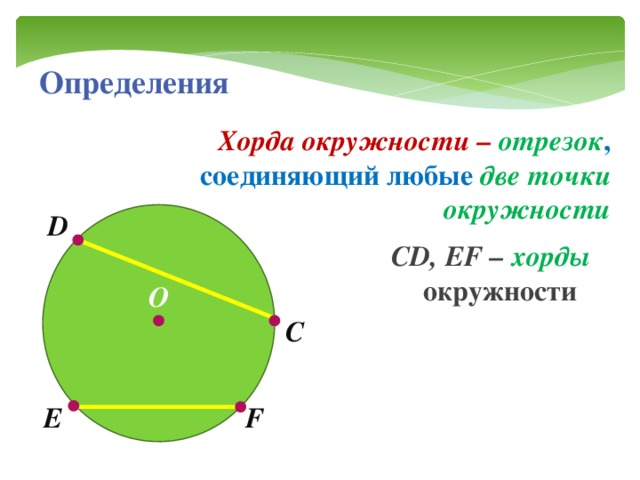
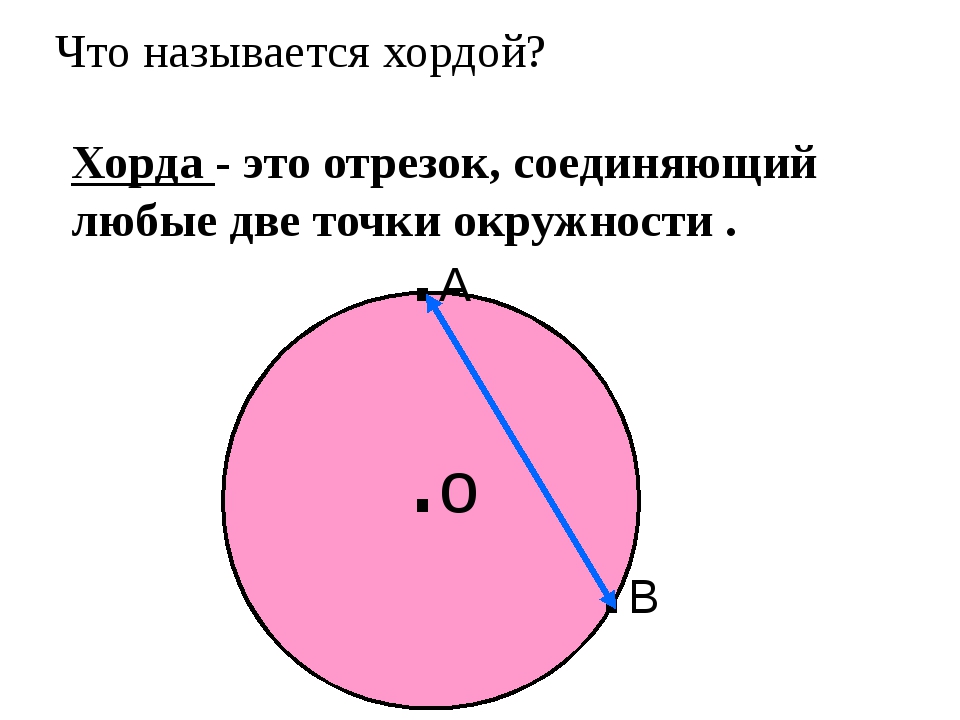
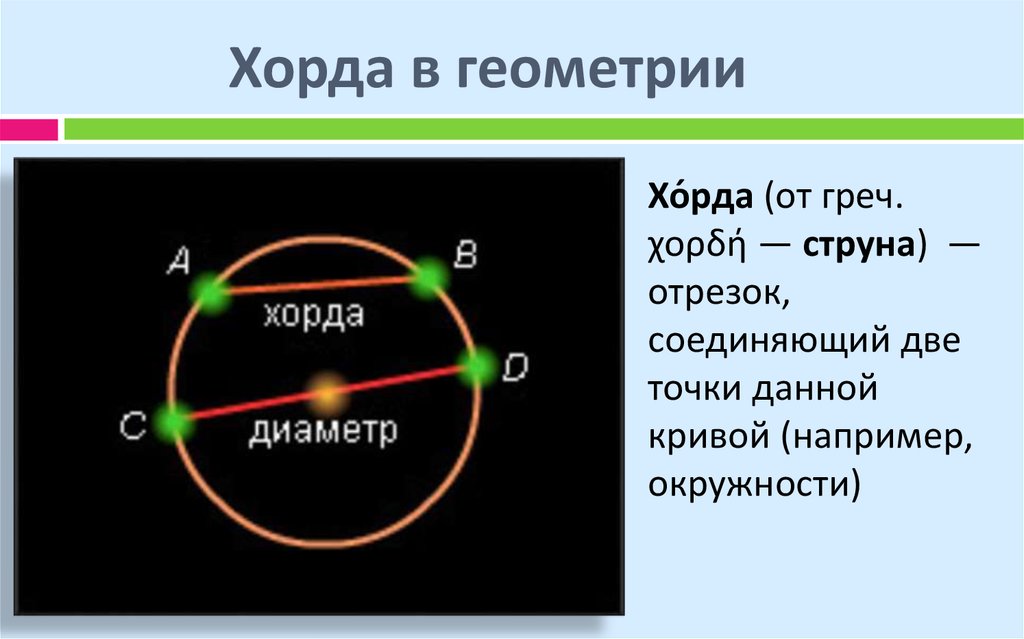
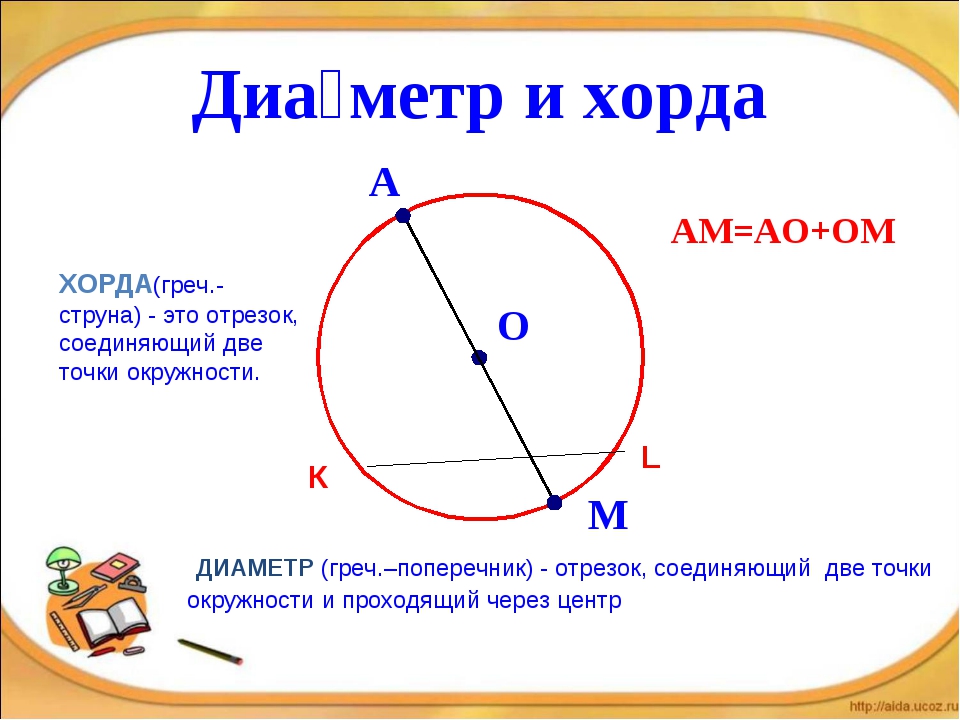
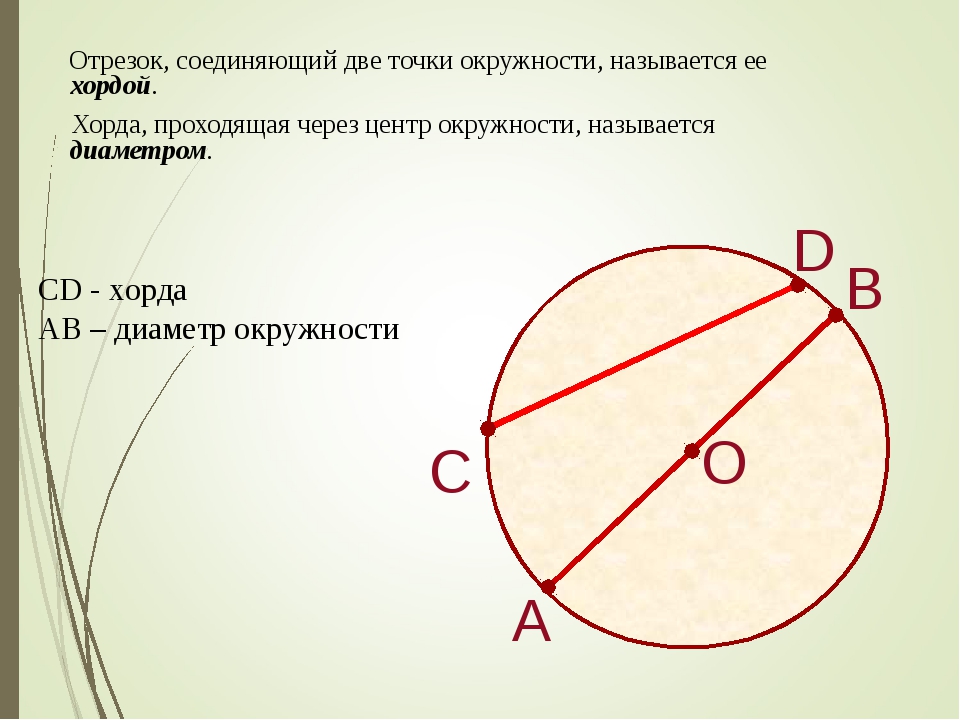
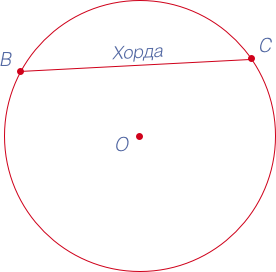
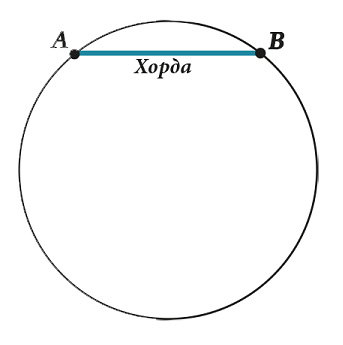
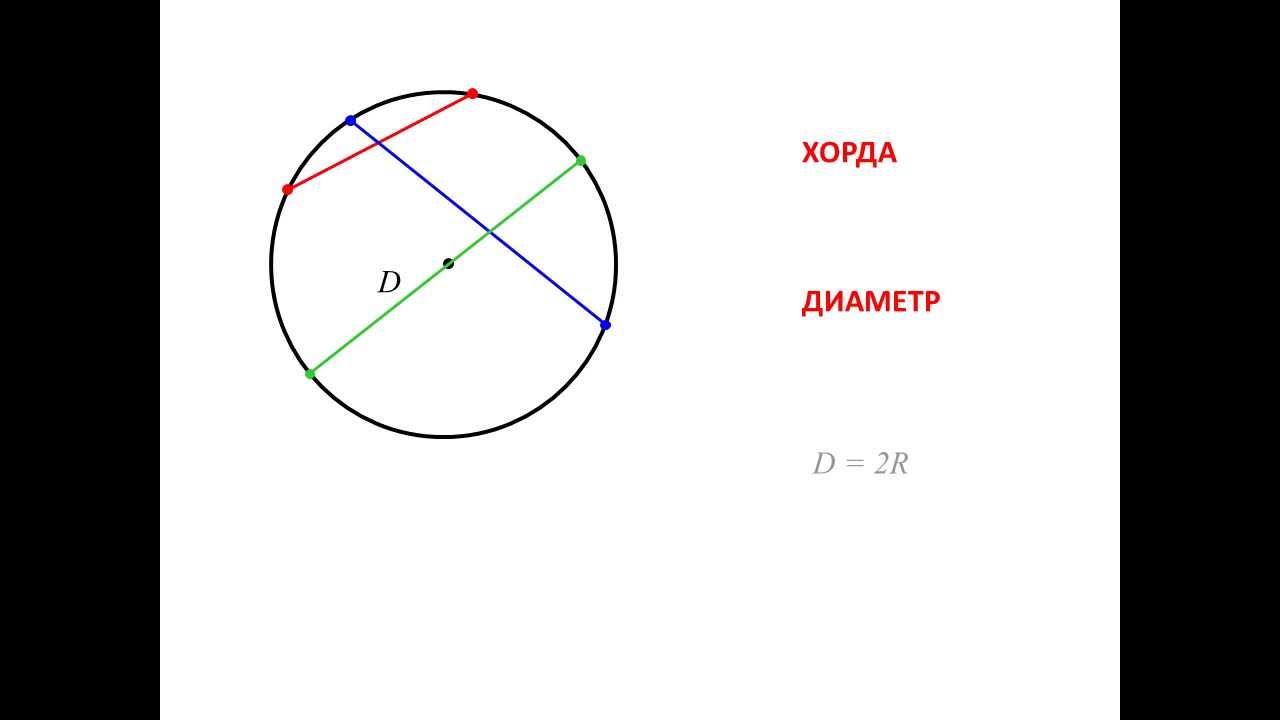
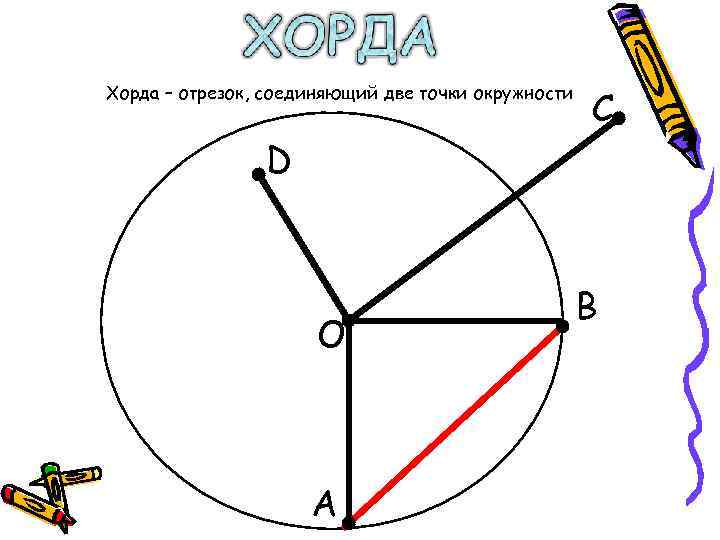
Хорда в геометрии – это отрезок, соединяющий две точки на окружности.

Для построения хорды необходимо:

начертить окружность
отметить на ней две точки
соединить их прямой линией

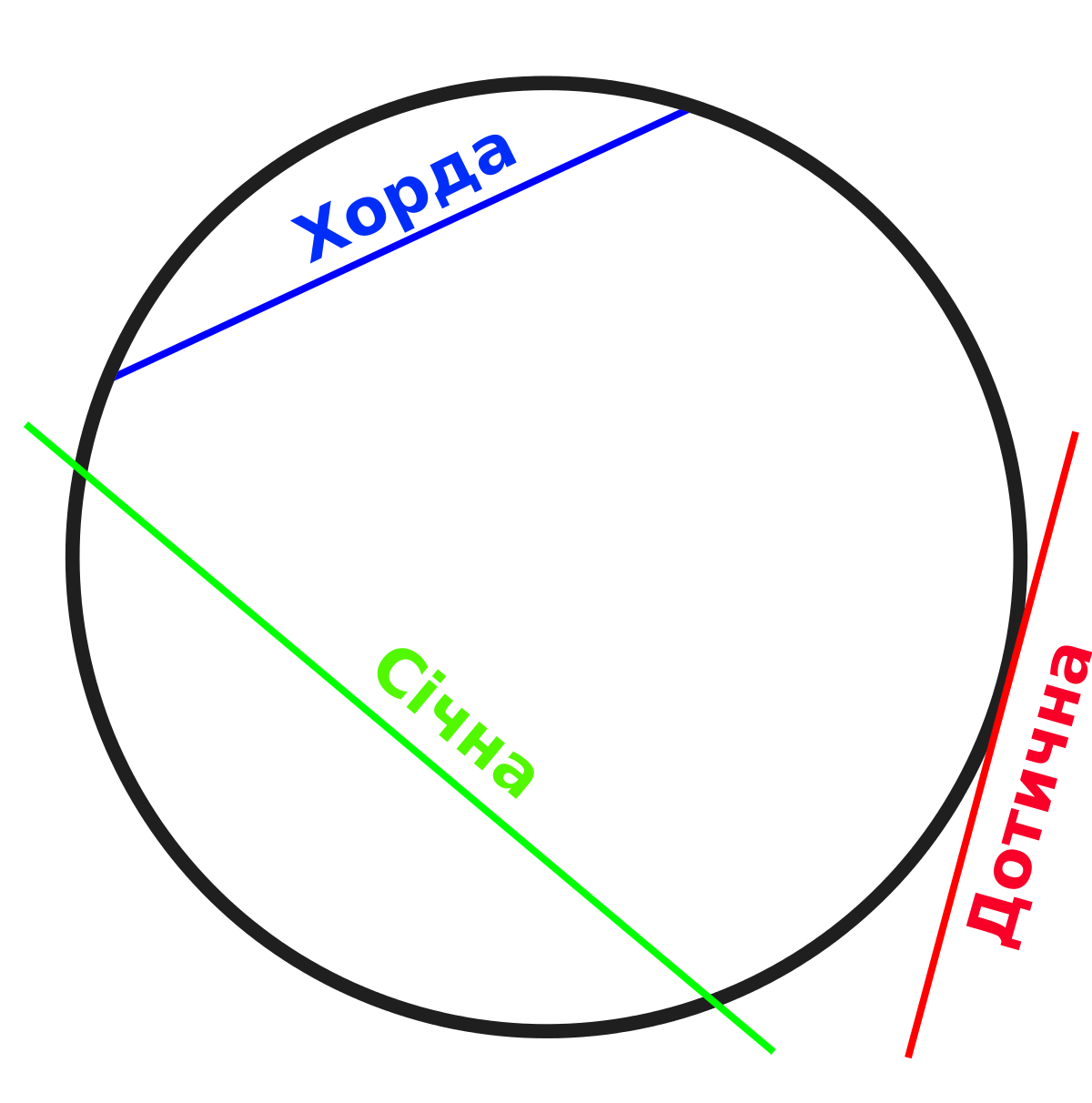
Хорда, выходящая за периметр окружности, называется секущей.

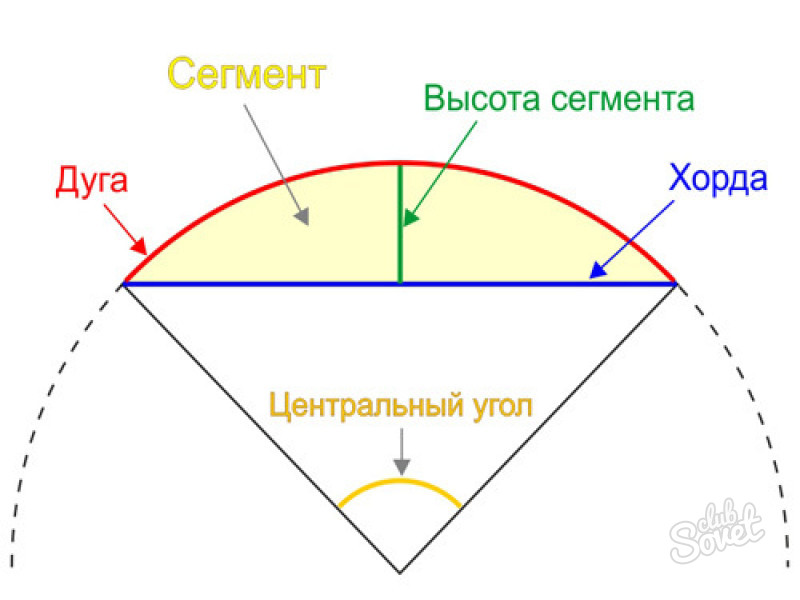
Геометрическая фигура между хордой и окружностью называется сегментом, а дуга окружности между двумя точками на ней называется дугой. Самая большая хорда – это диаметр, он соединяет две точки на окружности и проходит через центр. Две хорды, выходящие из одной точки на окружности, образуют вписанный угол, а диаметр развернутый.

В планиметрии хорда является секущим отрезком, проходящим по кривой линии и пересекающим ее в нескольких точках. Это может быть не только окружность, но и эллипс, гипербола, парабола. Свойства хорды и секущей используют в градостроении. Чтобы соединить два района или области сокращают расстояние и строят дороги, соединяя кривую хордой или секущей.

Свойства хорды используются в авиастроении. Существует термин “линия хорды” – отрезок, соединяющий самые удаленные точки профиля крыла. При конструировании летательных аппаратов учитывается средняя аэродинамическая хорда профиля.

Свойства хорд окружности

Если хорда AD{\displaystyle AD} равна хорде BC{\displaystyle BC}, то дуга AD{\displaystyle AD} равна дуге BC{\displaystyle BC}. Если хорда AD{\displaystyle AD} параллельна хорде BC{\displaystyle BC}, то дуга AB{\displaystyle AB} равна дуге CD{\displaystyle CD}

Хорда и расстояние до центра окружности

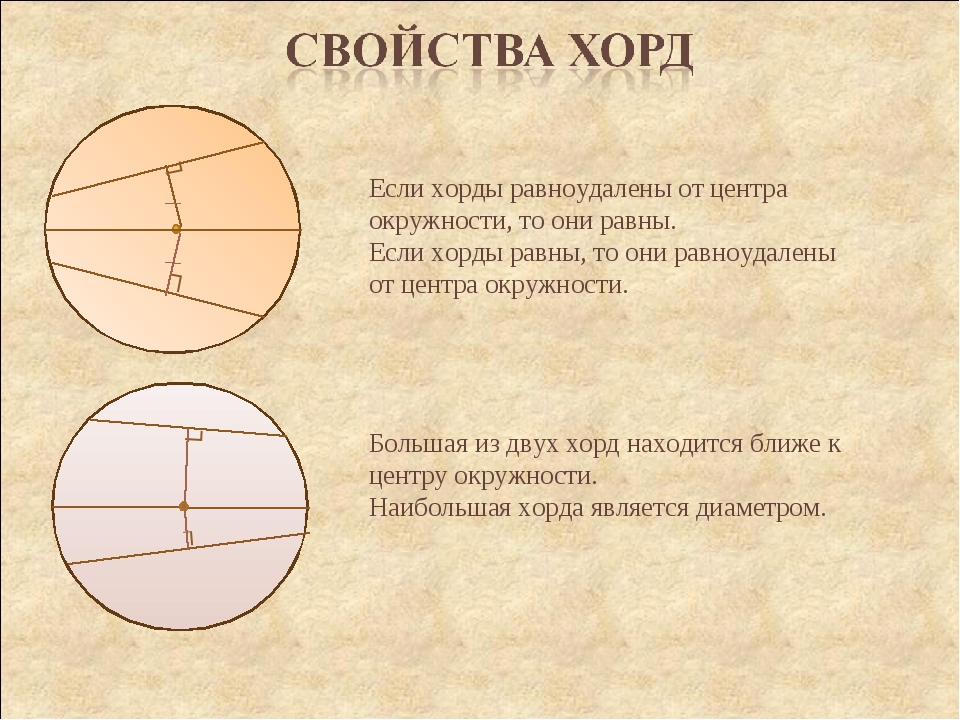
Если расстояния от центра окружности до хорд равны, то эти хорды равны.
Если хорды равны, то расстояния от центра окружности до этих хорд равны.
Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше.
Если расстояние от центра окружности до хорды меньше, то эта хорда больше. Если расстояние от центра окружности до хорды больше, то эта хорда меньше.
Наибольшая возможная хорда является диаметром.
Наименьшая возможная хорда является точкой.
Если хорда проходит через центр окружности, то эта хорда является диаметром.
Если расстояние от центра окружности до хорды равно радиусу, то эта хорда является точкой.
Серединный перпендикуляр к хорде проходит через центр окружности.

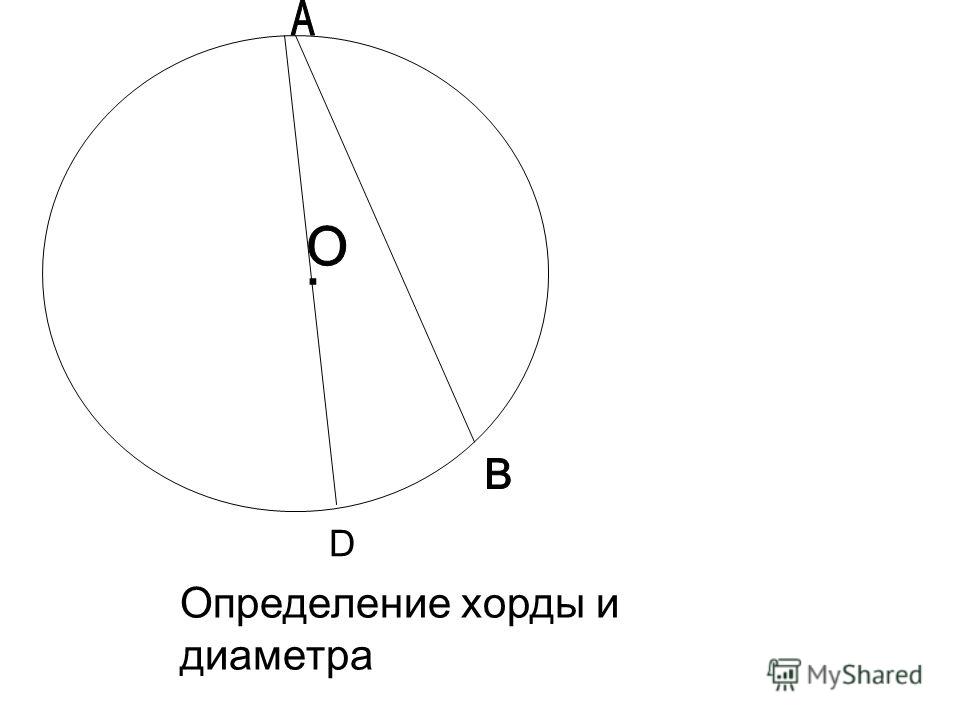
Хорда и диаметр

Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде.
Если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам.
Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
Если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу.
Если диаметр перпендикулярен хорде, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
Если диаметр делит дугу пополам, то этот диаметр перпендикулярен хорде, стягивающей эту дугу.

Хорда и радиус

Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде.
Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам.
Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
Если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
Если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

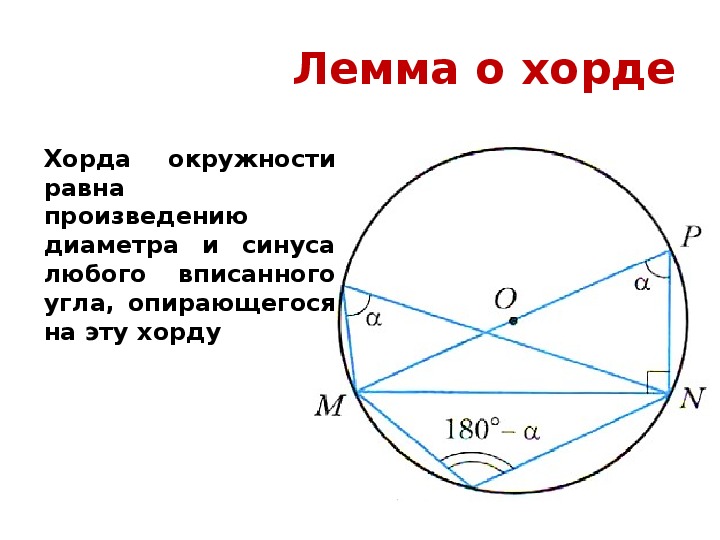
Хорда и вписанный угол

Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны.
Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла.
Если вписанный угол опирается на диаметр, то этот угол является прямым.

Хорда и центральный угол

Если хорды стягивают равные центральные углы, то эти хорды равны.
Если хорды равны, то эти хорды стягивают равные центральные углы.
Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.

Хорда и дуга

Если хорды стягивают равные дуги, то эти хорды равны.
Если хорды равны, то эти хорды стягивают равные дуги.
Из дуг, меньших полуокружности, большая дуга стягивается большей хордой, меньшая дуга стягивается меньшей хордой.
Из дуг, меньших полуокружности, большая хорда стягивает большую дугу, меньшая хорда стягивает меньшую дугу.
Из дуг, больших полуокружности, меньшая дуга стягивается большей хордой, большая дуга стягивается меньшей хордой.
Из дуг, больших полуокружности, большая хорда стягивает меньшую дугу, меньшая хорда стягивает большую дугу.
Хорда, стягивающая полуокружность, является диаметром.
Если хорды параллельны, то дуги, заключённые между этими хордами (не путать с дугами, стягиваемыми хордами), равны.

Другие свойства

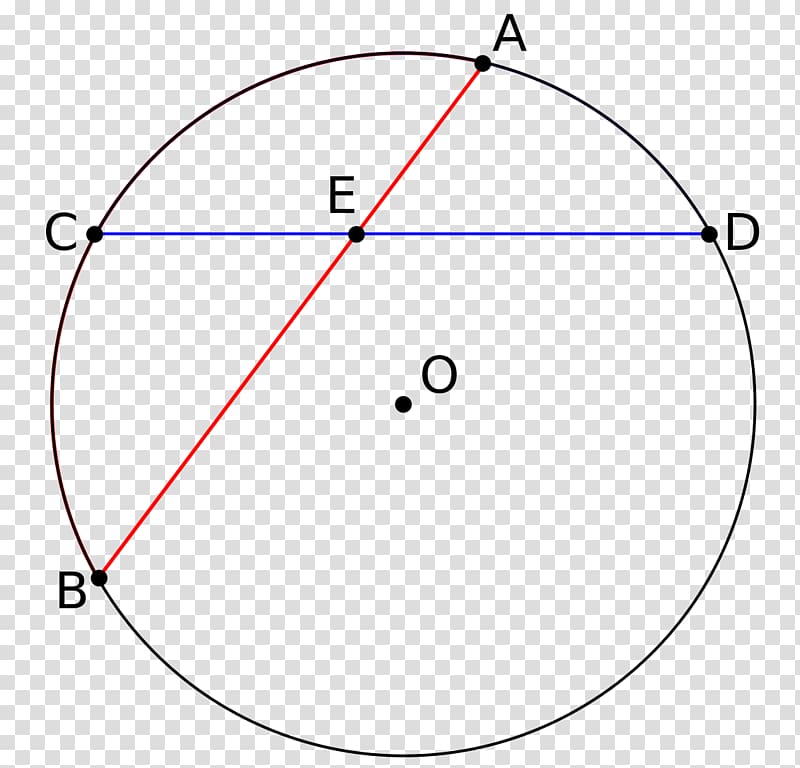
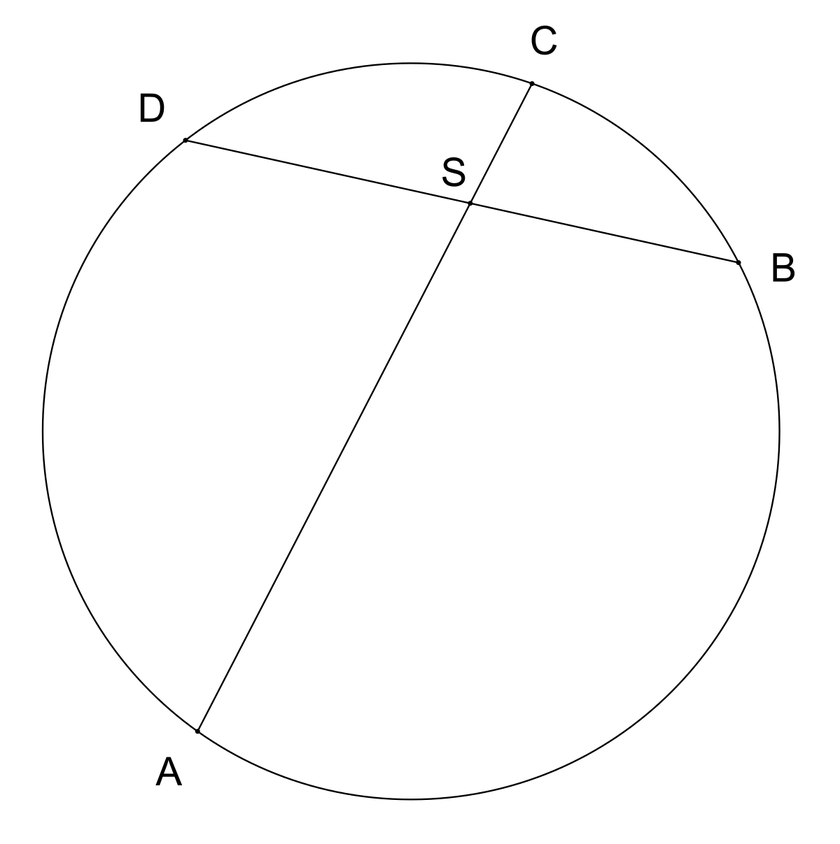
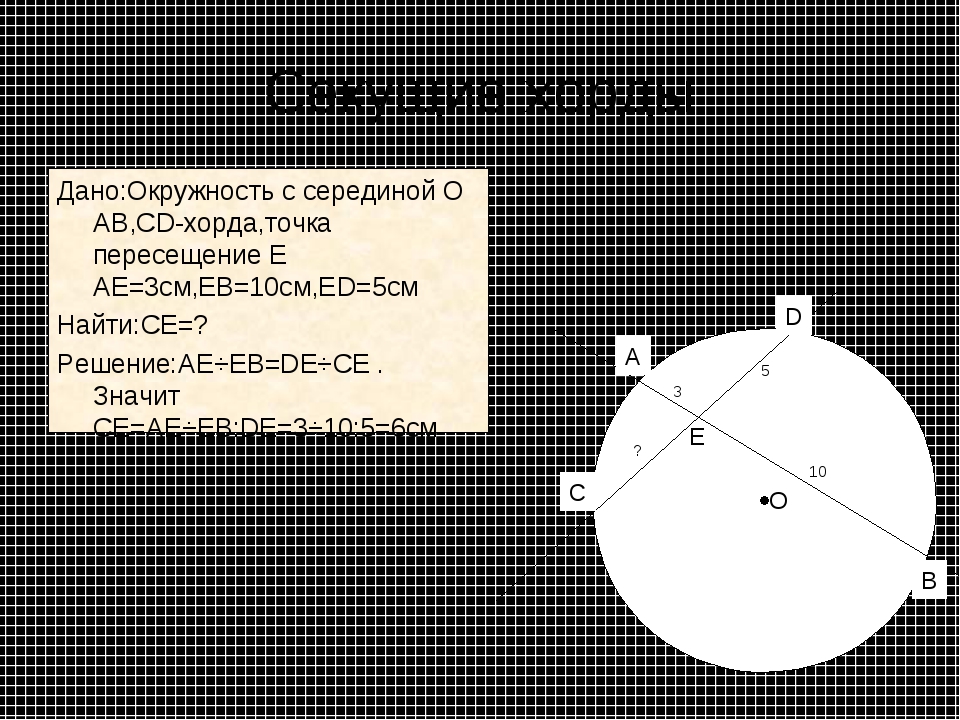
Рис. 1. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}

При пересечении двух хорд AB и CD в точке E получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. ): AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.
Если хорда делится пополам какой-либо точкой, то её длина самая маленькая по сравнению с длинами проведённых через эту точку хорд.

4Хорда в социологии

Животные, имеющие хорду самые примитивные из большого количества представителей хордовых. В социологии для объяснения наипростейшей общественной организации используется термин “хорда”, позаимствованный из животного мира. Членов общества объединяет общая цель, а задача – распределение всех благ поровну. В этом общественном строе не существует иерархии, все равны.

Если поискать в энциклопедии можно найти испанскую фамилию Хорда, немецкий суп – хорда с черносливом (подобие супа – харчо) и даже название “Хорда” скоростной линии Московского метрополитена. Спортивное оружие – лук имеет тетиву, которую часто называют хордой. Одно слово имеет несколько значений, не всегда связанных друг с другом по смыслу.