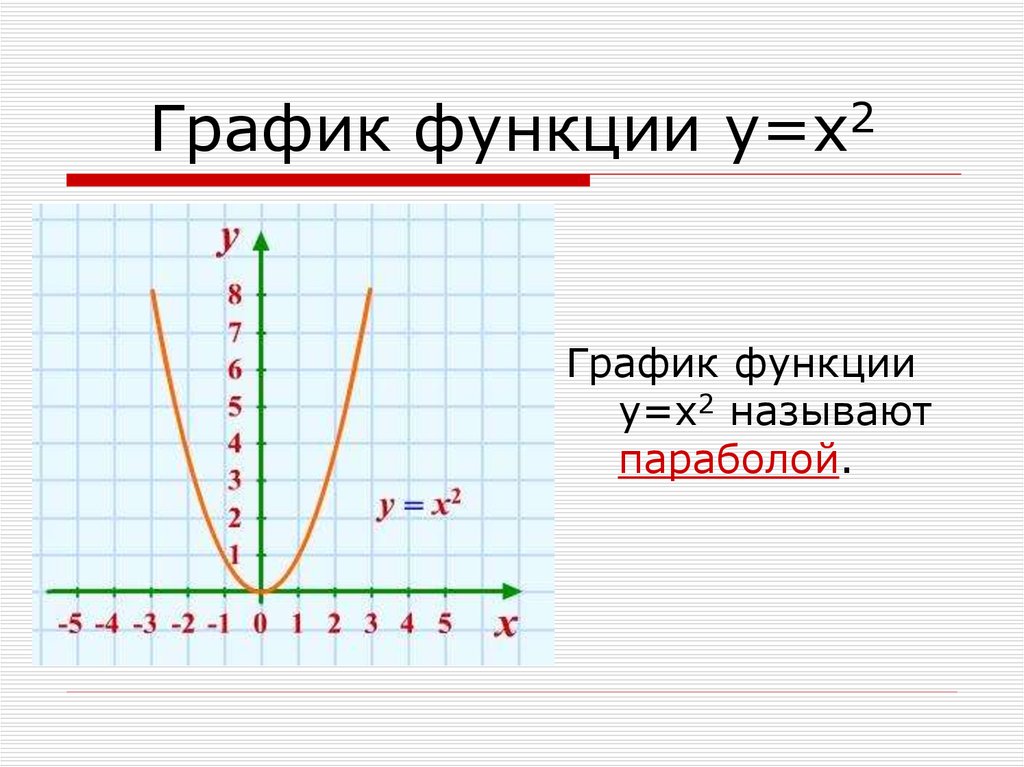
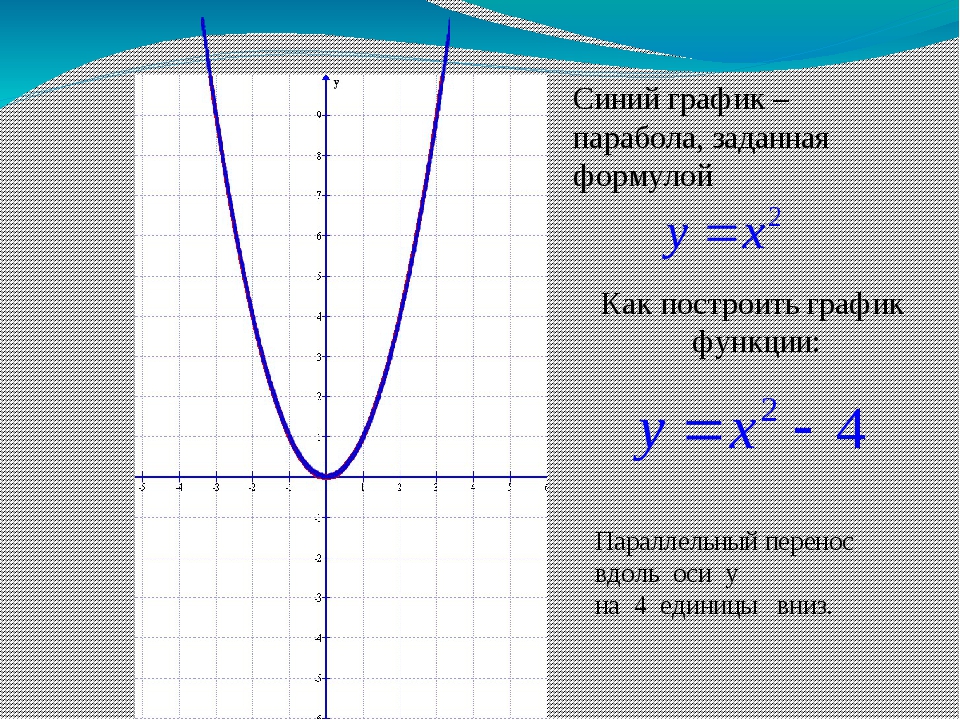
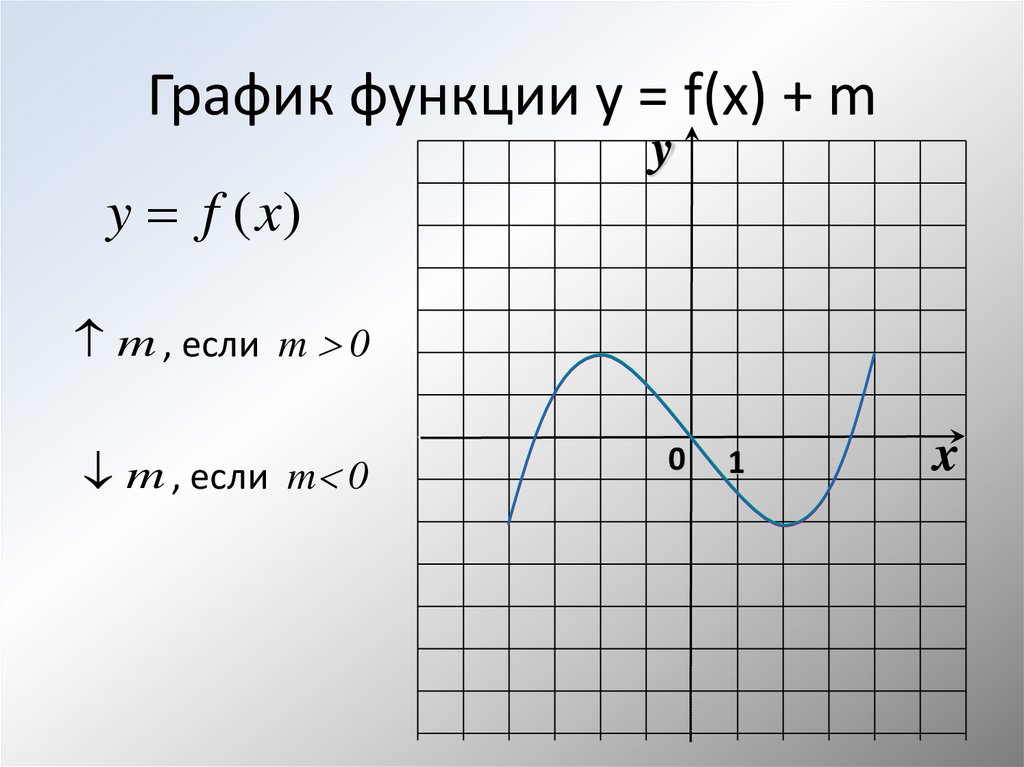
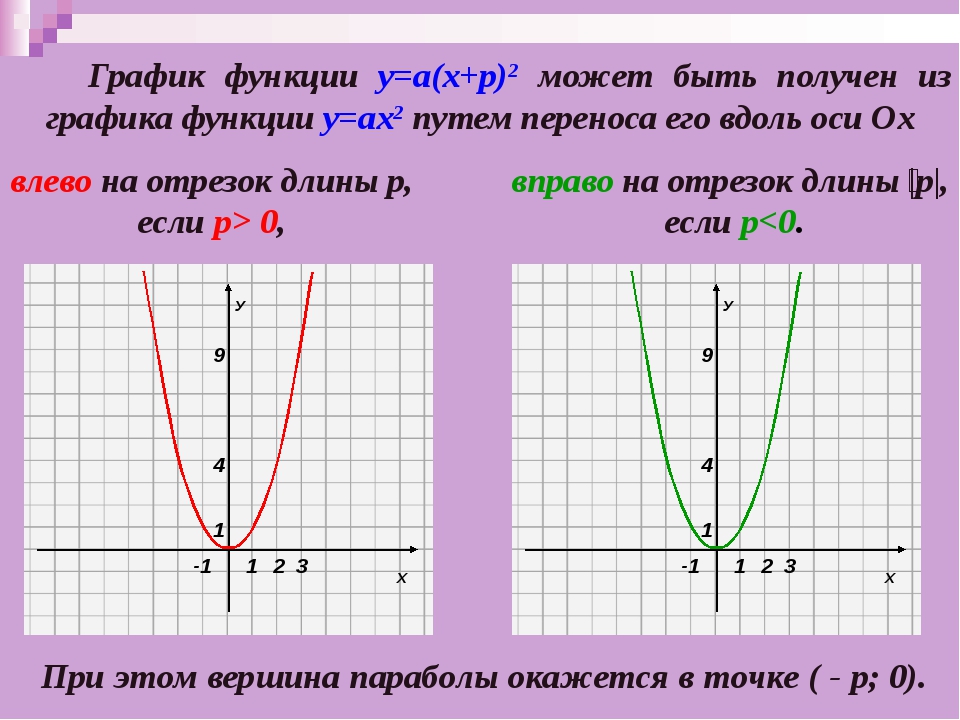
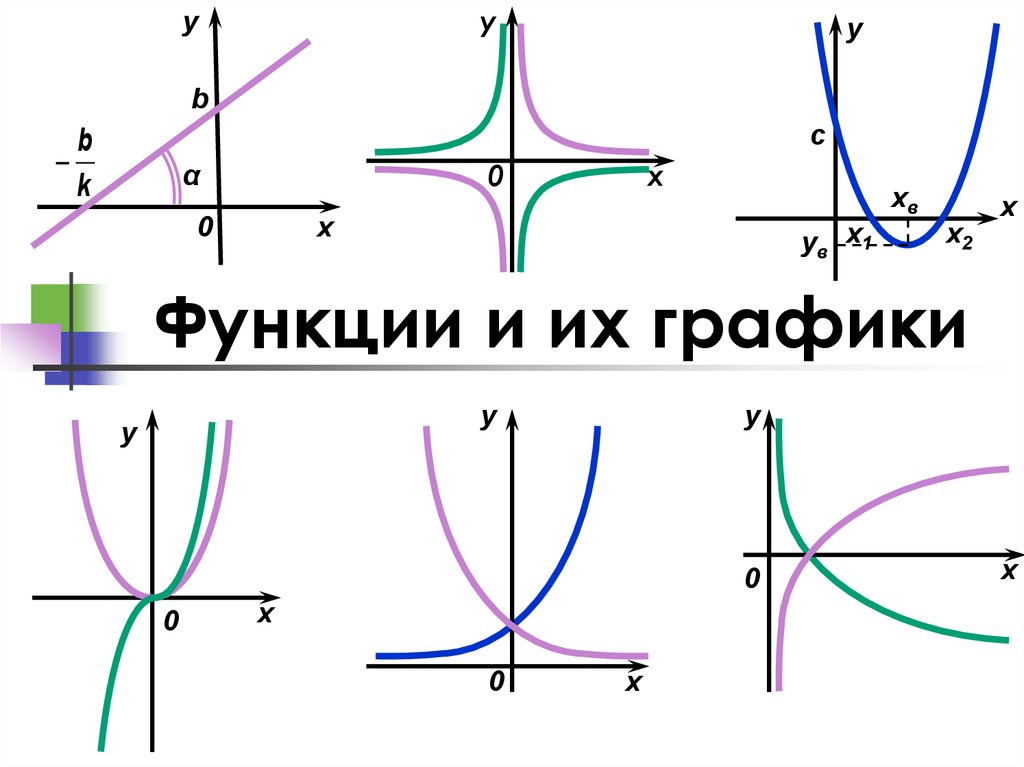
Примеры
| Функция | График функции | Описание |
|---|---|---|
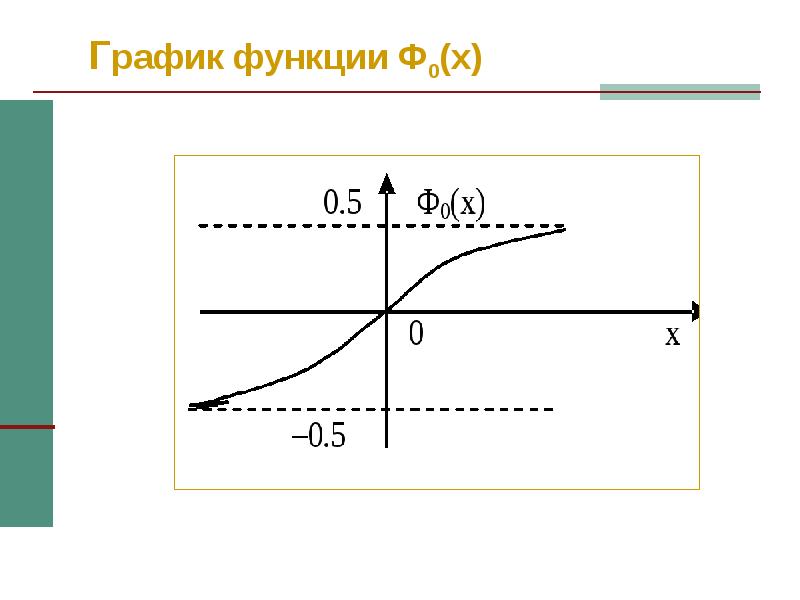
| f(x)={−1,x<,x=1,x>{\displaystyle f(x)={\begin{cases}-1,&x<0\\0,&x=0\\1,&x>0\end{cases}}} | Функция y=sgn(x).{\displaystyle y=\operatorname {sgn}(x).} В точке x= y={\displaystyle x=0~~y=0.} | |
| f(x)={,x=18,x=215,x=3{\displaystyle f(x)={\begin{cases}0,&x=1\\8,&x=2\\15,&x=3\end{cases}}} | Пример графика функции, определённой только в трёх точках {1,2,3}{\displaystyle \{1,2,3\}} и содержит только три точки с координатами (1,){\displaystyle (1,0)}, (2,8){\displaystyle (2,8)} и (3,15).{\displaystyle (3,15).} | |
| f(x)=sin(x){\displaystyle f(x)=\sin(x)}f(x)=cos(x){\displaystyle f(x)=\cos(x)}f(x)=tg(x){\displaystyle f(x)=\operatorname {tg} (x)}f(x)=ctg(x){\displaystyle f(x)=\operatorname {ctg} (x)}f(x)=sec(x){\displaystyle f(x)=\sec(x)}f(x)=cosec(x){\displaystyle f(x)=\operatorname {cosec} (x)} | Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса | |
| f(x)=1x{\displaystyle f(x)={\frac {1}{x}}} | График гиперболы. При x={\displaystyle x=0} претерпевает и в точке x={\displaystyle x=0} не определена. | |
| f(x)=bx{\displaystyle f(x)=b^{x}} | Графики функций y=bx{\displaystyle y=b^{x}} различными основаниями b{\displaystyle b}:
основание: 10 |
|
| f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x} | График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x} кубического многочлена вещественной переменной, это множество {(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}. |
Сдвиг графика влево/вправо вдоль оси абсцисс
Если к АРГУМЕНТУ функции добавляется константа, то происходит сдвиг (параллельный перенос) графика вдоль оси . Рассмотрим функцию и положительное число :
Правила:
1) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц влево;
2) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц вправо.
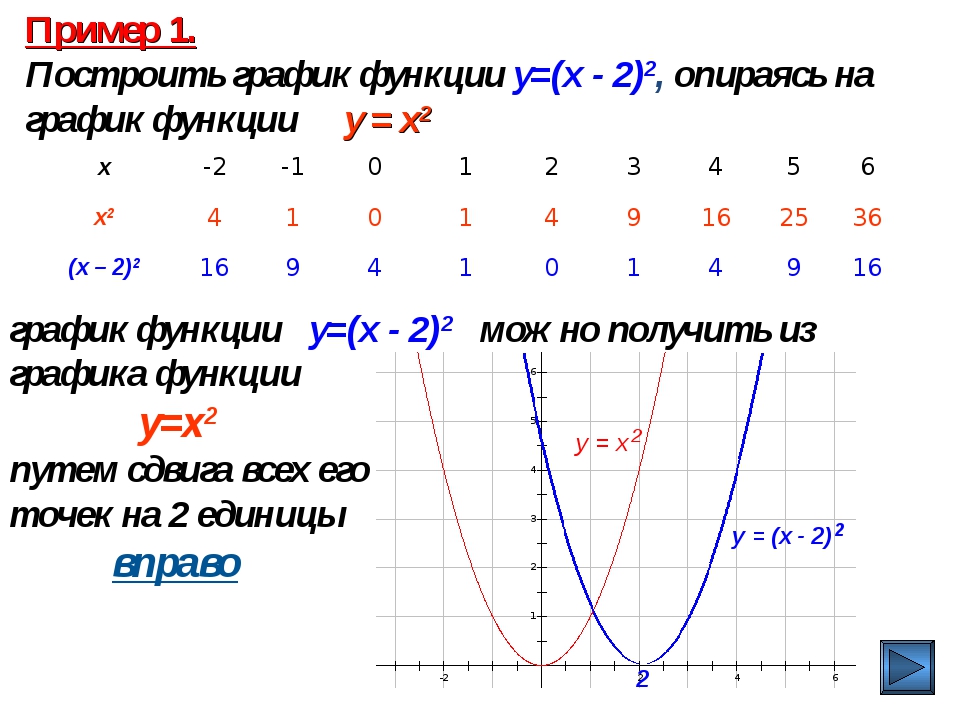
Пример 6
Построить график функции
Берём параболу и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
«Опознавательным маячком» служит значение , именно здесь находится вершина параболы .
Теперь, думаю, ни у кого не возникнет трудностей с построением графика (демонстрационный пример начала урока) – кубическую параболу нужно сдвинуть на 2 единицы влево.
Вот ещё один характерный случай:
Пример 7
Построить график функции
Гиперболу (чёрный цвет) сдвинем вдоль оси на 2 единицы влево:
Перемещение гиперболы «выдаёт» значение, которое не входит в область определения функции. В данном примере , и уравнение прямой задаёт вертикальную асимптоту (красный пунктир) графика функции (красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
Вернёмся к тригонометрическим функциям:
Пример 8
Построить график функции
График синуса (чёрный цвет) сдвинем вдоль оси на влево:
Внимательно присмотримся к полученному красному графику …. Это в точности график косинуса ! По сути, мы получили геометрическую иллюстрацию формулы приведения , и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции получается путём сдвига синусоиды вдоль оси на единиц влево (о чём уже говорилось на уроке Графики и свойства элементарных функций). Аналогично можно убедиться в справедливости любой другой формулы приведения.
Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: , при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения , а потом сдвигаем на единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
Аргумент функции необходимо представить в виде и последовательно выполнить следующие преобразования:
1) График функции сжимаем (или растягиваем) к оси (от оси) ординат: (если , то график дополнительно следует отобразить симметрично относительно оси ).
2) График полученной функции сдвигаем влево (или вправо) вдоль оси абсцисс на (!!!) единиц, в результате чего будет построен искомый график .
Пример 9
Построить график функции
Представим функцию в виде и выполним следующие преобразования: синусоиду (чёрный цвет):
1) сожмём к оси в два раза: (синий цвет);
2) сдвинем вдоль оси на (!!!) влево: (красный цвет):
Пример вроде бы несложный, а пролететь с параллельным переносом легче лёгкого. График сдвигается на , а вовсе не на .
Продолжаем расправляться с функциями начала урока:
Пример 10
Построить график функции
Представим функцию в виде . В данном случае: Построение проведём в три шага. График натурального логарифма :
1) сожмём к оси в 2 раза: ;
2) отобразим симметрично относительно оси : ;
3) сдвинем вдоль оси на (!!!) вправо: :
Для самоконтроля в итоговую функцию можно подставить пару значений «икс», например, и свериться с полученным графиком.
В рассмотренных параграфах события происходили «горизонтально» – гармонь играет, ноги пляшут влево/вправо. Но похожие преобразования происходят и в «вертикальном» направлении – вдоль оси . Принципиальное отличие состоит в том, что связаны они не с АРГУМЕНТОМ, а с САМОЙ ФУНКЦИЕЙ.
Определение графика
При рассмотрении отображения произвольного вида fX→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:
- Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}
В частности, при рассмотрении динамических систем, изображающая точка (t,f(t)){\displaystyle (t,f(t))} представляет собою график решения соответствующего дифференциального уравнения с заданными начальными условиями такой график часто называют фазовой траекторией системы.
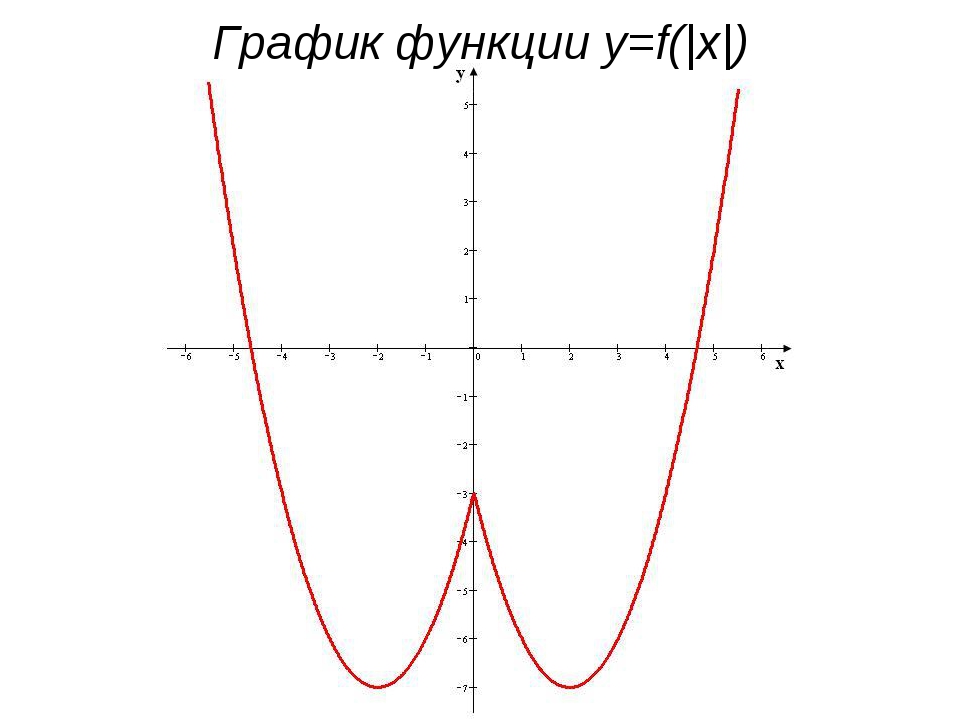
Графики функций с модулем
Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.
Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.
Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.
Правило: график функции получается из графика функции следующим образом: при график функции сохраняется, а при «сохранённая часть» отображается симметрично относительно оси .
Пример 22
Построить график функции
И снова вечная картина:
Согласно правилу, при график сохраняется:
И сохранившаяся часть отображается симметрично относительно оси в левую полуплоскость:
Действительно, функция – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.
Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:
То есть, правая волна графика задаётся функцией , а левая волна – функцией (см. Пример 13).
Пример 23
Построить график функции
Аналогично, ветвь «обычной» экспоненты правой полуплоскости отображаем симметрично относительно оси в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .
Модуль не имеет смысл «навешивать» на аргумент чётной функции: и т.п. (проанализируйте, почему).
И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.
Правило: график функции получается из графика функции следующим образом: часть графика , лежащая НАД осью сохраняется, а часть графика , лежащая ПОД осью отображается симметрично относительно данной оси.
Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)
Пример 24
Построить график функции
Сначала начертим прямую, известную широкому кругу лиц:
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси – отображается симметрично в верхнюю полуплоскость:
Модуль функции также раскрывается аналитически в кусочном виде:
Внимание! Формула отличается от формулы предыдущего пункта!
В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .
Кстати, – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и к самой функции: . Изучим более «жизненную» ситуацию:
Пример 25
Построить график функции
Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси в верхнюю полуплоскость:
Согласно формуле , распишем функцию аналитически в кусочном виде: .
Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.
На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .
Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:
Пример 26
Построить график функции .
Изобразим сами знаете что =)
И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :
Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.
Распишем функцию в кусочном виде:
Решив два простейших школьных неравенства , получаем:, где – любое целое число.
Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)
Желаю успехов!
(Переход на главную страницу)
График линейной функции
Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
Пример 1
Построить график функции . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
Если , то
Берем еще какую-нибудь точку, например, 1.
Если , то
При оформлении заданий координаты точек обычно сводятся в таблицу:
А сами значения рассчитываются устно или на черновике, калькуляторе.
Две точки найдены, выполним чертеж:
 При оформлении чертежа всегда подписываем графики.
При оформлении чертежа всегда подписываем графики.
Не лишним будет вспомнить частные случаи линейной функции:
Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых , или справа внизу между графиками
1) Линейная функция вида () называется прямой пропорциональностью. Например, . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
2) Уравнение вида задает прямую, параллельную оси , в частности, сама ось задается уравнением . График функции строится сразу, без нахождения всяких точек. То есть, запись следует понимать так: «игрек всегда равен –4, при любом значении икс».
3) Уравнение вида задает прямую, параллельную оси , в частности, сама ось задается уравнением . График функции также строится сразу. Запись следует понимать так: «икс всегда, при любом значении игрек, равен 1».
Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде или .
Построение прямой – самое распространенное действие при выполнении чертежей.
Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.