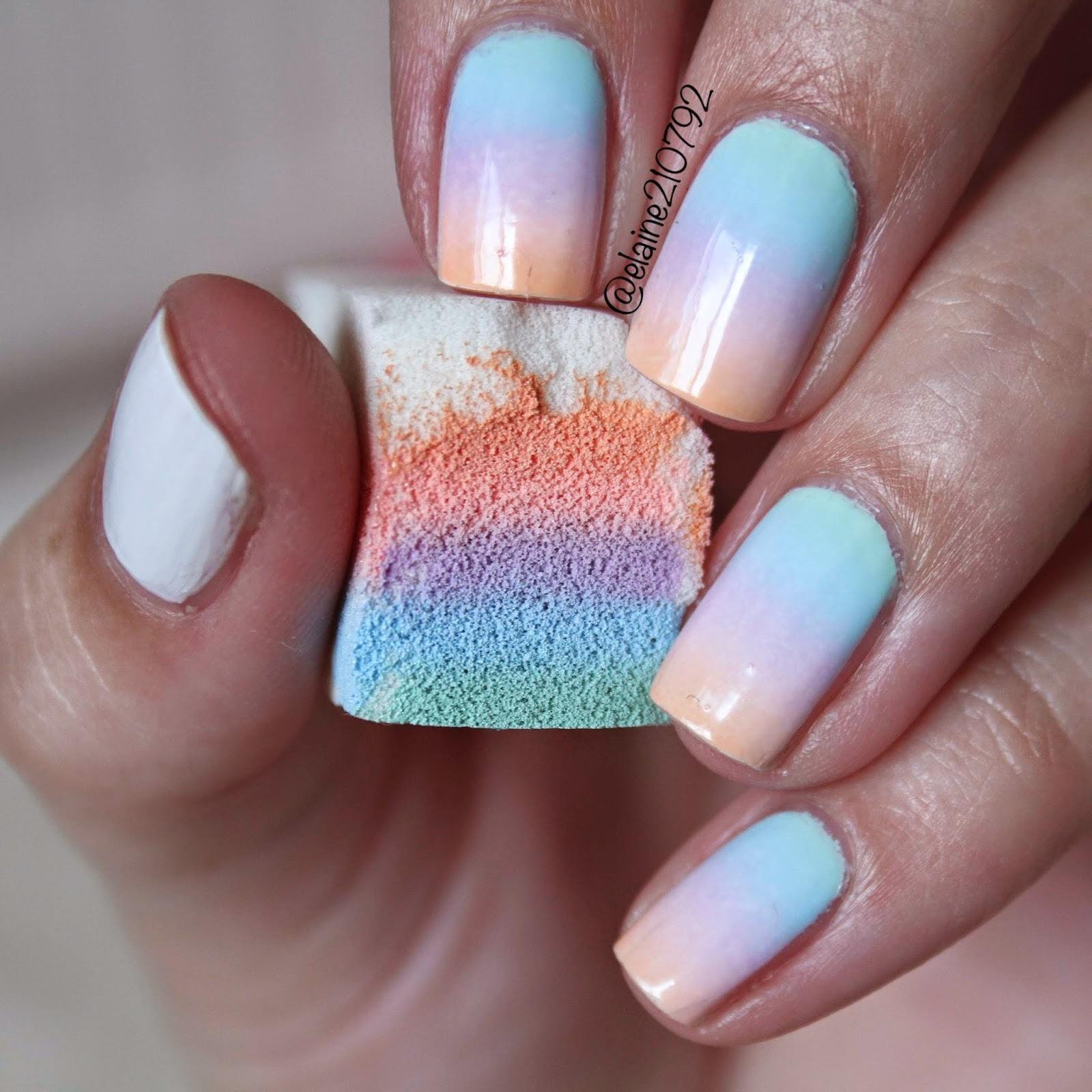Что такое градиент? виды градиентов

Градиентная красота

Для посетительниц салонов красоты вопрос о том, что такое градиент, не станет неожиданным. Правда, и в этом случае знание математических законов и основ физики не обязательно. Речь идет все так же о цветовых переходах. Объектом градиента становятся волосы и ногти. Техника омбрэ, что в переводе с французского обозначает «тон» пришла в моду от спортивных любительниц серфинга и других пляжных развлечений. Естественным образом выгоревшие и вновь отросшие волосы стали хитом. Модницы стали специально окрашивать волосы с еле заметным переходом оттенков.

Техника омбре не прошла мимо маникюрных салонов. Градиент на ногтях создает окраску с постепенным осветлением пластины от корня к краю. Мастера предлагают горизонтальный, вертикальный, с переходом и другие разновидности.

Градиент в ортогональных криволинейных координатах

gradU(q1,q2,q3)=1H1∂U∂q1e→1+1H2∂U∂q2e→2+1H3∂U∂q3e→3,{\displaystyle \operatorname {grad} \,U(q_{1},\;q_{2},\;q_{3})={\frac {1}{H_{1}}}{\frac {\partial U}{\partial q_{1}}}{\vec {e}}_{1}+{\frac {1}{H_{2}}}{\frac {\partial U}{\partial q_{2}}}{\vec {e}}_{2}+{\frac {1}{H_{3}}}{\frac {\partial U}{\partial q_{3}}}{\vec {e}}_{3},}

где Hi{\displaystyle H_{i}} — .

Полярные координаты (на плоскости)

Коэффициенты Ламе:

H1=1H2=r.{\displaystyle {\begin{matrix}H_{1}=1\\H_{2}=r\end{matrix}}.}

Отсюда:

gradU(r,θ)=∂U∂rer→+1r∂U∂θeθ→.{\displaystyle \operatorname {grad} \,U(r,\;\theta )={\frac {\partial U}{\partial r}}{\vec {e_{r}}}+{\frac {1}{r}}{\frac {\partial U}{\partial \theta }}{\vec {e_{\theta }}}.}

Цилиндрические координаты

Коэффициенты Ламе:

H1=1H2=rH3=1.{\displaystyle {\begin{matrix}H_{1}=1\\H_{2}=r\\H_{3}=1\end{matrix}}.}

Отсюда:

gradU(r,θ,z)=∂U∂rer→+1r∂U∂θeθ→+∂U∂zez→.{\displaystyle \operatorname {grad} \,U(r,\;\theta ,\;z)={\frac {\partial U}{\partial r}}{\vec {e_{r}}}+{\frac {1}{r}}{\frac {\partial U}{\partial \theta }}{\vec {e_{\theta }}}+{\frac {\partial U}{\partial z}}{\vec {e_{z}}}.}

Сферические координаты

Коэффициенты Ламе:

H1=1H2=rH3=rsin⁡θ.{\displaystyle {\begin{matrix}H_{1}=1\;\;\;\;\;\;\\H_{2}=r\;\;\;\;\;\;\\H_{3}=r\sin {\theta }\end{matrix}}.}

Отсюда:

gradU(r,θ,φ)=∂U∂rer→+1r∂U∂θeθ→+1rsin⁡θ∂U∂φeφ→.{\displaystyle \operatorname {grad} \,U(r,\;\theta ,\;\varphi )={\frac {\partial U}{\partial r}}{\vec {e_{r}}}+{\frac {1}{r}}{\frac {\partial U}{\partial \theta }}{\vec {e_{\theta }}}+{\frac {1}{r\sin {\theta }}}{\frac {\partial U}{\partial \varphi }}{\vec {e_{\varphi }}}.}

Медицина

В медицине существует несколько терминов, связанным со словом «градиент», таких как:

Градиент температурный. Он характеризует разницу в аналогичных показателях внутренних систем и кожных покровов тела.
Градиент физиологический. Он обозначает те или иные изменения в какой-либо системе органов или же организме в целом.
Градиент метаболический. Под ним подразумевается интенсивность обменных процессов.
Градиент давления. Он используется для обозначения разницы артериального давления в двух связанных друг с другом частях сердца.
Убывающий градиент автоматии. Это понятие характеризует автоматическое снижение частотности возбуждения сердечной мышцы.
Амплитуда градиента пульса. Данный показатель применяется для обозначения поражения сосуда и определения его степени посредством анализа разницы амплитуд систолических волн на кардиограмме.

Таким образом, понятие градиента в медицине может иметь массу разнообразных отличающихся друг от друга значений.

Медицинские показатели

Определение «градиент температурный» можно встретить также среди медицинских терминов. Он показывает разницу в соответствующих показателях внутренних органов и поверхности тела. В биологии градиент физиологический фиксирует изменение в физиологии любого органа или организма в целом на любой стадии его развития. В медицине показатель метаболический – интенсивность обмена веществ.

Не только физики, но и медики используют этот термин в работе. Что такое градиент давления в кардиологии? Такое понятие определяет разность кровяного давления в любых связанных между собой отделах сердечно-сосудистой системы.

Убывающий градиент автоматии – это показатель уменьшения частоты возбуждений сердца в направлении от его основания к верху, возникающие автоматически. Кроме того, кардиологи место поражения артерии и его степень выявляют благодаря контролю над разностью амплитуд систолических волн. Иными словами, с помощью амплитудного градиента пульса.

Производная по направлению и градиент функции трёх переменных

Грубо говоря, добавляется одно измерение и одно слагаемое. Рассмотрим функцию трёх переменных и точку , принадлежащую её области определения.

Если в точке существует производная по направлению пространственного луча (исходящего из точки ), то её можно рассчитать по следующей формуле:

, где:

– частные производные функции трёх переменных в точке ; – направляющие косинусы данного направления (они же соответствующие координаты направляющего вектора единичной длины).

Градиентом функции в точке называется направленный отрезок , отложенный от точки , который указывает направление наибыстрейшего возрастания данной функции в данной точке.

И обещанный физический пример: рассмотрим функцию трёх переменных , которая характеризует температуру некоего пространственного тела в каждой его точке . Тогда производная по тому или иному направлению в некоторой точке тела будет показывать скорость нагревания/охлаждения тела в соответствующих направлениях, а вектор – указывать направление наибыстрейшего роста температуры в этой точке.

Вот такой вот удачный и понятный пример – не какие-нибудь плохо представляемые электрические поля.

Закрепим формулы несколькими задачами:

Пример 8

Найти производную функции в точке по направлению вектора

Не тушуемся, это пространственный вектор:

Алгоритм решения остаётся прежним. Вычислим частные производные 1-го порядка в точке . Вот уж где точно нужен глаз да глаз: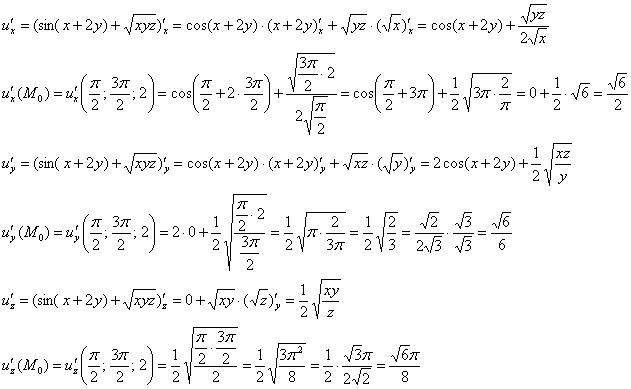
Найдем направляющие косинусы данного направления:

Контроль:

И завершающий шаг: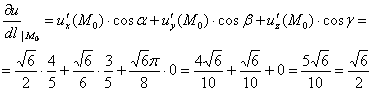

Ответ:

Пара символических заданий для самостоятельного решения:

Пример 9

Найти производную функции в точке по направлению, составляющему с положительными координатными полуосями равные углы.

Пример 10

Найти направление и величину наибыстрейшего возрастания функции в точке .

Особых комментариев я не оставлял, поскольку всё очень похоже на примеры 1-й части урока.

Аналогичным образом производная по направлению и градиент определяются и для функций бОльшего количества переменных.

Всех поздравляю! – сегодня мы не только познакомились с новым материалом, но и обобщили понятие производной, после чего ~~забудем о ней, как о кошмарном сне~~ можно смело приступать к изучению интегралов, разновидностей коих – великое множество…
…чувствую-чувствую, что взгрустнулось – вот и решил приободрить =)

Желаю вам выбора удачных направлений, которые, кстати, далеко не во всех точках жизни направлены по градиенту.

Спасибо за внимание и до скорых встреч!

Решения и ответы:

Пример 4: Решение: вычислим частные производные 1-го порядка в точке :Найдём направляющие косинусы:Искомая производная по направлению: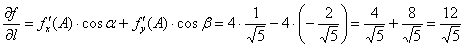Найдём градиент функции в точке и вычислим его длину:Таким образом, максимальная крутизна поверхности в точке :Ответ

Пример 5: Решение: вычислим частные производные 1-го порядка в точке :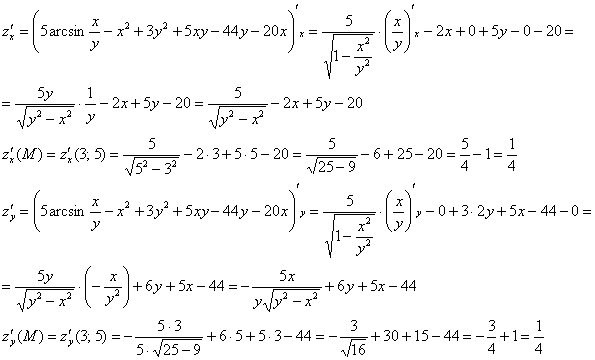Составим градиент функции в точке и вычислим его длину: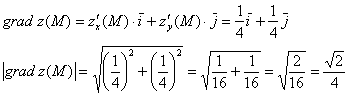Искомая производная по направлению: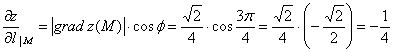Ответ

Пример 7: Решение: вычислим частные производные 1-го порядка в точке :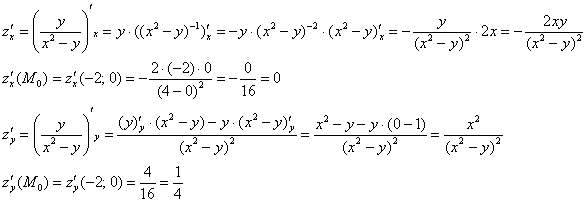

а) Вычислим производную по направлению , составляющему угол с положительным направлением оси . Рассмотрим единичный вектор , определяющий это направление. Очевидно, что . Таким образом:Искомая производная по направлению:

б) Рассмотрим единичный вектор , определяющий направление биссектрисы 4-го координатного угла. Очевидно, что его углы с положительными полуосями и соответственно равны (можно взять – ориентация угла не имеет значения) и . Таким образом:В результате производная по данному направлению:

Ответ

Пример 9: Решение: вычислим частные производные 1-го порядка в точке :Найдём направляющие косинусы предложенного направления. Используем равенство:Так как , то:И поскольку луч расположен в 1-м октанте:Искомая производная по направлению: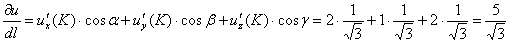Ответ

Пример 10: Решение: вычислим частные производные 1-го порядка в точке :Направление наибыстрейшего роста функции в точке задаёт вектор градиента в данной точке:Вычислим величину наибыстрейшего роста функции:Ответ

(Переход на главную страницу)

Рукоделие

Рукодельницам понятие «градиент» знакомо еще с одной стороны. Техника подобного плана используется в создании вещей ручной работы в стиле декупаж. Таким способом создают новые вещи под старину, или реставрируют старые: комоды, стулья, сундуки и прочее. Декупаж подразумевает нанесение узора с помощью трафарета, основой для которого служит градиент цвета, как фон.

Художники по тканям взяли на вооружение окраску таким способом для новых моделей. Платья с расцветкой градиент покорили подиумы. Моду подхватили рукодельницы – вязальщицы. Трикотажные вещи с плавным переходом цвета пользуются успехом.

Подводя итог определению «градиент», можно сказать об очень обширной области человеческой деятельности, в которой находится место этому термину. Не всегда замена синонимом «вектор» оказывается подходящей, так как вектор – это все-таки понятие функциональное, пространственное. В чем определяется общность понятия – это постепенное изменение определенной величины, субстанции, физического параметра на единицу за определенный период. В цвете – это плавный переход тона.

Термины метеорологов и географов

Впервые понятие градиента было применено именно метеорологами для определения изменения величины и направления различных метеорологических показателей: температуры, давления, скорости и силы ветра. Он является мерой количественного изменения различных величин. В математику термин ввел Максвелл уже значительно позднее. В определении погодных условий существуют понятия вертикального и горизонтального градиентов. Рассмотрим их подробнее.

Что такое градиент температуры вертикальный? Это величина, которая показывает изменение показателей, вычисленное на высот в 100 м. Может быть как положительного направления, так и отрицательного, в отличие от горизонтального, который всегда положителен.

Градиент показывает на местности величину или угол уклона. Вычисляется как отношение высоты к длине проекции пути на определенном участке. Выражается в процентах.

4) Градиент

Понятие градиента можно сформулировать по-разному. Начнём с локального определения, а именно, с градиента функции в отдельно взятой точке:

Градиентом функции в точке называется направленный отрезок , отложенный от точки , который показывает направление и скорость наискорейшего роста функции в данной точке.

Если совсем просто, то куда «смотрит» градиент – там и самый крутой «подъём в гору»

Распространённые обозначения: либо , причём здесь уже нельзя записывать просто (точнее, эта запись приобретает несколько другой смысл).

В нашем случае: .

И теперь заостряю внимание: градиент в точке – это вектор несвободный. По той причине, что характеризует поведение функции именно в данной точке, а не где-то ещё

Поэтому, следует отложить от начала координат. Однако он тоже оказывается под плоскостью , и «красный» вектор на чертеже, которым я обозначил общее направление – это на самом деле градиент в другой точке:

Взаимосвязь производной по направлению с градиентом:

Производная по некоторому направлению в точке – это проекция градиента в данной точке на данное направление:, откуда, согласно известным геометрическим выкладкам (см. ссылку выше), получается весьма полезная практическая формула:

, где:

– длина градиента; – угол между градиентом и данным направлением.

В свою очередь из этой формулы следует, что производная по направлению достигает максимального значения при , то есть когда – направление совпадает с направлением градиента.

В нашей задаче производная по направлению градиента: и максимальный «красный» угол подъёма:

Что такое градиент в физике?

Понятие градиента распространено во многих отраслях физики: градиент оптики, температуры, скорости, давления и т. д. В этой отрасли понятие обозначает меру возрастания или убывание величины на единицу. Вычисляется расчетами как разница между двумя показателями. Рассмотрим некоторые из величин подробнее.

Что такое градиент потенциала? В работе с электростатическим полем определяются две характеристики: напряженность (силовая) и потенциал (энергетическая). Эти разные величины связаны со средой. И хотя они и определяют разные характеристики, все же имеют связь между собой.

Для определения напряженности силового поля используется градиент потенциала – величина, которая определяет быстроту изменения потенциала по направлению силовой линии. Как рассчитать? Разность потенциалов двух точек электрического поля вычисляется по известному напряжению с помощью вектора напряженности, который равен градиенту потенциала.

Линейный градиент

Линейный градиент распространяется по прямой линии, демонстрируя плавный переход от одного оттенка цвета к другому. Линейный градиент создаётся с помощью функции linear-gradient(). Функция создаёт изображение, которое представляет собой линейный градиент между указанными оттенками цветов. Размер градиента соответствует размеру элемента, к которому он применён.

Функция linear-gradient() принимает следующие, разделяемые запятой, аргументы:

В качестве первого аргумента указывается градус угла или ключевые слова, определяющие угол направления линии градиента. Необязательный аргумент.
Разделяемый запятыми список состоящий из двух или более цветов, за каждым из которых может следовать стоп позиция.

Простейший линейный градиент требует только два аргумента, определяющие начальный и конечный цвет:

div {
  background-image: linear-gradient(black, white);
  width: 200px;
  height: 200px;
}

Попробовать »

При передаче функции двух аргументов устанавливается вертикальный градиент с начальной точкой сверху.

Направление линии градиента может быть определено двумя способами:

Использование градусов: В качестве первого аргумента можно передать градус угла линии градиента, определяющий направление градиента, так например, угол 0deg (deg сокращение от англ degree — градус) определяет линию градиента от нижней границы элемента к верхней, угол 90deg определяет линию градиента слева на право и т.д. Проще говоря, положительные углы представляют собой вращение по часовой стрелке, отрицательные соответственно против часов.
Использование ключевых слов: В качестве первого аргумента могут также передаваться ключевые слова «to top», «to right», «to bottom» или «to left», они представляют собой углы линий градиентов «0deg» «90deg» «180deg» «270deg» соответственно.
Угол можно так же задать с помощью двух ключевых слов, например, to top right — линия градиента направлена в верхний правый угол.

Пример градиента заданного в разных направлениях:

div { 
  margin: 10px;
  width: 200px;
  height: 200px;
  float: left;
}
#one { background-image: linear-gradient(to left, black, red); }
#two { background-image: linear-gradient(to top left, black, red); }
#three { background-image: linear-gradient(65deg, black, yellow); }

Попробовать »

Как уже упоминалось, линейный градиент может включать список более чем из двух цветов, разделяемых запятой, браузер будет их равномерно распределять по всей доступной области:

div { 
  margin: 10px;
  width: 200px;
  height: 200px;
  float: left;
}
#one { background-image: linear-gradient(to right, red, blue, yellow); }
#two { background-image: linear-gradient(to top left, blue, white, blue); }

Попробовать »

После цвета допускается указывать стоп позицию для него, которая определяет место расположение цвета (где один цвет начинает переходить в другой) относительно начальной и конечной точки градиента. Стоп позиция указывается с помощью единиц измерения поддерживаемых в CSS или с помощью процентов. При использовании процентов, расположение стоп позиции вычисляется в зависимости от длины линии градиента. Значение 0% является начальной точкой градиента, 100% — конечной.

div { 
  margin: 10px;
  width: 200px;
  height: 200px;
  float: left;
}
#one { background-image: linear-gradient(to top right, blue, white 70%, blue); }
#two { background-image: linear-gradient(to right bottom, yellow 10%, white, red, black 90%);}
#three { background-image: linear-gradient(to right, black 10%, yellow, black 90%); }

Попробовать »

Значение цвета можно указывать различными способами, например: указать имя цвета, использовать (HEX), с помощью синтаксиса (RGBA) или (HSLA). Например, использование градиента с прозрачностью может быть использовано в сочетании с фоновым цветом или изображением, расположенным под градиентом для создания интересных визуальных эффектов:

div { 
  margin: 10px;
  width: 300px;
  height: 100px;
  background-color: green;
}
#one { background: linear-gradient(to left, rgb(255,255,0), rgba(255,255,0,0)); }
#two { background: linear-gradient(rgb(255,255,255), rgba(255,255,255,0)); }

Попробовать »

Математические функции

Что такое градиент функции в математике? Это вектор, направление которого указывает направление роста функции в скалярном поле от одного значения к другому. Величина градиента рассчитывается с помощью определения частных производных. Для выяснения максимально быстрого направления роста функции на графике выбираются две точки. Они определяют начало и конец вектора. Скорость роста значения от одной точки к другой – это величина градиента. Математические функции, основанные на расчетах этого показателя, используются в векторной компьютерной графике, объектами которой являются графические изображения математических объектов.

Что говорят словари?

Что такое «градиент» специальные тематические словари трактуют в соотношении со своей спецификой. В переводе с латинского языка это слово обозначает — «тот, который идет, растет». А «Википедия» определяет это понятие как «вектор, указывающий направление возрастания величины». В толковых словарях мы видим значение этого слова как «изменение любой величины на одно значение». Понятие может нести как количественное, так и качественное значение.

Если коротко, то это плавный постепенный переход любой величины на одно значение, прогрессивное и непрерывное изменение в количестве или направлении. Вектор вычисляют математики, метеорологи. Это понятие применяют в астрономии, медицине, искусстве, компьютерной графике. Под схожим термином определяются совершенно не схожие виды деятельности.

Градиент цвета

Термин «градиент» знаком творческим личностям. Хоть они и далеки от точных наук. Что такое градиент для художника, декоратора, дизайнера? Так как в точных науках – это постепенное увеличение величины на единицу, так и в цвете этот показатель обозначает плавный, растянутый переход оттенков одного цвета от более светлого к темному, или же наоборот. Художники так и называют этот процесс – «растяжка». Возможен переход и к разным сопутствующим цветам в одной гамме.

Градиентные растяжки оттенков в окраске помещений заняли прочную позицию среди методик дизайна. Новомодный стиль омбре — плавное перетекание оттенка от светлого к темному, от яркого к бледному — эффектно преобразует любое помещения в доме и в офисе.

Оптики используют специальные линзы в солнцезащитных очках. Что такое градиент в очках? Это изготовление линзы особым способом, когда сверху вниз цвет переходит от более темного к более светлому оттенку. Изделия, изготовленные по такой технологии, защищают глаза от солнечного излучения и позволяют рассматривать предметы даже при очень ярком свете.

Определение

Для случая трёхмерного пространства градиентом
скалярной функции φ=φ(x,y,z){\displaystyle \varphi =\varphi (x,y,z)} координат x{\displaystyle x}, y{\displaystyle y}, z{\displaystyle z} называется векторная функция с компонентами

∂φ∂x,∂φ∂y,∂φ∂z.{\displaystyle {\frac {\partial \varphi }{\partial x}},{\frac {\partial \varphi }{\partial y}},{\frac {\partial \varphi }{\partial z}}.}

Или, использовав для единичных векторов по осям прямоугольных декартовых координат e→x,e→y,e→z{\displaystyle {\vec {e}}_{x},{\vec {e}}_{y},{\vec {e}}_{z}}:

gradφ=∇φ=∂φ∂xe→x+∂φ∂ye→y+∂φ∂ze→z.{\displaystyle \mathrm {grad} \,\varphi =\nabla \varphi ={\frac {\partial \varphi }{\partial x}}{\vec {e}}_{x}+{\frac {\partial \varphi }{\partial y}}{\vec {e}}_{y}+{\frac {\partial \varphi }{\partial z}}{\vec {e}}_{z}.}

Если φ{\displaystyle \varphi } — функция n{\displaystyle n} переменных x1,…,xn{\displaystyle x_{1},\;\ldots ,\;x_{n}}, то её градиентом называется n{\displaystyle n}-мерный вектор

(∂φ∂x1,…,∂φ∂xn),{\displaystyle \left({\frac {\partial \varphi }{\partial x_{1}}},\;\ldots ,\;{\frac {\partial \varphi }{\partial x_{n}}}\right),}

компоненты которого равны частным производным φ{\displaystyle \varphi } по всем её аргументам.

Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идёт речь.
Оператором градиента называется оператор, действие которого на скалярную функцию (поле) даёт её градиент. Этот оператор иногда коротко называют просто «градиентом».

Смысл градиента любой скалярной функции f{\displaystyle f} в том, что его скалярное произведение с бесконечно малым вектором перемещения dx{\displaystyle d\mathbf {x} } даёт полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена f{\displaystyle f}, то есть линейную (в случае общего положения она же главная) часть изменения f{\displaystyle f} при смещении на dx{\displaystyle d\mathbf {x} }. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

df=∂f∂x1dx1+∂f∂x2dx2+∂f∂x3dx3+…=∑i∂f∂xidxi=(gradf⋅dx).{\displaystyle df={\frac {\partial f}{\partial x_{1}}}\,dx_{1}+{\frac {\partial f}{\partial x_{2}}}\,dx_{2}+{\frac {\partial f}{\partial x_{3}}}\,dx_{3}+\ldots =\sum _{i}{\frac {\partial f}{\partial x_{i}}}\,dx_{i}=(\mathrm {grad} \,\mathbf {f} \cdot d\mathbf {x} ).}

Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат xi{\displaystyle x_{i}}, то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку dx{\displaystyle d\mathbf {x} } — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

df=∑i(∂if)dxi{\displaystyle df=\sum _{i}(\partial _{i}f)\,dx^{i}}

или, опуская по правилу Эйнштейна знак суммы,

df=(∂if)dxi{\displaystyle df=(\partial _{i}f)\,dx^{i}}

(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше).
Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

Используя интегральную теорему

∭V∇φdV=∬Sφds{\displaystyle \iiint \limits _{V}\nabla \varphi \,dV=\iint \limits _{S}\varphi \,d\mathbf {s} },

градиент можно выразить в интегральной форме:

∇φ=limV→1V(∬Sφds),{\displaystyle \nabla \varphi =\lim \limits _{V\to 0}{\frac {1}{V}}\left(\iint \limits _{S}\varphi \,d\mathbf {s} \right),}

здесь S{\displaystyle {\it {S}}} — замкнутая поверхность охватывающая объём V,ds{\displaystyle {\it {{V},d\mathbf {s} }}} — нормальный элемент этой поверхности.