Параллакс

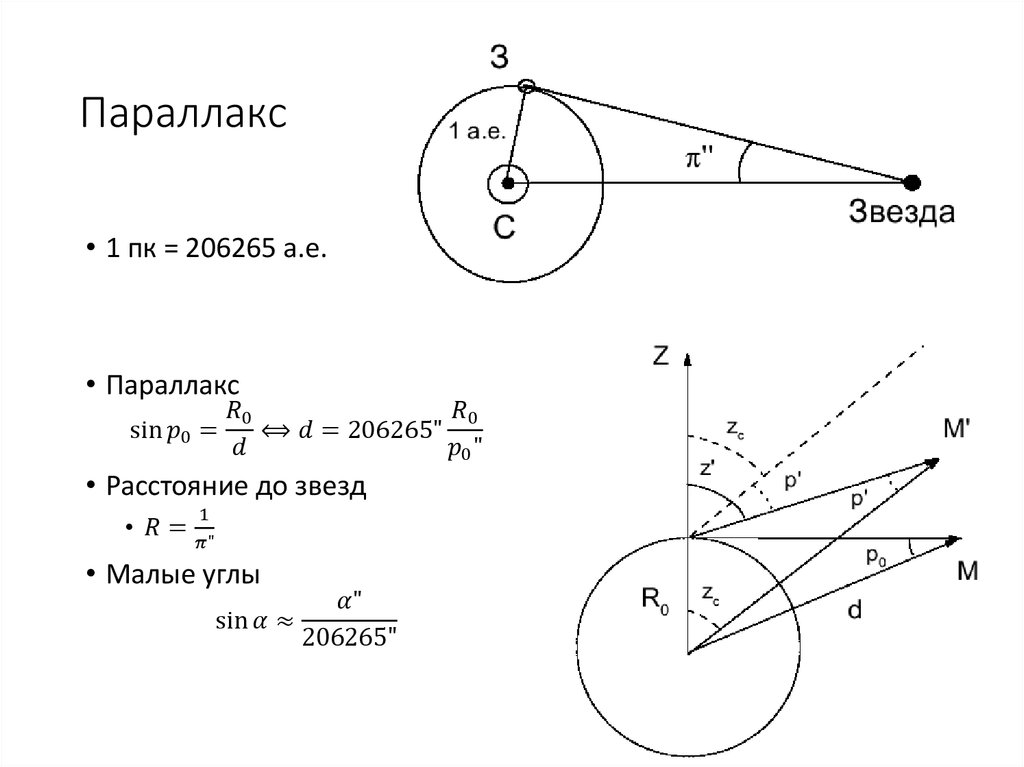
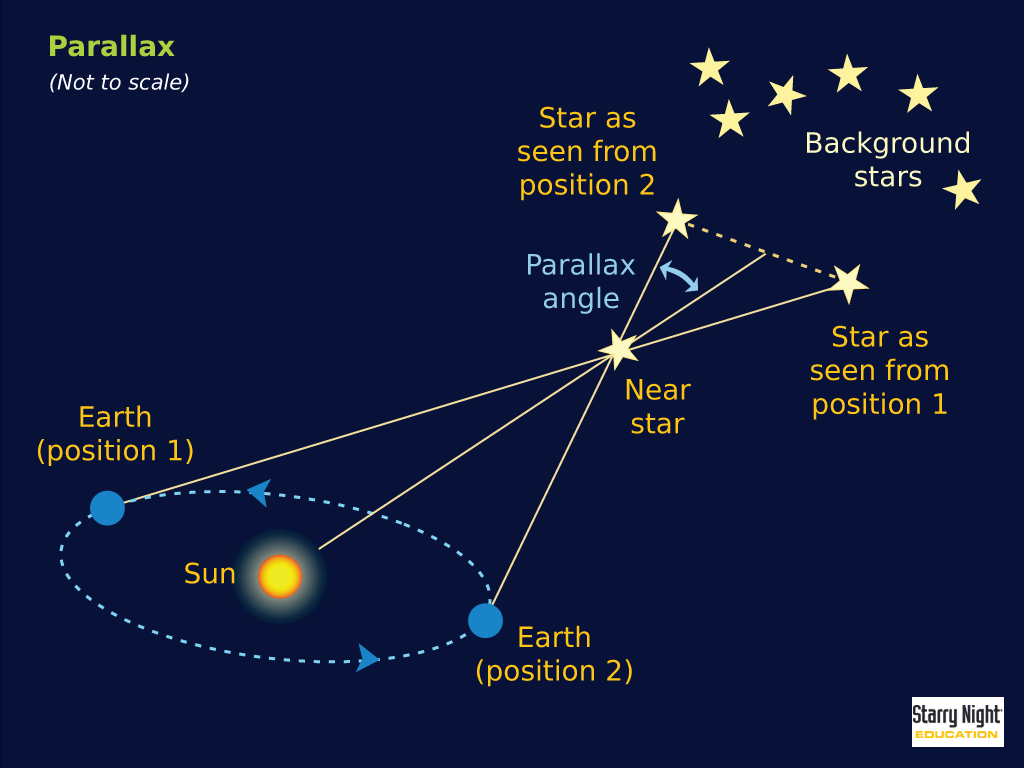
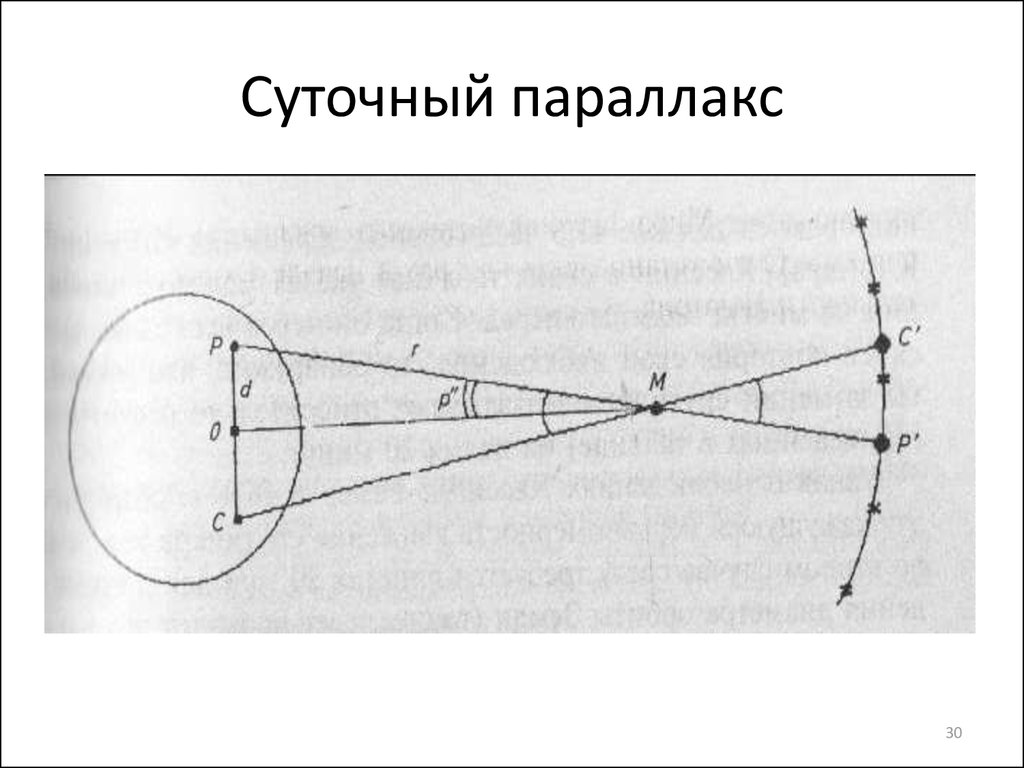
Параллакс.

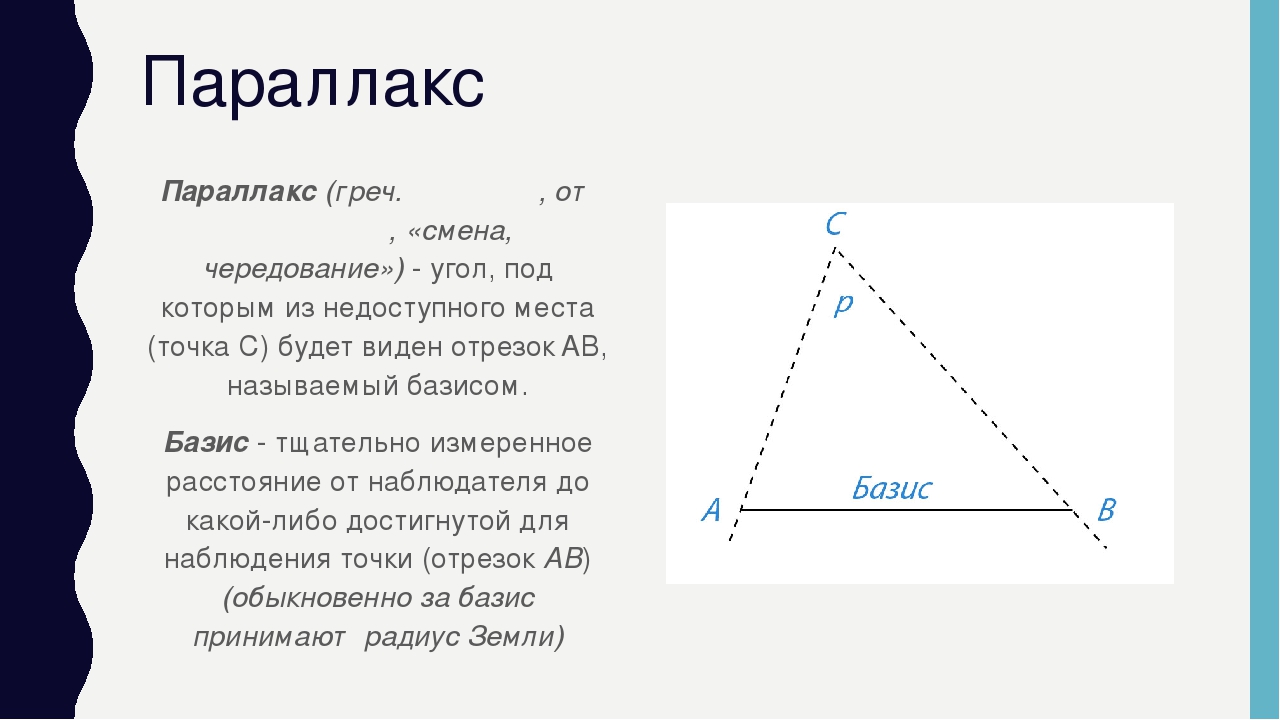
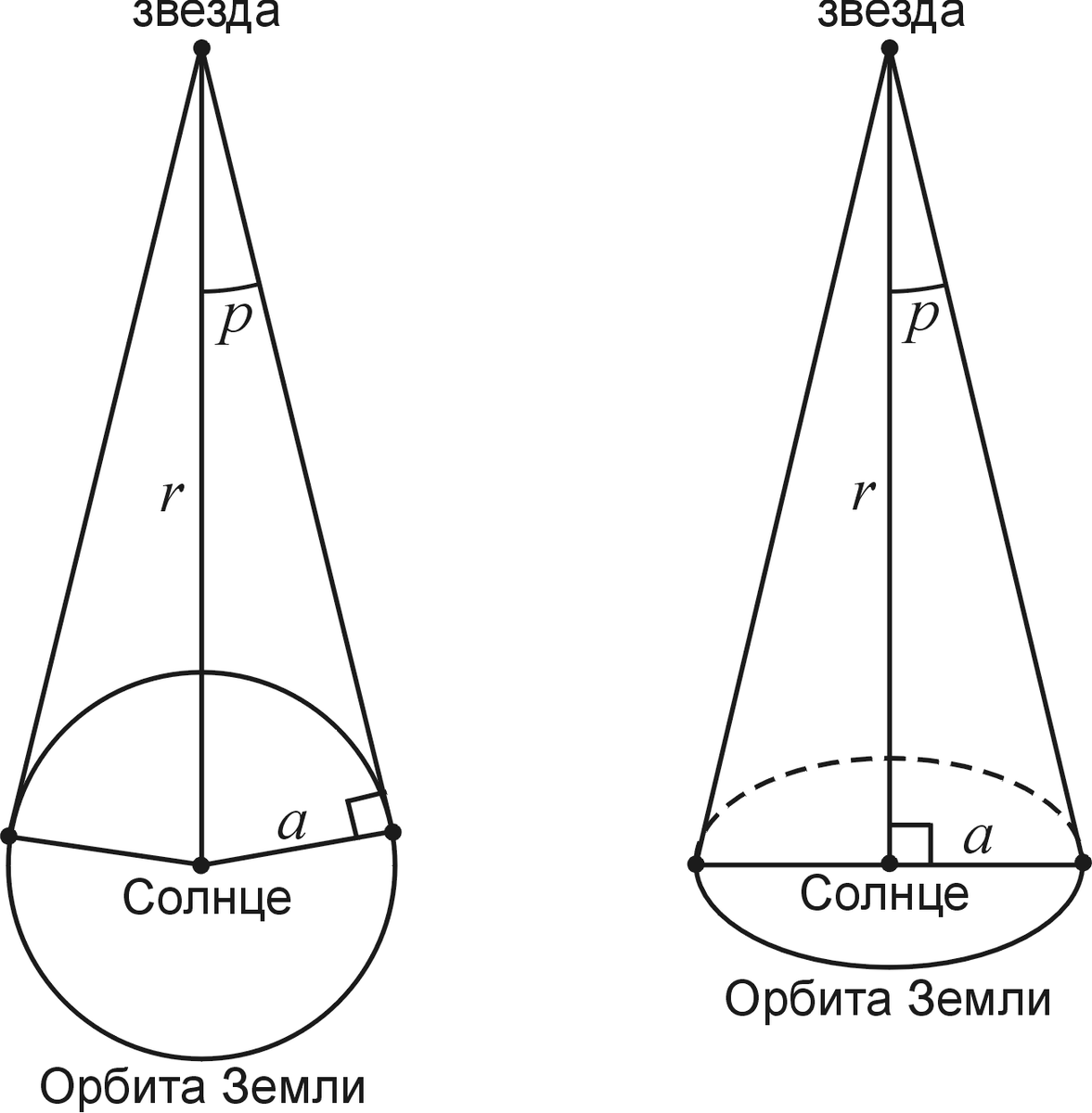
Явление параллакса.Параллакс (параллактическое смещение) — кажущееся смещение светила, обусловленное перемещением наблюдателя. Параллактические смещения светила тем больше, чем ближе светило к наблюдателю и чем больше перемещение наблюдателя.Топоцентрические координаты светил — координаты светил, определенные из точки на поверхности Земли. Топоцентрические координаты каждого светила в один и тот же момент различны для различных точек поверхности Земли. Это различие заметно для тел Солнечной системы и практически не ощутимо для звезд.Суточный параллакс светила.Суточный параллакс светила — разность направлений, по которым светило было бы видно из центра Земли и из какой-нибудь точки ее поверхности. Можно сказать, что суточный параллакс — есть угол р’, под которым со светила был бы виден радиус Земли в месте наблюдения. Для светила, находящегося в зените места наблюдения, суточный параллакс равен 0. Суточный горизонтальный параллакс р — максимальное значение, которое может принимать суточный параллакс. Это происходит, когда светило находится на горизонте. Суточный параллакс и суточный горизонтальный параллакс связаны соотношениемp’ = p sin z,
где z — зенитное расстояние светила.
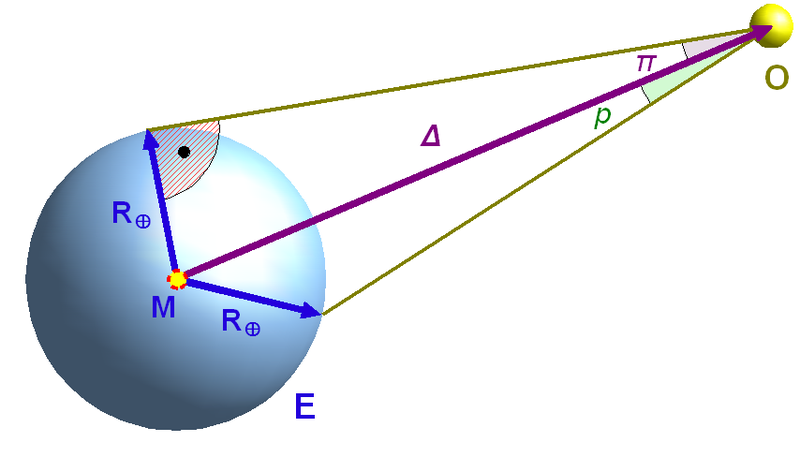
Суточный горизонтальный параллакс.Горизонтальный экваториальный параллакс. Определение расстояния от центра Земли до светила.Горизонтальный экваториальный параллакс р — суточный горизонтальный параллакс светила для точек, лежащих на экваторе. Горизонтальный экваториальный параллакс связан с суточным горизонтальным параллаксом соотношениемр = р x а/ρ,
где а — экваториальный радиус Земли, ρ — радиус Земли в месте наблюдения.
Для большинства тел Солнечной системы горизонтальный экваториальный параллакс меньше 30″ и только для Луны он может достигать 62′.
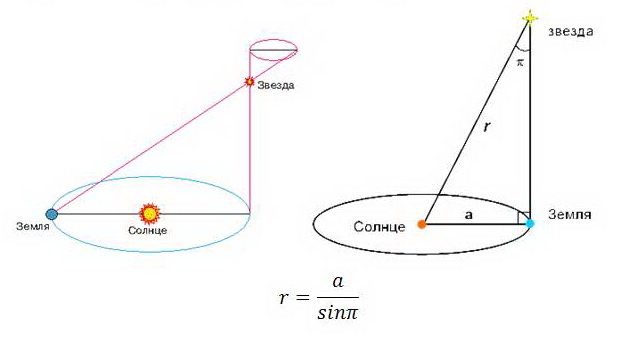
Знание горизонтального экваториального параллакса позволяет легко определить расстояние Δ от центра Земли до светила по формулеΔ = а/sin р.
Если принять горизонтальный экваториальный параллакс Солнца равным 8″,794, то расстояние Солнца от Земли будет равно 149 600 000 км. Это расстояние в астрономии называется астрономической единицей (а.е.).
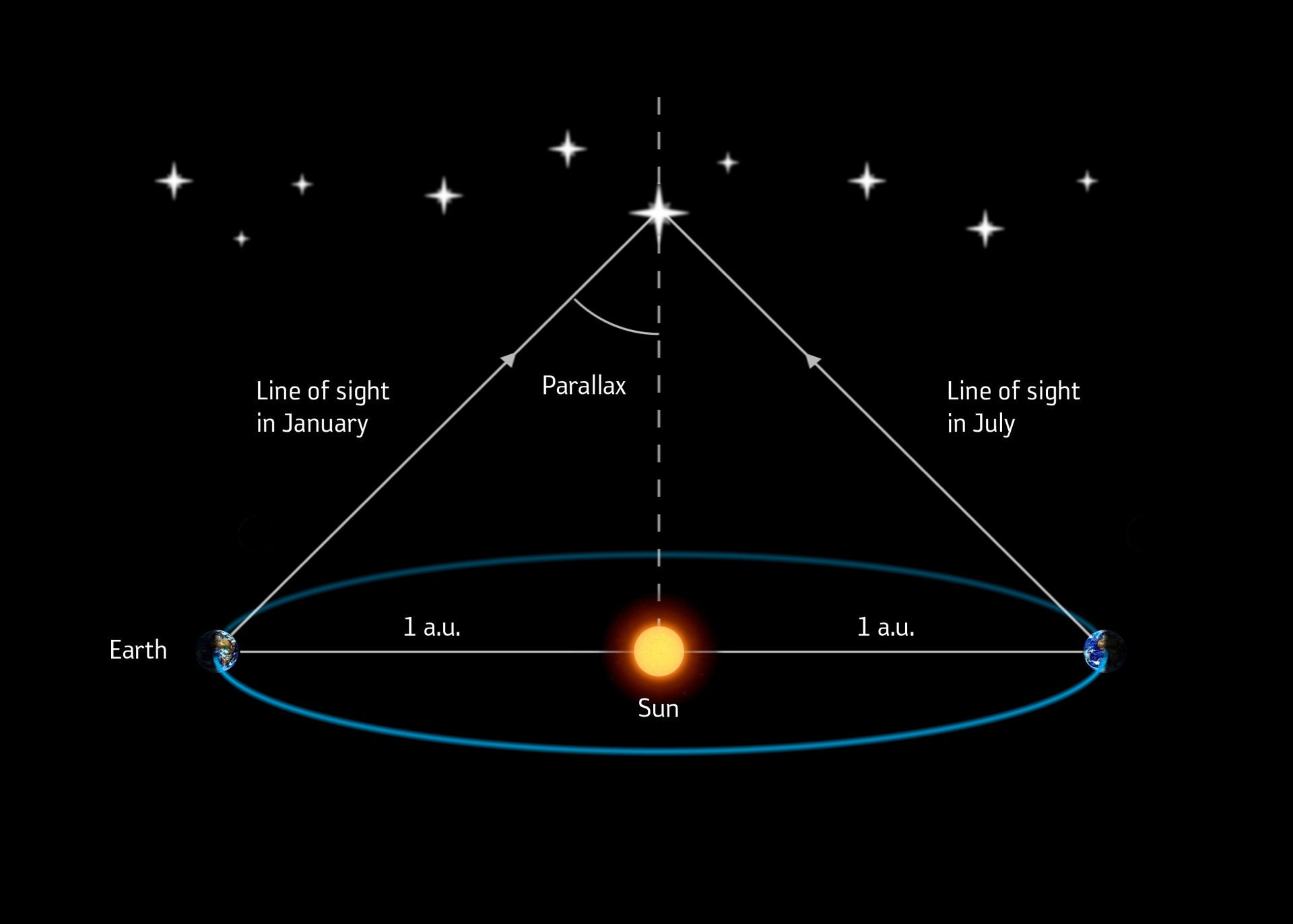
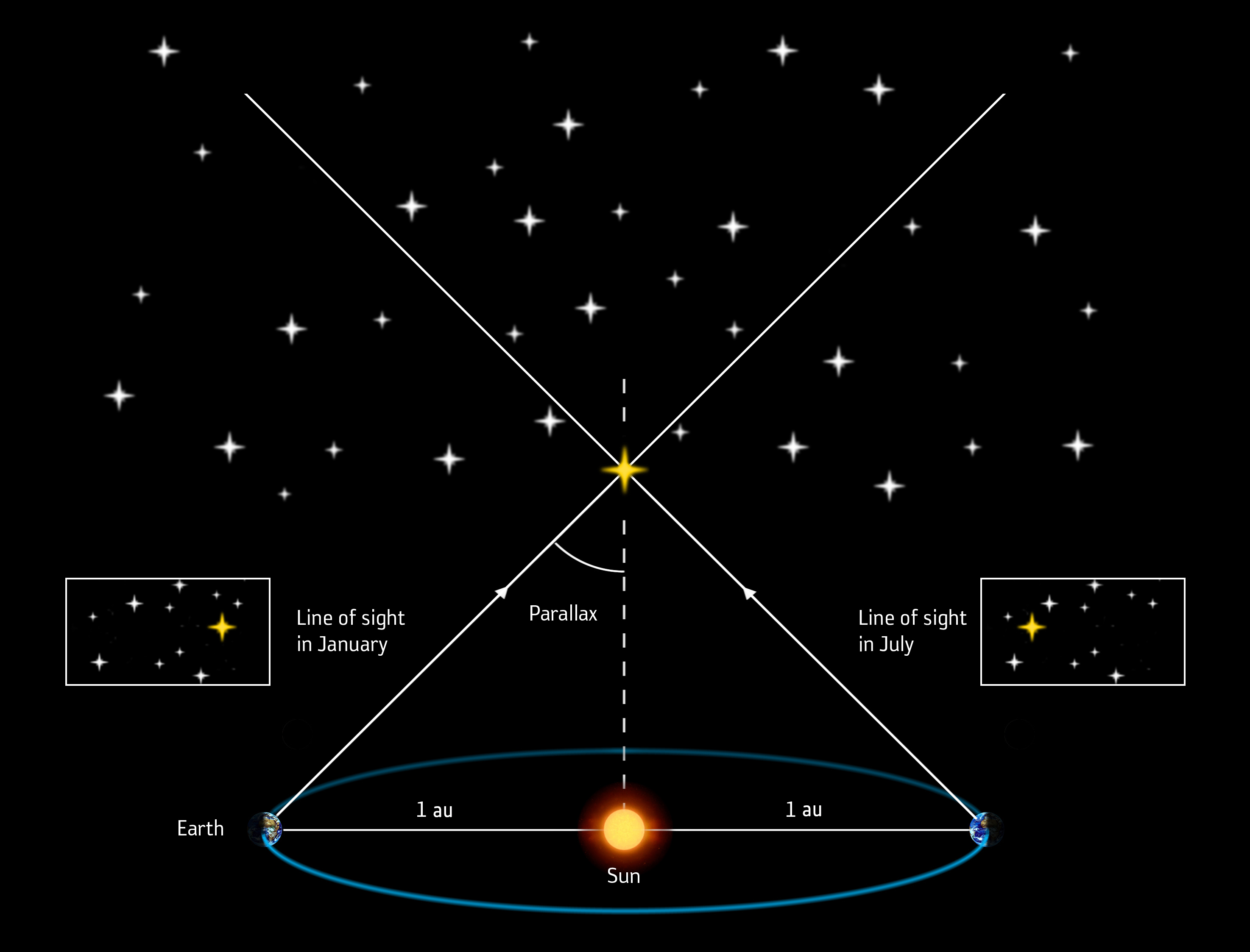
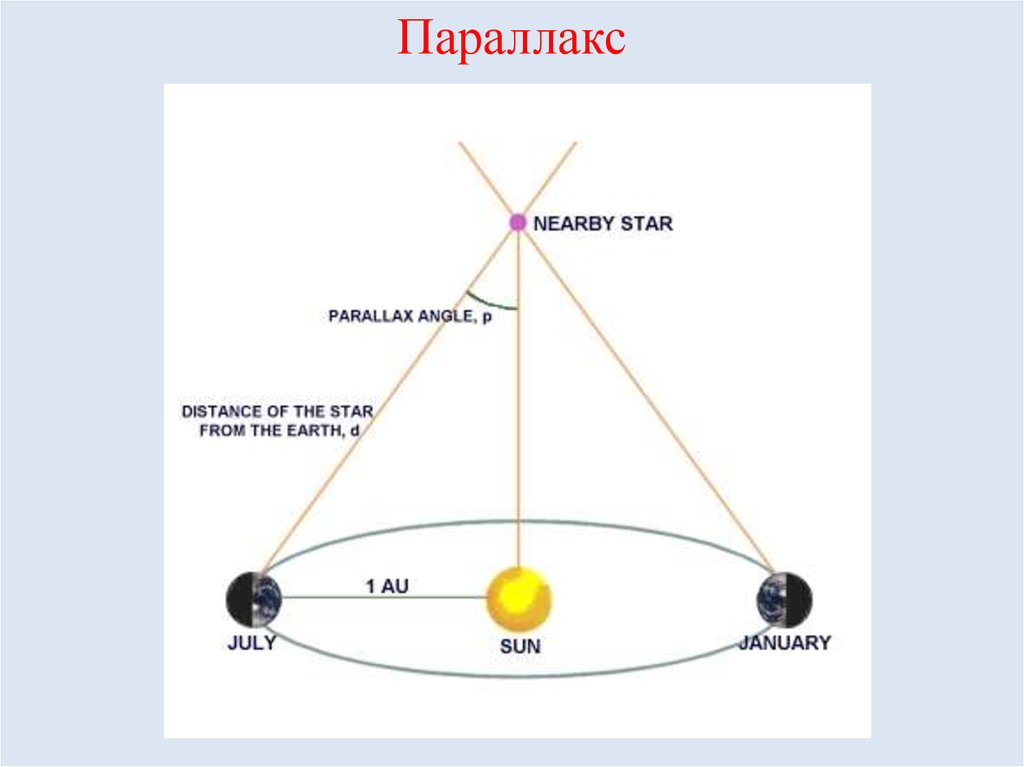
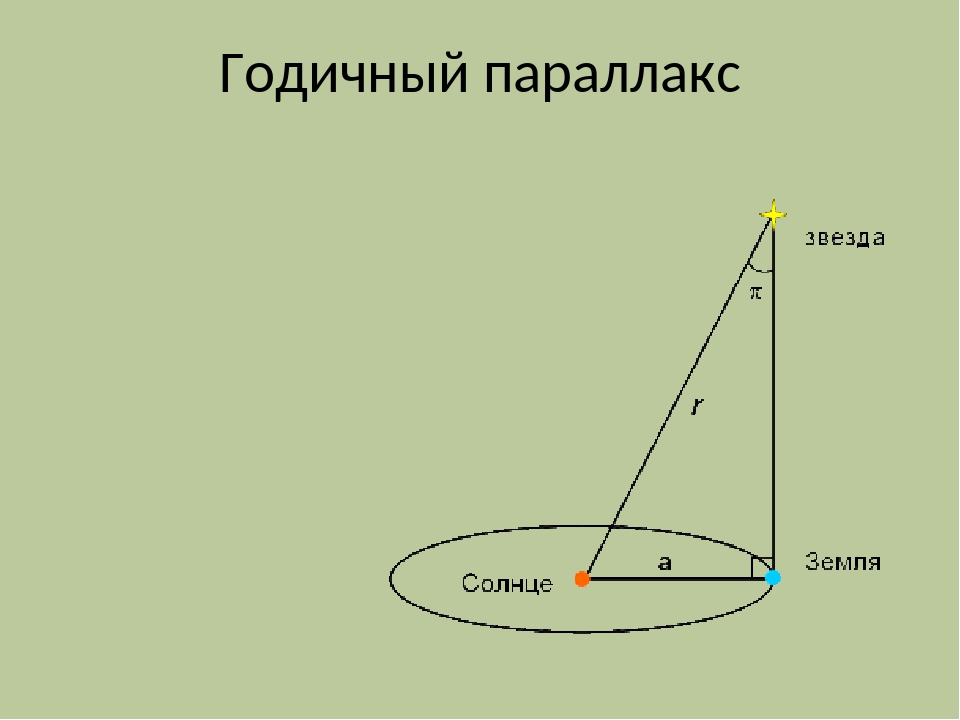
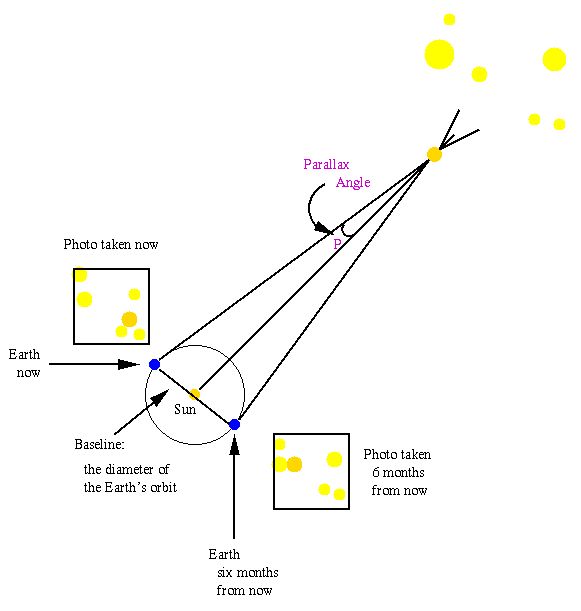
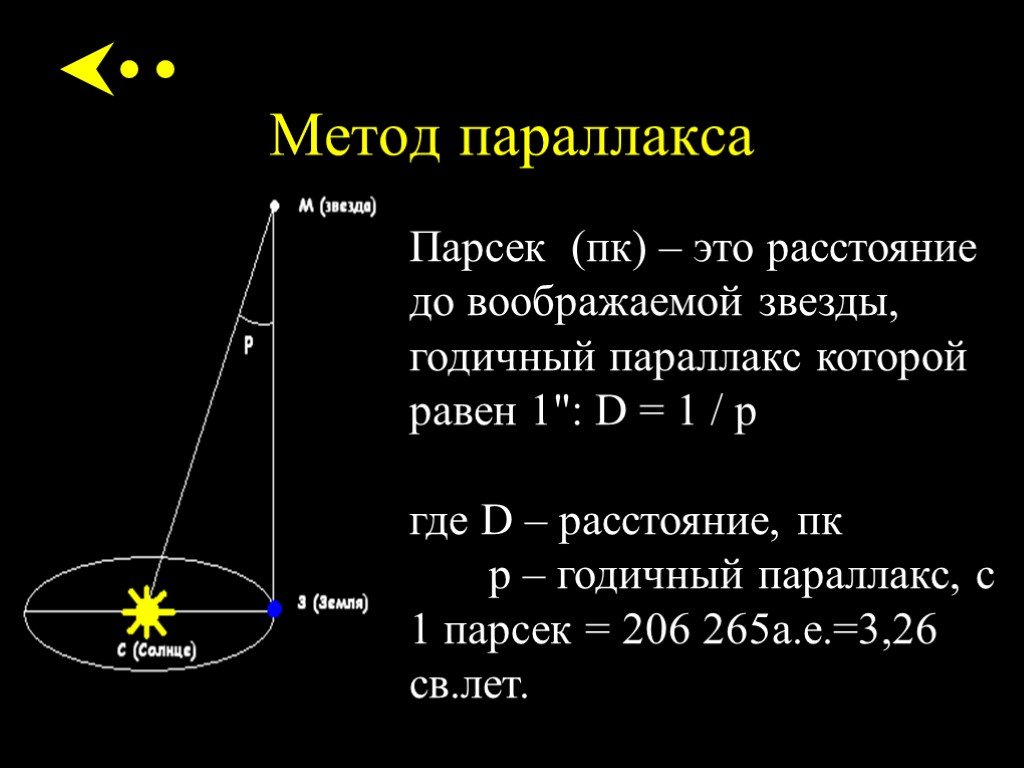
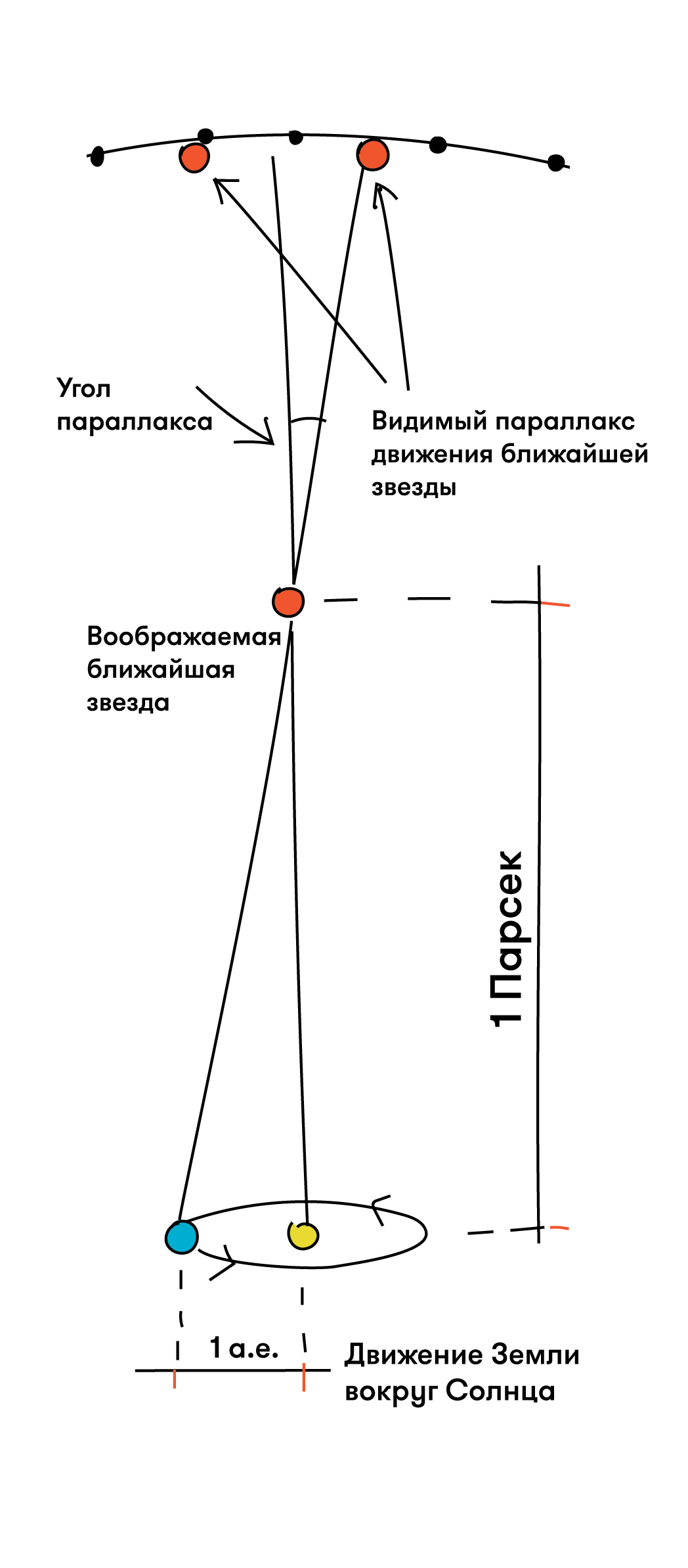
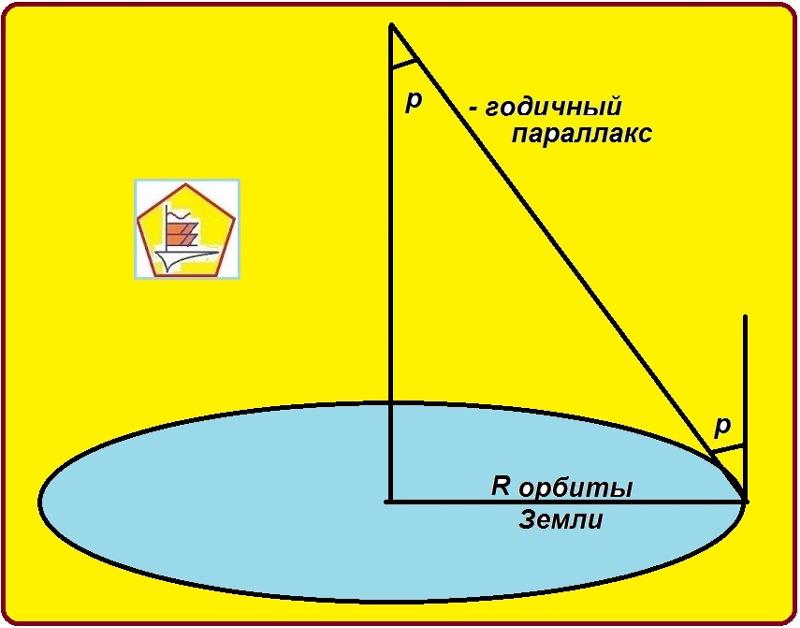
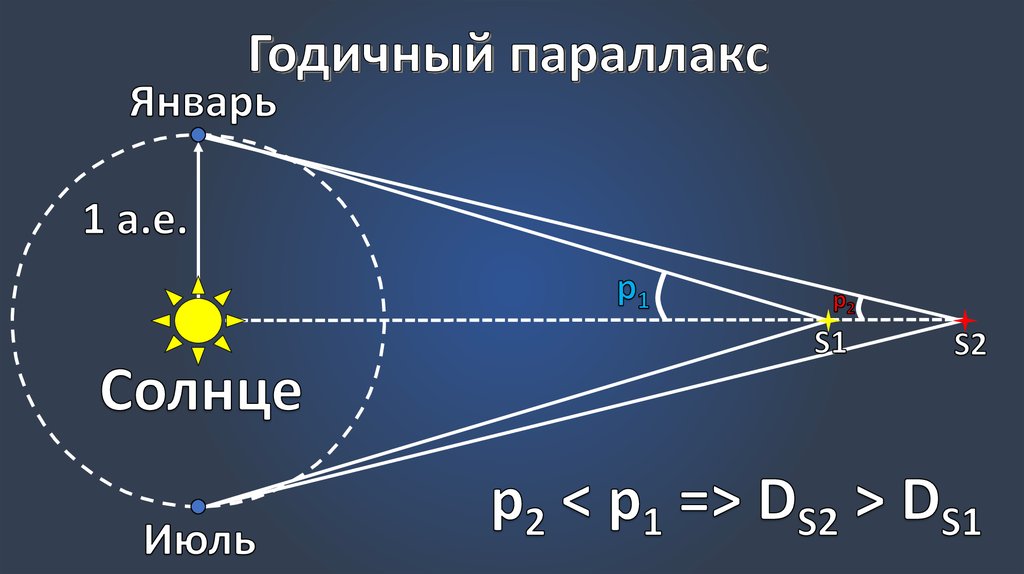
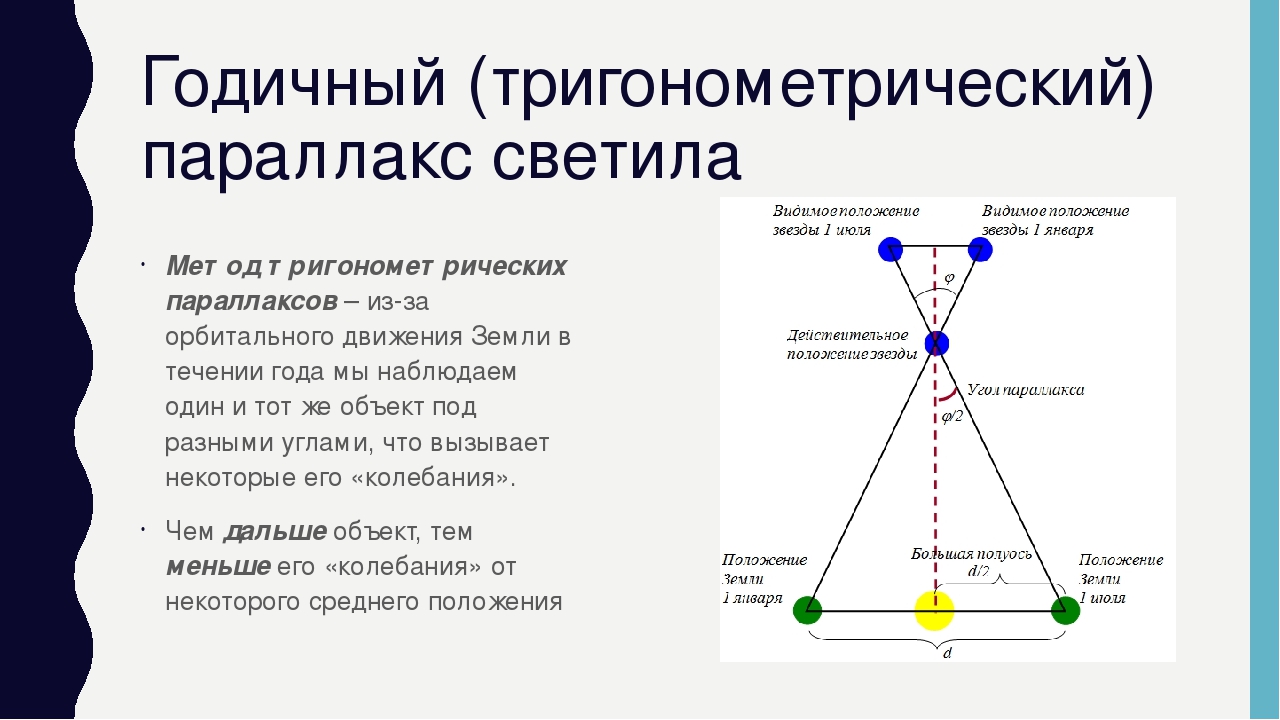
Горизонтальный экваториальный параллакс.Годичный параллакс звезды. Определение расстояния от Солнца до звезды.Годичный параллакс звезды π — угол под которым со звезды был бы виден средний радиус земной орбиты при условии, что направление на звезду перпендикулярно к радиусу. Так как величина годичных параллаксов звезд не превышает 1″, влияние годичного параллакса на координаты звезд учитывается только при высокоточных наблюдениях.

При помощи годичного параллакса можно определить расстояние D звезды от Солнца по формулеD = а.е./sin π.
Расстояние, соответствующее годичному параллаксу в 1″, называется парсеком (пс).
1 пс = 206 265 а.е. = 3,086 х 1013 км.
Расстояние, составляющее 1 000 парсек, называется килопарсеком, а расстояние в 1 000 000 парсек — мегапарсеком.Световой год — расстояние, которое свет проходит за один год со скоростью около 300 000 км/сек.
1 световой год = 9,46 х 1012 км = 63 240 а. е. = 0,3067 пс.
1 пс = 3,26 светового года.

Годичный параллакс звезд.

Краткие сведения

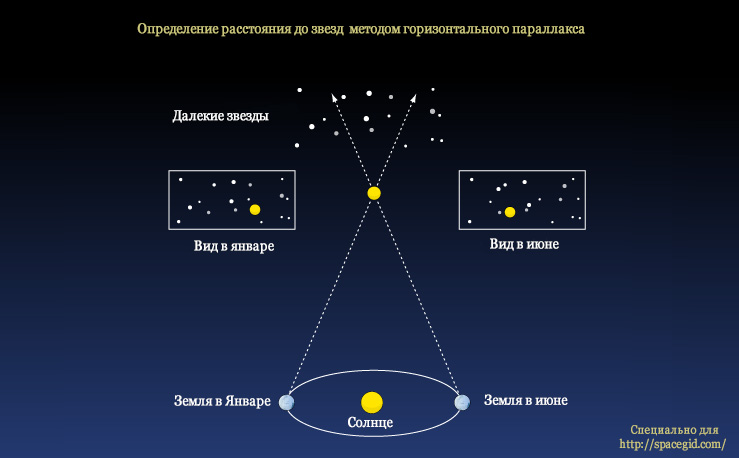
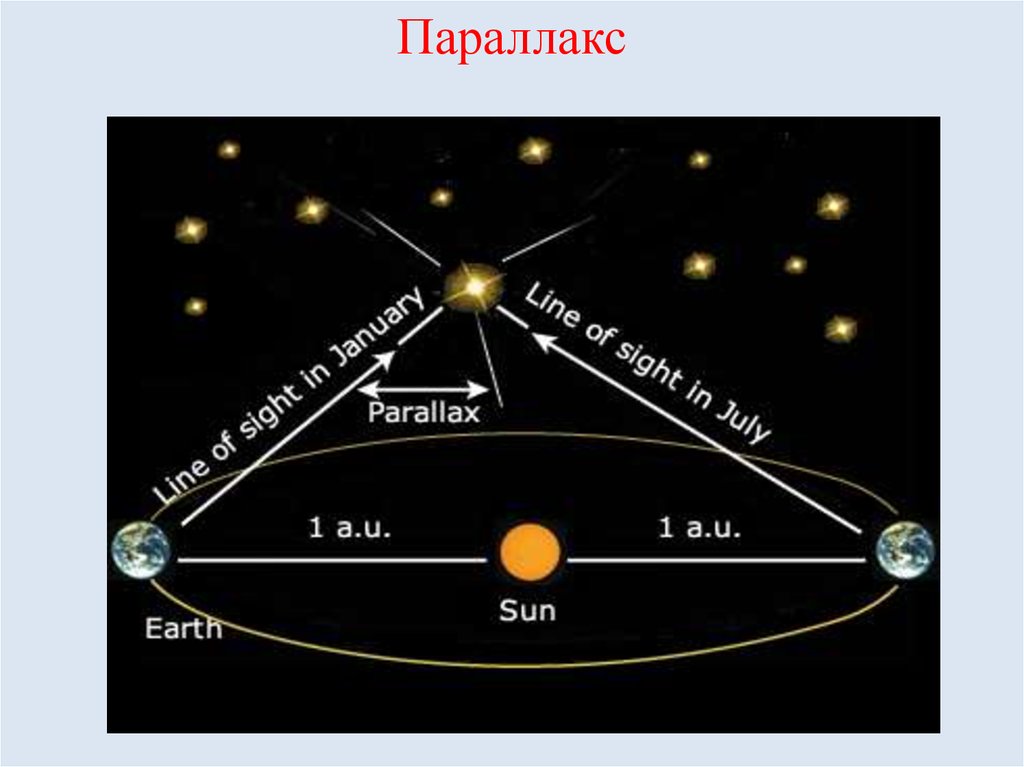
Радиус земной орбиты составляет одну астрономическую единицу или около 150 миллионов километров. В связи с этим все внеземные объекты на земном небе так же выписывают годичные “петли” (параллактическое движение). Чем дальше небесный объект находится от Земли, тем его параллактическое движение на земном небе является менее заметным (в переводе с греческого слово “параллакс” означает “смещение”).

Измерения углового диаметра параллактического движения небесных тел на земном небе позволяет проводить наиболее точные измерения расстояния до них (тригонометрическое расстояние). Кроме того, важным в истории астрономии оказался суточный (геоцентрический) и вековой параллакс. Первый из них обозначает половину от максимального различия в угловых координатах небесного тела на земном небе при различных географических положениях на поверхности Земли (относительно центра Земли), второй обозначает собственные движения звезд на небе нашей планеты по причине движения Солнечной Системы вокруг центра галактики.

Светимость

Светимость — название ряда физических величин .

В фотометрии светимость — это световая величина , представляющая собой световой поток излучения, испускаемого с малого участка светящейся поверхности единичной площади . Она равна отношению светового потока, исходящего от рассматриваемого малого участка поверхности, к площади этого участка:

где dΦv — световой поток, испускаемый участком поверхности площадью d S . Светимость в Международной системе единиц (СИ) измеряется в лм /м². 1 лм/м² — это светимость поверхности площадью 1 м2, излучающей световой поток, равный 1 лм.

Аналогом светимости в системе энергетических фотометрических величин является энергетическая светимость (излучательность). Её определение аналогично определению светимости, но вместо светового потока Φvиспользуется поток излучения Фe. Единица энергетической светимости в СИ — Вт /м².

Светимость в астрономии — полная энергия , излучаемая астрономическим объектом ( планетой , звездой , галактикой и т. п.) в единицу времени . Измеряется в абсолютных единицах ( СИ — Вт ; СГС — эрг /с) либо в единицах светимости Солнца ( L ☉ = 3,86⋅1033 эрг /с = 3,86⋅1026Вт).

Светимость астрономического объекта не зависит от расстояния до объекта, от него зависит только видимая звёздная величина . Светимость — одна из важнейших звёздных характеристик, позволяющая сравнивать между собой различные типы звёзд на диаграммах «спектр — светимость» , «масса — светимость». Светимость звезд главной последовательности можно приближенно рассчитать по формуле:

Светимость самых ярких звёзд в миллионы раз превышает светимость Солнца.

В экспериментальной физике элементарных частиц светимостью называют параметр ускорителя , характеризующий интенсивность столкновения частиц пучка с частицами фиксированной мишени (интенсивность столкновения частиц двух встречных пучков в случае коллайдеров ). Светимость L измеряется в см−2·с−1. При умножении сечения реакции на светимость получается средняя частота протекания этого процесса на данном коллайдере N˙process=L⋅σprocess{\displaystyle {\dot {N}}_{\text{process}}=L\cdot \sigma _{\text{process}}} .

Светимость Большого адронного коллайдера во время первых недель работы пробега была не более 1029частиц/см²·с, но она продолжает постоянно повышаться. Целью является достижение номинальной светимости в 1,7⋅1034частиц/см²·с, что по порядку величины соответствует светимостям BaBar ( SLAC , США) и Belle ( KEK , Япония ). Коллайдеру KEKB принадлежит мировой рекорд светимости для ускорителей с встречными пучками — 2,11⋅1034см−2·с−1.

Основы геометрии и тригонометрии

При вычислении лунного параллакса активно используются основы геометрии для прямоугольного треугольника. Прямоугольным треугольником называется такой треугольник, у которого один из углов равен 90 градусов.

В прямоугольном треугольнике стороны, которые образуют угол в 90 градусов, называются катетами, а сторона, лежащая напротив угла в 90 градусов гипотенузой. Сумма углов в прямоугольном треугольнике равна 180 градусов. Отсюда несложно определить, что при известном катете (радиусе Земли) и угле между гипотенузой и катетом (суточным параллаксом) гипотенуза (расстояние до небесного тела) будет равна отношению известного катета к синусу суточного параллакса.

Только в этом случае радиус Земли заменяется радиусом земной орбиты вокруг Солнца, а суточный параллакс заменяется годичным параллаксом

Синусом в прямоугольном треугольнике называют отношение катета противолежащего угла к гипотенузе.

Аналогичный принцип вычислений существует для расчетов тригонометрических расстояний до звезд.

По причине огромных расстояний до звезд (ближайшая звезда находится в 270 тысячах астрономических единиц от Солнца), для вычисления тригонометрических расстояний чаще всего используют отношение 206265 угловых секунд и измеренного годичного параллакса, который так же представлен в угловых секундах. Число 206265 означает число угловых секунд в одном радиане. Радиан – это угол, соответствующий дуге окружности, длина которой равна радиусу этой окружности.

Современное состояние вопроса

Макет космического аппарата Gaia на салоне Ле Бурже, 2013

В настоящее время наземные оптические измерения позволяют в некоторых случаях снизить ошибку в измерении параллакса до 0,005″, что соответствует предельному расстоянию в 200 пк. Дальнейшее повышение точности измерений стало возможным благодаря использованию космических телескопов. Специально для астрометрических целей Европейским космическим агентством (ЕКА) в 1989 году был запущен космический телескоп Hipparcos, позволивший измерить параллаксы более 100 тысяч звёзд с точностью до 0,001″. В 2013 году ЕКА запустило новый космический телескоп — Gaia. Планируемая точность измерения параллакса ярких звёзд (до 15 m) будет выше 25 миллионных долей секунды, для слабых звёзд (около 20 m) — до 300 миллионных долей секунды. Измерение годичных параллаксов позволяет производить также один из инструментов Космического телескопа им. Хаббла — Широкоугольная камера 3. Точность измерения параллаксов составляет от 20 до 40 миллионных долей секунды, что позволяет измерять расстояния до 5 килопарсек. В частности, был измерен параллакс переменной звезды SU Возничего.

Значительным достижением конца XX века явилось использование для параллактических измерений метода сверхдальной радиоинтерферометрии. Погрешность при этом может составлять до 10 миллионных долей угловой секунды. Этот метод применяется для измерения расстояния до компактных радиоисточников — космических мазеров, радиопульсаров и др. Так, с помощью этого метода удалось измерить расстояние до объекта Стрелец B2 — газопылевого облака с бурным звездообразованием, находящимся в 100-120 парсеках от центра нашей Галактики. Результаты измерений показали, что Стрелец B2 расположен на расстоянии 7,8±0,8 кпк, что даёт расстояние до центра Галактики 7,9±0,8 кпк. Измерение параллаксов ультракомпактных внегалактических радиоисточников является одной из целей планируемого российского космического эксперимента Миллиметрон — космической обсерватории миллиметрового, субмиллиметрового и инфракрасного диапазонов.

Сравнение гелиоцентрической и геоцентрической системы мира

Годичный параллакс (звездный параллакс) даже у ближайших звезд не превышает одной угловой секунды. В связи с этим его измерение стало возможным лишь после изобретения оптических инструментов – телескопов. Сама возможность существования этого явления стала причиной принципиальных разногласий между геоцентрической и гелиоцентрической системами мира – геоцентрическая система считала, что Солнце обращается вокруг Земли. В то же время сторонники гелиоцентрической системы в течение почти 2 тысяч лет объясняли ненаблюдаемость звездных параллаксов огромными расстояниями до звезд. Первые попытки измерения звездных параллаксов были предприняты древнегреческим астрономом Аристархом Самосским в 3-ем веке нашей эры (считается, что он первым выдвинул предположения о гелиоцентрической системе мира). Позже такие попытки были предприняты Н. Коперником, Т. Браге, Г. Галилео, У. Гершелем и т.д. Последний во время попыток обнаружения звездных параллаксов случайно открыл неизвестную планету Солнечной Системы – Уран. По иронии судьбы, к тому времени, когда в начале 19 века всё же удалось измерить первые параллаксы звезды, сомнений в справедливости гелиоцентрической системы мира уже не оставалось. Так в ходе безуспешных попыток измерить параллакс у звезды Гамма Дракона (Этамин) английский астроном Джеймс Бредли (1692-1762 годы) в 1727 году открыл явление аберрации света, которая вызвана орбитальным движением Земли вокруг Солнца. Аберрация света представляет собой изменение видимого положения звезд примерно на 50 угловых секунд по причине конечной скорости света (первооткрыватель годичной аберрация определил скорость света в 308 тысяч км в секунду). Одновременно Д.Бредли получил верхний предел для звездных параллаксов в 0.5 угловой секунды. С другой стороны в попытках измерить звездные параллаксы, другому английскому астроному Уильяму Гершелю (1738-1822 году) в 1803 году удалось впервые зарегистрировать орбитальное движение двойных звезд (ранее предполагалось, что визуальные двойные звезды являются результатом случайности). Кроме того У. Гершель первым определил на основе наблюдаемых собственных движений звезд, что Солнечная Система движется в сторону созвездия Геркулеса.

Впервые факт отсутствия неизменности положения звезд на земном небе был обнаружен ещё Гиппархом на основе сверки положения ярких звезд его каталога, состоящего из примерно тысячи звезд с более древними каталогами вавилонян и александрийских астрономов. Гиппарх обнаружил систематическое изменение долготы положения звезд примерно на один градус (в то время как широта звезд относительно эклиптики оставалась неизвестной). Ныне это явление называется прецессией земной оси с периодом в 26 тысяч лет. Истинное движение звезд было впервые обнаружено в 1718 году английским астрономом Эдмондом Галлеем (1656-1743). В процессе уточнения прецессии Э. Галилей сравнил положения звезд из каталога Гиппарха с современными звездными каталогами. Сравнение показало, что на фоне большинства звезд, у которых положение на земном небе менялось согласно прецессии, встречался ряд аномалий (для Сириуса, Арктура и Альдебарана). У этих звезд отклонения в положении в несколько раз превысили погрешность измерений.

Как измеряется расстояние до звезд и что такое световой год?

Расстояния между звездами настолько велики, что измерять их километрами или милями – занятие с бесконечными нолями. Привычную систему измерений применяют для обозначения расстояний в одной системе. К примеру называют, что минимальное расстояние от Земли до Марса – 55,76 миллионов километров. Со звездами всё сложнее, и здесь обычно используют понятия светового года и парсека.

Астрономическая единица – принятая в астрономии единица измерения объектов Солнечной системы и ближайших к ней объектов Вселенной. Астрономическая единица равна 149 598 100 км (+- ~750 км), что приблизительно равняется среднему расстоянию Земли от Солнца. Современные наблюдения зафиксировали постепенно увеличение значения на 15 см ежегодно, что объясняется, возможной потерей Солнцем массы, последствия солнечного ветра.

Световой год – расстояние, которое свет проходит за один год, в метрах это 9 460 730 472 580 800. На самом деле свет звезд, который мы видим в безоблачную ночь, шёл до нашей планеты многие столетия, а некоторые из них вообще больше не существуют.

Парсек, он же «параллакс угловой секунды» – это расстояние, с которого средний радиус орбиты Земли (перпендикулярный лучу зрения), виден под углом в одну секунду угловую. Если совсем просто, то парсек = 3,26 световым годам.

Интересно то, что в научно-популярной и фантастической литературе принято использовать понятие светового года, а парсеками обычно пользуются только в профессиональных трудах и исследованиях.

Ближайшая к нам звезда – это Альфа Центавра, которая находится от Земли на расстоянии в 4,37 световых лет. А вот до самой удалённой галактики (по состоянию на декабрь 2012 года) от Земли целых 13,3 миллиардов световых лет!. Получается, когда солнце этой самой галактики (известной под индексом UDFj-39546284) потухнет, человечество об этом узнает еще не скоро.

Расстояния в цифрах

Меркурий– ближайшая к Солнцу планета, среднее расстояние от Солнца 0,387 а. е (58 млн. км), а расстояние до Земли колеблется от 82 до 217 млн. км. Меркурий движется вокруг Солнца по сильно вытянутой эллиптической орбите, плоскость которой наклонена к плоскости эклиптики под углом 7°.
Венера– вторая по удаленности от Солнца планета, среднее расстояние от Солнца 0,72 а.е. (108,2 млн. км). Средний радиус планеты составляет 6051 км, масса – 4,9 на 10 в 24 степени кг (0,82 массы Земли), средняя плотность 5,24 г/см3.
Земля– третья от Солнца планета Солнечной системы, среднее расстояние от Солнца 1 а.е. (149,6 млн. км), средний радиус 6371,160 км (экваториальный 6378, 160 км, полярный 6356,777 км), масса – 6 на 10 в 24 степени кг.
Марс– четвертая планета от Солнца, среднее расстояние от Солнца составляет 1,5 а.е. (227,9 млн. км). Минимальное расстояние от Марса до Земли составляет 55,75 млн. км, максимальное – около 401 млн. км.
Юпитер– пятая по счету от Солнца, а также крупнейшая планета Солнечной системы, среднее расстояние от Солнца 5,2 а.е.(778 млн. км), экваториальный радиус равен 71,4 тыс. км, полярный – около 67 тысяч км, масса 1,9 на 10 в 27 степени кг (317,8 массы Земли), средняя скорость обращения вокруг Солнца – 13,06 км/с.
Сатурн– шестая планета от Солнца и вторая по размерам планета в Солнечной системе после Юпитера. Среднее расстояние Сатурна от Солнца 9,54 а.е. (1,427 млрд. км), средний экваториальный радиус около 60,3 тысяч км, полярный – около 54 тысяч км, масса 5,68 на 10 в 26 степени кг (95,1 массы Земли).
Уран– седьмая от Солнца планета Солнечной системы. Планета была открыта в 1781 году английским астрономом Уильямом Гершелем и названа в честь греческого бога неба Урана. Среднее расстояние от Солнца 19,18 а.е. (2871 млн. км), средний радиус 25560 км, масса 8,69 на 10 в 25 степени (14,54 массы Земли), средняя плотность – 1,27 г/см3.
Нептун– восьмая планета от Солнца и четвертая по размеру среди планет. Нептун открыт в Берлинской обсерватории 23 сентября 1846 года немецким астрономом Иоганном Галле на основании предсказаний, сделанных независимо математиком Джоном Адамсом в Англии и астрономом Урбеном Леверрье во Франции. Среднее расстояние планеты Нептун от Солнца 30,1 а.е. (4497 млн. км), средний радиус около 25 тысяч км, масса 1,02 на 10 в 26 степени кг (17,2 массы Земли), плотность 1,64 г/см3.
Плутоном– в честь древнеримского бога подземного царства. В тот момент предполагали, что его масса сравнима с массой Земли, но позже было установлено, что масса Плутона почти в 500 раз меньше земной, даже меньше массы Луны. Масса Плутона 1,2 на 10 в22 степени кг (0,22 массы Земли). Среднее расстояние Плутона от Солнца 39,44 а.е. (5,9 на 10 в12 степени км), радиус около 1,65 тысяч км.

Литература

Берри А. [www.astro-cabinet.ru/library/Berri/Index.htm Краткая история астрономии]. — 2-е изд. — М.-Л.: Гостехиздат, 1946. — 363 с.
Веселовский И. Н. [www.astro-cabinet.ru/library/Aristarch/Aristarch_3.htm Аристарх Самосский — Коперник античного мира] // Историко-астрономические исследования3, вып. VII. — М., 1961. — С. 17—70.
Ерпылев Н. П. [www.astro-cabinet.ru/library/IAI_4/Iai_Ogl.htm Развитие звездной астрономии в России в XIX в] // Историко-астрономические исследования, вып. IV. — М., 1958. — С. 13—88.
Ефремов Ю. Н. Вглубь Вселенной. — М.: УРСС, 2003. — 263 с.
Житомирский С. В. [astro-cabinet.ru/library/IAI_16/Iai_Ogl.htm Античные представления о размерах мира] // Историко-астрономические исследования, вып. XVI. — М., 1983. — С. 291—326.
Ковалевский Ж. Современная астрометрия. — Фрязино: Век 2, 2004. — 480 с.
Лавринович К. К. [www.astro-cabinet.ru/library/IAI_17/Iai_Ogl.htm Фридрих Вильгельм Бессель (1784—1846). К 200-летию со дня рождения] // Историко-астрономические исследования, вып. XVII. — М., 1984. — С. 285—322.
Лавринович К. К. Фридрих Вильгельм Бессель. — М.: Наука, 1989. — 320 с. — ISBN 5-02-005884-X.
Паннекук А. [www.astro-cabinet.ru/library/Pannekuk/Index.htm История астрономии]. — М.: Наука, 1966. — 592 с.
// Энциклопедический словарь юного астронома / сост. Н. П. Ерпылев. — М.: Педагогика, 1986. — С. 207—208. — 336 с.
Africa T. W. Copernicus’ Relation to Aristarchus and Pythagoras // Isis. — 1961. — Vol. 52. — P. 406—407.
Dyson F. W. Measurement of the distances of the stars (англ.) // The Observatory (англ.)русск.. — 1915. — Vol. 38. — P. 292—299. — .
Hirshfeld A. W. Parallax: The Race to Measure the Cosmos. — Courier Dover Publications, 2013. — ISBN 0-7167-3711-6.
Hoskin M. A. Stellar distances: Galileo’s method and it’s subsequent history // Indian Journal for the History of Science. — 1966. — Vol. 1. — P. 22—29.
Van Helden A. Measuring the Universe. Cosmic dimensions from Aristarchus to Halley. — Chicago & London: The University of Chicago Press, 1985.

Астрономия

Учебник для 10 класса

§22.2. Годичный параллакс и расстояния до звезд

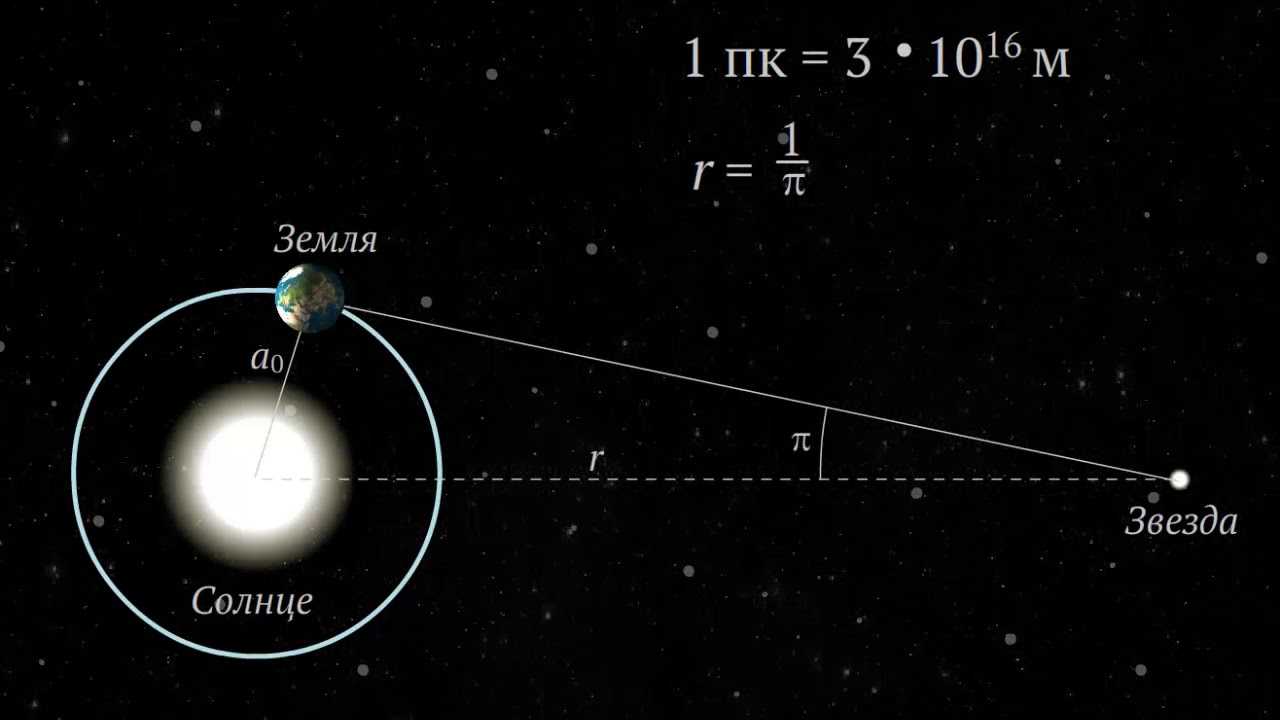
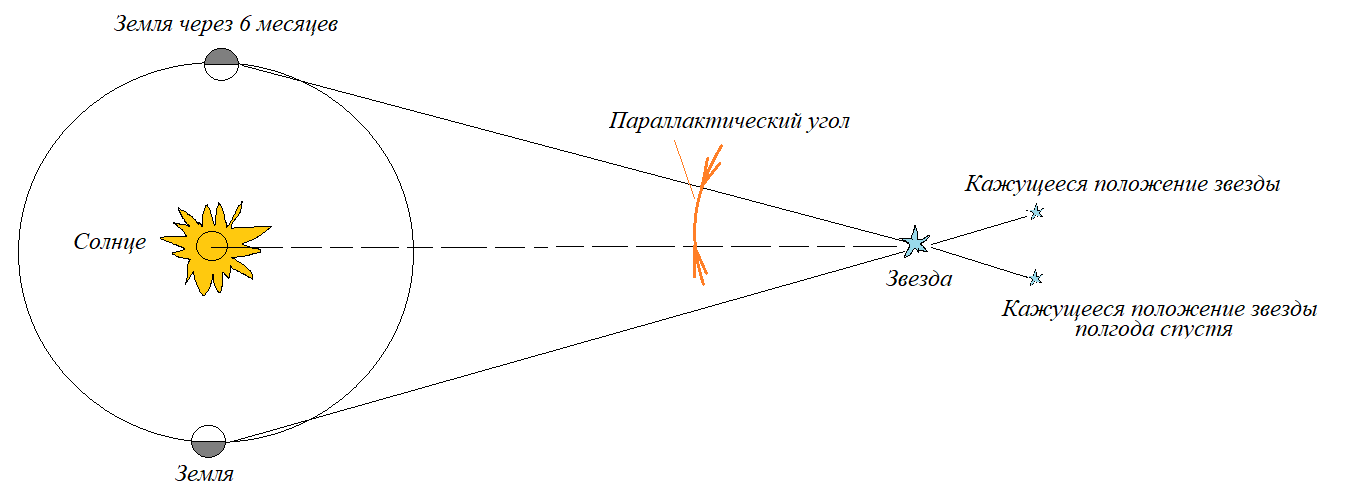
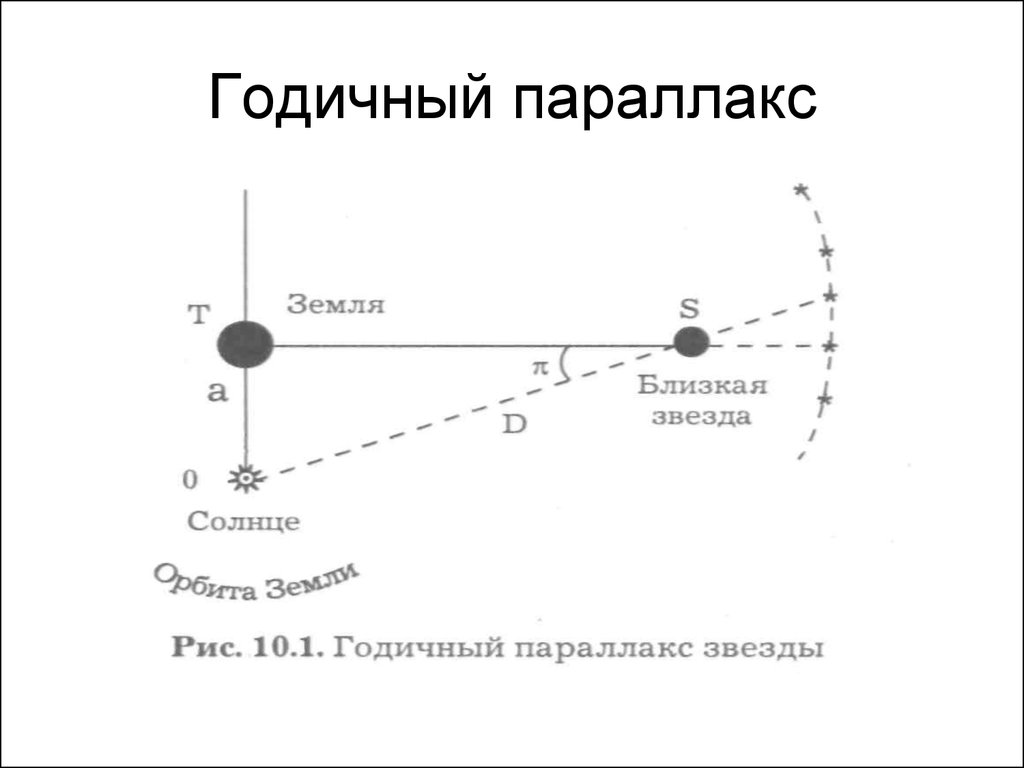
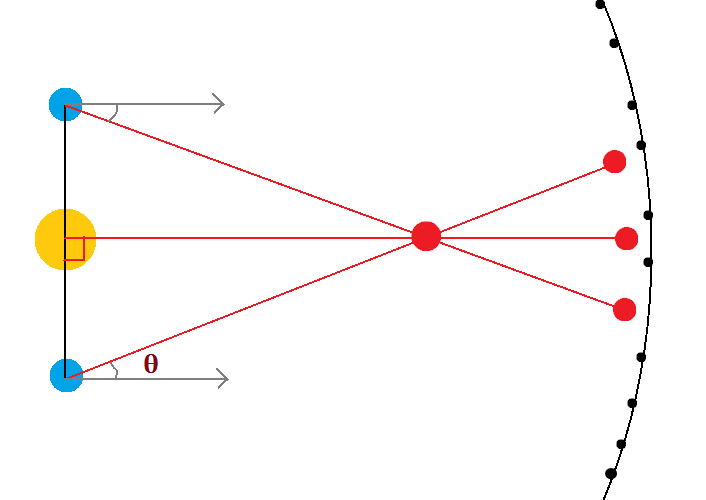
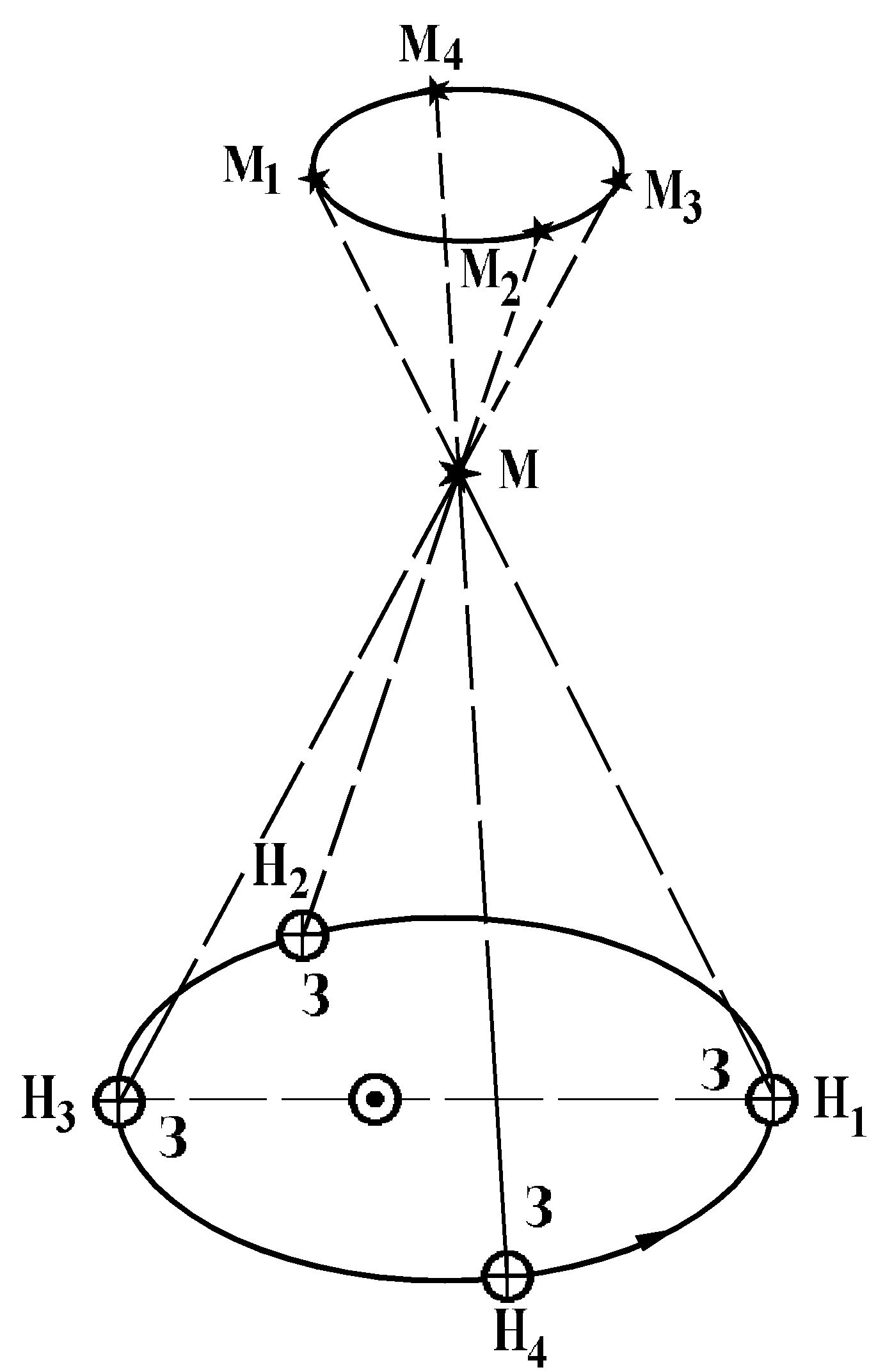
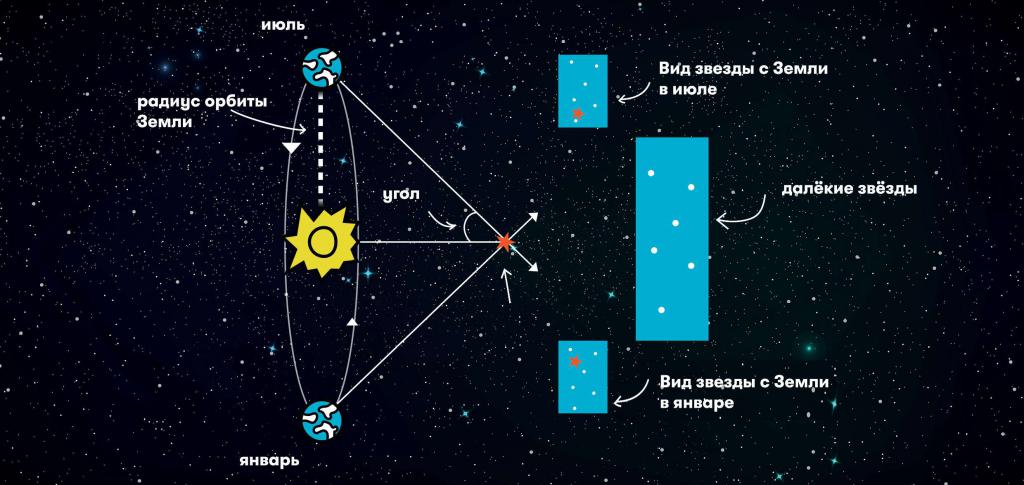
Радиус Земли оказывается слишком малым, чтобы служить базисом для измерения параллактического смещения звезд и для определения расстояний до них. Еще во времена Коперника было ясно, что если Земля действительно перемещается в пространстве, обращаясь вокруг Солнца, то видимые положения звезд на небе должны меняться. Земля за полгода перемещается на величину диаметра своей орбиты. Направления на звезду с двух концов диаметра этой орбиты должны различаться на величину параллактического смещения. Иначе говоря, у звезд должен быть заметен годичный параллакс. Годичным параллаксом звезды р называют угол, под которым со звезды можно было бы видеть большую полуось земной орбиты (равную 1 а. е.), если она перпендикулярна лучу зрения (рис. 79).

Чем больше расстояние D до звезды, тем меньше ее параллакс (рис. 79). Параллактическое смещение положения звезды на небе в течение года происходит по маленькому эллипсу или кругу, если звезда находится в полюсе эклиптики (см. рис. 79).

Рис. 79. Годичные параллаксы звезд.

Для определения годичного параллакса измеряют направление на звезду в различные моменты времени, когда Земля находится в разных точках своей орбиты. Параллакс легче всего измерить если моменты наблюдений разделены примерно полугодом. За это время Земля переносит наблюдателя на расстояние, равное диаметру ее орбиты.

Параллакс звезд долго не могли обнаружить, и Коперник правильно утверждал, что звезды слишком далеки от Земли, чтобы существовавшими тогда приборами можно было обнаружить параллактическое смещение звезд при базисе, равном диаметру земной орбиты. (Подсчитайте, во сколько раз он больше, чем диаметр Земли.) В настоящее время способ определения годичного параллакса является основным при определении расстояний до звезд, и уже измерены параллаксы для нескольких тысяч звезд.

Впервые годичный параллакс звезды был надежно измерен выдающимся русским ученым В. Я. Струве в 1837 г. Он измерил годичный параллакс звезды Веги. Почти одновременно в других странах измерили параллаксы еще у двух звезд. Одной из них была а Центавра. Эта звезда южного полушария неба и в СССР не видна. Она оказалась ближайшей к нам звездой с годичным параллаксом р = 0,75″. Под таким углом невооруженному глазу видна проволочка толщиной 1 мм с расстояния 280 м. Неудивительно, что так долго не могли заметить у звезд подобные столь малые угловые смещения.

Расстояние до звезды

где а — большая полуось земной орбиты. Если принять а за единицу и учесть, что при малых углах

то получим:

астрономических единиц.

Расстояние до ближайшей звезды а Центавра D = 206 265″: 0,75″ = 270 000 а. е. Свет проходит расстояние до а Центавра за 4 года, тогда как от Солнца до Земли он идет только 8 мин а от Луны около 1 с.

Расстояния до звезд удобно выражать в парсеках (пк).

Парсек — расстояние, с которого большая полуось земной орбиты, перпендикулярная лучу зрения, видна под углом в 1″. Расстояние в парсеках равно обратной величине годичного параллакса, выраженного в секундах дуги. Например, расстояние до звезды а Центавра равно 0,75″ (3/4″) или 4/3 пк.

1 парсек = 3,26 светового года = 3 • 1013 км.

Измерением годичного параллакса можно надежно установить расстояние до звезд, находящихся не далее 100 пк, или 300 световых лет. Расстояния до более далеких звезд в настоящее время определяют другими методами (см. § 24.1).