Энтропия

В химии

Что такое, к примеру, энтропия в химии? Это понятие применяется в химической термодинамике

Здесь важно изменение этой величины. Если оно положительно, то и система становится менее упорядоченной

Знать это важно для определения направления химических реакций и изменения химического равновесия. Этот термин связан с понятием энтальпии — энергии, которую можно превратить в тепло при определенном постоянном давлении.

По изменению неупорядоченности можно определить, может ли реакция протекать самопроизвольно. Этого нельзя сделать только по изменению энергии, так как существуют и реакции, протекающие с поглощением тепла, и реакции, протекающие с его выделением. Согласно второму началу термодинамики, состояние с наибольшей неупорядоченностью — это наиболее устойчивое состояние замкнутой системы. Также любая замкнутая система стремится к наименее упорядоченному состоянию. Поэтому при самопроизвольных процессах беспорядок возрастает.

Виды энтропий

Этот термин используется в термодинамике, экономике, теории информации и даже в социологии. Что же он определяет в этих областях?

В физической химии (термодинамике)

Основной постулат термодинамики о равновесии: любая изолированная термодинамическая система приходит в равновесное состояние с течением времени и не может из него выйти самопроизвольно. То есть каждая система стремится в равновесное для неё состояние. И если говорить совсем простыми словами, то такое состояние характеризуется беспорядком.

Энтропия — это мера беспорядка. Как определить беспорядок? Один из способов — приписать каждому состоянию число вариантов, которыми это состояние можно реализовать. И чем больше таких способов реализации, тем больше значение энтропии. Чем больше организованно вещество (его структура), тем ниже его неопределённость (хаотичность).

Абсолютное значение энтропии (S абс.) равно изменению имеющейся у вещества или системы энергии во время теплопередачи при данной температуре. Его математическая величина определяется из значения теплопередачи (Q), разделённого на абсолютную температуру (T), при которой происходит процесс: S абс. = Q / T. Это означает, что при передаче большого количества теплоты показатель S абс. увеличится. Тот же эффект будет наблюдаться при теплопередаче в условиях низких температур.

В экономике

В экономике используется такое понятие, как коэффициент энтропии. С помощью этого коэффициента исследуют изменение концентрации рынка и её уровень. Чем выше значение коэффициента, тем выше экономическая неопределённость и, следовательно, вероятность появления монополии снижается. Коэффициент помогает косвенно оценить выгоды, приобретённые фирмой в результате возможной монопольной деятельности или при изменении концентрации рынка.

В статистической физике или теории информации

Информационная энтропия (неопределённость)— это мера непредсказуемости или неопределённости некоторой системы. Эта величина помогает определить степень беспорядочности проводимого эксперимента или события. Чем больше количество состояний, в которых может находиться система, тем больше значение неопределённости. Все процессы упорядочивания системы приводят к появлению информации и снижению информационной неопределённости.

С помощью информационной непредсказуемости можно выявить такую пропускную способность канала, которая обеспечит надёжную передачу информации (в системе закодированных символов). А также можно частично предсказывать ход опыта или события, деля их на составные части и высчитывая значение неопределённости для каждой из них. Такой метод статистической физики помогает выявить вероятность события. С его помощью можно расшифровать закодированный текст, анализируя вероятность появления символов и их показатель энтропии.

Существует такое понятие, как абсолютная энтропия языка. Эта величина выражает максимальное количество информации, которое можно передать в единице этого языка. За единицу в этом случае принимают символ алфавита языка (бит).

В социологии

Здесь энтропия (информационная неопределённость) является характеристикой отклонения социума (системы) или его звеньев от принятого (эталонного) состояния, а проявляется это в снижении эффективности развития и функционирования системы, ухудшении самоорганизации. Простой пример: сотрудники фирмы так сильно загружены работой (выполнением большого количества отчётов), что не успевают заниматься своей основной деятельностью (выполнением проверок). В этом примере мерой нецелесообразного использования руководством рабочих ресурсов будет являться информационная неопределённость.

Автоматизированные тесты

Решение

из-за недостаточного тестирования было потеряно 1,3 млрд клиентских записей

• «Тестирование замедляет всех и везде».
• «Мы стартап, у нас нет времени на тесты».
• «Тестирование для шимпанзе. Я знаю, что делаю, потому что у меня большой мозг».

• Тесты покажут упущенные вами баги. Составьте их список, чтобы показать принимающим решения, какие проблемы могут возникнуть у компании без тестов.
• Все будут увереннее изменять приложение. Разработчики будут тратить меньше времени, спрашивая себя, не сломают ли их изменения что-нибудь другое.
• Не нужно тестировать вручную каждое изменение. Ручное тестирование — это настоящая потеря времени, и нужно всячески его минимизировать.
• Автоматические тесты покажут, есть ли какие-то системные проблемы в вашем коде. Например, если тесты трудно писать из-за обилия зависимостей. В таком случае исправляйте архитектуру!
• Тесты могут помочь понять, как должен работать ваш код. Подумайте о своих коллегах!

уменьшит у всех стресссвоём выступлении

• Заняться с коллегами совместным программированием, чтобы показать, чем полезны тесты и как легко их можно писать.
• Организовать встречу с командой и предложить какой-то базовый процесс тестирования, который вы сможете со временем адаптировать под ваши команды.

Берт Рутан

В физике

Этот термин используется в таких разделах физики, как термодинамика и статистическая физика. Термодинамика изучает способы передачи и превращения энергии. Она имеет дело с процессами, в которых можно использовать понятие температуры. Именно в термодинамике впервые начали использовать это понятие. Ввел его немецкий ученый Рудольф Клаузиус. Статистическая механика изучает поведение систем из конечного количества частиц, используя для этого методы теории вероятности.

В разных разделах физики этот термин означает несколько разные вещи. В термодинамике это характеристика необратимого рассеяния энергии. В статистической физике эта величина показывает вероятность какого-то состояния.

В термодинамике

Энтропия — единственная величина, показывающая направление физических процессов. Что это значит?

• В изолированной системе, то есть той, которая не обменивается ни веществом, ни энергией с окружающими предметами, процессы всегда идут так, что неупорядоченность увеличивается. Достигнув максимума, она остается постоянной. В этом суть второго начала термодинамики.
• Обратимые процессы не меняют неупорядоченность.
• Необратимые процессы всегда идут так, что беспорядок увеличивается. В открытой системе эта величина может возрастать или оставаться постоянной, возможны и такие процессы, при которых беспорядок уменьшается. То есть вмешательством извне мы можем уменьшить неупорядоченность.

Всякая система, находящаяся в неизменных внешних условиях, со временем приходит в состояние равновесия и не может самостоятельно из него выйти. При этом все ее части будут иметь одинаковую температуру. Это нулевое начало термодинамики.

В равновесии беспорядок больше всего. Например, есть сосуд, разделенный перегородкой. С одной стороны находится один газ, с другой — другой. Если убрать перегородку, постепенно газы смешаются и самостоятельно уже не разделятся снова. Такое состояние будет более беспорядочным, чем состояние, когда газы были разделены.

• температуры;
• давления;
• объема;
• внутренней энергии.

В статистической механике

В статистической механике это понятие связано с вероятностью получить определенное состояние. Например, для нескольких предметов или частиц она зависит от числа способов их расположить.

Есть несколько определений этой величины. Наиболее простое определение Больцамана. Она равна логарифму вероятности состояния, умноженному на постоянную Больцмана: S=k*ln(W).

Энтропия растет. Энтропия растёт в изолированных системах?

Пять мифов о развитии и энтропии. Миф третий.Храним мы под замком надёжным деньги, продукты прячем от тепла во льду.Но человеку жить в уединенье и взаперти совсем невмоготу.Второе начало термодинамики утверждает, что энтропия в изолированной системе не убывает, то есть сохраняется или растёт. А может ли она расти вне изолированной системы?Сразу заметим, что термин «система» в формулировке второго начала используется лишь для краткости. Под ним понимается любое множество элементов, тогда как система включает связи между ними и предполагает некоторую целостность. И связи, и целостность могут лишь замедлять рост энтропии, исключая некоторые (возможно, нежелательные для системы) состояния. Ни в каких других отношениях системность для второго начала не важна.Требование изолированности возникает из-за того, что из открытой системы энтропия может экспортироваться и рассеиваться в окружающей среде. Но, после того, как изолированное множество элементов уравновесилось, пришло в наиболее вероятное макросостояние, энтропия, достигнув максимума, далее расти не может.Рост энтропии возможен лишь при наличии какой-либо неравновесности, которая не возникнет, пока не возобновится приток энергии извне или отток её наружу. Недаром мы помещаем вещи в изолированные хранилища – это препятствует внешним воздействиям, способствующим возникновению неравновесности и дальнейшему росту энтропии. Поэтому изолированность, как и системность, не способствует росту энтропии, а лишь гарантирует её неубывание. Именно вне изолированной системы, в открытой среде, преимущественно и происходит рост энтропии.Хотя классическая формулировка второго начала не говорит, как изменяется энтропия в открытых системах и средах, это не является большой проблемой. Достаточно мысленно отделить участок среды или группу открытых систем, участвующих в процессе и не испытывающих внешних воздействий и считать их единой изолированной системой. Тогда их суммарная энтропия не должна убывать. Так рассуждали, к примеру, У. Эшби, оценивая воздействие одной системы на другую, и И. Пригожин при рассмотрении диссипативных структур.Хуже то, что большой класс процессов, в которых энтропия растёт, а именно процессов накопления нарушений в системах под влиянием внешних сил, как бы выходит из-под действия второго начала – ведь они не могут идти в изолированных системах!Поэтому лучше было бы сформулировать закон так: любой самопроизвольный процесс преобразования энергии, массы, информации не уменьшает общей энтропии всех связанных с ним систем и частей среды. В такой формулировке снимается избыточное требование системности, изолированность обеспечивается учётом всех участвующих в процессе элементов и утверждается справедливость закона для всех самопроизвольных процессов.

Примечания

1. Зубарев Д. Н., Морозов В. Г. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
2. Сивухин Д. В. Общий курс физики. — М., 1979. — Т. II. Термодинамика и молекулярная физика. — С. 127.
3. , с. 77.
4. Зубарев Д. Н., Морозов В. Г. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
5. Энтропия //  :  / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
6. , с. 468—475.
7. , с. 13—22, 108-125.
8. Джейнс Э. Т. О логическом обосновании методов максимальной энтропии // ТИИЭР. — 1982. — Т. 70, вып. 9. — С. 33—51.
9. , с. 29—39.

Энтропия: определение и история появления термина

История появления термина

Энтропия как определение состояния системы была введена в 1865 году немецким физиком Рудольфом Клаузиусом, чтобы описать способность теплоты превращаться в другие формы энергии, главным образом в механическую. С помощью этого понятия в термодинамике описывают состояние термодинамических систем. Приращение этой величины связано с поступлением тепла в систему и с температурой, при которой это поступление происходит.

Определение термина из Википедии

Этот термин долгое время использовался только в механической теории тепла (термодинамике), для которой оно вводилось. Но со временем это определение перешло в другие области и теории. Существует несколько определений термина «энтропия».

Википедия даёт краткое определение для нескольких областей, в которых этот термин используется:«Энтропия (от др.-греч. ἐντροπία «поворот»,«превращение») — часто употребляемый в естественных и точных науках термин. В статистической физике характеризует вероятность осуществления какого-либо макроскопического состояния. Помимо физики, этот термин широко используется в математике: теории информации и математической статистике».

Абсолютное значение

Энтропия — величина неотрицательная (больше или равна нулю). Чем ближе температура к абсолютному нулю, тем она тоже ближе к нулю. Это третье начало термодинамики. В первоначальном виде его сформулировал Макс Планк в 1911 году.

Также третье начало термодинамики называют принципом недостижимости абсолютного нуля. Это значит, что при любых процессах, связанных с изменением неупорядоченности, невозможно достигнуть абсолютного нуля (0К, или -273,15 С). Можно только бесконечно приближаться к этой температуре. Ученые договорились, что при 0 К неупорядоченность равна 0.

В термодинамике обычно не имеет значения абсолютная величина, важно только ее изменение. Однако можно найти и абсолютное значение

Оно вычисляется по разным формулам для твердого, жидкого и газообразного состояния вещества. Эта величина измеряется в Дж/К или Дж/градус, то есть в тех же единицах, что и теплоемкость. Удобно поделить эту величину на массу или количество моль вещества. Поэтому используют единицы Дж/(моль*К) или Дж/(моль*градус) в зависимости от того, в чем измеряется температура — в кельвинах или градусах.

Что называют «энтропией» на простом языке?

«Entropia«, в переводе с греческого поворот, превращение. Это слово можно определить, как меру беспорядка, стремление к хаосу. Для точного определения энтропии используются математические расчеты. Лучше всего ее эффект показывают примеры термодинамики, в которых процесс перехода тепла в механическую работу не является абсолютным. Часть его будет преобразована в другие виды энергии.

Совсем простой пример энтропии

Представим подготовку квартиры или офиса к праздничному мероприятию. Все вымыто, аккуратно разложено, столы накрыты, стулья расставлены. Получилась маленькая энтропия. Праздник идет по полной программе. Танцы, хлопушки, фейерверки! Гости расходятся. В квартире полный хаос. Вы получаете систему с большим показателем энтропии. Надо приводить помещение в порядок. Вы тратите на уборку свои силы, энергию. Через время величина энтропии в системе снижается. Порядок восстановлен. И все в соответствии со вторым законом термодинамики. Была добавлена энергия извне. И система теперь не может считаться изолированной.

Рудольф Клаузиус и Людвиг Больцман об энтропии

Термин entropia, впервые введенный немецким ученым Рудольфом Клаузисом в 1865-ом г., применялся для объяснения невозможности передачи теплоты из холодного в более теплое тело. Смысл термина определял «уход в себя” или “вовнутрь”. Идея “ухода в себя” в свою очередь заинтересовала учёного из Австрии Людвига Больцмана. Он провел ряд исследовательских работ и дал следующее разъяснение процесса энтропии.

Возьмем за основу любую систему. Например, газ в сосуде. Он имеет ряд характеристик, которые показывают его макросостояние:

• температура;
• давление;
• объем.

• расположение частиц;
• скорость движения частиц.

Состояние системы непрерывно меняется. Это стремление к неорганизованности, к увеличению энтропии. И, одновременно, происходит поиск системой своего самого возможного состояния — равновесия. Следовательно, когда мы говорим о росте энтропии, это означает, что эта система пытается прийти к равновесию.

Вне зависимости от того, насколько хаотично будет происходить движение частиц в сосуде, скорость их движения всегда будет приближена к средней величине. В этом случае, энтропия будет максимальной.

Таким образом, считает Больцман, значение энтропии определяет вероятность микросостояния тела.

Энтропия и «демон Максвелла”

Классический пример “демона” рассматривался неоднократно в различных научных работах и трудах. Есть простое и ясное описание его сути данное «отцом кибернетики” Нобертом Винером. Рассмотрим резервуар, наполненный газом. Температура внутри его будет одинаковая. Скорость движения некоторого числа молекул газа больше, чем остальных.

https://youtube.com/watch?v=hG2bhaRk98c

Добавим в конструкцию тепловой двигатель и две трубы. Соединим резервуар и тепловой двигатель трубой. Вторая труба соединит выходное отверстие двигателя и газовую камеру. Входы из резервуара в двигатель и из двигателя в камеру снабдим маленькими дверцами, возле которых будут сидеть маленькие «демоны”. Их задача открыть или закрыть дверцу в зависимости от того как будут двигаться молекулы.

Первый демон будет открывать дверь только молекулам, имеющим большую скорость. Второй пропустит только самые медленные частицы. Итог работы — температура в резервуаре возле первого демона повысится, возле второго — понизится. Получаем источник абсолютно полезной энергии из случайного движения.

Связь между энтропией и информацией

“Демоны” смогли понизить уровень энтропии. Хотя по законам физики, она должна возрастать. С этим парадоксом справился уже венгерский физик Л. Сциллард. Его работа завершила исследование Максвелла.
Во время своей работы демон использует дополнительные силы, которые он тратит на усилия открыть или закрыть дверь. Демон снижает энтропию, но рассчитывается за процесс информации — можно ли пропустить данную частицу, своей энергией.
Мы получаем доказательство, что информация и энтропия неразрывно связаны между собой. Соответственно информация имеет обратную зависимость от энтропии. С помощью информации мы определяем направление движения частиц, определяем их скорость, производим оценку их движения. Под это правило подойдет любая другая категория. Например: разный смысл букв или символов.

На основании этих выводов, К Шеннон стал создателем формулы энтропии, применяемой для учета информации, где первая является мерой хаоса, вторая же несет в себе упорядоченность.

Употребление в различных дисциплинах

• Термодинамическая энтропия — термодинамическая функция, характеризующая меру необратимой диссипации энергии в ней.
• В статистической физике — характеризует вероятность осуществления некоторого макроскопического состояния системы.
• В математической статистике — мера неопределённости распределения вероятностей.
• Информационная энтропия — в теории информации мера неопределённости источника сообщений, определяемая вероятностями появления тех или иных символов при их передаче.
• Энтропия динамической системы — в теории динамических систем мера хаотичности в поведении траекторий системы.
• Дифференциальная энтропия — формальное обобщение понятия энтропии для непрерывных распределений.
• Энтропия отражения — часть информации о дискретной системе, которая не воспроизводится при отражении системы через совокупность своих частей.
• Энтропия в теории управления — мера неопределённости состояния или поведения системы в данных условиях.

В термодинамике

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при замкнутых обратимых процессах, тогда как в необратимых замкнутых — её изменение всегда положительно. В открытой системе может происходить уменьшение энтропии рассматриваемой системы за счет уноса энергии, например в виде излучения, при этом полная энтропия окружающей среды увеличивается.

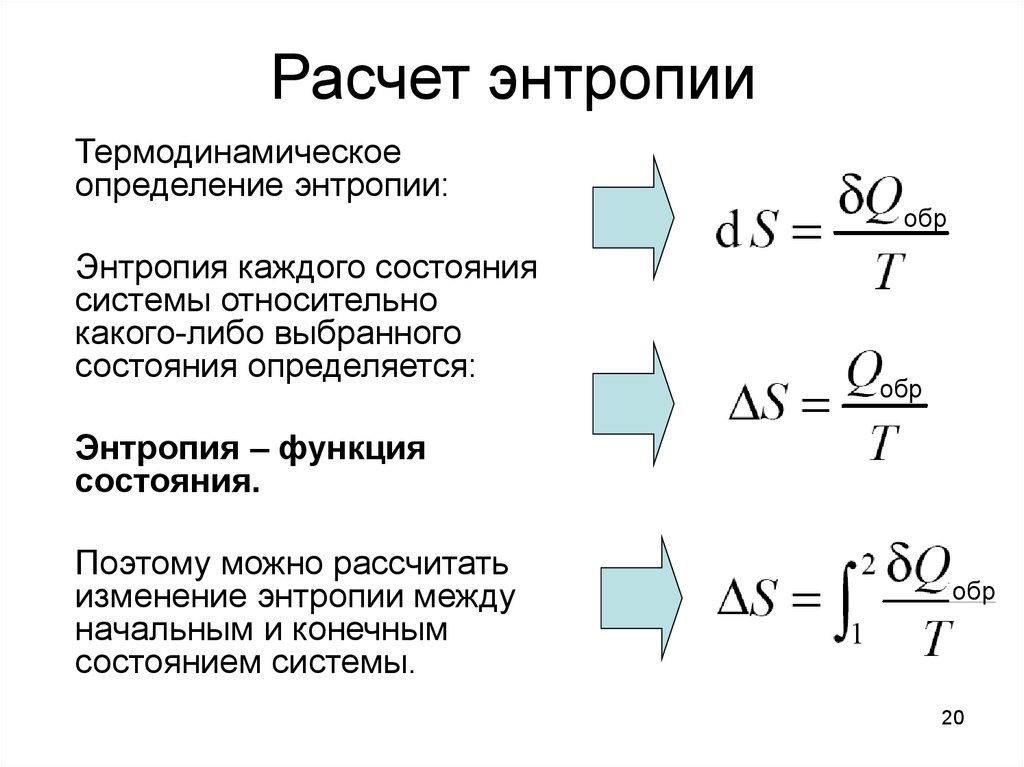
Математически энтропия определяется как функция состояния системы, определённая с точностью до произвольной постоянной. Разность энтропий в двух равновесных состояниях 1 и 2, по определению, равна приведённому количеству тепла (δQT{\displaystyle \delta Q/T}), которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути:

ΔS1→2=S2−S1=∫1→2δQT{\displaystyle \Delta S_{1\to 2}=S_{2}-S_{1}=\int \limits _{1\to 2}{\frac {\delta Q}{T}}}.

(1)

Так как энтропия определена с точностью до произвольной постоянной, то можно условно принять состояние 1 за начальное и положить S1={\displaystyle S_{1}=0}. Тогда

S=∫δQT{\displaystyle S=\int {\frac {\delta Q}{T}}},

(2.)

Здесь интеграл берется для произвольного квазистатического процесса. Дифференциал функции S{\displaystyle S} имеет вид

dS=δQT{\displaystyle dS={\frac {\delta Q}{T}}}.

(3)

Энтропия устанавливает связь между макро- и микро- состояниями. Особенность данной характеристики заключается в том, что это единственная функция в физике, которая показывает направленность процессов. Поскольку энтропия является функцией состояния, то она не зависит от того, как осуществлён переход из одного состояния системы в другое, а определяется только начальным и конечным состояниями системы.

Аксиоматическое определение энтропии

Выражение для информационной энтропии может быть выведено на основе некоторой системы аксиом. Одним из подходов является следующая система аксиом, известная как система аксиом Хинчина.

1. Пусть некоторая система может пребывать в каждом из N{\displaystyle N} доступных состояний с вероятностью pi{\displaystyle p_{i}}, где i=1,…,N{\displaystyle i=1,…,N}. Энтропия H{\displaystyle H} является функцией только вероятностей P=(p1,…,pN){\displaystyle P=(p_{1},…,p_{N})}: H=H(P){\displaystyle H=H(P)}.

2. Для любой системы P{\displaystyle P} справедливо H(P)≤H(Punif){\displaystyle H(P)\leq H(P_{unif})}, где Punif{\displaystyle P_{unif}} — система с равномерным распределением вероятностей: p1=p2=…=pN=1N{\displaystyle p_{1}=p_{2}=…=p_{N}=1/N}.

3. Если добавить в систему состояние pN+1={\displaystyle p_{N+1}=0}, то энтропия системы не изменится.

4. Энтропия совокупности двух систем P{\displaystyle P} и Q{\displaystyle Q} имеет вид H(PQ)=H(P)+H(QP){\displaystyle H(PQ)=H(P)+H(Q/P)}, где H(QP){\displaystyle H(Q/P)} — средняя по ансамблю P{\displaystyle P} условная энтропия Q{\displaystyle Q}.

Указанный набор аксиом однозначно приводит к формуле для энтропии Шеннона.

Некоторые авторы обращают внимание на неестественность последней аксиомы Хинчина. И действительно, более простым и очевидным является требование аддитивности энтропии для независимых систем

Таким образом, последняя аксиома может быть заменена следующим условием.

4′. Энтропия совокупности двух независимых систем P{\displaystyle P} и Q{\displaystyle Q} имеет вид H(PQ)=H(P)+H(Q){\displaystyle H(PQ)=H(P)+H(Q)}.

Оказывается, система аксиом с пунктом 4′ приводит не только к энтропии Шеннона, но и к энтропии Реньи.

Так что же такое энтропия?

Если в двух словах, то

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.

Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).

Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

S = log Ω

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.

Людвиг Больцман

Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть определённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

Энтропия Вселенной

Рудольф Клаузиус

В результате возникновения такого понятия как энтропия появилось множество других утверждений и физических определений, которые позволили подробнее описать законы природы. Одним из них есть такое понятие как «обратимые/необратимые процессы». К первым относят процессы, энтропия системы которых не возрастает и остается постоянной. Необратимые – такие процессы, в замкнутой системе которых энтропия растет. Вернуть замкнутую систему в состояние до процесса невозможно, т.к. в таком случае энтропия должна была бы понижаться.

По мнению Клаузиуса, необратимым процессом является существование Вселенной, в конце которого ее ждет так называемая «Тепловая смерть», иначе – термодинамическое равновесие, существующее для закрытых систем. То есть энтропия достигнет максимального показателя, а все процессы просто затухнут. Но, как вскоре оказалось, Рудольф Клаузиус не учитывал силы гравитации, которые присутствуют повсеместно во Вселенной. К примеру, благодаря ним распределение частиц при максимальной энтропии не обязано быть однородным.

Также к другим недостаткам теории о «тепловой смерти Вселенной» можно отнести тот факт, что нам неизвестно действительно ли она конечна, и можно ли к ней применить понятие «замкнутая система». Стоит учитывать и то, что состояние максимальной энтропии, как собственно и абсолютный вакуум – такие же теоретические понятия, как и идеальный газ. Это означает, что в реальности энтропия не будет достигать максимального значения, из-за различных случайных отклонений.

Примечательно то, что видимая Вселенная в своем объеме сохраняет значение энтропии. Причиной тому служит уже известный для многих феномен – расширение Вселенной. Это интересное совпадение в очередной раз доказывает человечеству то, что в природе ничего не происходит просто так. Согласно подсчетам ученых, по порядку величины значение энтропии равняется количеству существующих фотонов.

Перемешивание газов

И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Фридрих 1. Биография

Коронация Фридриха в кирхе Кёнигсбергского замка

Фридрих, сын курфюрста Бранденбургского Фридриха Вильгельма, прозванного Великим курфюрстом, родился в Кёнигсберге 11 июля 1657 года от первой жены своего отца — Луизы-Генриетты. Смерть старшего брата, Карла-Эмиля в 1674 году, открыла ему путь к короне.

Слабый здоровьем, бесхарактерный, легко поддававшийся влияниям, он был склонен к пышности и блеску. Поразительное различие между ним и отцом его отмечено всеми историками — различие в характере, воззрениях и стремлениях. Лавис метко называет Фридриха блудным сыном в семье скупцов. Наряду со страстью к роскоши стояло поклонение Фридриха III всему французскому. В «Deutsch-französische Modegeist» 1689 года говорится: «Теперь все должно быть французским: французский язык, французская одежда, французская кухня, посуда, французские танцы, французская музыка и французская болезнь. Гордый, лживый, развратный французский дух совершенно усыпил немцев». На содержание двора тратилось в год до 820 000 талеров, то есть всего на 10 000 талеров меньше, чем на содержание всего гражданского управления государства. Фридрих II характеризовал своего деда словами: «Великий в малых делах и малый в великих».

Энтропия Вселенной

Величина	Формула расчета	Значение
Полная энтропия видимой части S{\displaystyle S}	4π3sγlH03{\displaystyle {\frac {4\pi }{3}}s_{\gamma }l_{H_{0}}^{3}}	∼1088{\displaystyle \sim 10^{88}}
Удельная энтропия фотонного газа sγ{\displaystyle s_{\gamma }}	8π290T03{\displaystyle {\frac {8\pi ^{2}}{90}}T_{0}^{3}}	≈1.5103{\displaystyle \approx 1.510^{3}} см-3

Энтропия Вселенной  — величина, характеризующая степень неупорядоченности и тепловое состояние Вселенной . Классическое определение энтропии и способ её вычисления не подходят для Вселенной, так как в оной действуют силы гравитации, и вещество само по себе не образует замкнутой системы . Однако можно доказать, что в сопутствующем объёме полная энтропия сохраняется .

В сравнительно медленно расширяющейся Вселенной энтропия в сопутствующем объёме сохраняется, а по порядку величины энтропия равна числу фотонов.

Закон сохранения энтропии во Вселенной

В общем случае, приращение внутренней энергии имеет вид:

Учтем, что химический потенциал частиц равны по значению и противоположны по знаку:

Если считать расширение равновесным процессом, то последние выражение можно применить к сопутствующему объёму ( V∝a3{\displaystyle V\propto a^{3}} , где a{\displaystyle a} — «радиус» Вселенной). Однако, в сопутствующем объёме разница частиц и античастиц сохраняется. Учитывая этот факт, имеем:

Но причиной изменения объёма является расширение. Если теперь, учитывая это обстоятельство, продифференцировать по времени последнее выражение:

Теперь, если подставить уравнение неразрывности, входящую в систему:

Последнее означает, что энтропия в сопутствующем объёме сохраняется.