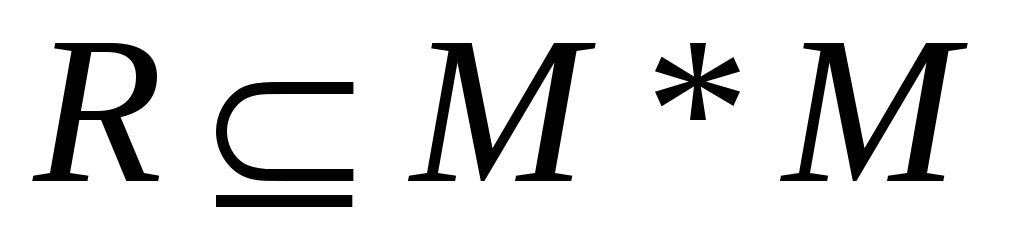В чем разница между равенством и эквивалентностью?

Связанные определения

Классом эквивалентности a⊂X{\displaystyle \subset X} элемента a∈X{\displaystyle a\in X} называется подмножество элементов, эквивалентных a{\displaystyle a}; то есть,

a={x∈X∣x∼a}{\displaystyle =\{\,x\in X\mid x\sim a\,\}}.

Из вышеприведённого определения немедленно следует, что если b∈a{\displaystyle b\in }, то a=b{\displaystyle =}.

Фактормножество — множество всех классов эквивалентности заданного множества X{\displaystyle X} по заданному отношению ∼{\displaystyle \sim }, обозначается X∼{\displaystyle X/{\sim }}.

Для класса эквивалентности элемента a{\displaystyle a} используются следующие обозначения: a{\displaystyle }, a∼{\displaystyle a/{\sim }}, a¯{\displaystyle {\overline {a}}}.

Множество классов эквивалентности по отношению ∼{\displaystyle \sim } является разбиением множества.

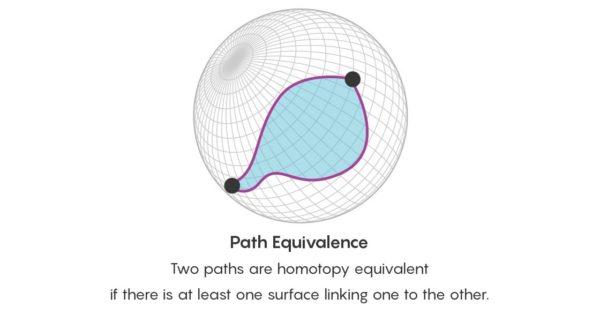
Что такое эквивалентность?

К сожалению, в толковом словаре Ожегова не указано значение данного термина, поэтому обратимся к значениям однокоренных с ним («эквивалент» и «эквивалентный»), которые удалось найти в толковом словаре, и на их основе составим определение слова «эквивалентность».

• Эквивалент — это нечто равноценное другому, вполне заменяющее его.
• Эквивалентный — вполне равноценный чему-н. в каком-н. отношении.

Таким образом, можно сказать, что эквивалентность — это равноценность в каком-либо отношении. Употребление термина допустимо при описании равноценного замещения или же просто равноценности.

Самые распространённые синонимы к слову: отношение, равенство, одинаковость, равносильность, равнозначность, равноценность, идентичность.

Антонимы: различие, неэквивалентность, неравноценность, неравносильность.

Слово употребляется редко, преимущественно в литературе и научно-публицистических текстах. В разговорной речи термин практически не используется.

Связанные определения

Классом эквивалентности a⊂X{\displaystyle \subset X} элемента a∈X{\displaystyle a\in X} называется подмножество элементов, эквивалентных a{\displaystyle a}; то есть,

a={x∈X∣x∼a}{\displaystyle =\{\,x\in X\mid x\sim a\,\}}.

Из вышеприведённого определения немедленно следует, что если b∈a{\displaystyle b\in }, то a=b{\displaystyle =}.

Фактормножество — множество всех классов эквивалентности заданного множества X{\displaystyle X} по заданному отношению ∼{\displaystyle \sim }, обозначается X∼{\displaystyle X/{\sim }}.

Для класса эквивалентности элемента a{\displaystyle a} используются следующие обозначения: a{\displaystyle }, a∼{\displaystyle a/{\sim }}, a¯{\displaystyle {\overline {a}}}.

Множество классов эквивалентности по отношению ∼{\displaystyle \sim } является разбиением множества.

Эквивалент в окислительно-восстановительных реакциях

Фактор эквивалентности соединений в окислительно-восстановительных реакциях равен:

f_экв(X) = 1/n,                (2.5)

где n – число отданных или присоединенных электронов.

Для определения фактора эквивалентности рассмотрим три уравнения реакций с участием перманганата калия:

2KMnO₄ + 5Na₂SO₃ + 3H₂SO₄ = 5Na₂SO₄ + 2MnSO₄ + K₂SO₄ + 3H₂O.

2KMnO₄ + 2Na₂SO₃ + H₂O = 2Na₂SO₄ + 2MnO₂ + 2KOH.

2KMnO₄ + Na₂SO₃ + 2NaOH = Na₂SO₄ + K₂MnO₄ + Na₂MnO₄ + H₂O.

В результате получаем следующую схему превращения KMnO₄.

в кислой среде: Mn+7 + 5e = Mn+2

в нейтральной среде: Mn+7 + 3e = Mn+4

в щелочной среде: Mn+7 + 1e = Mn+6

 Схема превращений KMnO₄ в различных средах

Таким образом, в первой реакции f_экв(KMnO₄) = 1/5, во второй – f_экв(KMnO₄) = 1/3, в третьей – f_экв(KMnO₄) = 1.

Следует подчеркнуть, что фактор эквивалентности дихромата калия, реагирующего в качестве окислителя в кислой среде, равен 1/6:

Cr₂O₇2- + 6e + 14H+ = 2 Cr3+ + 7H₂O

Эквивалент в кислотно-основных реакциях

На примере взаимодействия ортофосфорной кислоты со щелочью с образованием дигидро-, гидро- и среднего фосфата рассмотрим эквивалент вещества H₃PO₄.

H₃PO₄ + NaOH = NaH₂PO₄ + H₂O, f_экв(H₃PO₄) =1.

H₃PO₄ + 2NaOH = Na₂HPO₄ + 2H₂O, f_экв(H₃PO₄) =1/2.

H₃PO₄ + 3NaOH = Na₃PO₄ + 3H₂O, f_экв(H₃PO₄) =1/3.

Эквивалент NaOH соответствует формульной единице этого вещества, так как фактор эквивалентности NaOH равен единице. В первом уравнении реакции молярное соотношение реагентов равно 1:1, следовательно, фактор эквивалентности H₃PO₄ в этой реакции равен 1, а эквивалентом является формульная единица вещества H₃PO₄.

Во втором уравнении реакции молярное отношение реагентов H₃PO₄ и NaOH составляет 1:2, т.е. фактор эквивалентности H₃PO₄ равен 1/2 и её эквивалентом является 1/2 часть формульной единицы вещества H₃PO₄ .

В третьем уравнении реакции количество веществ реагентов относятся друг к другу как 1:3. Следовательно, фактор эквивалентности H₃PO₄ равен 1/3, а её эквивалентом является 1/3 часть формульной единицы вещества H₃PO₄.

Таким образом, эквивалент вещества зависит от вида химического превращения, в котором принимает участие рассматриваемое вещество.

Следует обратить внимание на эффективность применения закона эквивалентов: стехиометрические расчёты упрощаются при использовании закона эквивалентов, в частности, при проведении этих расчётов отпадает необходимость записывать полное уравнение химической реакции и учитывать стехиометрические коэффициенты. Например, на взаимодействие без остатка 0,25 моль-экв ортофосфата натрия потребуется равное количество эквивалентов вещества хлорида кальция, т.е. n(1/2CaCl2) = 0,25 моль

В каких случаях слово «эквивалентность» не стоит менять на «равенство»?

Когда нужно указать на неточное совпадение величин. Например:

• Высота Останкинской телебашни в Москве эквивалентна высоте Всемирного торгового центра в Нью-Йорке. Нельзя: высота Останкинской телебашни в Москве равна высоте Всемирного торгового центра в Нью-Йорке. (Потому что высоты двух башен в точности не совпадают). Но можно: высота Останкинской телебашни в Москве примерно равна высоте Всемирного торгового центра в Нью-Йорке.
• Количество снега, выпавшего в этом году, эквивалентно количеству снега, выпавшего в прошлом. Нельзя: количество снега, выпавшего в этом году, равно количеству снега, выпавшего в прошлом. (Потому что в точности количества не совпадают). Но можно: количество снега, выпавшего в этом году, приближенно равно количеству снега, выпавшего в прошлом.

См. также

• Военное снаряжение
• Разгрузочный жилет
• Средства индивидуальной защиты
• Класс опасности
• Амуниция
• British Army uniform and equipment in World War I  (англ.)
• List of uniforms and clothing of World War II  (англ.)
• Sniper equipment  (англ.)
• Военная форма
• Солдат будущего

Примеры

• Равенство («={\displaystyle \;=}»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
• Сравнение по модулю, («а ≡ b (mod n)»).
• В евклидовой геометрии
  • Отношение конгруэнтности («≅{\displaystyle \cong }»).
  • Отношение подобия (« ∼{\displaystyle \ \sim }»).
  • Отношение параллельности прямых («‖{\displaystyle \|}»).
• Эквивалентность функций в математическом анализе:

  Говорят, что функция f(x){\displaystyle f(x)} эквивалентна функции g(x){\displaystyle g(x)} при x→x{\displaystyle x\rightarrow x_{0}}, если она допускает представление вида f(x)=α(x)g(x){\displaystyle f(x)=\alpha (x)g(x)}, где α(x)→1{\displaystyle \alpha (x)\rightarrow 1} при x→x{\displaystyle x\rightarrow x_{0}}. В этом случае пишут f(x)∼g(x){\displaystyle f(x)\sim g(x)}, напоминая при необходимости, что речь идёт о сравнении функций при x→x{\displaystyle x\rightarrow x_{0}}. Если g(x)≠{\displaystyle g(x)\neq 0} при x≠x{\displaystyle x\neq x_{0}}, эквивалентность функций f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} при x→x{\displaystyle x\rightarrow x_{0}}, очевидно, равносильна соотношению limx→xf(x)g(x)=1{\displaystyle \lim _{x\rightarrow x_{0}}{\frac {f(x)}{g(x)}}=1}.

• на векторном пространстве.
• Отношение равномощности множеств.
• Изоморфизм групп, колец, векторных пространств
• Эквивалентность категорий.
• в некоторой категории задаёт отношение эквивалентности на этой категории.