Доверительный интервал

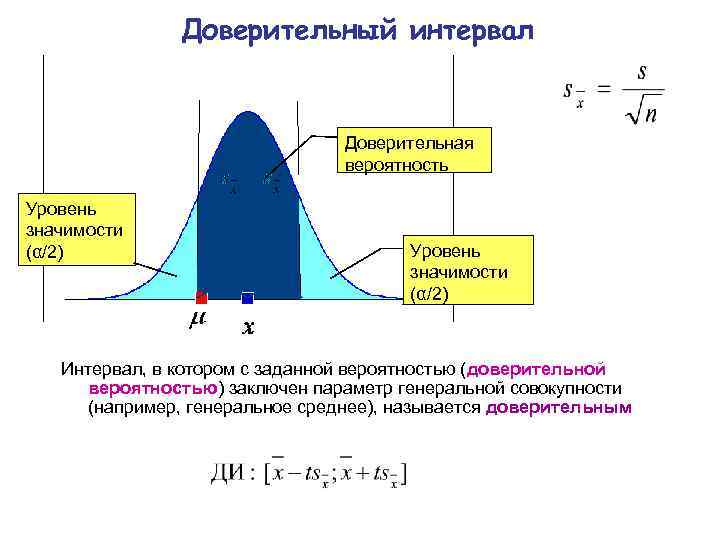
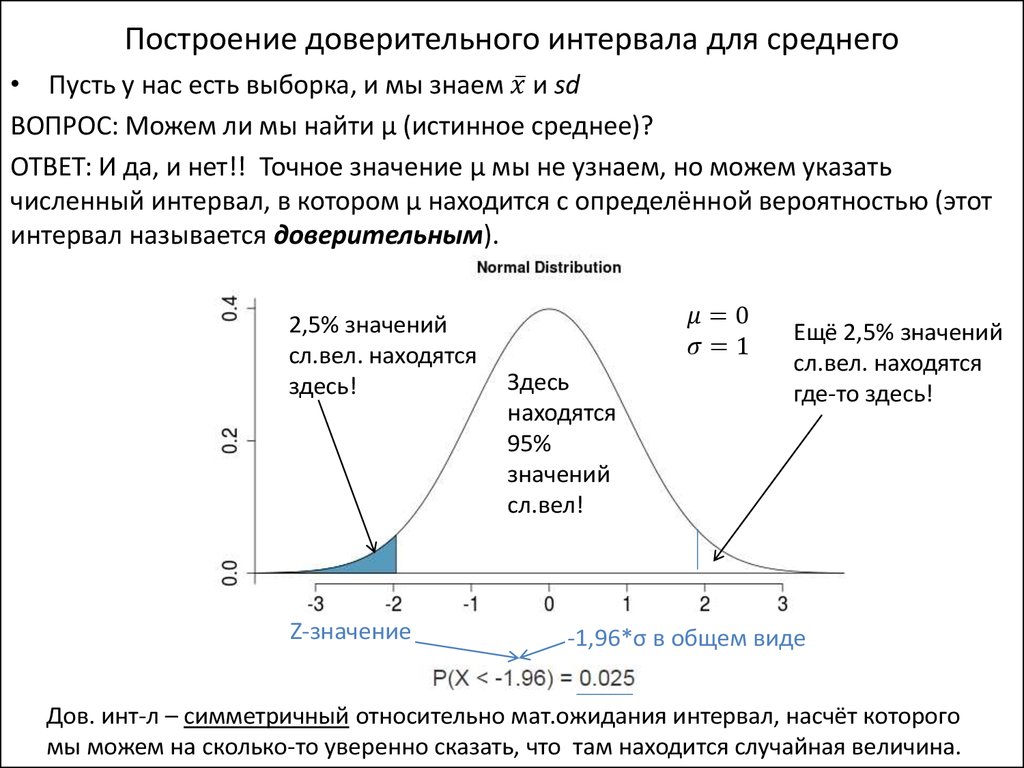
Как построить доверительный интервал нормального распределения в Excel

Поскольку интервал значений, в котором находится некоторая неизвестная величина, совпадает с областью, в которой могут изменяться значения этой величины, то вероятность правильности оценки данной величины стремится к нулю. Поэтому, принято устанавливать определенное значение вероятности для нахождения границ изменения некоторой величины. Значения, находящиеся между этими границами, называют доверительным интервалом.

Примечание:

Рассматриваемая функция была заменена функцией ДОВЕРИТ.НОРМ с версии Excel 2010. Функция ДОВЕРИТ была оставлена для обеспечения совместимости с документами, созданными в более ранних версиях табличного редактора.

Библиография

• Рыбак, Р.А. (1956) Статистические Методы и Научный Вывод. Оливер и Бойд, Эдинбург. (См. p. 32.)
• Freund, J.E. (1962) Математическая Статистика Прентис Хол, Энглвудские Утесы, Нью-Джерси (См. стр 227-228.)
• Взламывание, я. (1965) логика статистического вывода. Издательство Кембриджского университета, Кембридж. ISBN 0-521-05165-7
• Хранение, E.S. (1962) введение в статистический вывод. Д. ван Нострэнд, Принстон, Нью-Джерси
• Мейо, D. G. (1981) «В защиту теории Неимен-Пирсона доверительных интервалов», Философия науки, 48 (2), 269–280.
• Неимен, J. (1937) «Схема Теории Статистической Оценки, Основанной на Классической Теории Вероятности» Философские Сделки Королевского общества Лондона A, 236, 333–380. (Оригинальная работа.)
• Дикарь, Л. Дж. (1962), фонды статистического вывода. Метуэн, Лондон.
• Смитсон, M. (2003) Доверительные интервалы. Количественные Применения в Ряду Общественных наук, № 140. Белмонт, Калифорния: Публикации SAGE. ISBN 978-0-7619-2499-9.
• Мехта, S. (2014) ISBN тем статистики 978-1499273533

Практический пример доверительного интервала

Клиническое исследование оценило связь между наличием астмы и риском развития обструктивного апноэ сна у взрослых.

Некоторые взрослые были случайным образом набраны из списка государственных служащих, за которыми следили в течение четырех лет.

Участники с астмой, по сравнению с теми, у кого нет, имели более высокий риск развития апноэ через четыре года.

При проведении клинических исследований, подобных этому примеру, подмножество интересующей группы населения обычно привлекается для повышения эффективности исследования (меньше затрат и меньше времени).

Эта подгруппа лиц, изучаемая популяция, состоит из тех, кто соответствует критериям включения и согласен участвовать в исследовании, как показано на рисунке ниже.

Затем исследование завершается и рассчитывается величина эффекта (например, средняя разница или относительный риск ), чтобы ответить на вопрос исследования.

Этот процесс, называемый выводом, включает использование данных, собранных у исследуемой совокупности, для оценки величины фактического воздействия на представляющую интерес совокупность, то есть совокупность происхождения.

В приведенном примере исследователи набрали случайную выборку государственных служащих (исходная популяция), которые имели право и согласились участвовать в исследовании (исследуемая популяция), и сообщили, что астма увеличивает риск развития апноэ в исследуемой популяции.

Чтобы учесть ошибку выборки из-за набора только подгруппы представляющего интерес населения, они также рассчитали 95% доверительный интервал (около оценки) от 1, 06 до 1, 82, что указывает на вероятность 95 %, что истинный относительный риск в исходной популяции будет между 1, 06 и 1, 82 .

Общий обзор

Взяв выборку из популяции, мы получим точечную оценку интересующего нас параметра и вычислим стандартную ошибку для того, чтобы указать точность оценки.

Однако, для большинства случаев стандартная ошибка как такова не приемлема. Гораздо полезнее объединить эту меру точности с интервальной оценкой для параметра популяции.

Это можно сделать, используя знания о теоретическом распределении вероятности выборочной статистики (параметра) для того, чтобы вычислить доверительный интервал (CI – Confidence Interval, ДИ – Доверительный интервал) для параметра.

Вообще, доверительный интервал расширяет оценки в обе стороны некоторой величиной, кратной стандартной ошибке (данного параметра); два значения (доверительные границы), определяющие интервал, обычно отделяют запятой и заключают в скобки.

Что такое доверительный интервал:

Это оценка диапазона, используемого в статистике, который содержит параметр совокупности. Этот неизвестный параметр популяции находится в выборочной модели, рассчитанной на основе собранных данных .

Пример: среднее значение выборки x̅ может соответствовать или не соответствовать истинному среднему значению для населения µ. Для этого можно рассмотреть диапазон выборочных средств, в которых может содержаться это среднее значение. Чем длиннее этот интервал, тем больше вероятность этого.

Доверительный интервал выражается в процентах, обозначенных уровнем достоверности, причем 90%, 95% и 99% являются наиболее указанными. Например, на изображении ниже мы имеем 90% доверительный интервал между его верхним и нижним пределами (a и -a ).

Доверительный интервал является одним из наиболее важных понятий в рамках проверки гипотез в статистике, поскольку он используется в качестве меры неопределенности. Термин был введен польским математиком и статистиком Ежи Нейманом в 1937 году.

Как интерпретировать доверительный интервал?

Правильная интерпретация доверительного интервала, вероятно, является наиболее сложным аспектом этой статистической концепции. Примером наиболее распространенной интерпретации концепции является следующее:

Существует 95% вероятность того, что в будущем истинное значение параметра совокупности (например, среднее значение) попадет в диапазон X (нижний предел) и Y (верхний предел).

Таким образом, доверительный интервал интерпретируется следующим образом: он на 95% уверен, что интервал между X (нижняя граница) и Y (верхняя граница) содержит истинное значение параметра совокупности.

Было бы совершенно неверно утверждать, что: существует 95% вероятность того, что интервал между X (нижняя граница) и Y (верхняя граница) содержит реальное значение параметра совокупности.

Вышеприведенное утверждение является наиболее распространенным заблуждением о доверительном интервале. После расчета статистического диапазона он может содержать только параметр совокупности или нет.

Тем не менее, интервалы могут варьироваться между выборками, в то время как истинный параметр популяции одинаков независимо от выборки.

Следовательно, доверительный интервал доверительного интервала может быть сделан только в случае, когда доверительные интервалы пересчитываются для количества выборок.

5.2.3. Доверительный интервал для среднего. Точный смысл

Возьмем выборку объема 121 испытаний нормально распределенной случайной величины с математическим ожиданием 177 и среднеквадратическим отклонением 11. 5-процентный квантиль распределения Стьюдента для 120 степеней свободы равен 1.98 (почти не отличаясь от квантиля нормального распределения, как мы говорили). Стандартная ошибка для получаемых случайных выборок будет колебаться около ​\( 11/\sqrt{121} \)​, т.е. вокруг единицы. Таким образом, радиус доверительного интервала будет колебаться около 1.98. На рис. 5.2.3(1). показаны результаты 100 испытаний такой процедуры: порождалась выборка объема 121, оценивалось стандартное отклонение, вычислялся доверительный интервал и он изображался вертикальным отрезком. Жирными линиями выделены те экземпляры доверительных интервалов, которые не накрыли математическое ожидание 177.

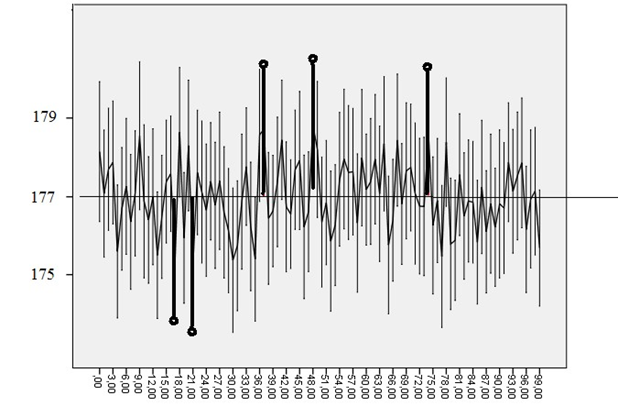
Рис. 5.2.3(1). Результат моделирования последовательного порождения выборок объема 121 испытаний нормальной случайной величины с математическим ожиданием 177 и среднеквадратическим отклонением 11. Построено 100 доверительных интервалов. Жирной линией выделены те, которые не накрывают математическое ожидание 177

В литературе встречаются следующие интерпретации доверительного интервала (не все они правильные):

1. 95%-й доверительный интервал для среднего с вероятностью 0.95 накрывает истинное математическое ожидание.
2. Истинное математическое ожидание с вероятностью 0.95 содержится в доверительном интервале.
3. 95% средних значений новых выборок попадут в полученный нами интервал.

Истинность первого утверждения мы можем проиллюстрировать нашим примером на . Действительно, если математическое ожидание нам известно, то 95%-й доверительный интервал будет накрывать его в среднем в 95% случаев.

Вторая формулировка тем не менее не истинна: если мы получили какой-то доверительный интервал, то ничего о вероятности попадания истинного математического ожидания в этот интервал мы сказать не можем. Прежде всего, потому что истинное математическое ожидание не является случайной величиной . Далее, если вы знаете истинное математическое ожидание роста случайно выбранного жителя Томска, а я оцениваю его по выборке, то вы всегда знаете, получил ли я «счастливый» или «несчастливый» интервал, а я не могу этого знать. В «несчастливом» случае на мое заявление «истинное математическое ожидание с вероятностью 0.95 содержится в (полученном мной) доверительном интервале» вы со стопроцентной уверенностью скажете, что оно там не содержится и никогда не будет содержаться.

Третья формулировка ложна в силу тех же обстоятельств. «Несчастливый» интервал накрывает меньше даже той половины оси, в которой он разместился. Вероятность попадания среднего в другую половину оси равна 0.5. Несчастливый интервал не обещает даже 50-процентной вероятности попадания в него будущих средних выборочных.

Итак, верно лишь первое утверждение — в том смысле, который прояснен на : известное кому-то (в худшем случае, одному богу) математическое ожидание накрывается доверительным интервалом с соответствующей вероятностью.

Следующая формулировка еще точнее: если мы собираемся оценить истинное среднее по выборке, то вероятность того, что 95%-й доверительный интервал, который мы по выборке построим, накроет истинное среднее, равна 0.05

Здесь важно, что вероятность вообще касается только тех событий, которые еще не произошли

>> следующий параграф>>

В таблице мы обозначили возможные значения случайной величины буквами a, чтобы отличать их от результатов испытаний этой случайной величины (выборочных значений), по-прежнему обозначаемых буквами x.

 Если в последней формуле заменить строчные буквы x заглавными, то полученная формула задаст случайную величину, подобно тому, как в предыдущем параграфе  рассматривалась как случайная величина. Напомним: при большом объеме выборки эта случайная величина имеет стандартное нормальное распределение. Если выборка невелика, то распределение «расплывается» (как изображено на ) и квантили надо определять по соответствующим распределениям Стьюдента.

 Только в искусственных ситуациях можно сделать истинное математическое ожидание случайной величиной, но это потребует задать его априорное распределение.

Способы расчета доверительного интервала

Смысл вычисления доверительного интервала заключается в построении по данным выборки такого интервала, чтобы можно было утверждать с заданной вероятностью, что значение оцениваемого параметра находится в этом интервале. Другими словами, доверительный интервал с определенной вероятностью содержит неизвестное значение оцениваемой величины. Чем шире интервал, тем выше неточность.

Существуют разные методы определения доверительного интервала. В этой статье рассмотрим 2 способа:

• через медиану и среднеквадратическое отклонение;
• через критическое значение t-статистики (коэффициент Стьюдента).

Этапы сравнительного анализа разных способов расчета ДИ:

1. формируем выборку данных;

2. обрабатываем ее статистическими методами: рассчитываем среднее значение, медиану, дисперсию и т.д.;

3. рассчитываем доверительный интервал двумя способами;

4. анализируем очищенные выборки и полученные доверительные интервалы.

5.2.2. Доверительный интервал для среднего и значимость. Точные формулы

Пусть для некоторой выборки объема n мы получили ​\( \overline{x}=a \)​ и стандартное отклонение, равное s. Чтобы вычислить радиус доверительного интервала, надо сначала найти соответствующий квантиль распределения Стьюдента с ​\( n-1 \)​ степенями свободы ​\( t^{n-1}_\alpha \)​ (​\( \alpha=1-0.95 \)​  для 95%-го интервала, аналогично для интервалов других «номиналов»). Затем квантиль надо умножить на стандартную ошибку.

Итак, доверительный интервал уровня ​\( 1-\alpha \)​ для среднего по выборке объема n это интервал ​\( (\overline{x}-R_\alpha; \overline{x}+R_\alpha) \)​, где

\

Для оценки значимости гипотезы «истинное среднее равно a» необходимо рассчитать t-статистику по формуле

\

и оценить вес отсекаемого полученным результатом хвоста распределения Стьюдента с n−1 степенями свободы (и затем его удвоить, чтобы получить двухстороннюю значимость).

Упражнение 5.2.2(1). Убедиться, что если ​\( \overline{x}-a=R_\alpha \)​, то значимость соответствующей гипотезы «истинное среднее равно a» равна в точности α.

Этап 3. Расчёт доверительного интервала

Способ 1. Расчёт через медиану и среднеквадратическое отклонение.

Доверительный интервал определяется следующим образом: минимальное значение — из медианы вычитается СКО; максимальное значение – к медиане прибавляется СКО.

Формула доверительного интервала:

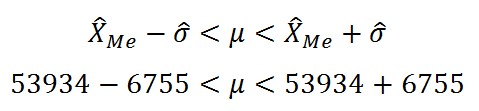
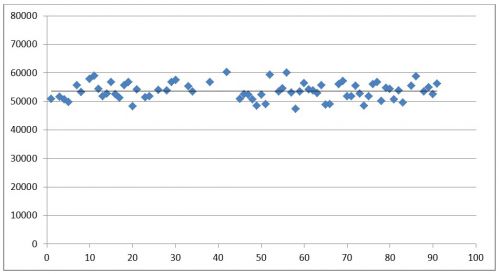
Таким образом, доверительный интервал (47179 д.е.; 60689 д.е.)

Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 20 объектов, что составило 22% выборки.

Рис. 2. Значения, попавшие в доверительный интервал 1.

Способ 2. Построение доверительного интервала через критическое значение t-статистики (коэффициент Стьюдента)

С.В. Грибовский в книге «Математические методы оценки стоимости имущества» описывает способ вычисления доверительного интервала через коэффициент Стьюдента. При расчете этим методом оценщик должен сам задать уровень значимости ∝, определяющий вероятность, с которой будет построен доверительный интервал. Обычно используются уровни значимости 0,1; 0,05 и 0,01. Им соответствуют доверительные вероятности 0,9; 0,95 и 0,99. При таком методе полагают истинные значения математического ожидания и дисперсии практически неизвестными (что почти всегда верно при решении практических задач оценки).

Формула доверительного интервала:

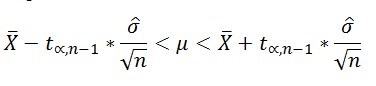
n — объем выборки;

— критическое значение t- статистики (распределения Стьюдента) с уровнем значимости ∝,числом степеней свободы n-1,которое определяется по специальным статистическим таблицам либо с помощью MS Excel (  →»Статистические»→ СТЬЮДРАСПОБР);

∝ — уровень значимости, принимаем ∝=0,01.

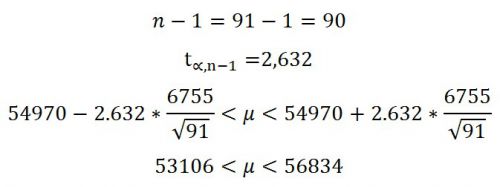
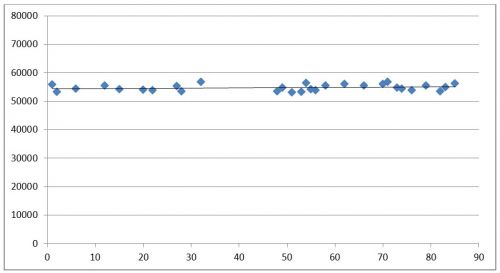
Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 62 объекта, что составило 68% выборки.

Рис. 2. Значения, попавшие в доверительный интервал 2.

5.2.1. Среднее выборочное как случайная величина

Напомним, что для случайной величины, заданной таблицей

X	a1	a2	…	an
	p1	p2	…	pn

математическое ожидание и дисперсия задаются формулами:

\

\

Напомним также формулы выборочного среднего и выборочной дисперсии:

\

\

В предыдущем параграфе мы говорили, что стандартная ошибка среднего для X, которой измеряется точность оценок, есть стандартное отклонение s, деленное на ​\( \sqrt{n} \)​.

Теперь мы разъясним смысл сказанного.

Когда мы планируем оценить средний рост томичей по выборке объема 100, мы заранее заготавливаем форму обработки выборки, которую еще предстоит получить. Можно сказать, что мы предполагаем совершить испытание случайной величины

\

которая представляет собой среднее арифметическое 100 экземпляров случайной величины X: «рост случайного взрослого мужчины-жителя Томска» (обратите внимание, что формула составлена из заглавных букв, которыми мы обозначаем случайные величины). По теореме о сложении дисперсий для суммы независимых случайных величин (см

подпараграф 3.2.5 и приложение 2), дисперсия числителя в правой части в 100 раз больше дисперсии X. Легко также увидеть непосредственно из вида формулы математического ожидания и дисперсии случайной величины, что для любой случайной величины Y/n (в том числе и для стократной суммы одинаковых величин, которая помещена в числителе последней формулы)

\[ M_{Y/n}=\frac{1}{n}M_Y \]

и

\[ D_{Y/n}=\frac{1}{n^2}D_Y \]

Первая формула достаточно очевидна. Используя ее, выводим вторую:

\[ D_{Y/n}=\frac{1}{n-1}[(a_1/n-M_Y)^2p_1+(a_2/n-M_Y)^2p_2+\dots+(a_n/n-M_Y)^2p_n)]= \]

\= \]

\=\frac{1}{n^2}D_Y \]

В таком случае ​\( M_{\overline{X}}=M_X \)​ и ​\( D_{\overline{X}}=\frac{1}{n}D_X \)​, а следовательно, среднеквадратическое отклонение делится на корень из n:  ​\( \sigma_{\overline{X}}=\sigma_X/\sqrt{n} \)​ т.е. среднеквадратическое отклонение среднего по n испытаниям случайной величины в ​\( \sqrt{n} \)​ раз меньше, чем среднеквадратическое отклонение данной случайной величины. Мы можем сказать теперь, что стандартная ошибка среднего оценивает среднеквадратическое отклонение случайной величины ​\( \overline{X} \)​.

Поскольку для любого нормального распределения с математическим ожиданием M и среднеквадратическим отклонением α вероятность попадания в интервал \( (M-\alpha;M+\alpha) \)​  постоянна (как и вероятности попадания в интервалы с радиусом, равным любому другому фиксированному кратному среднеквадратического отклонения), то среднее арифметическое при увеличении выборки стягивается сужающейся рамкой ​\( (M-\sigma/\sqrt{x};M+\sigma/\sqrt{x}) \)​ к реальному математическому ожиданию M.

Как посчитать доверительный интервал по функции ДОВЕРИТ в Excel

Функция имеет следующую синтаксическую запись:

=ДОВЕРИТ(альфа;стандартное_откл;размер)

Описание аргументов:

• альфа – обязательный, принимает числовое значение, характеризующее уровень значимости – вероятность отклонения нулевой (неверной) гипотезы в том случае, когда она на самом деле верна. Определяется как 1-, где  — уровень доверия (вероятность нахождения истинного значения некоторой оцениваемой величины в определенном интервале, называемом доверительным).
• стандартное_откл – обязательный, принимает значение стандартного отклонения величины для генеральной совокупности значений (в Excel предусмотрена функция для определения этой величины — СТАНДОТКЛОН.Г).
• размер – обязательный, принимает числовое значение, характеризующее количество точек данных в анализируемой выборке (ее размер).

Примечания:

1. Все аргументы функции должны указываться в виде числовых значений или данных, которые могут быть преобразованы в числа (например, текстовые строки с числами, логические ИСТИНА, ЛОЖЬ). В противном случае результатом выполнения функции ДОВЕРИТ будет код ошибки #ЧИСЛО!
2. Аргумент альфа должен быть указан числовым значением из диапазона от 0 до 1 (оба включительно). Иначе функция ДОВЕРИТ вернет код ошибки #ЧИСЛО! Аналогичная ошибка возникает в случаях, когда аргумент стандартное_откл задан числом, взятым из диапазона отрицательных значений или нулем.
3. Диапазон допустимых значений для аргумента размер – от 1 до бесконечности со знаком плюс.