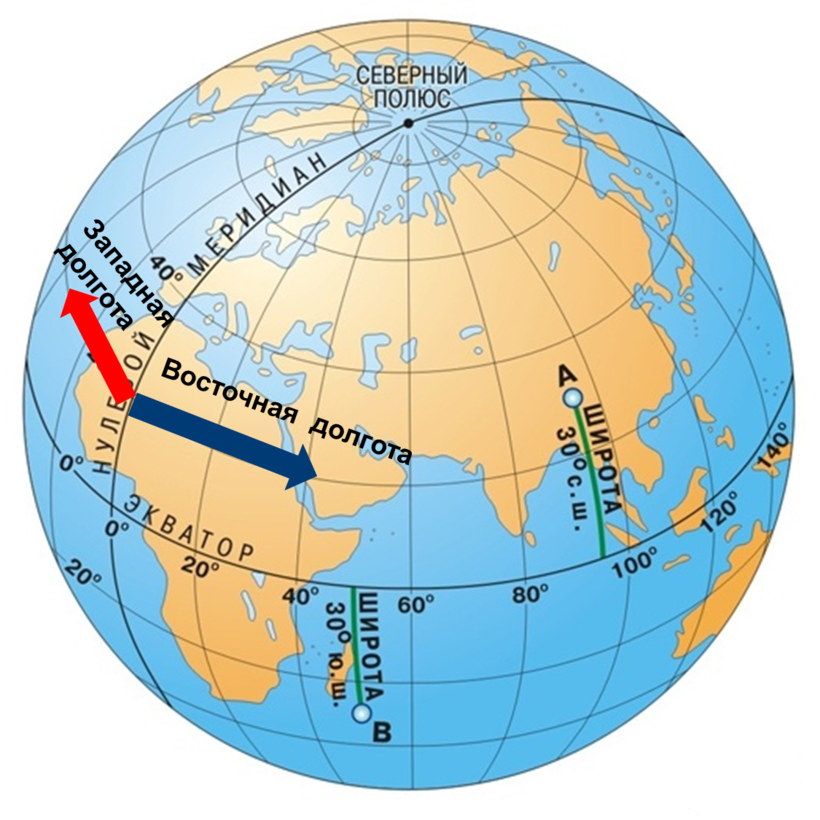
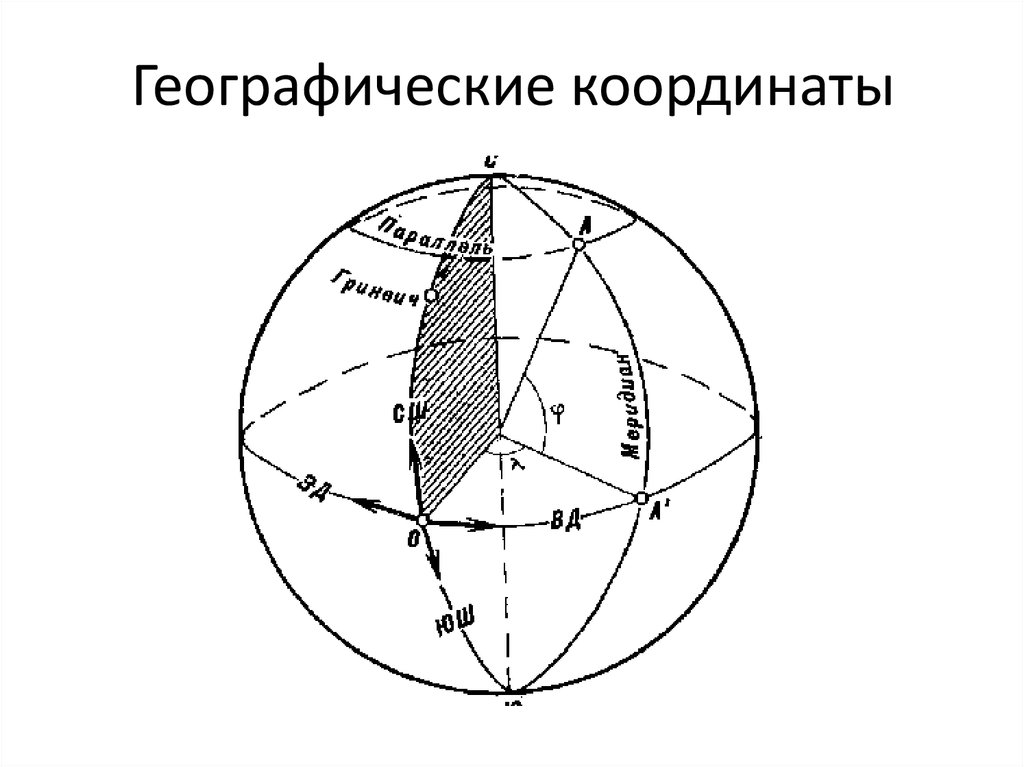
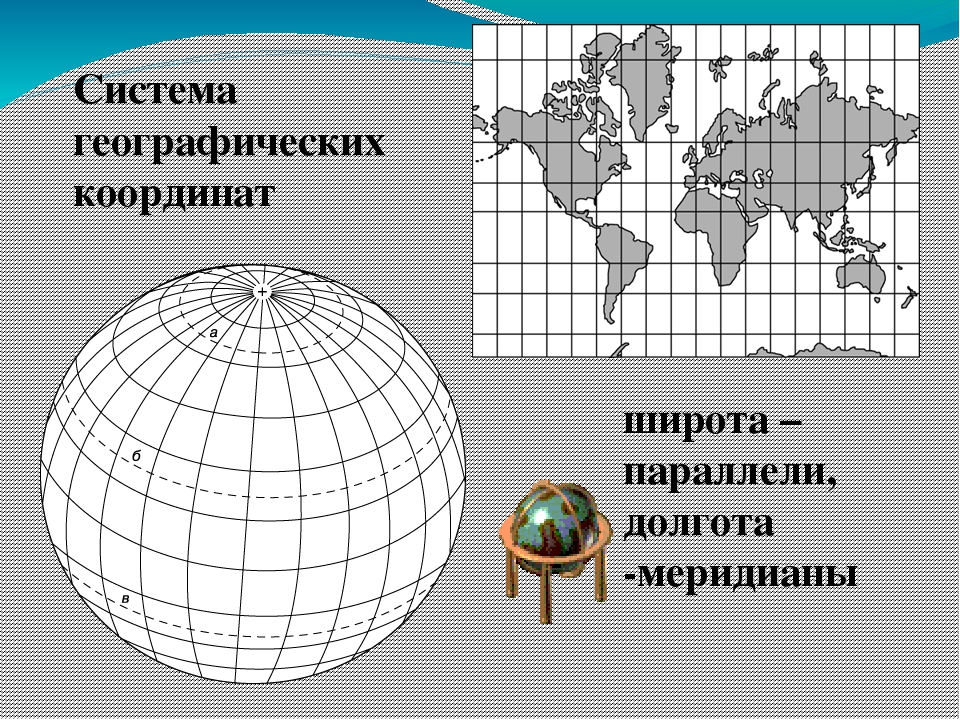
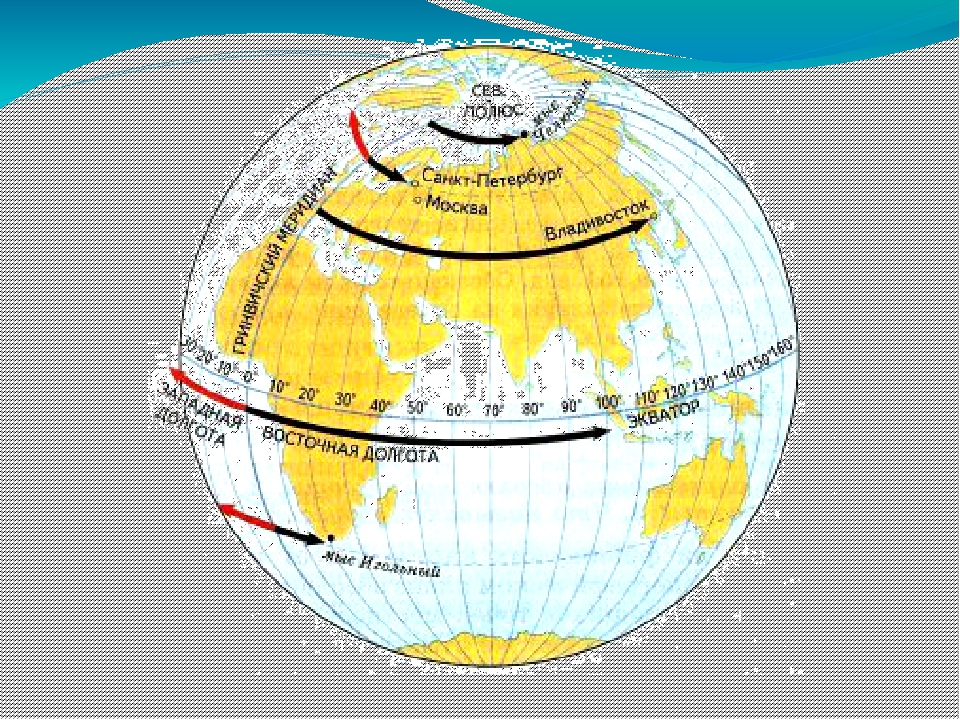
Меридиан — линия долготы
Для вычисления координат любой точки на земле, нужно знать его положение не только относительно севера и юга (это линии широты), но и относительно запада-востока. За это отвечают линии долготы. А так как западного и восточного полюса не существует, решили за начало отсчёта сделать линию нулевой долготы (или нулевой меридиан), проходящую через Гринвичскую лабораторию (Англия). Его принято называть — Гринвич. Линии долготы, названные меридианами, смыкаются на Северном полюсе и Южном полюсе. Область к востоку от Гринвича называется восточной долготой, а к западу, соответственно, западной. Любая точка на меридиане будет иметь одинаковую долготу, но разную широту.
Где я? Географические координаты
Легко объяснить, что стоишь слева от «той булочной за пятым домом» или на N-ской станции в центре зала. Но если речь идет о действительно больших расстояниях, нужно придумывать что-то другое.
Так появились географические координаты. Они, конечно, не сразу появились. Сначала надо было понять, что Земля шарообразная, потом немножко поколдовать над математикой, договориться, что координаты будут измеряться вот так…
История долгая, но в итоге появилось понятие географических координат: долготы и широты. С их помощью можно ориентироваться не только в родном районе, но и в пределах всей планеты.
Отвечая на вопрос из заголовка: я в Москве. Ее примерные координаты: 55° с. ш. и 37° в. д.
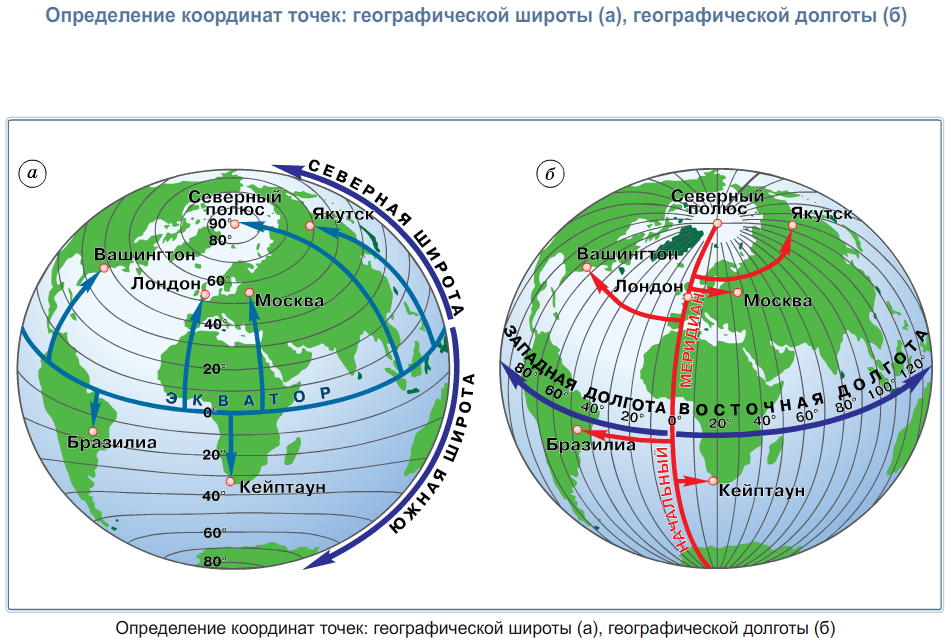
О понятии географической долготы
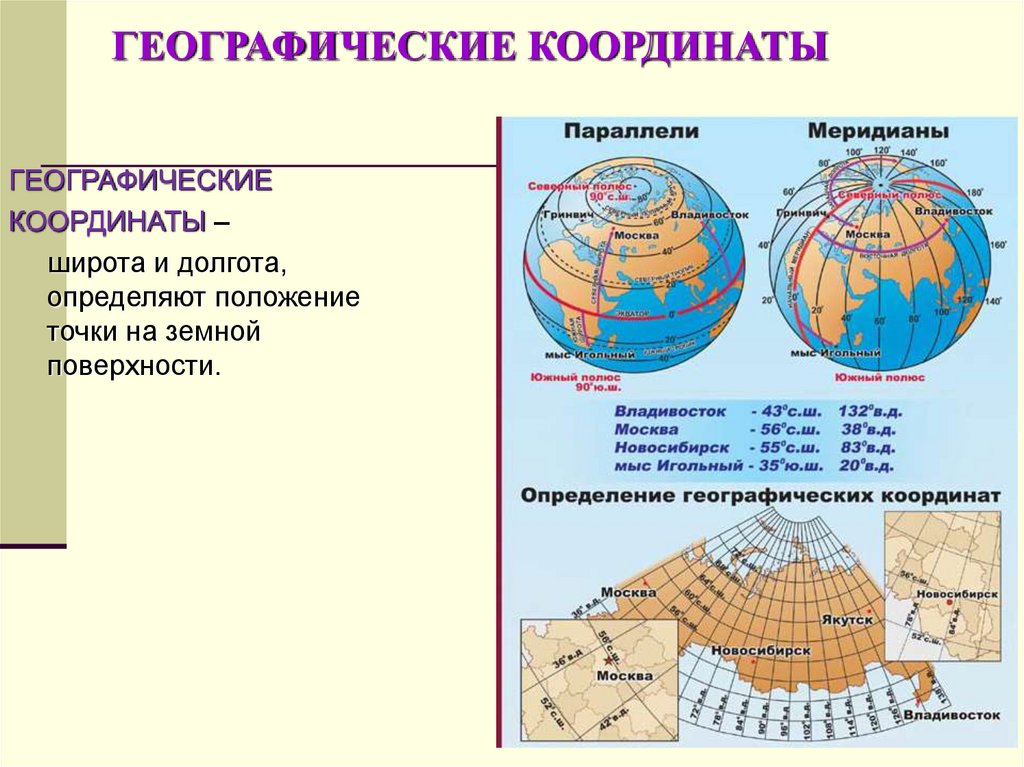
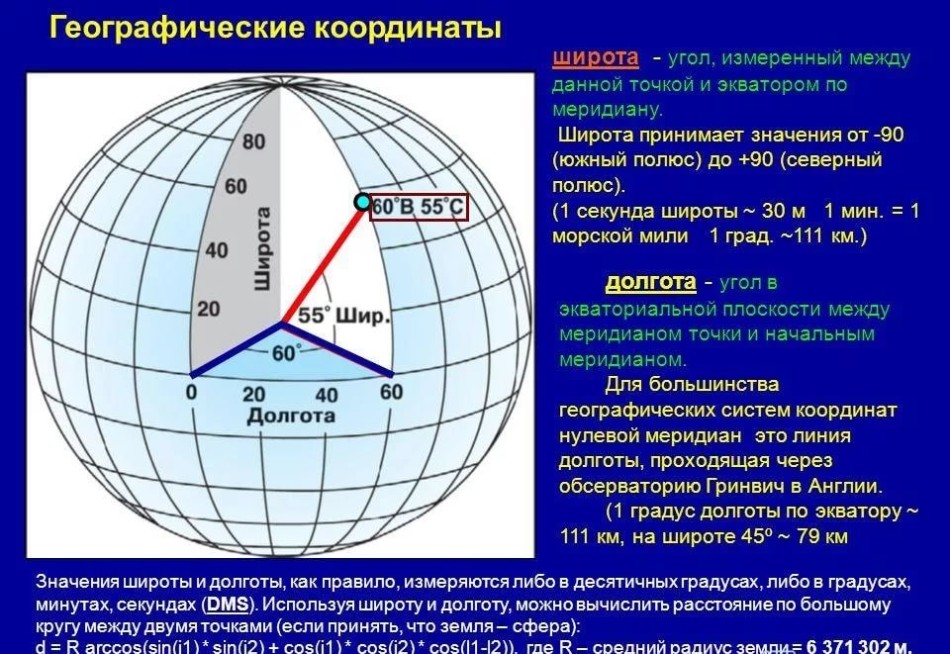
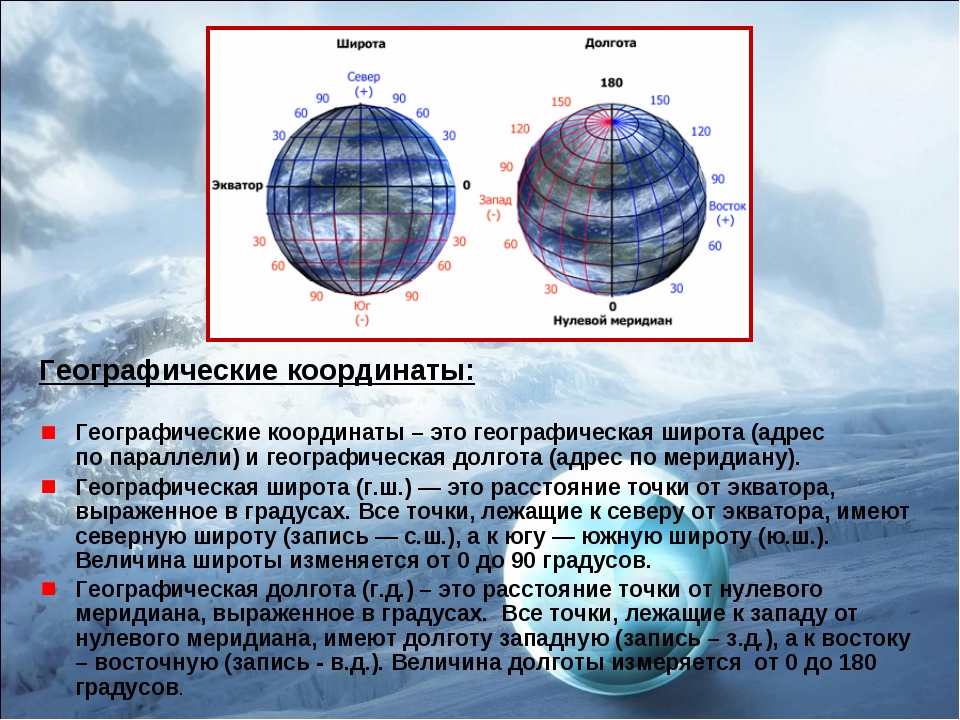
Любая точка на земном шаре имеет свои координаты, подобно адресу дома в черте города. По этому «адресу» можно найти какой-либо объект, а также нанести его на карту или глобус. Координаты — это одно из самых главных преимуществ и достоинств карт, хотя в детстве я его не оценила. Географические координаты составляют долгота и широта, то есть угловые величины, определяющие положение любой заданной точки на планете по отношению к экватору или нулевому меридиану. Таким образом, угол между плоскостью меридиана, идущего через обозначенную точку на Земле, и плоскостью Гринвичского меридиана — это и есть географическая долгота. Кстати, на других небесных телах используется такой же принцип определения координат точки, как и на Земле.
История происхождения термина «долгота»
Итак, почему географическую долготу называют долготой, несмотря на то, что Земля по форме напоминает шар? Название этому положил Гекатей Милетский, он жил в VI в. до н.э. Он составил карту, на которой наша планета была в форме овала, а не шара. Из-за этого недоразумения появилось понятие долготы.
В IV в. до н. э. Пифей из Массалии (так назывался раньше город Марсель) — отважный мореход однажды задумался, как определить положение судна в море, ведь на море не у кого спросить дорогу. И догадался, в полдень, когда Солнце было в зените, он мысленно провел линию между высотой Солнца в Массалии, самим городом и линией экватора — получился угол, измерив величину которого, он получил широту города Массалия, то есть его расположение относительно экватора. Таким образом Пифей определил широту родного города. Что интересно, у него получилось 43°12′, а в действительности широта Марселя составляет 43°17′. Но знать лишь широту было недостаточно, не доставало другой величины для точного определения положения.
Эту самую недостающую величину придумал Гиппарх Никкейский — астроном, живший на одно столетие позже Пифея. Он научился определять широту по звездам и долготу по лунным затмениям.
Таким образом, географическая долгота — это угол, отсчитываемый от нулевого меридиана до заданного объекта, выраженное в градусах от 0° до 180°
Долгота на других небесных телах
Системы координат на поверхности других небесных тел определяются по аналогии с Землёй, при этом расположение координатной сетки может варьироваться в зависимости от расположения оси вращения и других характеристик соответствующего небесного тела. Для небесных тел с наблюдаемыми жёсткими поверхностями (планет) координатные сетки привязаны к каким-либо элементам поверхности, например кратерам. Условный северный полюс планеты — это тот полюс вращения, который лежит на северной стороне плоскости эклиптики. Расположение нулевого (опорного) меридиана, а также положение северного полюса планеты может изменяться со временем из-за прецессии оси вращения этой планеты (или спутника). Если угол положения опорного меридиана планеты увеличивается со временем, планета имеет прямое вращение; в противном случае вращение называется ретроградным.
При отсутствии другой информации ось вращения планеты считается перпендикулярной к средней плоскости её орбиты; Меркурий и большинство спутников планет находятся в этой категории. Для многих спутников предполагается, что период вращения вокруг своей оси равен периоду обращения вокруг своей планеты. В случае планет-гигантов, поскольку объекты на их поверхностях постоянно меняются и движутся с различными скоростями, используется период вращения их магнитных полей. В случае с Солнцем этот критерий не выполняется (поскольку магнитосфера Солнца очень сложна и не имеет устойчивого вращения), и вместо этого используется значение для скорости вращения солнечного экватора.
При оценке планетографических долгот, по аналогии с Землёй, используются термины «западные долготы» и «восточные долготы» (то есть, долготы, увеличивающиеся в сторону условного востока). При этом планетоцентрическая долгота всегда измеряется положительно на восток, независимо от того, в каком направлении вращается планета. Восток определяется как направление против часовой стрелки, если смотреть на планету сверху со стороны её северного полюса — того, который в наибольшей мере совпадает с северным полюсом Земли. Обозначения планетографических долгот, по аналогии с земными координатами, традиционно записывались с использованием букв «E» и «W» вместо «+» или «−». Например, −91°, 91° W, +269° и 269° E означают одно и то же.
Опорные поверхности для некоторых планет (таких, как Земля и Марс) представляют собой эллипсоиды вращения, для которых экваториальный радиус больше полярного, то есть являются сплюснутыми сфероидами. Меньшие объекты, такие как Ио, Мимас и т. д., как правило, лучше аппроксимируются трехосными эллипсоидами; однако, использование моделей трехосных эллипсоидов усложнило бы многие вычисления, особенно связанные с картографическими проекциями, поэтому в для этих целей в качестве эталонов чаще используются сферические модели.

Опорный меридиан Марса проходит через кратер Эйри-0
Для разработки стандарта для карт Марса примерно с 2002 года в качестве нулевого меридиана выбран меридиан, расположенный у кратера Эйри-0. Для другой планеты с твердой поверхностью, наблюдаемой с Земли — Меркурия — используется термоцентрическая координата: опорный меридиан проходит через точку на экваторе, где отмечена максимальная температура на планете (при этом Солнце кратковременно совершает ретроградное движение в меркурианский полдень во время перигелия). По соглашению, этот меридиан определён точно как 20° долготы к востоку от кратера .
Синхронно вращающиеся небесные тела имеют «естественный» опорный меридиан, проходящий через точку, ближайшую к большему небесному телу: 0° — центр первичного полушария, 90° — центр ведущего полушария, 180° — центр противоположному первичному полушария, и 270° — центр заднего полушария. Однако по причине эллиптических форм планетных орбит и наклона оси вращения планет эта точка на небосводе небесного тела превращается в аналемму.
Длина градуса долготы
Длина градуса долготы на определённой широте зависит только от расстояния от центра Земли до соответствующей параллели. Если форму Земли считать сферической с радиусом a, то длина дуги в один градус долготы (восток-запад) на параллели широты φ будет равна
- Δlong1=π180∘acosϕ{\displaystyle \Delta _{\rm {long}}^{1}={\frac {\pi }{180^{\circ }}}a\cos \phi }.
| φ | Δ1lat | Δ1long |
|---|---|---|
| 0° | 110.574 km | 111.320 km |
| 15° | 110.649 km | 107.551 km |
| 30° | 110.852 km | 96.486 km |
| 45° | 111.133 km | 78.847 km |
| 60° | 111.412 km | 55.800 km |
| 75° | 111.618 km | 28.902 km |
| 90° | 111.694 km | 0.000 km |
Если же форму Земли принять за эллипсоид, длина дуги градуса долготы вычисляется
- Δlong1=πacosϕ180∘1−e2sin2ϕ{\displaystyle \Delta _{\rm {long}}^{1}={\frac {\pi a\cos \phi }{180^{\circ }{\sqrt {1-e^{2}\sin ^{2}\phi }}}}}
где эксцентриситет эллипсоида e рассчитывается как соотношение между его большой (a) и малой (b) полуосью (соответственно, экваториальным и полярным радиусами Земли)
- e2=a2−b2a2{\displaystyle e^{2}={\frac {a^{2}-b^{2}}{a^{2}}}}.
Альтернативная формула:
- Δlong1=π180∘acosψгдеtanψ=batanϕ{\displaystyle \Delta _{\rm {long}}^{1}={\frac {\pi }{180^{\circ }}}a\cos \psi \quad {\mbox{где}}\tan \psi ={\frac {b}{a}}\tan \phi }.
Значение сos φ уменьшается от 1 на экваторе до 0 на полюсах; это означает, что параллели «сжимаются» от экватора до точки на полюсах, поэтому длина градуса долготы также уменьшается. Это контрастирует с небольшим (1 %) увеличением от экватора к полюсу. Таблица показывает данные для эллипсоида, применяемого в системе координат WGS84, где а = 6378137,0 м, и b = 6356752,3142 м. Необходимо отметить, что расстояние между двумя точками на расстоянии 1 градуса на одном и том же круге широты, измеренное вдоль этого круга широты, будет немного больше, чем самое короткое расстояние (геодезическая) между этими точками (за исключением экватора, где эти величины равны); разница составляет менее 0,6 м.
Географическая миля определяется как длина одной минуты дуги вдоль экватора, поэтому длина градуса долготы вдоль экватора составляет ровно 60 географических миль или 111,3 километра. Протяжённость 1 минуты долготы вдоль экватора составляет 1 географическую милю, или 1,855 км, а длина 1 секунды долготы вдоль экватора составляет 0,016 географической мили, или 30,916 м.
История вычисления географической долготы
До начала эры Великих географических открытий мореплаватели ориентировались по положению Полярной звезды в небе (определяли только широту).
С открытием Нового Света вопрос о вычислении долготы стал стоять более остро. Галилей и Вернер успели предложить свои методы её определения. Их способы основывались на измерении положения небесных тел.
Недостатки этих методов:
- необходимость в сложном астрономическом оборудовании;
- трудность вычислений;
- высокий риск получения неверных результатов.
Был более простой способ: сравнение местного времени порта отправления со временем в точке пребывания. Для реализации метода нужно было создать высокоточные часы, а в XVI веке ультраточными считались часы с секундной стрелкой.
В 1749 году Джоном Гаррисоном были созданы такие часы.
Высота
Основная статья: Высота над уровнем моря
Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота.
Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.
В пределах географической оболочки применяется обычно высота над уровнем моря, отсчитываемая от уровня «сглаженной» поверхности — геоида.
Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений.
Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.
Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако ‘не’ служит координатой.
Что такое долгота и как ее найти
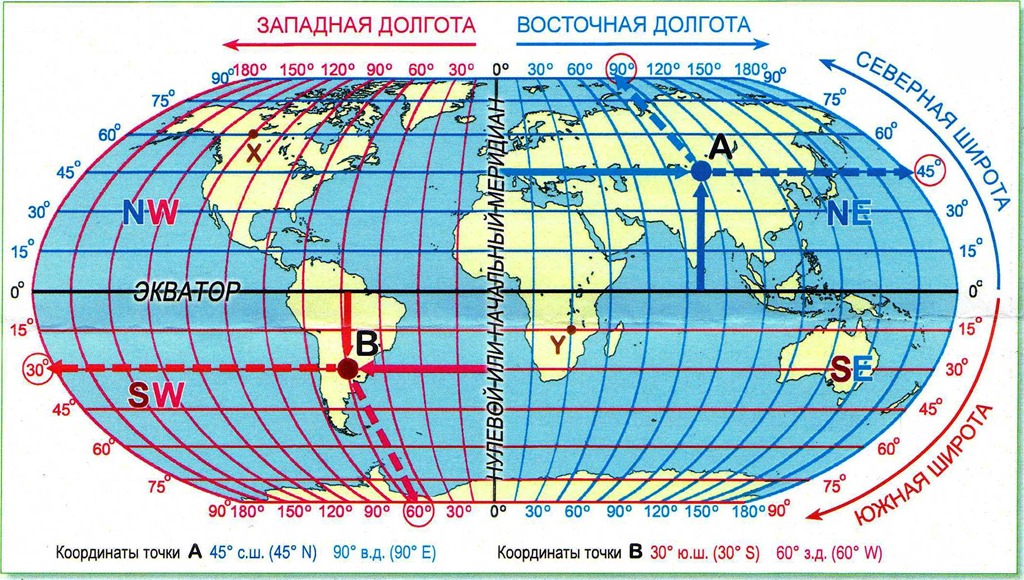
Долгота — это величина, на которую удалено положение заданной местности относительно Гринвича, то есть нулевого меридиана.
Линии долготы
Долготе аналогично присуще измерение в угловых единицах, только с 0° до 180° и с приставкой — восточная либо западная.
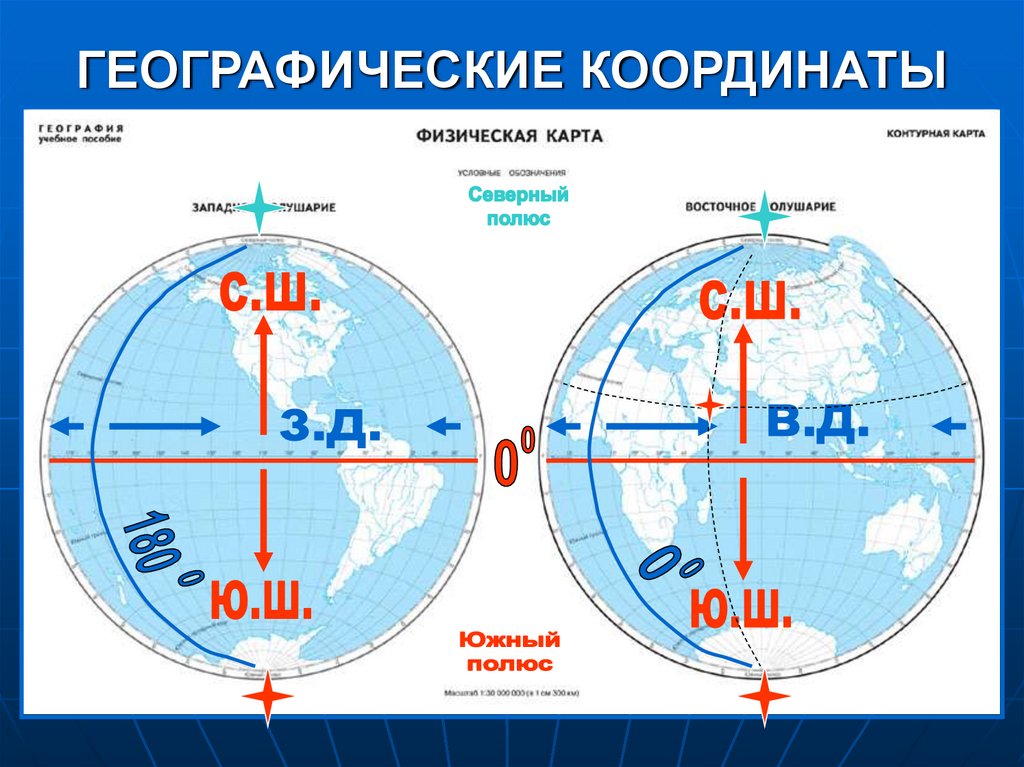
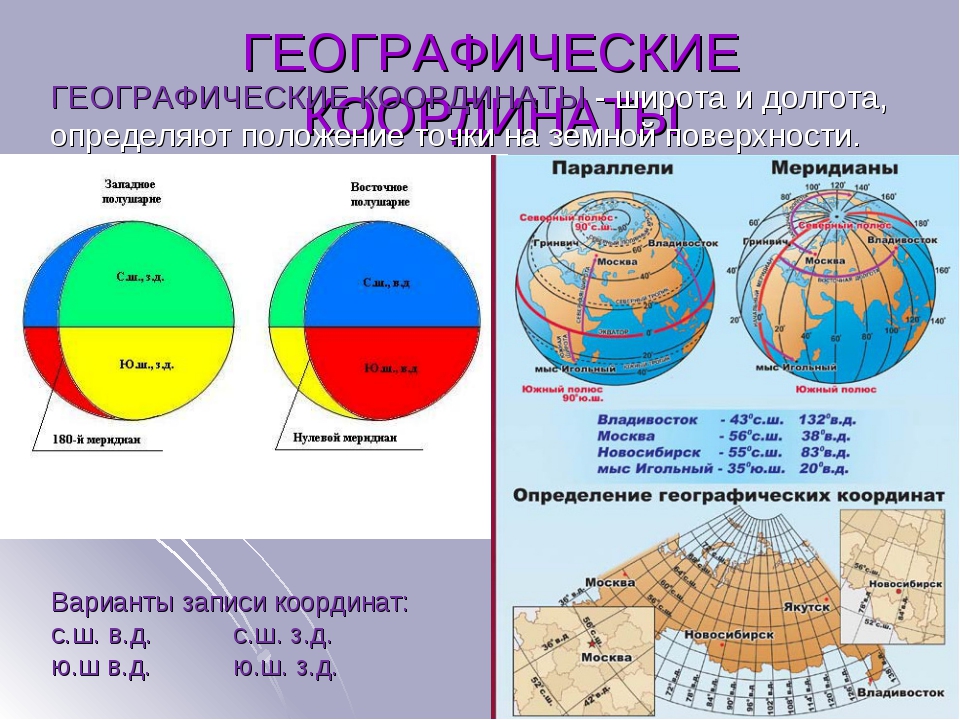
- Нулевой меридиан Гринвича вертикально опоясывает шар Земли, проходя через оба полюса, разделяя его на западное и восточное полушария.
- Каждая из частей, находящихся к западу от Гринвича (в западном полушарии) , будет носить обозначение западной долготы (з.п.).
- Каждая из частей, удаленная от Гринвича на восток и расположенная в восточном полушарии, будет носить обозначение восточной долготы (в.п.).
- Нахождение каждой точки по одному меридиану имеют единую долготу, но различную широту.
- Меридианы нанесены на карты в виде вертикальных полос, изогнутых в форме дуги. Чем мельче масштаб карты, тем прямее будет полоса меридиана.
Запись и исчисление долготы
См. также: Универсальное время и Уравнение времени
Долгота указывается как угловая величина в диапазоне от 0° (значение на нулевом меридиане) до +180° на востоке и −180° на западе. Греческая буква λ (лямбда), используется для обозначения местоположения места на Земле к востоку или западу от нулевого меридиана.
Каждый градус долготы делится на 60 минут, каждая из которых делится на 60 секунд. Таким образом, долгота указывается в шестидесятеричной системе счисления например, как 23°27′30″ в. д. Для более высокой точности указываются доли угловых секунд. Альтернативное представление использует запись значения долготы в градусах и минутах, где доли минуты выражаются десятичной дробью, например: 23°27,5′ E. Градусы также могут быть выражены в виде десятичной дроби, например: 23,45833° E. Для расчётов угловая мера может быть преобразован в радианы, поэтому долгота также может быть выражена таким образом как дробная часть π.
При расчётах буквенные индексы E и W заменяются знаками «+» (обычно опускается) и «−», если речь идёт о Западном полушарии. Положительные значения долготы в Восточном полушарии обусловлены использованием правосторонней системы декартовых координат с Северным полюсом наверху. Наряду с вышеуказанной системой отсчёта отрицательных значений долготы, изредка (главным образом в США), иногда используется и система, в которой отрицательные значения принимают долготы Восточного полушария; согласно оценке (подразделение NOAA) такой подход более удобен при
обработке координат объектов Западного полушария.
Меридианы со значениями долготы, кратными 15°, без параллелей, за исключением экватора
Не существует способов, позволяющих определить долготу точки земной поверхности напрямую, это можно сделать только с использованием учёта времени. Долгота в данной точке может быть определена путём расчета разницы между местным солнечным временем её местоположения и всемирным координированным временем (UTC). Поскольку в сутках 24 часа, а полный круг содержит 360 градусов, солнце движется по небу с угловой скоростью 15° в час. Таким образом, для выполнения точного расчёта долготы местности необходимо установить хронометр (часы) на UTC и определить местное время с помощью солнечного или астрономического наблюдения.
Сингулярность и разрыв долготы
На географических полюсах Земли значения долготы становятся сингулярными, поэтому расчёты, достаточно точные для других местностей, могут оказаться неточными на полюсах или рядом с ними.
История измерения долготы
Основная статья: История измерения долготы
Способ измерения долготы Америго Веспуччи
Измерение долготы является чрезвычайно важным для картографии и навигации. Определение широты достаточно успешно осуществлялось моряками и путешественниками путём наблюдения с помощью квадранта или астролябии высоты Солнца или нанесённых на карту звёзд. Определение же долготы оказалось куда более сложным, на протяжении веков над ним трудились величайшие научные умы.
Одним из первых способ определения долготы предложил известный путешественник Америго Веспуччи, посвятивший много времени и сил изучению проблемы во время своего пребывания в Новом Свете:
Наряду с методом Веспуччи, было предложено ещё несколько астрономических методов измерения долготы — Иоганна Вернера (, 1514 год), Галилео Галилея (по положению спутников Юпитера, 1612 год), — но для их реализации требовались сложные астрономические инструменты и вычисления. Более простой способ, изобретение которого приписывают Фризиусу Гемме — сравнение местного солнечного времени с точным в референсной точке (порту) — требовал очень точных часов.
В 1714 году британский парламент предложил огромную премию за разработку метода определения долготы — £10 000 за метод определения долготы с погрешностью в пределах одного градуса большого круга Земли, то есть в пределах 60 морских миль, £15 000, если погрешность будет менее двух третей этого расстояния, £20 000, если она будет менее половины этого расстояния. Для определения долготы с такой погрешностью во время плавания в Вест-Индию требовались часы со среднесуточным уходом не более 3 секунд (при том, что часы в то время считались очень точными, если вообще имели минутную стрелку).
Джон Гаррисон, успешно решивший проблему
Плотник и часовщик-самоучка Джон Гаррисон в 1749 году изготовил часы, которые были более точными на море, чем любые другие на суше: среднесуточный уход составлял менее 2 секунд, и после 45 дней плавания погрешность определения долготы составила 10 миль. Однако парламент к тому времени изменил условия конкурса — теперь требовалась не только точность, но и компактность часов. В ответ Гаррисон в 1760 году представил новую модель диаметром 12 см. Эти часы были проверены во время двух плаваний в Вест-Индию — в 1761 и 1764 годах, уход при этом составил 5 секунд за три месяца путешествия. В марте 1776 года ему выплатили премию.
Часы-хронометр были дороги, и на практике всё же обычно долгое время применялся метод лунных расстояний с использованием таблиц, публикуемых в «Морском альманахе», который с 1766 года издавал Невил Маскелайн.
Настоящую революцию в определении долготы произвело изобретение радио в конце XIX века. Теперь сигналы точного времени из пункта с известной долготой можно было принять в любой точке Земли. Затем появилась радионавигация. В настоящее время для определения координат для целей навигации применяются спутниковые системы навигации.
Долгота: линии, углы, градусы
Хорошая новость — для вычисления географической долготы Землю принимают за шар (сферу). Все просто и ясно:
- меридианы;
- прямые линии;
- углы.
Меридианы — линии, которые тянутся по поверхности Земли от одного полюса к другому и делают Землю похожей на арбуз. Меридианы — изогнутые линии. Но спокойно! Вычислять длину меридиана не придется.
Берем Гринвичский меридиан, он же нулевой, потом берем точку, долготу которой хотим узнать, представляем, что от этих точек отходят плоскости, пересекающиеся в центре Земли. Угол между этими плоскостями и будет долготой.Восточную долготу отсчитывают к востоку от нулевого меридиана, западную — к западу.
Откуда ведется отсчет долготы
Отсчет долготы ведется от начального (другими словами — нулевого) меридиана. В качестве начального меридиана на Земле принят меридиан, проходящий через известную обсерваторию в Великобритании (в Гринвиче). От него начинают отсчитывать долготу в обе стороны. При отсчете от 0° до 180° к востоку принято говорить: столько-то градусов восточной долготы, а при отсчете на запад — западной долготы.
Отмечу, что по сей день существуют еще топографические карты, на которых можно встретить местные нулевые меридианы, проходящие через:
- Мадрид (Испания);
- Рим (Италия)
- Париж (Франция);
- Копенгаген (Дания);
- Кадис (Испания).
В России продолжительное время за начальный считался Пулковский меридиан.
Движение литосферных плит и долгота
Литосферные плиты Земли движутся относительно друг друга в разных направлениях со скоростью порядка 50—100 мм в год. Таким образом, точки на поверхности Земли, лежащие на разных плитах, всегда находятся в движении относительно друг друга. Например, разница в долготе между точкой, расположенной на экваторе в Уганде на Африканской плите и точкой на экваторе в Эквадоре на Южно-Американской плите увеличивается примерно на 0,0014 угловых секунд в год. Эти тектонические движения также влияют на широту точек земной поверхности.
При использовании какой-либо глобальной системы координат (например, WGS 84), долгота места на поверхности будет меняться из года в год. Чтобы минимизировать это изменение, при работе с точками на одной литосферной плите можно использовать другую систему отсчёта, координаты которой зафиксированы на конкретной плите, например, NAD83 для Северной Америки или ETRS89 для Европы.