Примечания
- ↑ , с. 264—266, 534—536.
- . // Website Online Etymology Dictionary. Дата обращения 7 февраля 2016.
- , с. 67.
- Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
- . // Website Jeff Miller Web Pages. Дата обращения 7 февраля 2016.
- , с. 30.
- Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- , Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
- ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.
Примечания
- Гутников В. С. . Интегральная электроника в измерительных приборах. — Л.: Энергия, 1974. — 144 с. — С. 14—16.
- , с. 534.
- Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 320, 349, 352, 368.
- . // Website Jeff Miller Web Pages. Дата обращения 5 февраля 2016.
- , с. 149—150.
- , с. 30.
- Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- Эллис М., Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
Связь с естественным языком
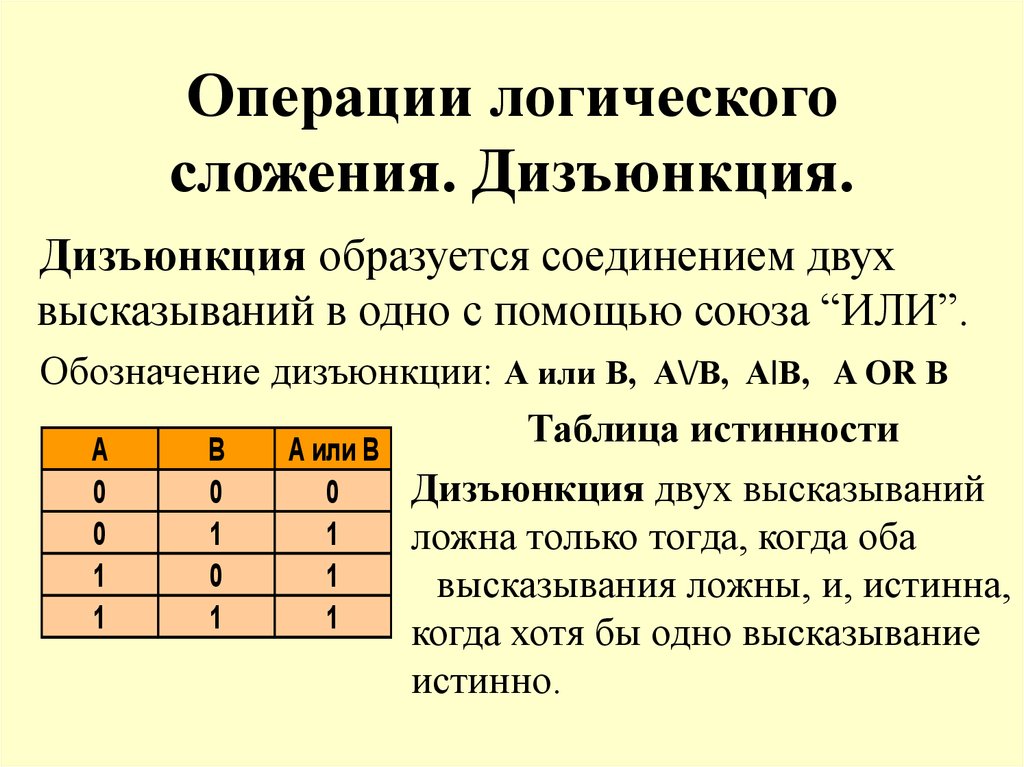
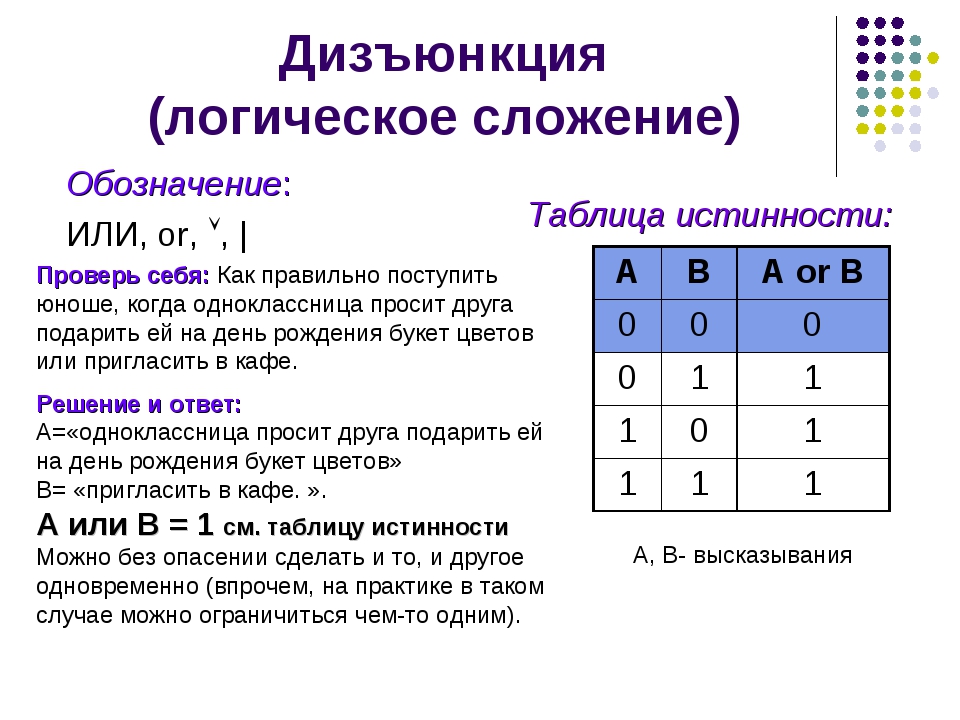
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и (или)», иногда «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}.
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — строгой дизъюнкции (исключающего «ИЛИ»).
Обозначения
Наиболее часто встречаются следующие обозначения для операции конъюнкции:
a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}
(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: ab{\displaystyle ab}).
При этом обозначение a∧b{\displaystyle a\land b}, рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия). Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930).
Обозначение для конъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой конъюнкции и для логической конъюнкции).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(modk){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел).
А где же побитовое исключающее ИЛИ (XOR)?
Побитовое исключающее ИЛИ (XOR) — это логический оператор, который используется в некоторых языках программирования для проверки на истинность нечётного количества условий.
| Побитовое исключающее ИЛИ (XOR) | ||
| Левый операнд | Правый операнд | Результат |
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | false |
В языке C++ нет такого оператора. В отличии от логических И/ИЛИ, к XOR не применяется короткий цикл вычислений. Однако его легко можно сымитировать, используя оператор неравенства ():
if (a != b) … // a XOR b (предполагается, что a и b имеют тип bool)
| 1 | if(a!=b)…// a XOR b (предполагается, что a и b имеют тип bool) |
Можно также расширить количество операндов:
if (a != b != c != d) … // a XOR b XOR c XOR d (предполагается, что a, b, c и d имеют тип bool)
| 1 | if(a!=b!=c!=d)…// a XOR b XOR c XOR d (предполагается, что a, b, c и d имеют тип bool) |
Следует отметить, что вышеприведенные шаблоны XOR работают только, если операнды имеют логический (а не целочисленный) тип данных. Если вы хотите, чтобы это работало и с целыми числами, то используйте .
Форма XOR, которая работает и с другими типами данных (с помощью оператор static_cast мы можем конвертировать любой тип данных в bool):
if (static_cast<bool>(a) != static_cast<bool>(b) != static_cast<bool>(c) != static_cast<bool>(d)) … // a XOR b XOR c XOR d, для любого типа, который может быть конвертирован в bool
| 1 | if(static_cast<bool>(a)!=static_cast<bool>(b)!=static_cast<bool>(c)!=static_cast<bool>(d))…// a XOR b XOR c XOR d, для любого типа, который может быть конвертирован в bool |
Обозначения
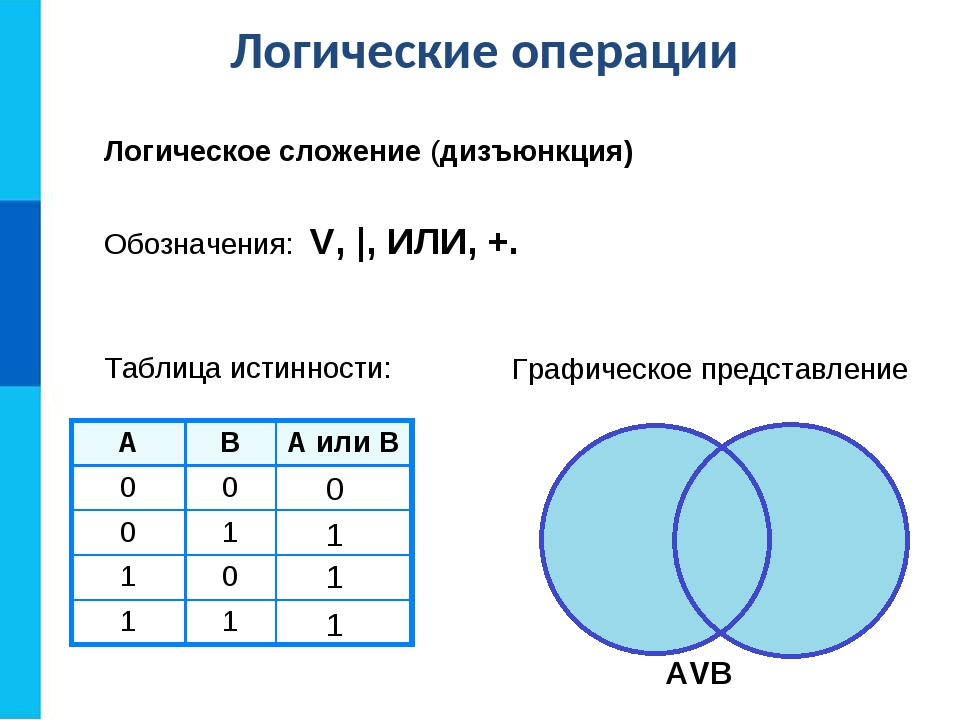
Наиболее часто встречаются следующие обозначения для операции дизъюнкции:
- a∨b,a{\displaystyle a\lor b,\;a} || b,a{\displaystyle b,\;a} | b,a ORb{\displaystyle b,\;a~{\mbox{OR}}\,\,b},max(a,b).{\displaystyle ,\;\max(a,b).}
При этом обозначение a∨b{\displaystyle a\lor b}, рекомендованное международным стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике. Появилось оно не сразу: Джордж Буль, положивший начало систематическому применению символического метода к логике, не работал с дизъюнкцией (используя вместо неё строгую дизъюнкцию, которую обозначал знаком +), а Уильям Джевонс предложил для дизъюнкции знак . Эрнст Шрёдер и П. С. Порецкий вновь использовали знак +, но уже применительно к обычной дизъюнкции. Символ ∨{\displaystyle \lor } как обозначение дизъюнкции впервые встречается в статье «Математическая логика, основанная на теории типов»Бертрана Рассела (1908); он образован от лат. vel, что означает «или».
Обозначение для дизъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для дизъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой дизъюнкции и для логической дизъюнкции).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∨b)=max(a,b).{\displaystyle (a\lor b)\,=\,\max(a,b).} Таким образом, дизъюнкция оказывается частным случаем операции вычисления максимума; это открывает наиболее естественный способ определить операцию дизъюнкции в системах многозначной логики.
Булева алгебра
Определение.
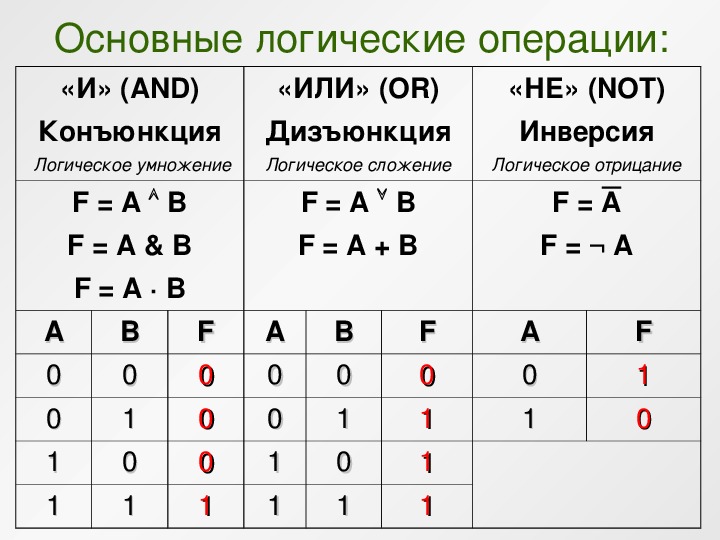
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).
Правило: результат равен наименьшему операнду.
Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений ,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, true>false{\displaystyle true>false}, при цифровом обозначении старшинство естественно 1>{\displaystyle 1>0}.
Правило: результат равен 1{\displaystyle 1}, если все операнды равны 1{\displaystyle 1}; во всех остальных случаях результат равен {\displaystyle 0}.
Таблицы истинности:
для бинарной конъюнкции
| a{\displaystyle a} | b{\displaystyle b} | a∧b{\displaystyle a\land b} |
|---|---|---|
| {\displaystyle 0} | {\displaystyle 0} | {\displaystyle 0} |
| 1{\displaystyle 1} | {\displaystyle 0} | {\displaystyle 0} |
| {\displaystyle 0} | 1{\displaystyle 1} | {\displaystyle 0} |
| 1{\displaystyle 1} | 1{\displaystyle 1} | 1{\displaystyle 1} |
для тернарной конъюнкции
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a∧b∧c{\displaystyle a\land b\land c} |
|---|---|---|---|
| 1 | |||
| 1 | |||
| 1 | 1 | ||
| 1 | |||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | 1 | 1 |
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции.
Информация в информатике
Понятие данного термина в информатике имеет целый ряд свойств. К таким свойствам относятся следующие:
- Достоверность,
- Релевантность,
- Полнота,
- Эргономичность,
- Актуальность,
- Защищённость,
- Доступность.
Информация является особым видом ресурсов, который обладает свойствами, характерными именно для него. К таким свойствам относятся следующие:
- Стираемость,
- Запоминаемость,
- Преобразуемость,
- Передаваемость,
- Воспроизводимость.
Рассмотрим каждое из данных свойств более подробно.
- Запоминаемость является одним из самых главных свойств данных. Запоминаемую информацию принято называть макроскопической. При этом имеются в виду пространственные масштабы запоминающей ячейки, а также время запоминания. С макроскопическими данными люди имеют дело на реальной практике.
- Передача происходит с помощью специальных каналов связи, в том числе и с помехами. Передаваемость хорошо исследована на основе теории Шеннона. В этом случае имеется в виду немного другой аспект, заключающийся в способности сведений к их копированию, таким образом, она может быть запоминающейся другой макроскопической системой, одновременно с этим оставаясь тождественной самой себе. Становится очевидным, что при копировании количество данных не будет возрастать.
- Говоря о воспроизводимости сведений, необходимо отметить, что она тесно связывается с ее передаваемостью, но не относится к ее независимому базовому свойству. Если же под передаваемостью имеется в виду, что не стоит считать существенными пространственные отношения между отдельными частями системы, среди которых передаются данные, то воспроизводимость характеризуется неиссякаемостью и неистощаемостью сведений, то есть во время копирования сведений будет оставаться тождественной самой себе.
- Преобразуемостью называется фундаментальное свойство данных. Она подразумевает то, что сведения могут сами поменять форму и способ своего существования. Копируемость при этом является разновидностью преобразования сведений, но ее количество при этом не меняется. Говоря об общем случае, стоит отметить, что количество данных в процессе преобразования будет меняться, но не будет возрастать.
- Стираемость тоже относится к независимому свойству сведений. Стираемость связана с таким преобразованием данных, во время которого ее количество снижается или становится равным нулю.
Программирование
В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++/Perl/PHP логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|». В языках Pascal/Delphi оба вида дизъюнкции обозначаются с использованием ключевого слова «or», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.
Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:
if (a || b)
{
/* какие-то действия */
};
Результат будет равен false{\displaystyle false}, если оба операнда равны false{\displaystyle false} или {\displaystyle 0}. В любом другом случае результат будет равен true{\displaystyle true}.
При этом применяется стандартное соглашение: если значение левого операнда равно true{\displaystyle true}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
{$B-}
или выключающую
{$B+}
подобное поведение. Например, если левый операнд проверяет необходимость вычисления правого операнда:
if (a == NULL || a->x == )
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдёт разыменования нулевого указателя.
Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 011001012{\displaystyle 01100101_{2}} |
| b = | 001010012{\displaystyle 00101001_{2}} |
| то | |
| a ИЛИ b = | 011011012{\displaystyle 01101101_{2}} |
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:
- a→a∨b{\displaystyle a\to a\lor b}
- b→a∨b{\displaystyle b\to a\lor b}
- (a→c)→((b→c)→((a∨b)→c)){\displaystyle (a\to c)\to ((b\to c)\to ((a\lor b)\to c))}
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции
Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Программирование
В языках C/C++, Java, C#, Ruby, PHP, JavaScript, Python и т. д. битовая операция поразрядного дополнения обозначается символом «^», в языках Паскаль, Delphi, Ada, Visual Basic — зарезервированным словом xor, в языке ассемблера — одноимённой логической командой. При этом сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
- если
a=011001012{\displaystyle a=01100101_{2}}
b=001010012{\displaystyle b=00101001_{2}}
- то
a ^b=010011002{\displaystyle a{\hat {\ }}b=01001100_{2}}
Выполнение операции исключающее «или» для значений логического типа (true, false) производится в разных языках программирования по-разному. Например, в Delphi используется встроенный оператор XOR (пример: условие1 xor условие2). В языке C, начиная со стандарта C99, оператор «^» над операндами логического типа возвращает результат применения логической операции XOR. В С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов производится его побитовое применение.
Использование побитового исключающего «или» позволяет поменять местами значения целых переменных без использования дополнительной памяти.
Примечания
- ↑ , с. 264—266, 534—536.
- , с. 67.
- Стяжкин Н. И. Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
- , с. 30.
- Пратт Т. Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- Эллис М., Строуструп Б. Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
- ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.
Связь с естественным языком
В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:
- «результат истинен (равен 1), если A не равно B (A≠B)»;
- «если A не равно B (A≠B), то истина (1)».
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
- A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
- A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).
Операция ⊕{\displaystyle \oplus }исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ».
Операция ∨{\displaystyle \lor }включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ».
Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
Обозначения
Запись может быть префиксной («польская запись») — знак операции ставится перед операндами, инфиксной — знак операции ставится между операндами и постфиксной — знак операции ставится после операндов. При числе операндов более 2 префиксная и постфиксная записи экономичнее инфиксной записи. Чаще всего встречаются следующие варианты записи:⊕2(a,b), a{\displaystyle \oplus _{2}(a,b),~a} ^ b, a⊕b,a⊕2b,a+2b,{\displaystyle b,~a\oplus b,a\oplus _{2}b,a+_{2}b,} a ≠ b, a≠b,(a,b)⊕2,a XOR b{\displaystyle a\neq b,(a,b)\oplus _{2},a~XOR~b}
В Юникоде есть символы для сложения по модулю 2: U+22BB ⊻ xor, U+2295 ⊕ circled plus и U+2A27 ⨧ plus sign with subscript two, U+2A52 ⩒ logical or with dot above, а также символ для суммы по модулю 2: U+2A0A ⨊ modulo two sum.
Булева алгебра
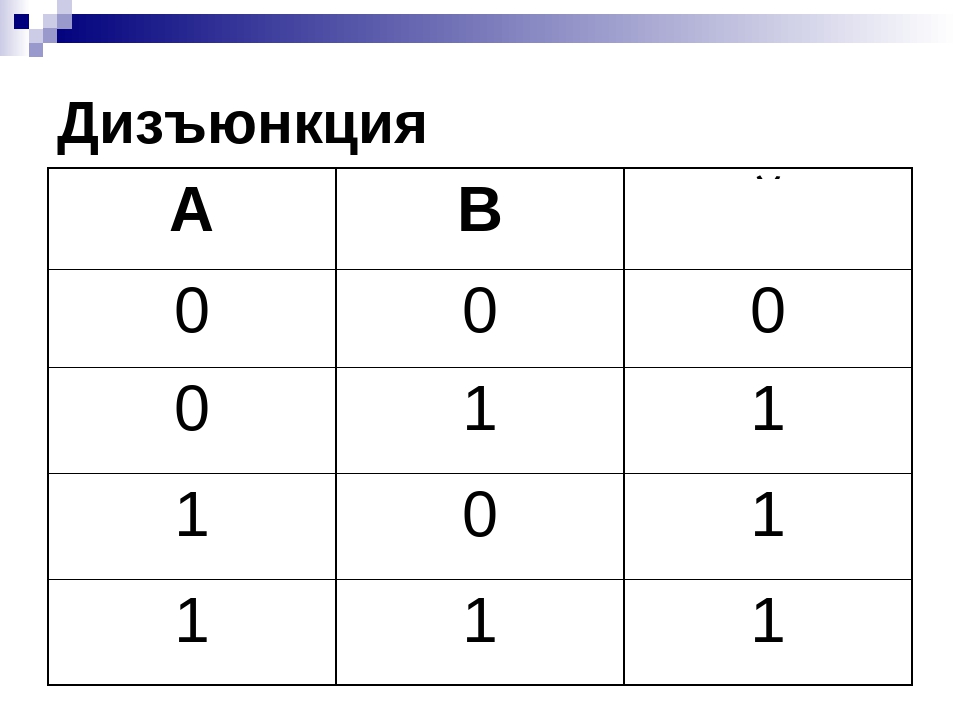
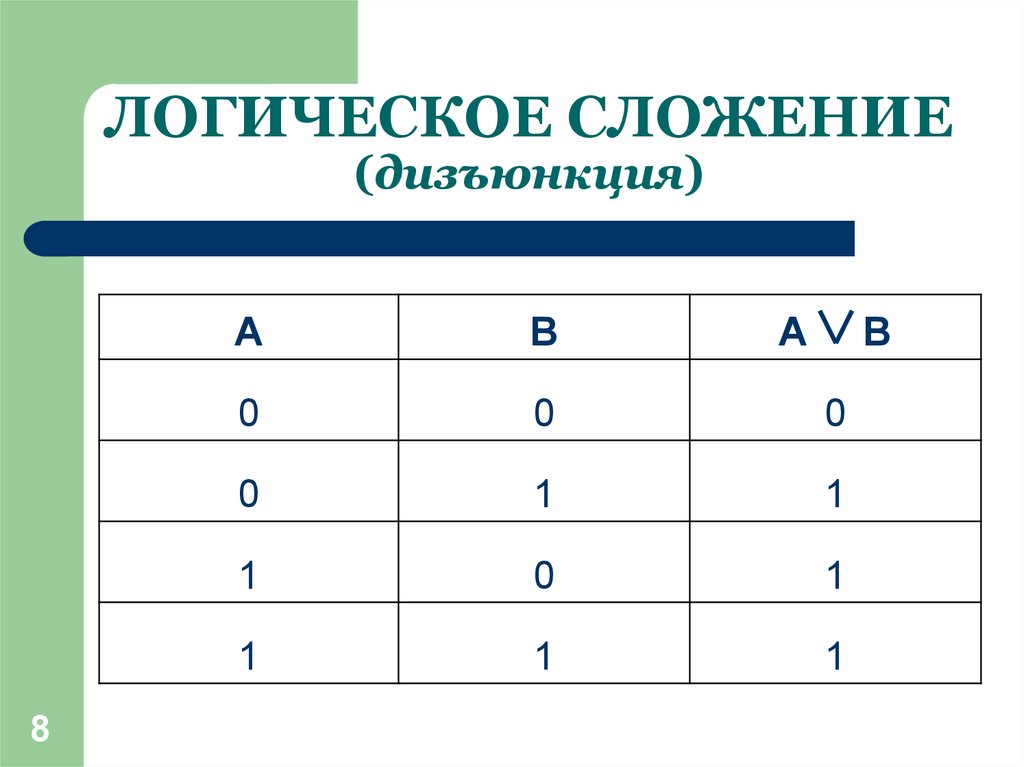
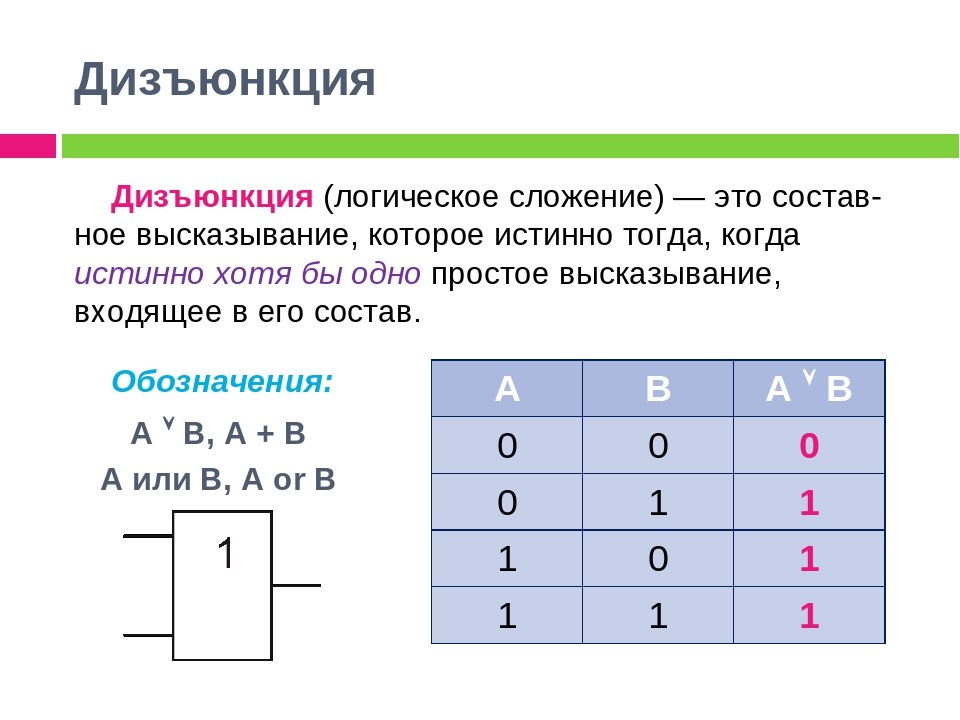
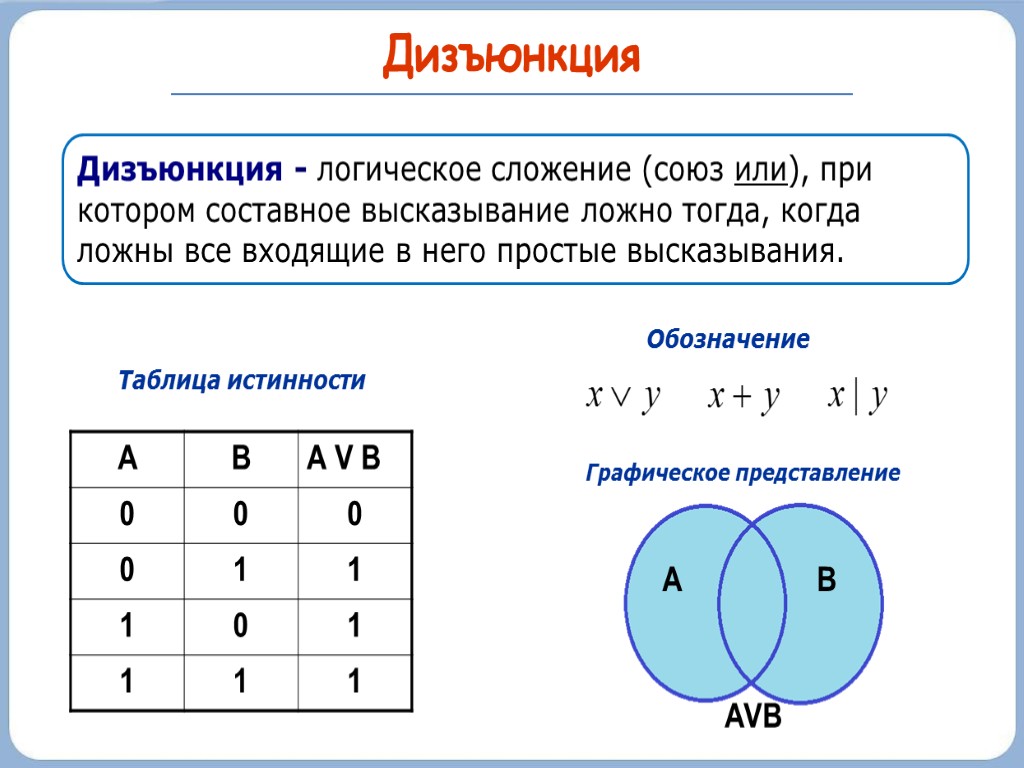
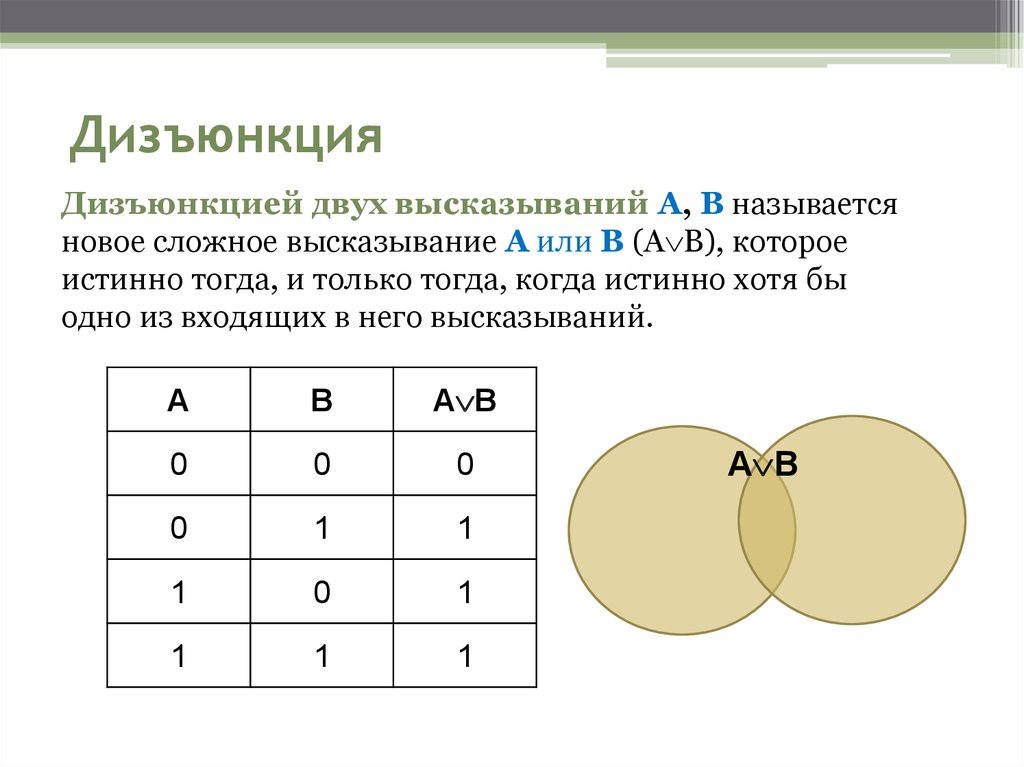
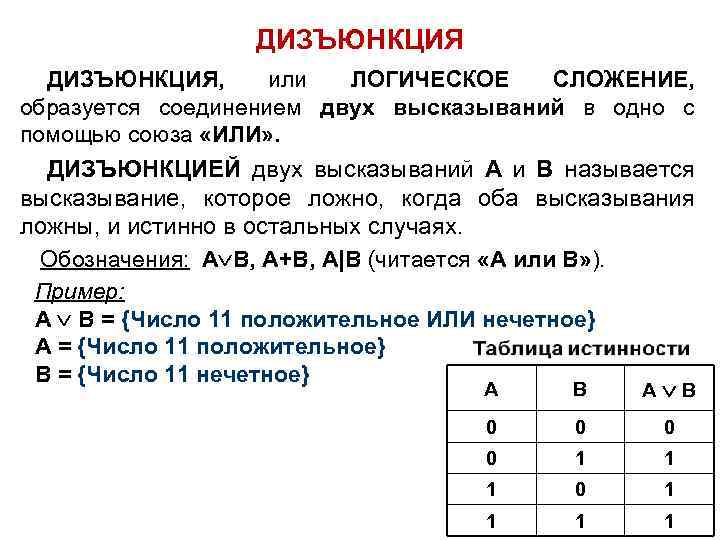
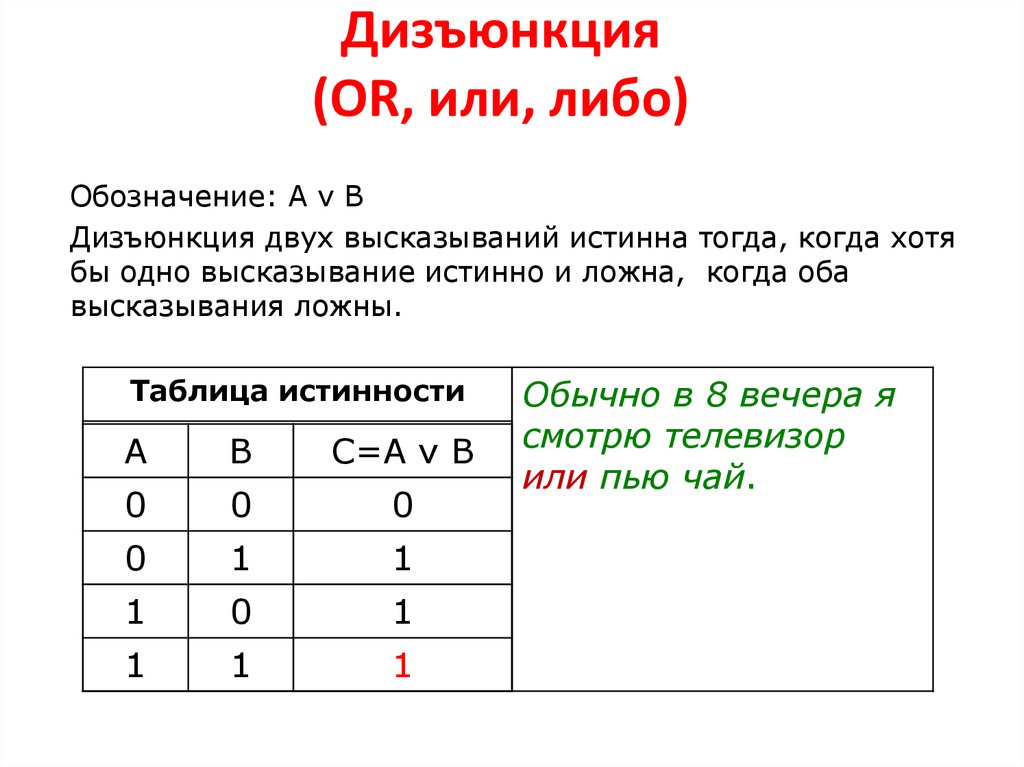
Логическая функция MAX в двухзначной (двоичной) логике называется дизъюнкция (логи́ческое «ИЛИ», логи́ческое сложе́ние или просто «ИЛИ»). При этом результат равен наибольшему операнду.
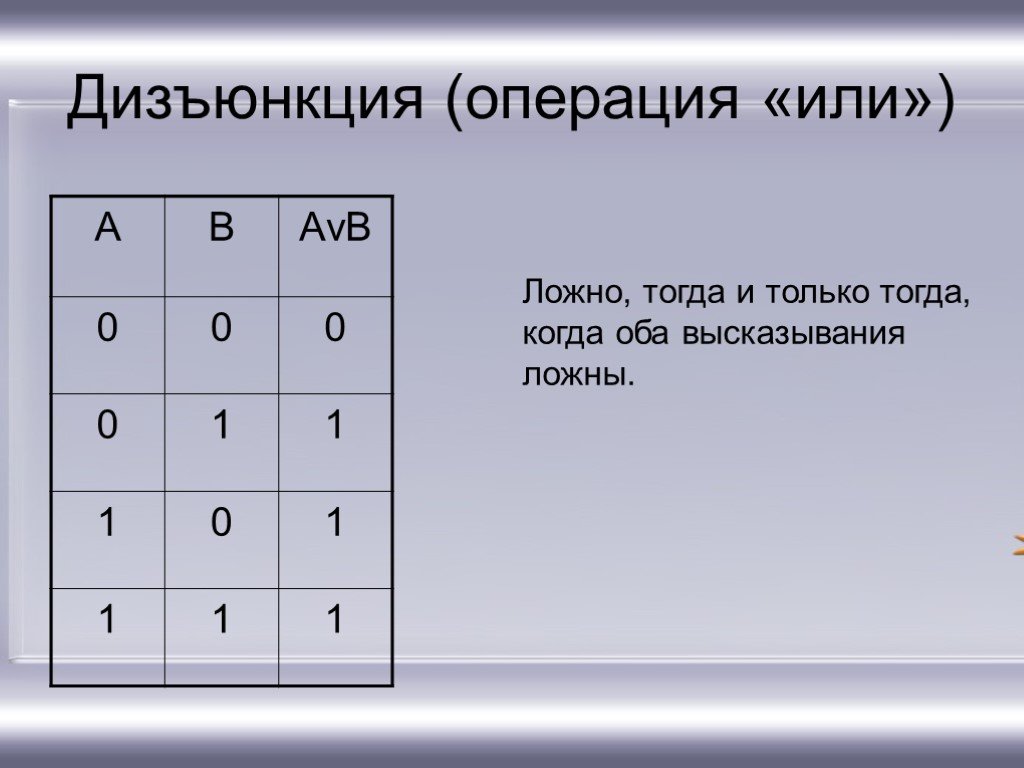
В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Таким образом, результат равен {\displaystyle 0}, если все операнды равны {\displaystyle 0}; во всех остальных случаях результат равен 1{\displaystyle 1}.
| Таблица истинности | ||
|---|---|---|
| a{\displaystyle a} | b{\displaystyle b} | a∨b{\displaystyle a\lor b} |
| {\displaystyle 0} | {\displaystyle 0} | {\displaystyle 0} |
| {\displaystyle 0} | 1{\displaystyle 1} | 1{\displaystyle 1} |
| 1{\displaystyle 1} | {\displaystyle 0} | 1{\displaystyle 1} |
| 1{\displaystyle 1} | 1{\displaystyle 1} | 1{\displaystyle 1} |
Таблица истинности для тернарной (трёхоперандной) дизъюнкции:
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a∨b∨c{\displaystyle a\lor b\lor c} |
|---|---|---|---|
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 |
Булева алгебра
В булевой алгебре сложение по модулю 2 — это функция двух, трёх и более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений ,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при этом необходимо доопределять старшинство, например, true>false{\displaystyle true>false}.
Таблицы истинности:
для бинарного сложения по модулю 2 (применяется в двоичных полусумматорах):
| a{\displaystyle a} | b{\displaystyle b} | a⊕b{\displaystyle a\oplus b} |
|---|---|---|
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Правило: результат равен {\displaystyle 0}, если оба операнда равны; во всех остальных случаях результат равен 1{\displaystyle 1}.
для тернарного сложения по модулю 2 (применяется в двоичных полных сумматорах):
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a⊕b⊕c{\displaystyle a\oplus b\oplus c} |
|---|---|---|---|
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | 1 | 1 |
Правило: результат равен {\displaystyle 0}, если нет операндов, равных 1{\displaystyle 1}, либо их чётное количество.
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:
- a→a∨b{\displaystyle a\to a\lor b}
- b→a∨b{\displaystyle b\to a\lor b}
- (a→c)→((b→c)→((a∨b)→c)){\displaystyle (a\to c)\to ((b\to c)\to ((a\lor b)\to c))}
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции
Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Булева алгебра
Логическая функция MAX в двухзначной (двоичной) логике называется дизъюнкция (логи́ческое «ИЛИ», логи́ческое сложе́ние или просто «ИЛИ»). При этом результат равен наибольшему операнду.
В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Таким образом, результат равен {\displaystyle 0}, если все операнды равны {\displaystyle 0}; во всех остальных случаях результат равен 1{\displaystyle 1}.
| Таблица истинности | ||
|---|---|---|
| a{\displaystyle a} | b{\displaystyle b} | a∨b{\displaystyle a\lor b} |
| {\displaystyle 0} | {\displaystyle 0} | {\displaystyle 0} |
| {\displaystyle 0} | 1{\displaystyle 1} | 1{\displaystyle 1} |
| 1{\displaystyle 1} | {\displaystyle 0} | 1{\displaystyle 1} |
| 1{\displaystyle 1} | 1{\displaystyle 1} | 1{\displaystyle 1} |
Таблица истинности для тернарной (трёхоперандной) дизъюнкции:
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a∨b∨c{\displaystyle a\lor b\lor c} |
|---|---|---|---|
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 | ||
| 1 | 1 | 1 | |
| 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 |