Об этой статье
Соавтор(ы):
Штатный редактор wikiHow
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества. Количество просмотров этой статьи: 89 447.
Категории: Геометрия
English:Find the Width of a Rectangle
Italiano:Calcolare l’Altezza di un Rettangolo
Español:hallar el ancho de un rectángulo
Français:calculer la largeur d’un rectangle
Português:Calcular a Largura de um Retângulo
Deutsch:Die Breite eines Rechtecks berechnen
Bahasa Indonesia:Menghitung Lebar Persegi Panjang
Nederlands:De breedte van een rechthoek bepalen
ไทย:หาความกว้างของรูปสี่เหลี่ยมผืนผ้า
Tiếng Việt:Tìm chiều rộng hình chữ nhật
العربية:إيجاد عرض المستطيل
中文:求矩形的宽
日本語:長方形の幅を計算する
हिन्दी:आयत की चौड़ाई पता करें (Find the Width of a Rectangle)
한국어:직사각형 가로 길이 구하는 법
Печать
Пример расчета параметров
У прямоугольника известна диагональ (m=10) и периметр (Р=28). Необходимо узнать длину его сторон. Решать задачу нужно по такому алгоритму:
- Диагональ находится по следующему выражению: m^2=k^2+l^2.
- Формула для вычисления периметра: P=2(k+l).
- Составить систему уравнений для нахождения сторон: 100=k^2+l^2 и 28=2(k+l).
- Выразить из второго уравнения одну из сторон: k=14-l.
- Подставить в первое: (14-l)^2+l^2=100.
- Раскрыть скобки: 196-28l+l^2+l^2=2l^2-28l+196=100.
- Уравнение имеет такой вид: l^2-14l+48=0.
- Вычислить его корни: l1=6 и l2=8.
- Подставить в четвертый пункт и посчитать стороны: l=6 и к=8.
Следует отметить, что расчет корней производится подстановкой, при которой возникают дубли решений. Среди них требуется выбрать любых две пары. Исходя из девятого пункта, можно рассчитать значение площади, зная две стороны. Используя формулы, можно находить и другие параметры. Например, высчитать значение острого угла.
Таким образом, перед решением задач по геометрии математики рекомендуют правильно идентифицировать геометрическую фигуру при помощи признаков, а затем использовать какие-либо соотношения.
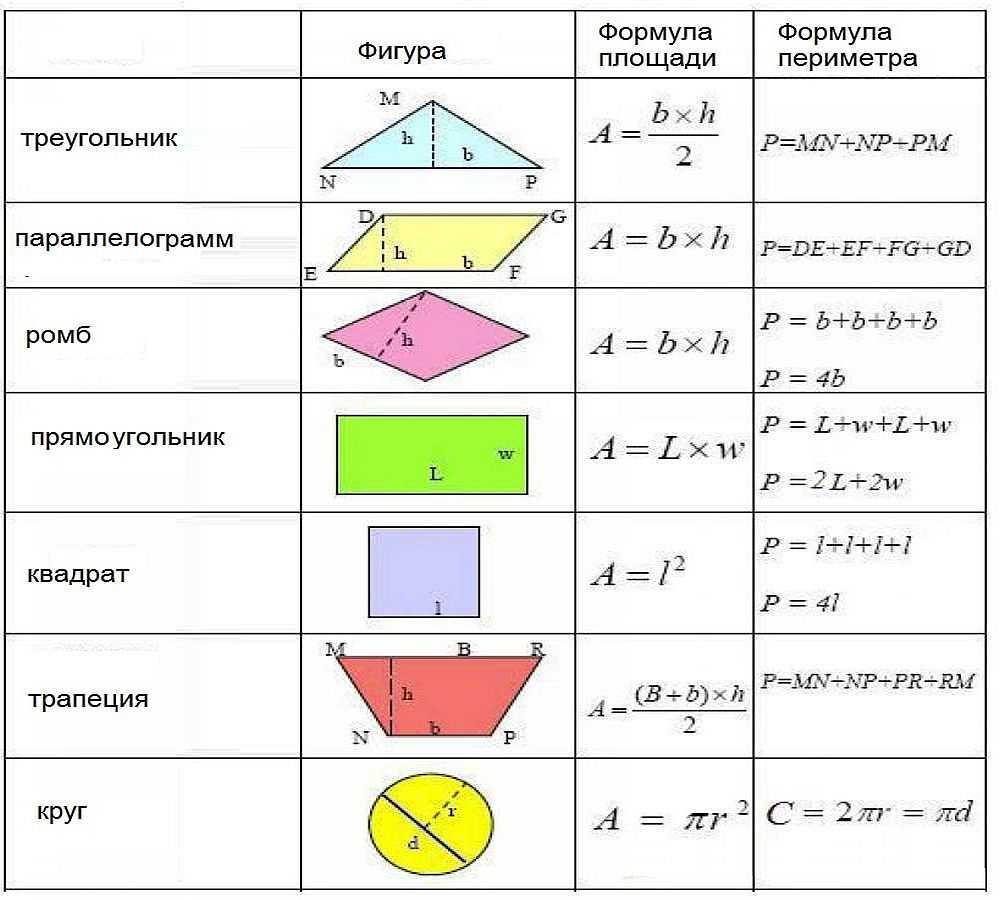
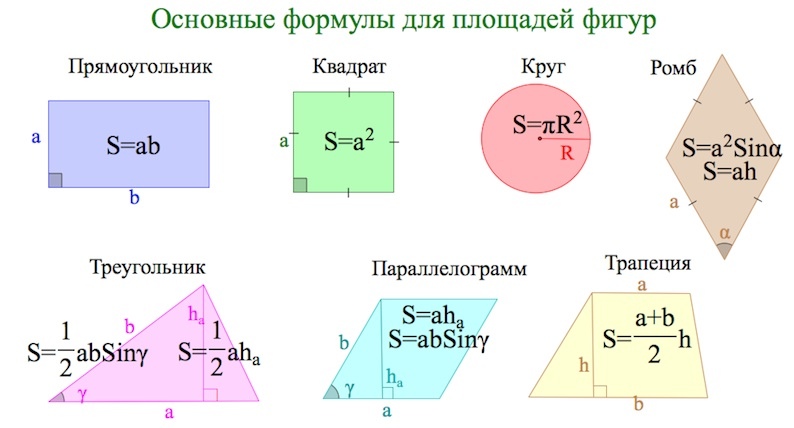
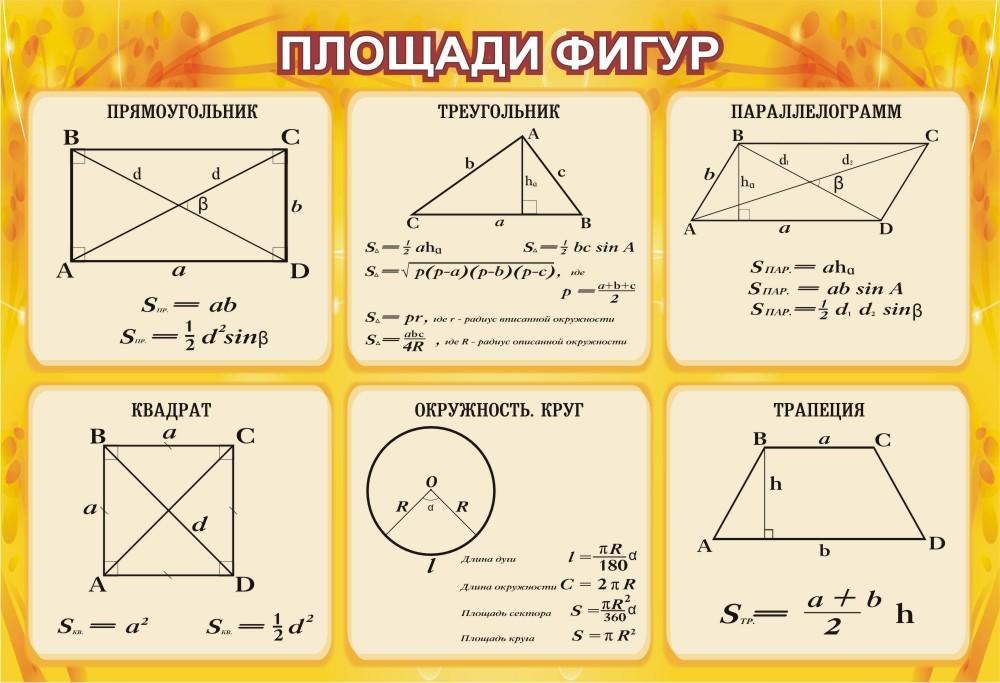
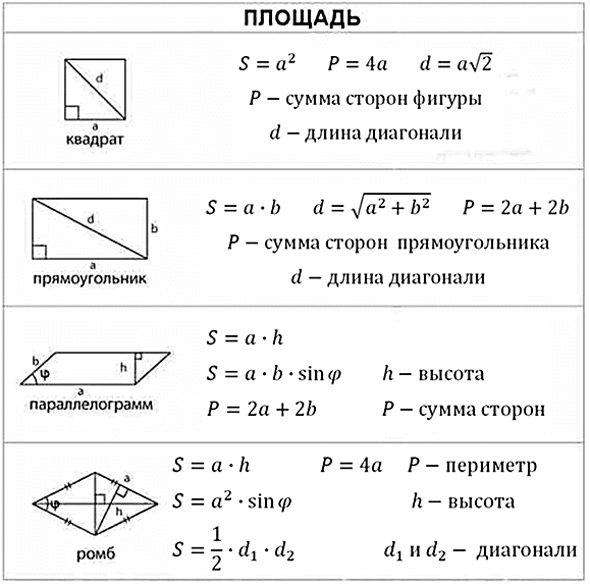
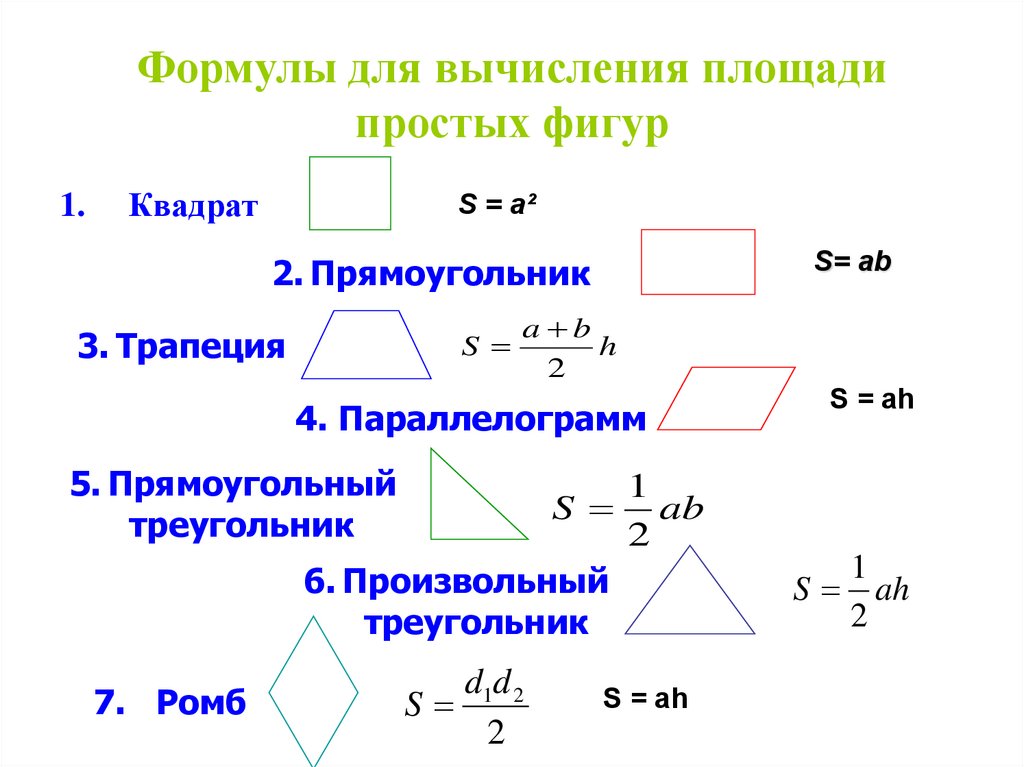
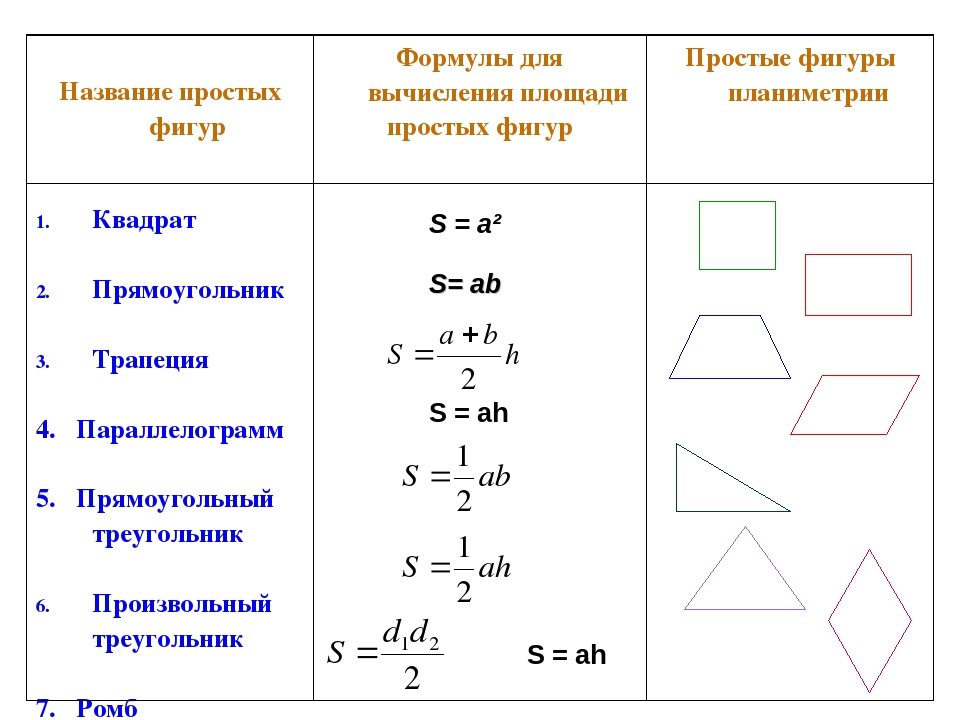
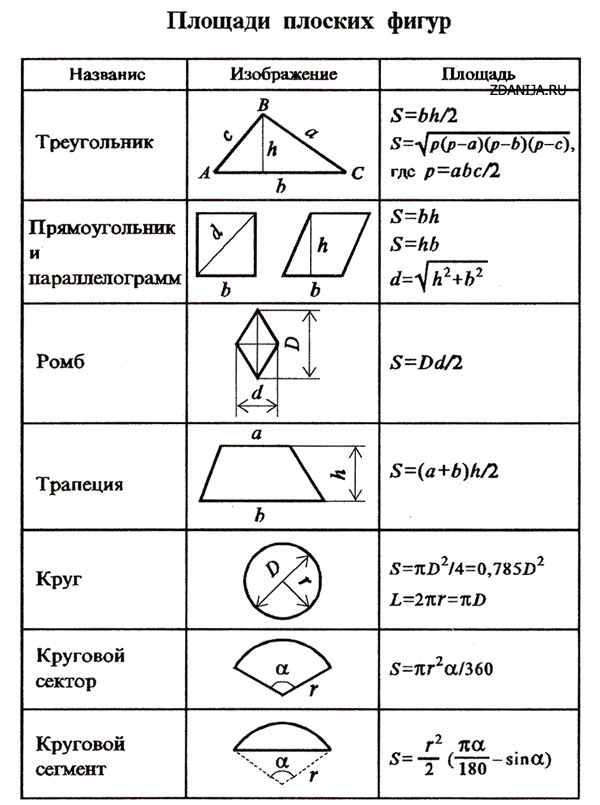
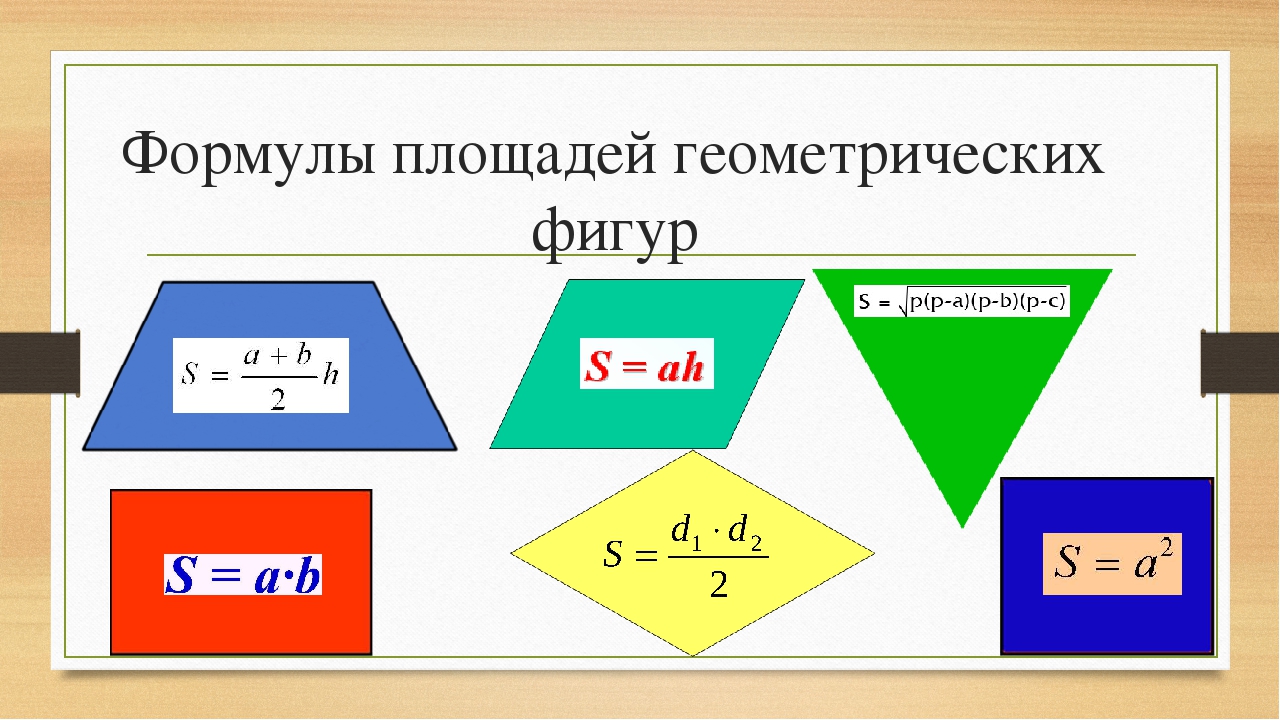
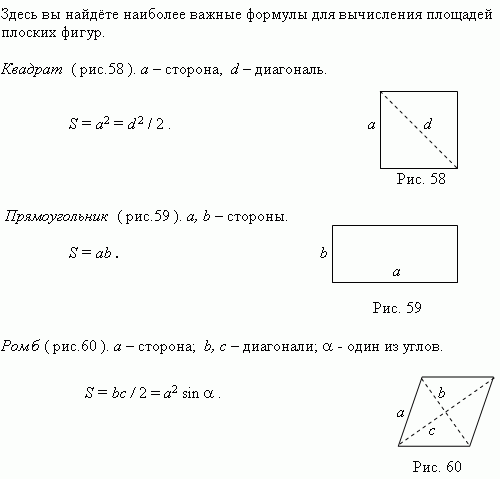
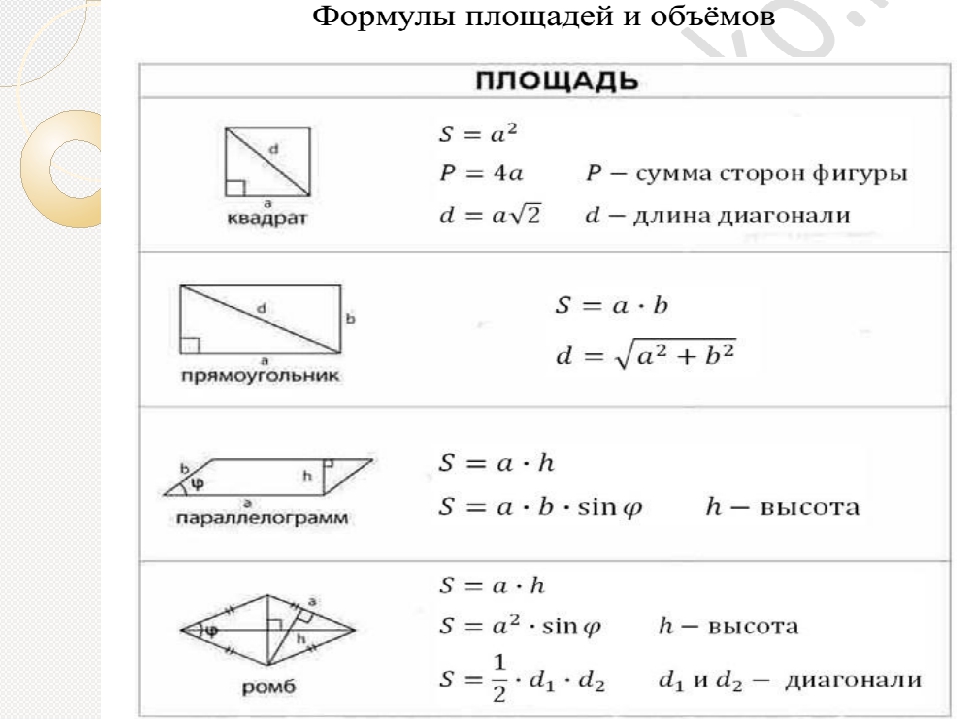
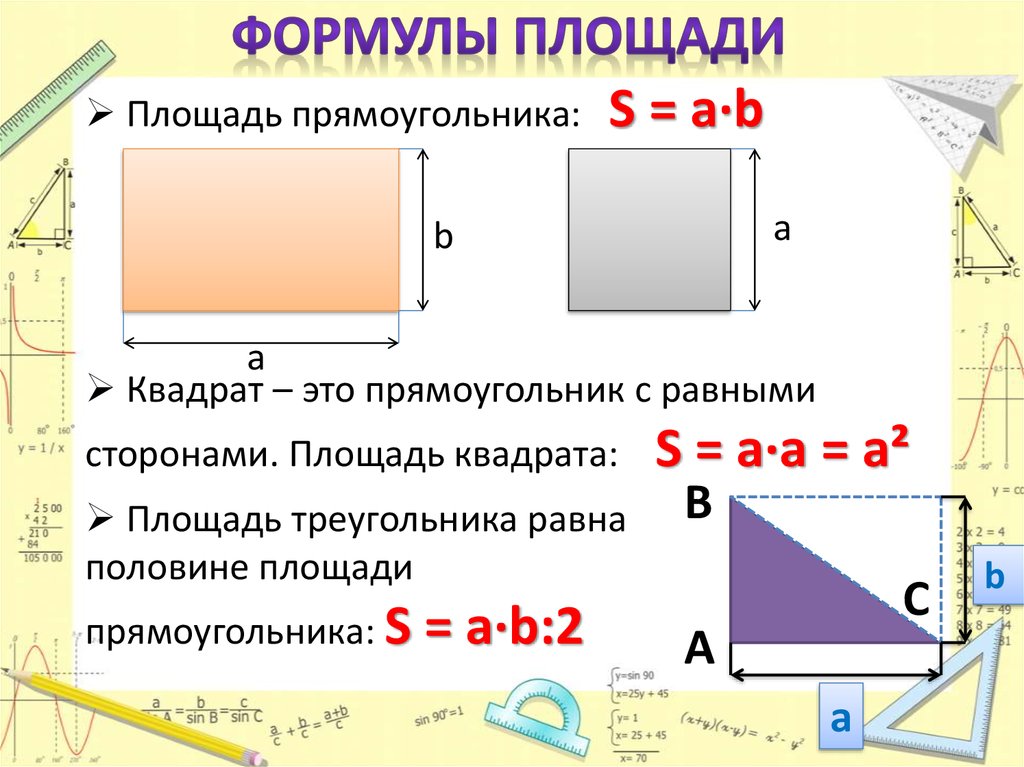
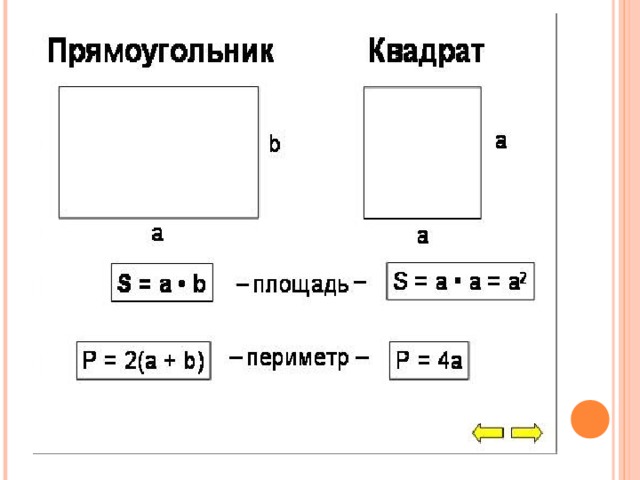
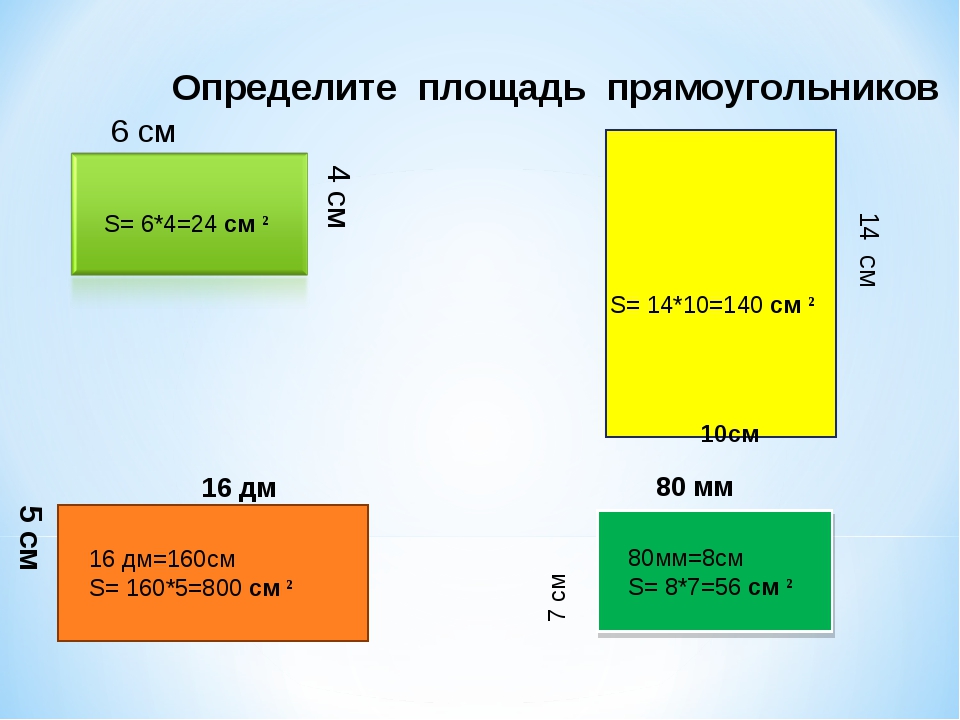
Формула площади прямоугольника
Площадь прямоугольника обычно определяют как произведение длины на ширину. Эта формула выводится через разделение фигуры диагональю на два прямоугольных треугольника. Площадь каждой из фигур это половина произведения катетов. Общая площадь двух фигур целое произведение катетов. Этими катетами как раз и являются длина и ширина прямоугольника.
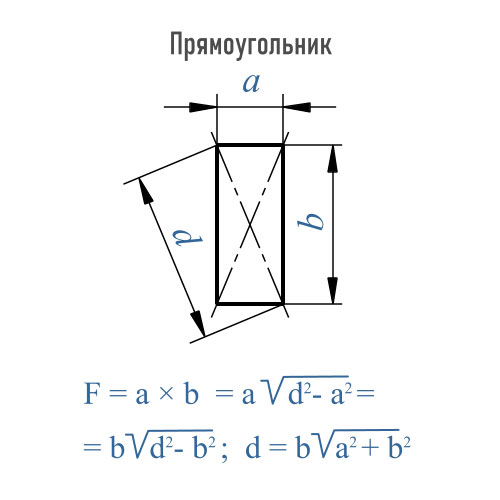
Но случаются ситуации, когда приходится искать площадь, но значений длины или ширины нет. Что делать тогда? Воспользоваться общей для всех четырех угольников формулой и найти площадь прямоугольника через диагонали.
Площадь любого выпуклого четырех угольника равняется произведению диагоналей на синус угла между ними. Диагонали прямоугольного треугольника равны между собой, поэтому значения угла и одной диагонали хватит для нахождения площади.
$$S={1\over2}*d^2*sin(a)$$
Внимательно следите за тем, какой именно угол дан в условиях задачи. Необходим острый угол при диагоналях. Если тупой, то можно воспользоваться формулой смежного угла. Если дан какой-либо из углов между стороной и диагональю, то придется искать другие пути решения.
Возможны ситуации, когда нужно найти площадь, а известен угол между диагональю и стороной и значение диагонали и стороны. Тогда нужно найти площадь прямоугольного треугольника через формулу с применением синуса и удвоить ее.
Рис. 3. Площадь прямоугольника.
В этом случае площадь прямоугольника будет равна:
S=d*b*sin(a)
Что мы узнали?
Мы поговорили о площади прямоугольного треугольника. Выделили отдельно формулу площади прямоугольника через диагонали. Поговорили о случаях, когда применение этой формулы невозможно или затруднено и привели альтернативный вариант решения.
Формулы и соотношения
Чтобы ориентироваться в формулах, нужно ввести некоторые обозначения. К ним принадлежат следующие:
- Диагональ — m.
- Стороны — k и l.
- Периметр — P.
- Полупериметр — р.
- Площадь — S.
- Острый угол, который образуют две диагонали — Z, а тупой — Y.
- Диаметр — D.
После этого необходимо рассмотреть основные тождества. Их рекомендуется применять при вычислениях различных параметров фигуры.
К ним относятся такие выражения:
- Периметр: P=2S/к + (2/к)k 2 =2k+2(m 2 -k 2 )^(1/2))=2k+2(D 2 -k 2 )^(1/2)).
- Площадь: S=/2=/2=k=[sin(Z)/2]m^2 .
- Диагонали: m=^(1/2)=(1/k)(S 2 +k 4 )^(1/2).
Кроме того, найти диагональ прямоугольника возможно, используя формулу такого вида: m=((2k+2l) 2 -4(2k(k+l)+8k 2 )^(1/2) * 0,5. Величины «(2k+2l)» можно заменить периметром Р, когда он известен.
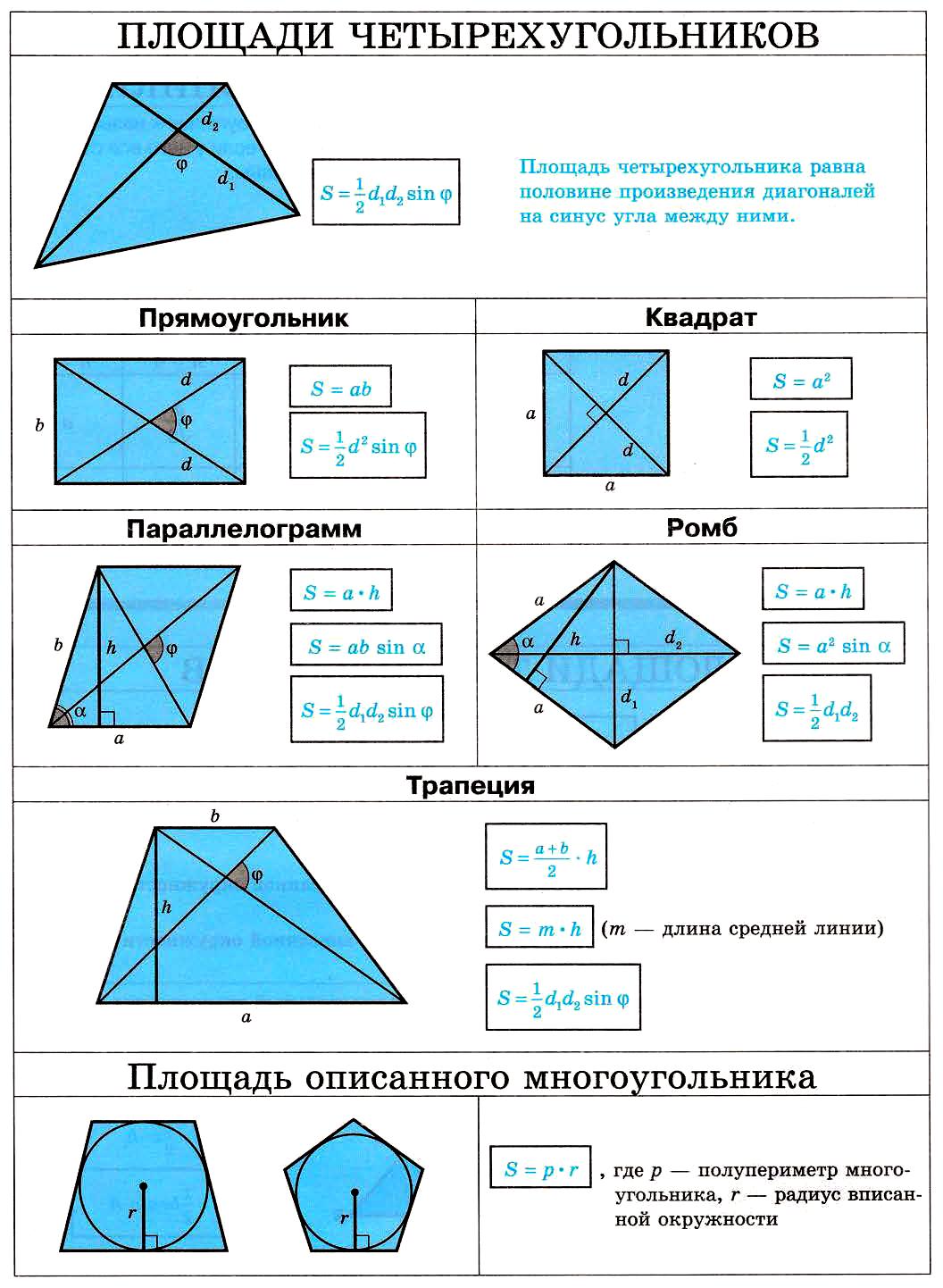
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.
Рис. 2. Диагонали многоугольника.
В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P={n(n-3)\over{2}}$ – где n это число сторон многоугольника.
Проверим для квадрата:
$P={4(4-3)\over{2}}={4\over2}=2$ – все верно.
Рис. 3. Диагонали квадрата.
Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
Общая информация
Прямоугольник — геометрическая плоская фигура, состоящая из четырех попарно параллельных сторон, между которыми образованы прямые углы. Ее можно перепутать с квадратом, имеющим похожие свойства и тождества
При решении задачи очень важно правильно найти фигуру, имеющую определенные признаки определения. Некоторые учащиеся путают последние со свойствами
Эти два термина отличаются между собой.
Методика идентификации
Признак — совокупность некоторых критериев, позволяющих правильно различать фигуры. Прямоугольник возможно идентифицировать по таким правилам:
- Неравенство сторон, являющихся смежными.
- Диагонали при пересечении не образуют угол в 90 градусов.
- Диагонали не являются биссектрисами углов больших треугольников, полученных при пересечении.
- Окружность можно только описать, а не вписать.
Если для искомой фигуры применим хотя бы один из признаков, то ее возможно классифицировать как прямоугольник.
Важные свойства
Свойства — набор или список утверждений и тождеств, используемых при вычислениях требуемых величин, а также для доказательства теорем, а именно:
- Все углы прямые, а их алгебраическая сумма равна 360.
- Несмежные стороны параллельны и равны.
- Точка пересечения диагоналей — центр симметрии и делит их на две части. Кроме того, средняя линия проходит через нее.
- Формула диагонали (m) прямоугольника через стороны p и t: m=(рp+tt]^1/2), т. е. квадратичное значение диагонали равно сумме сторон, каждая из которых умножена на эквивалентное значение.
- Подобность малого и большого треугольников, образованных диагоналями.
- Существует только описанная окружность, диаметр которой эквивалентен диагонали прямоугольника.
- При проведении диагонали образуются два равных треугольника, являющиеся прямоугольными.