Clusterdelta

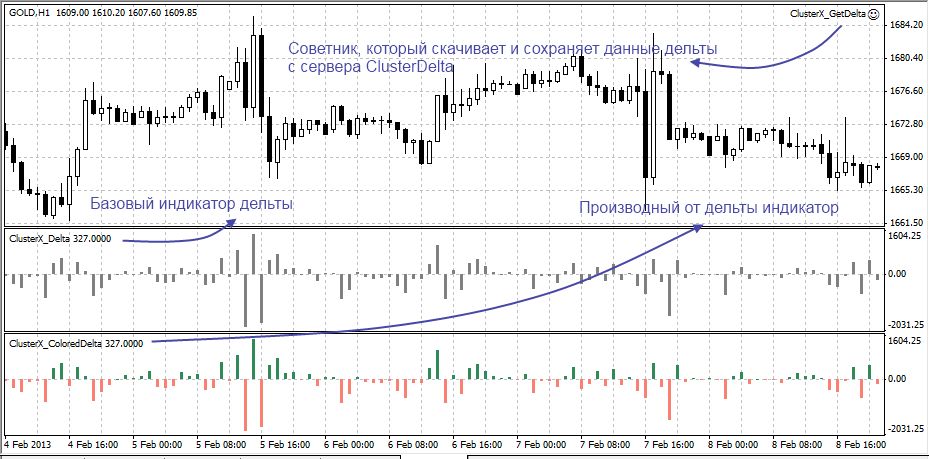
Индикатор Delta

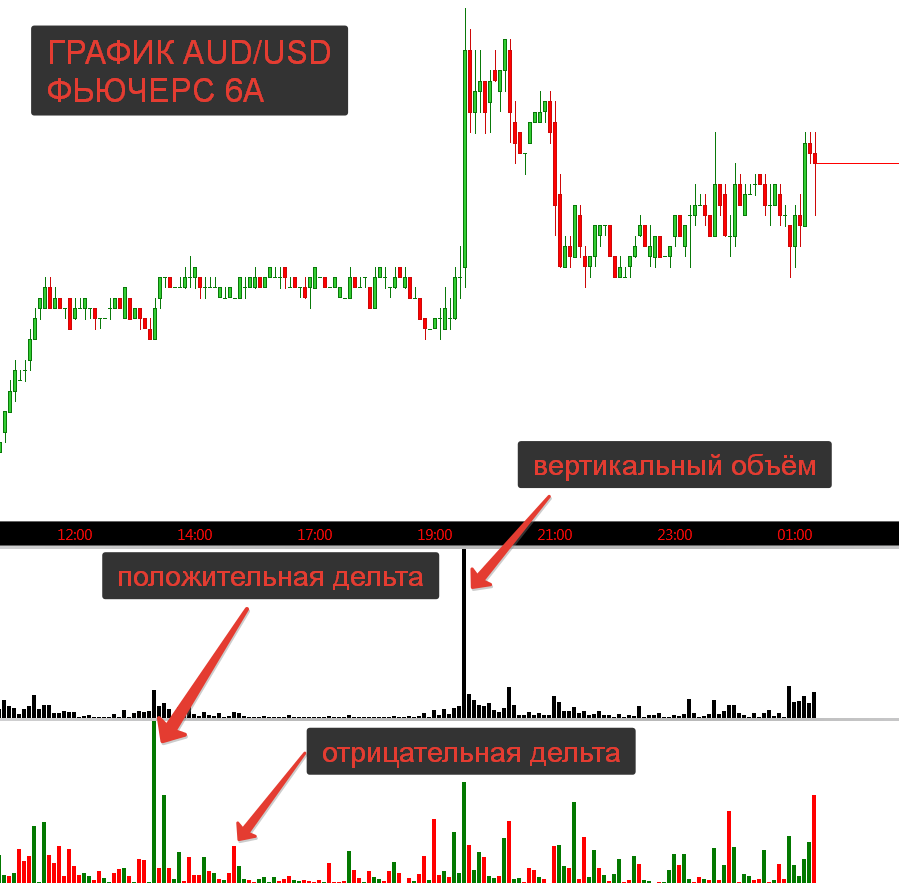
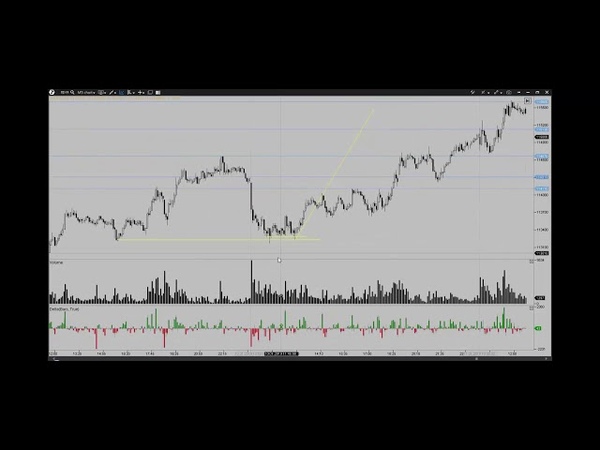
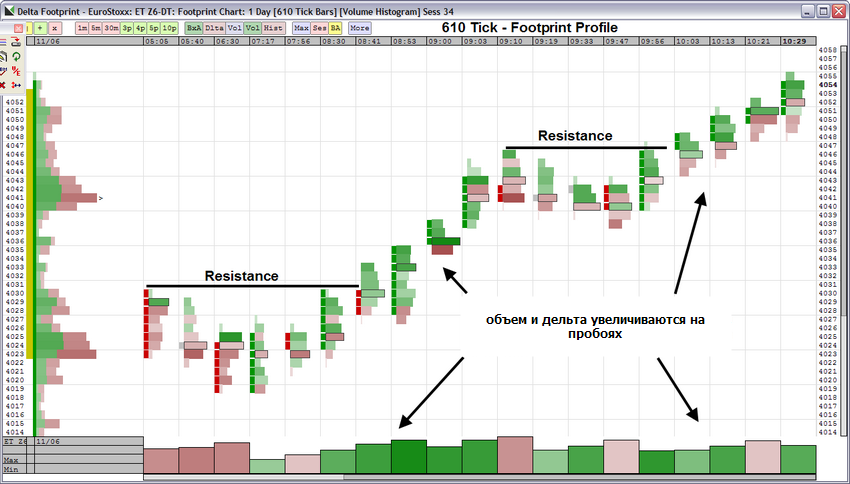
Данный индикатор показывает суммарное значение Дельты для каждой свечи в виде вертикальной гистограммы в нижней части графика, причем не важно какой тип графика (фрейм) вы используете. Бары индикатора Delta, могут быть как положительными, так и отрицательными

Положительная Дельта отмечена барами зеленого цвета и характерна для «положительного» потока ордеров, в результате которого покупатели «агрессивнее» проявили себя в конкретной свече. Отрицательная Дельта отмечена барами красного цвета и характерна для «отрицательного» потока ордеров, в результате которого продавцы «агрессивнее» проявили себя в конкретной свече

Бары индикатора Delta, могут быть как положительными, так и отрицательными. Положительная Дельта отмечена барами зеленого цвета и характерна для «положительного» потока ордеров, в результате которого покупатели «агрессивнее» проявили себя в конкретной свече. Отрицательная Дельта отмечена барами красного цвета и характерна для «отрицательного» потока ордеров, в результате которого продавцы «агрессивнее» проявили себя в конкретной свече.

График №2. 5-минутный таймфрейм фьючерса на евро (тикер 6E). График Футпринт Bid x Ask и индикатор Delta в нижней части графика

Обратите внимание, что на Графике №2 у некоторых медвежьих свечей положительная зеленая Дельта. То есть несмотря на то, что в данных свечах преобладали рыночные покупки, цена все же снижалась

Такое расхождение объясняется тем, что на рынке в тот момент времени присутствовал крупный продавец, который открывая свои рыночные продажи, защищал их лимитными ордерами на продажу (англ. sell limit order).

В результате таких действий, все покупки, которые приходили в то время от «агрессивных» покупателей, пытавшихся сопротивляться нисходящему движению цены, исполнялись на защитных лимитных ордерах крупного продавца. Действуя таким образом, крупному продавцу, чтобы толкнуть цену в прибыльном для него направлении, не нужно было открывать крупных рыночных сделок на продажу.

Его продажи в значительной степени открывались на защитных лимитных ордерах, которые полностью поглощали все рыночные покупки. Стоит отметить, что цена продолжала снижаться еще и потому, что покупатели, в свою очередь, не стремились защитить свои рыночные покупки лимитными ордерами на покупку или же ставили их в недостаточном количестве для сдерживания продавцов.

Если вдруг выявление таких расхождений из общего потока рыночной информации кажется вам сложным, то платформа ATAS сможет максимально облегчить эту задачу. На Графике №3 фьючерса E-mini S&P 500, показатели индикатора Delta строятся с использованием двух фильтров: направление баров — медвежье , тип дельты — положительная .

График №3. 30-минутный таймфрейм фьючерса E-mini S&P 500 (тикер ES). График Футпринт Bid x Ask и индикатор Delta в нижней части графика с использованием фильтров

В данном примере крупный игрок не пускал «агрессивных» покупателей выше уровня 2644.25 сдерживая их своими лимитными ордерами на продажу. Об этом нам говорит ряд медвежьих свечей с положительной Дельтой. Все рыночные покупки поглощались лимитными ордерами, расположенными у верхней границы консолидации.

Когда вы наблюдаете на рынке подобные ситуации помните, что часто они свидетельствуют о присутствии крупного, или как еще говорят, институционального игрока. Как вы уже наверняка знаете из наших предыдущих статей, только крупный игрок, в отличии от ритейл трейдеров, располагает достаточными финансовыми ресурсами для защиты своих открытых позиций. Уже два этих примера демонстрируют колоссальное преимущество торговли с использованием продвинутых инструментов анализа потока ордеров платформы ATAS.

Физическая интерпретация

Вблизи заряженной точки поле бесконечно, ряды Тейлора для поля не сходятся, поэтому вводят специальные функции. Одной из таких функций является дельта-функция. Вопрос о поле точечной заряженной частицы сравнительно сложен, поэтому рассмотрим сначала более простой пример.

Мгновенное ускорение

Пусть частица, способная перемещаться вдоль прямой, при ударе пренебрежимо малой длительности скачком приобретает какую-то скорость. Зададимся вопросом: как рассчитать ускорение, приобретённое телом? Построим график зависимости изменения скорости от времени. График будет иметь следующий вид:

Данный график почти всюду является графиком функции Хевисайда. Производная функции Хевисайда является единичной дельта-функцией, график которой условно можно изобразить как

Данный график отображает бесконечное ускорение при мгновенном наборе скорости. В общем случае ускорение при ударе можно записать как

a(t)=νδ(t−ta). {\displaystyle a(t)=\nu \delta (t-t_{a}).\ }

Масса материальной точки

Если нужно найти суммарную массу (или заряд) некоторого непрерывного распределения плотности (или плотности заряда) m=∫ρcontin,{\displaystyle m=\int \rho _{\mathrm {contin} },} содержащего, кроме того, точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:

m=∫ρcontin(x)dV+∑iqi{\displaystyle m=\int \rho _{\mathrm {contin} }(\mathbf {x} )\,dV+\sum _{i}q_{i}}

где x{\displaystyle \mathbf {x} } — радиус-вектор положения рассматриваемого заряда, записывать просто:

m=∫ρ(x)dV,{\displaystyle m=\int \rho (\mathbf {x} )\,dV,}

имея в виду, что ρ(x){\displaystyle \rho (\mathbf {x} )} имеет как непрерывную, так и дельтообразные, то есть, сосредоточенные в точке, (по одной для каждой точечной массы) составляющие:

ρ(x)=ρcontin(x)+∑iqiδ(x−xi).{\displaystyle \rho (\mathbf {x} )=\rho _{\mathrm {contin} }(\mathbf {x} )+\sum _{i}q_{i}\delta (\mathbf {x} -\mathbf {x} _{i}).}

Другие примеры

• Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом пределе (ℏ→{\displaystyle \hbar \rightarrow 0}) квантовой механики волновые функции локализуются в волновые пакеты с дельтообразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
• Преобразование Фурье единицы является дельта-функцией. Это позволяет более удобно и математически строго формулировать различные задачи, связанные с преобразованием Фурье, которые очень многочисленны: волновая оптика, акустика, теория колебаний. В квантовой механике преобразования Фурье волновых функций играют первостепенную принципиальную и техническую роль, именно для неё Дирак впервые ввёл дельта-функцию.
• Дельта-функции играют роль собственных функций оператора с непрерывным спектром в представлениях, где этот оператор диагонален. Таким образом, они играют роль базиса в диагональном представлении оператора.
• Важным применением дельта-функции является их участие в аппарате функций Грина линейных операторов. Для линейного оператора L, действующего на обобщённые функции над многообразием M, уравнение, определяющее функцию Грина g с источником в точке x,{\displaystyle x_{0},} имеет вид

Lg(x,x)=δ(x−x).{\displaystyle L\,g(x,\;x_{0})=\delta (x-x_{0}).}

Особенно часто встречается применение этого аппарата к оператору Лапласа (электростатика, теплопроводность, диффузия, механическая теория упругости) и подобным ему операторам, таким как Оператор Д’Аламбера (акустика, электродинамика, квантовая теория поля, где функция Грина часто носит специальное название пропагатора).

Для лапласиана в R3{\displaystyle \mathbb {R} ^{3}} функцией Грина является функция 1/r, так что

Δ(1r)=−4πδ(r),{\displaystyle \Delta \left({\frac {1}{r}}\right)=-4\pi \delta (\mathbf {r} ),}

где r — расстояние до начала координат. Этот факт используется для доказательства того, что выражение для скалярного потенциала

Φ(x)=−∫ϱ(x′)|x−x′|d3x′{\displaystyle \Phi (\mathbf {x} )=-\int {\frac {\varrho (\mathbf {x} ^{\prime })}{\left|\mathbf {x} -\mathbf {x} ^{\prime }\right|}}\,d^{3}x^{\prime }}

удовлетворяет уравнению Пуассона:

ΔΦ=−4πϱ.{\displaystyle \Delta \Phi =-4\pi \varrho .}

Динамическая дельта в качестве уровней поддержки/сопротивления

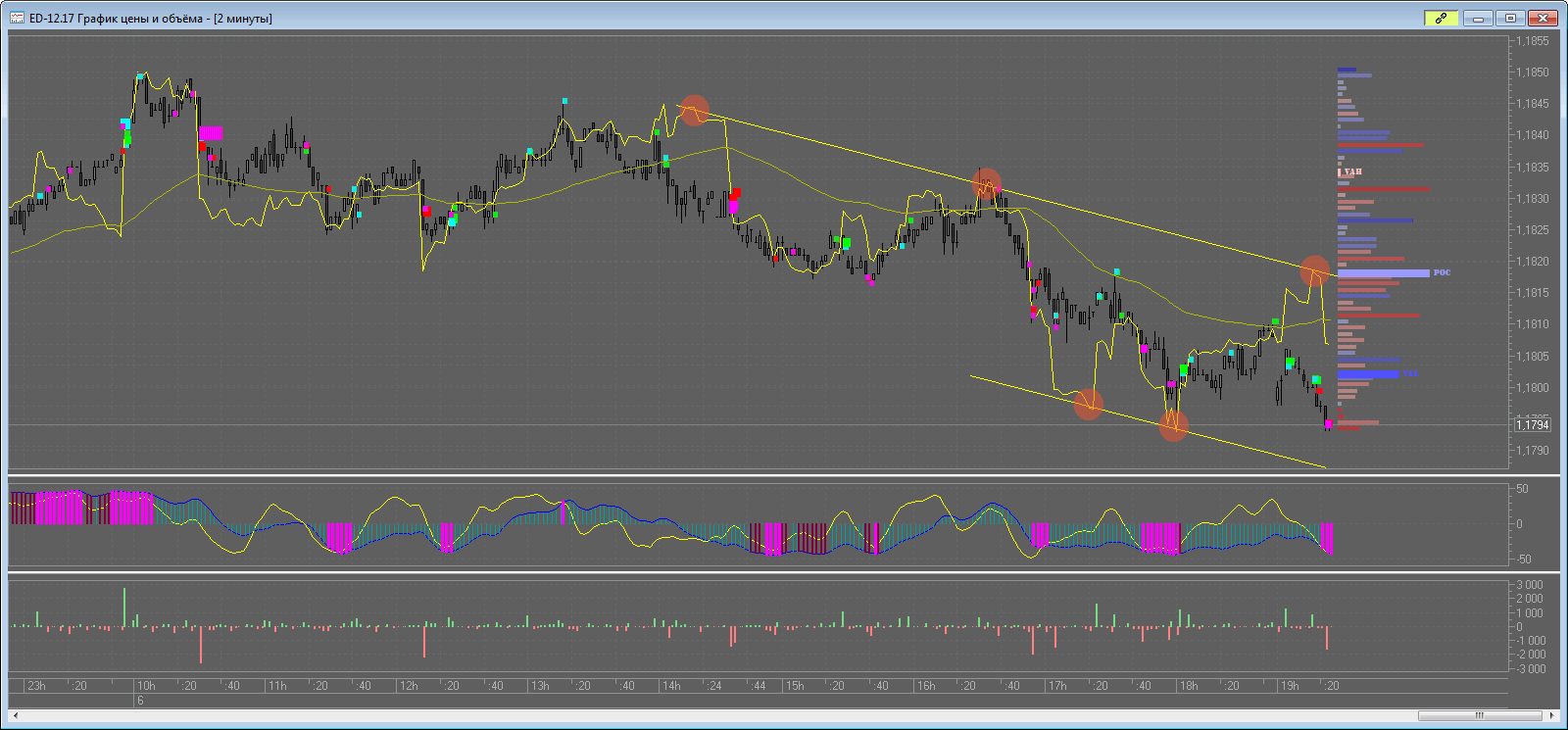
Здесь я опишу ситуацию, которую наблюдал сегодня. С динамическим профилем (дельты, бид-аск) я ранее не работал, а тут решил присмотреться.

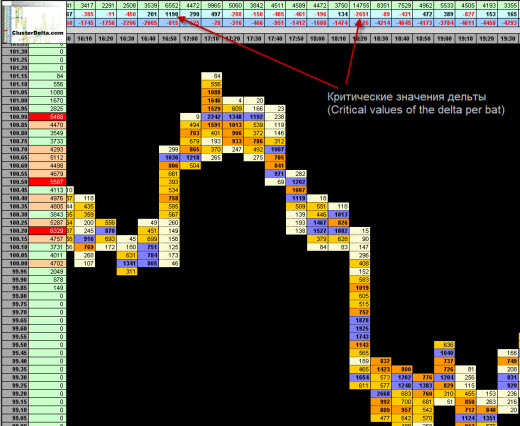
Открываю SbPro (об этой платформе расскажу в отдельном посте), наношу динамическую дельту на кластерный график.

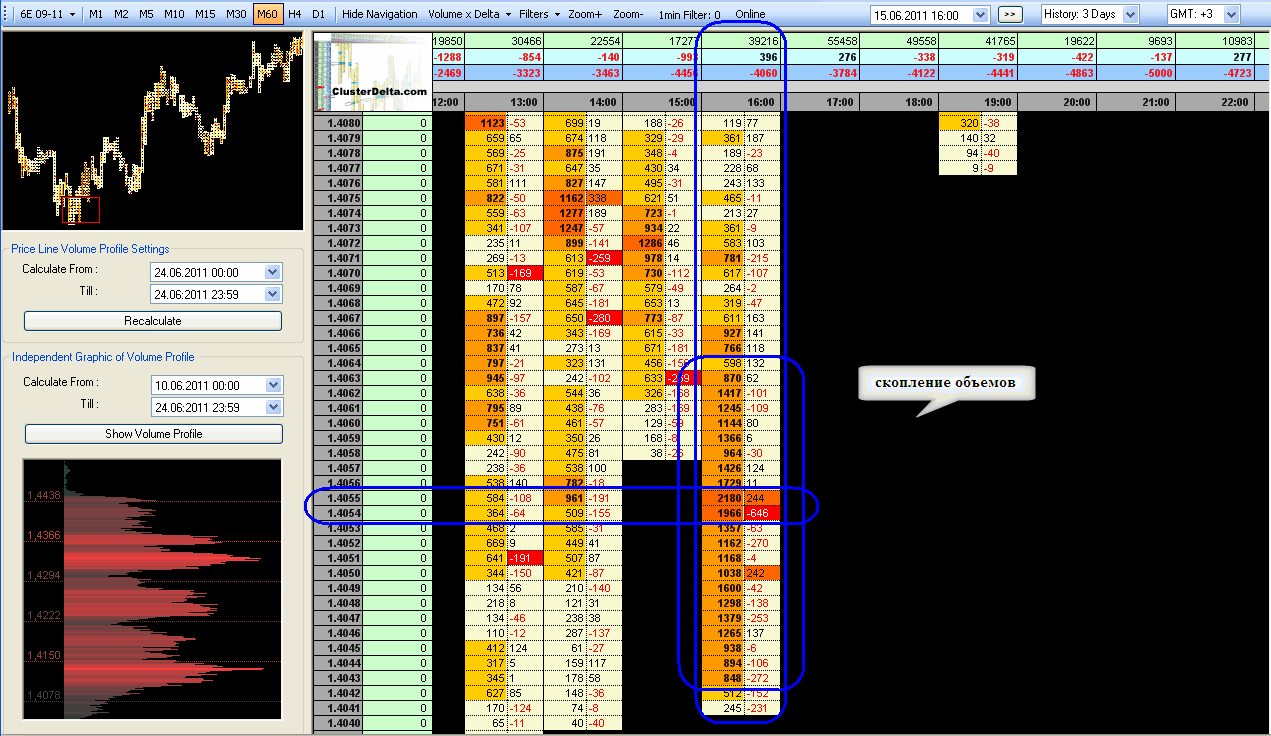
Динамическая дельта в бинарных опционах

Да, картинка постфактум, но все же, стоит обратить внимание на объем 158 и как он отработал. Сначала этот уровень выступал в качестве сопротивления, потом же он стал поддержкой

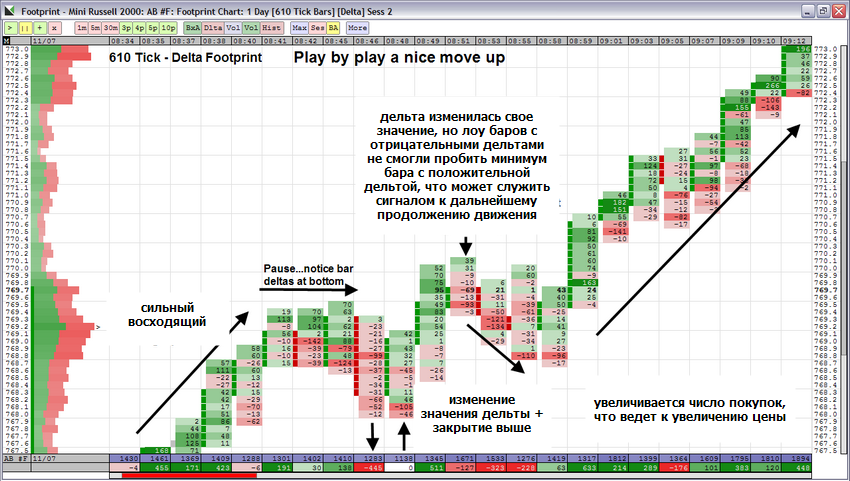
Вот как это выглядит на графике в виде баров:

Отработка дельта уровня

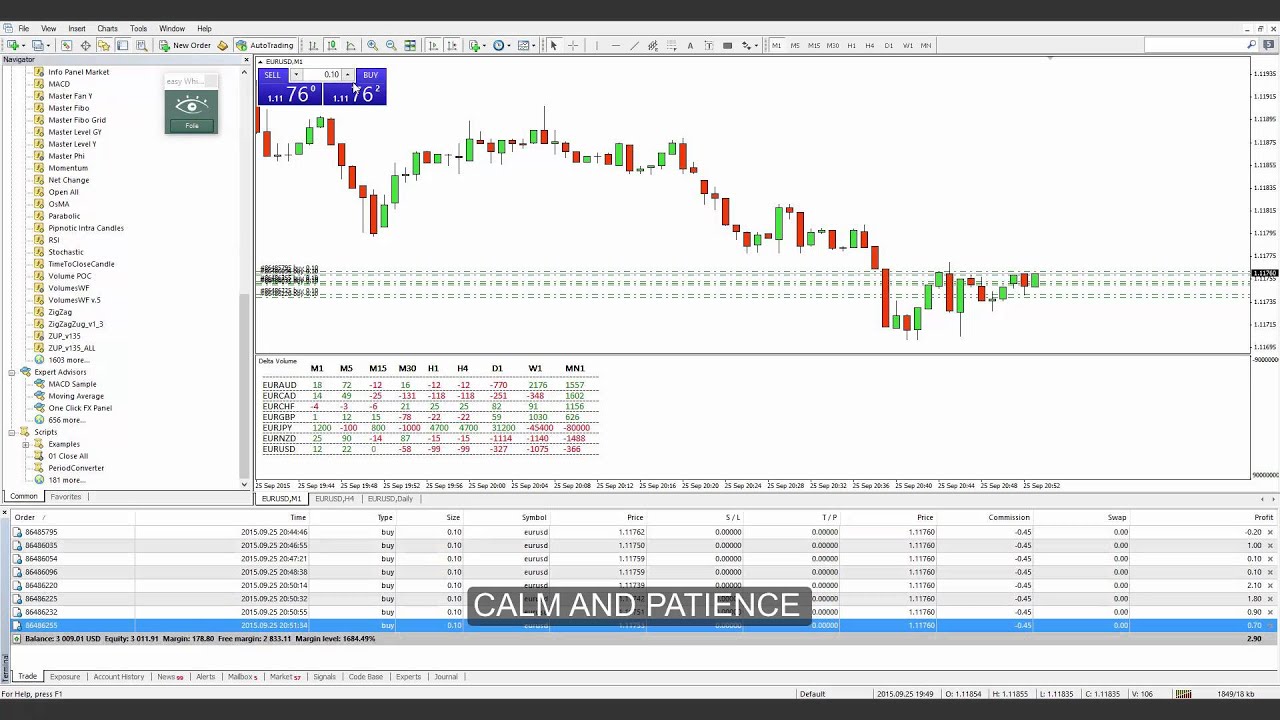
Больше всего здесь мне понравился момент, когда цена ложно пробила этот уровень и дальше пошла вверх (цифра 5). Наблюдал при этом одновременно за 5-минутным и 30-секундными графиками. На 30-секундном это выглядело так:

Отработка уровня дельты на 30-секундном графике

И именно в этом случае можно было смело входить на 3-5 минут (поскольку это 30-секундный график). Как видно на скрине выше, на форексе тоже можно было бы получить неплохой профит, используя эту информацию.

Народный рейтинг брокеров:

• BINARIUM

  Самый лучший и надежный брокер бинарных опционов! Огромный раздел по обучению. Идеально для начинающих трейдеров! Бесплатный демо-счет и денежный бонус за регистрацию:

• FinMax

  Бонусы для новых трейдеров, сигналы, стратегии и быстрый вывод заработанных денег!

Я не входил. Пока только наблюдаю и делаю заметки. Для того и был создан блог.

Конечно, стоит отдельно рассказать, о том, вообще что-такое объемы, дельта, кластеры. При случае займусь.

На данный же момент, для меня важно выделить наилучшие моменты и паттерны, которые я буду использовать в своей торговле. Стремлюсь к тому, чтобы сделать торговлю максимально комфортной для себя

Сейчас в приоритете — выявить паттерны, создать торговый план и четко ему следовать. На данный же момент буду публиковать идеи, наработки, конспекты увиденного и прочитанного.

Торговля на бирже: дельта и кластерный анализ

Итак, с определением дельты мы познакомились, теперь приступим к самому интересному – узнаем, в чём же польза этого инструмента для трейдера.

Зачем трейдеру дельта?

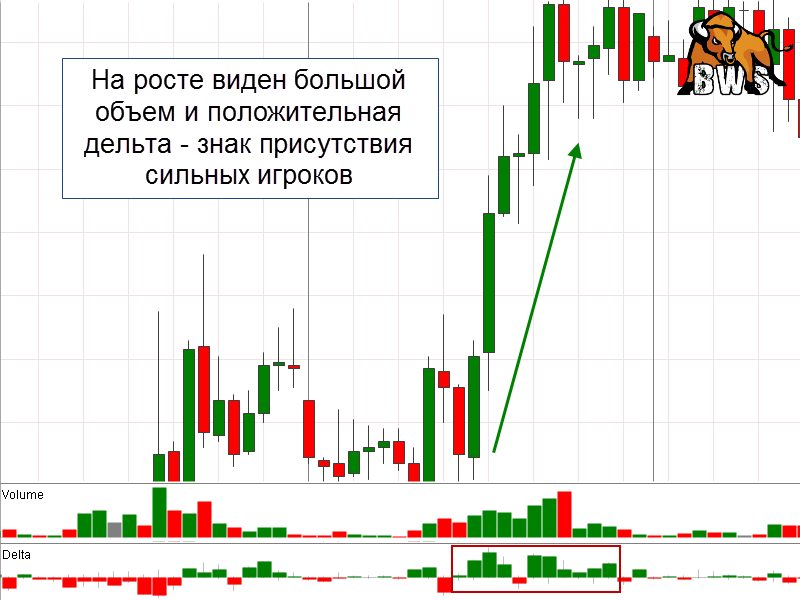
Главное преимущество понимания дельты – это возможность объективно видеть рыночные процессы, даже в ситуациях, когда кривая цены не даёт однозначного ответа. По сути, дельта чётко и однозначно показывает расстановку сил на рынке: если она положительная, у руля покупатели, а если отрицательная – «рулят» продавцы.

А это понимание, в свою очередь, помогает прогнозировать, куда цена пойдёт дальше и входить в сделку в самом начале сильного тренда. Умение работать с дельтой может вывести торговлю на качественно новый уровень.

Примечательное свойство дельты – её можно увидеть даже на очень мелких таймфреймах, а значит, её анализ можно использовать даже в краткосрочных стратегиях торговли и скальпинге, где VSA обычно неэффективен.

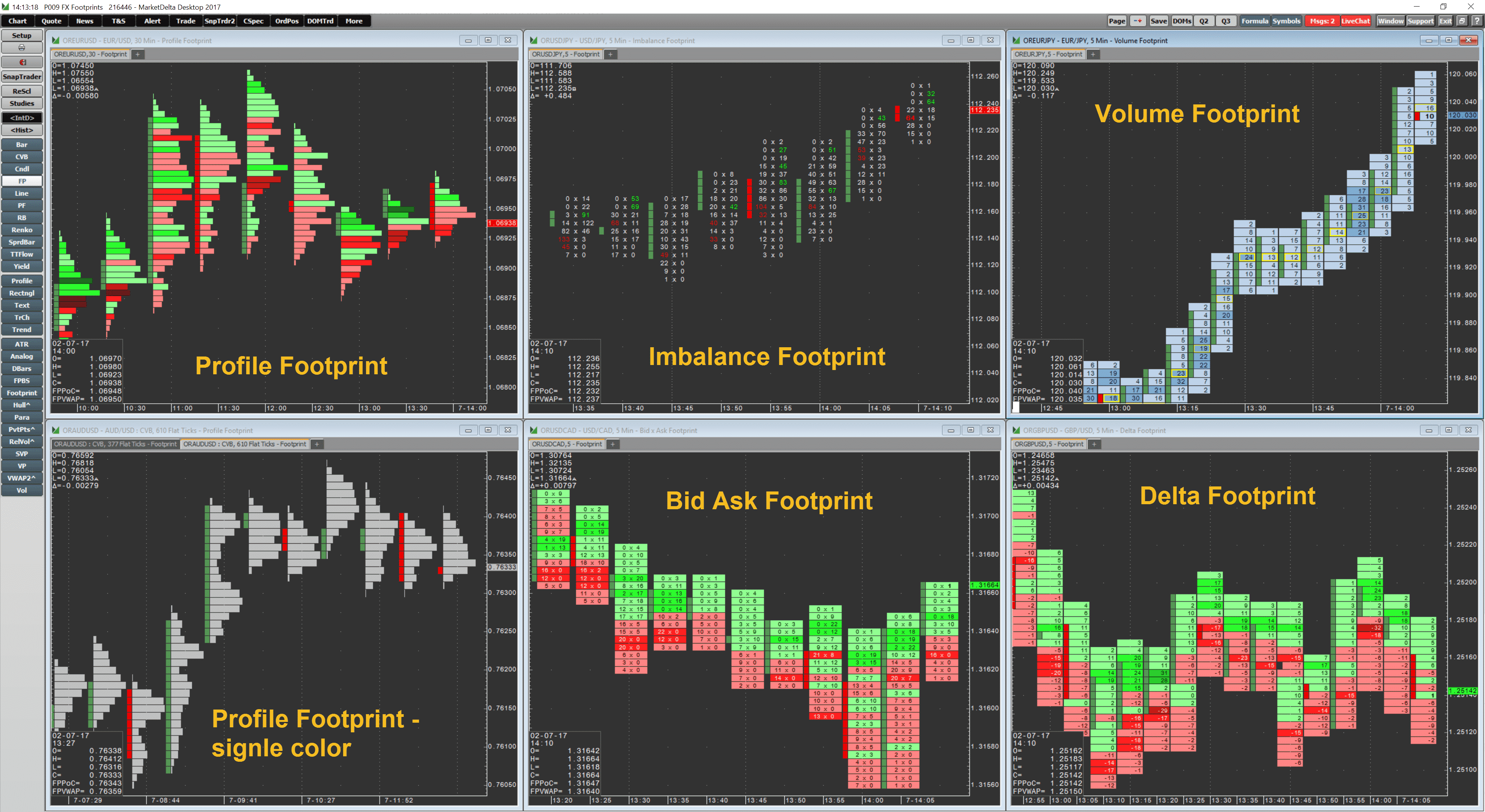
Где искать дельту?

Вообще, чтобы увидеть показатели дельты, необходимо переключиться на график Футпринт. Там, значения дельты вписаны в горизонтальные кластеры, для удобства визуального понимания, окрашенные в два цвета различной интенсивности. Положительная дельта, которая показывает преобладание объёма покупок, окрашивается в зелёный цвет. При этом, чем насыщеннее оттенок, тем сильнее на рынке покупатель. Отрицательная же дельта окрашивается красным, и чем он темнее, тем сильнее на рынке в данный момент продавец. По причине цветовой индикации работа с дельтой ещё называется кластерным анализом.

https://youtube.com/watch?v=Zwh2tXNp1bQ

Этот индикатор расположен внизу графика, под каждым отдельным баром, и в этом случае, он показывает суммарное значение дельты по нему. Также как и на графике Футпринт, тут используется цветовая индикация красным и зелёным цветом.

Итак, вывод очевиден – дельта полезный и нужный трейдеру инструмент, который открывает перед ним большие перспективы профессионального роста. Конечно, оптимальный вариант научиться работать с дельтой – это пройти обучение. Тогда торговля на бирже будет для трейдера ещё проще и интереснее.

Если Вы и дальше хотите читать интересные и доступные статьи о трейдинге, теханализе и финансовых рынках, подписывайтесь на наш блог и получайте свежий контент первыми.

Производная дельта-функции

По определению производной дельта-функции δ(x){\displaystyle \delta (x)}:

∫−∞+∞f(x)δ′(x−a)dx=−f′(a){\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{\prime }(x-a)\,dx=-f^{\prime }(a)}

(распространение интегрирования по частям на случай подынтегральных выражений, содержащих дельта-функцию).

Аналогично для n-й производной дельта-функции:

∫−∞+∞f(x)δn(x−a)dx=−∫−∞+∞∂f∂xδn−1(x−a)dx.{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{}(x-a)\,dx=-\int \limits _{-\infty }^{+\infty }{\frac {\partial f}{\partial x}}\delta ^{}(x-a)\,dx.}

А проинтегрировав так по частям n раз, получим в конце концов:

∫−∞+∞f(x)δn(x−a)dx=(−1)n∂nf(x)∂xn|x=a.{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{}(x-a)\,dx=\left.(-1)^{n}{\frac {\partial ^{n}f(x)}{\partial x^{n}}}\right|_{x=a}.}

Для производной дельта-функции имеет место тождество:

f(x)δ′(x)=f()δ′(x)−f′()δ(x),{\displaystyle f(x)\delta ^{\prime }(x)=f(0)\delta ^{\prime }(x)-f^{\prime }(0)\delta (x),}

которое можно получить дифференцируя произведение f(x)δ(x){\displaystyle f(x)\delta (x)}.

Как работать с Дельтой – внимание к мелочам

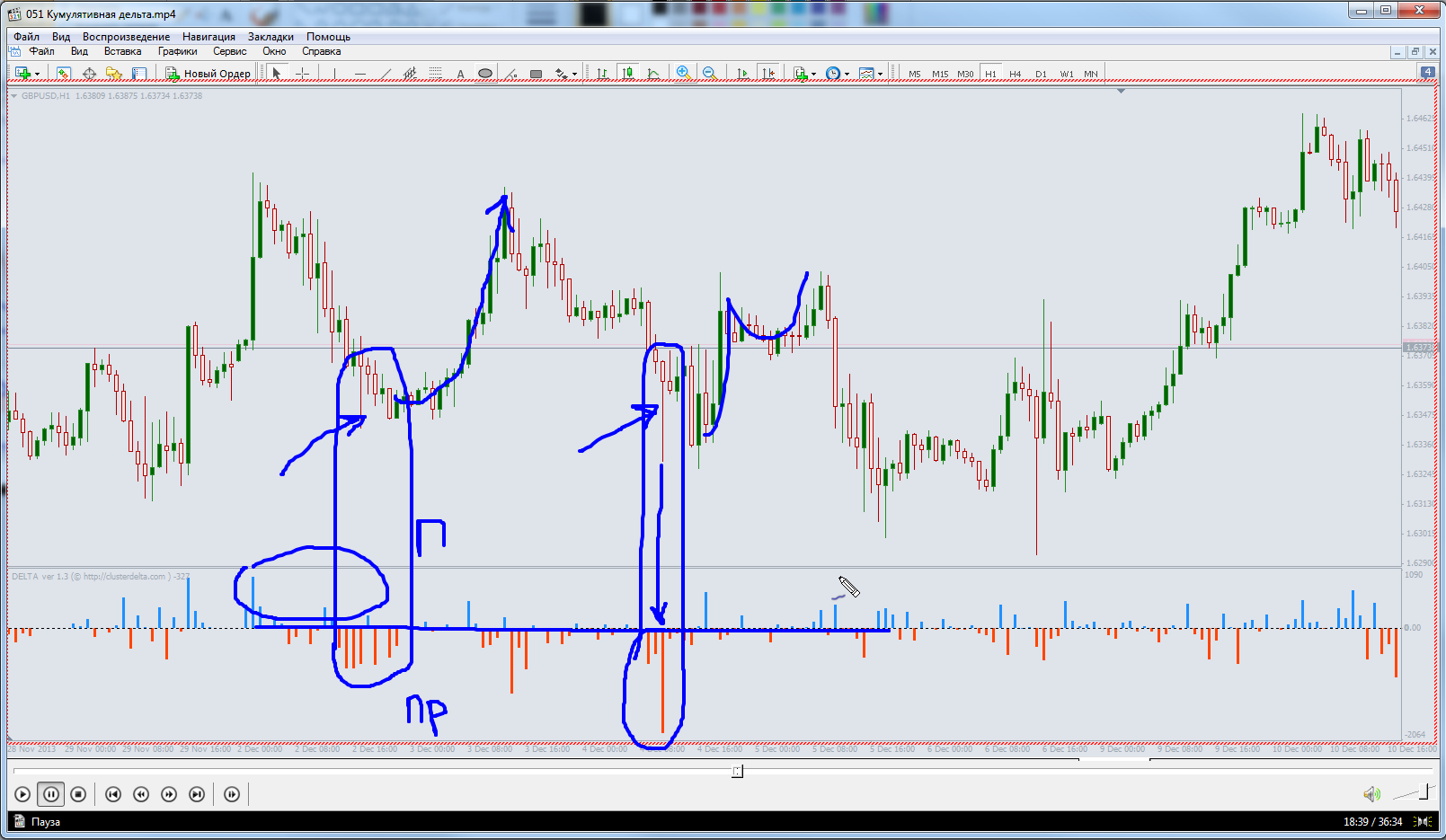
Чтобы получить от этого ценного инструмента максимум пользы, нельзя пренебрегать показателями Дельты во время проведения технического анализа. При этом можно использовать и график Футпринт, и индикатор Дельта на каждом баре, и кумулятивную Дельту, отображающую суммарную Дельту за период времени, например, за торговую сессию.
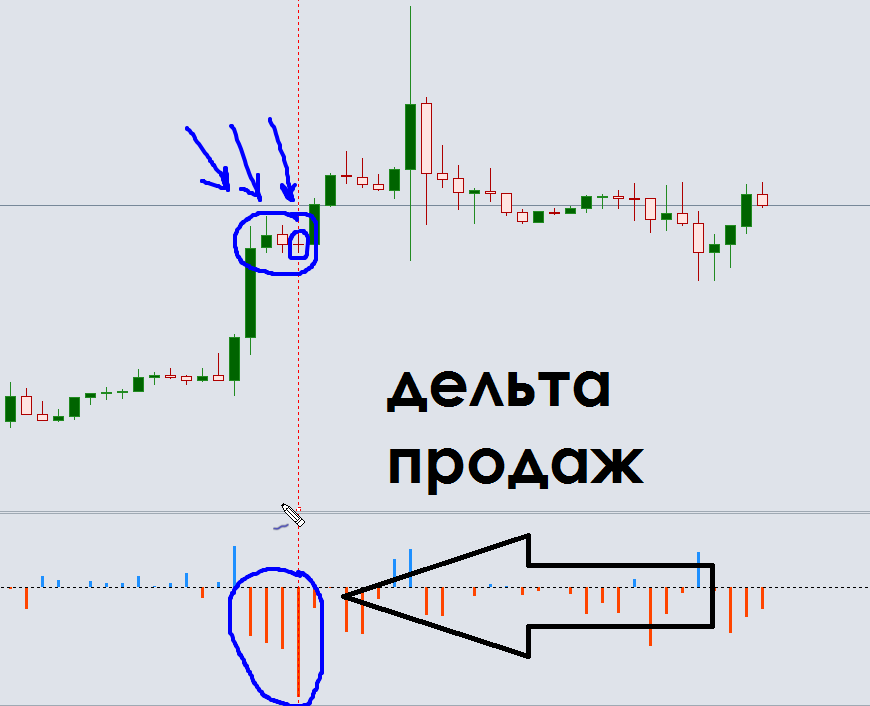
Порой именно показатели Дельты способны дать трейдеру оптимальную точку для входа в рынок. К примеру, по длине отрицательной Дельты можно определить момент окончания периода накопления и войти в сделку прямо перед началом крупного восходящего тренда.

Чтобы научиться, как работать с Дельтой правильно и прибыльно для своей торговли, можно пройти курс в Школе трейдинга Александра Пурнова под руководством опытного наставника. Кроме того, после подписки на наш блог будут доступны ценные материалы на тематику трейдинга и финансов.

ЧТО ТАКОЕ «ДЕЛЬТА»?

Термин Дельта (англ. Delta) вошел в обиход трейдеров в далеком 2002 году, когда был изобретен революционный график Футпринт (англ. Footprint chart). Толчком для этого послужило повсеместное распространение информационных технологий и интернета, затронувшее и сферу трейдинга. Именно тогда доступ к данным о реальных объемах торговли на бирже перестал быть привилегией узкого круга участников рынка, а метод VSA (англ. Volume Spread Analysis — анализ объема и спреда) получил широкое распространение в среде ритейл трейдеров.

Сегодня ритейл трейдер, анализирующий, например, котировки валют Форекс (Forex), благодаря платформе ATAS может подкрепить свои решения торговыми объемами валютных фьючерсов (евро, британского фунта и других). Передовой, интуитивно понятный, а главное ставший доступным каждому, способ визуализации потока ордеров продолжает и по сей день помогать ритейл трейдерам выходить на новый профессиональный уровень.

• Расчет Дельты
• График Футпринт
• ИндикаторDelta
• Кумулятивная Дельта

Начни пользоваться ATAS абсолютно бесплатно! Первые две недели использования платформы дают доступ к полному функционалу с ограничением истории в 7 дней.

δ-Функция как слабый предел

График функции sin⁡xx.{\displaystyle {\frac {\sin x}{x}}.}

Пусть ∫−∞+∞f(x)dx=1.{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\,dx=1.}

Тогда последовательность

fn(x)=nf(nx){\displaystyle f_{n}(x)=nf(nx)}

слабо сходится к δ{\displaystyle \delta }-функции.

Выбор интегрируемой функции f(x),{\displaystyle f(x),} определённый интеграл которой в пределах от −∞{\displaystyle {-\infty }} до +∞{\displaystyle {+\infty }} равен 1 произволен.

Например, в качестве f(x){\displaystyle f(x)} можно выбрать функцию sinc: f(x)=sin⁡πxπx,{\displaystyle f(x)={\frac {\sin \pi x}{\pi x}},}
дающую последовательность:

fn(x)=nsin⁡(nπx)nπx=sin⁡(nπx)πx.{\displaystyle f_{n}(x)=n{\frac {\sin(n\pi x)}{n\pi x}}={\frac {\sin(n\pi x)}{\pi x}}.}

При требовании, чтобы все функции в последовательности были всюду положительны, можно в качестве исходной функции выбрать, например, нормированную функцию Гаусса или иную любую всюду неотрицательную функцию, интеграл которой равен 1:

f(x)=1πe−x2,{\displaystyle f(x)={\frac {1}{\sqrt {\pi }}}e^{-x^{2}},}

fn(x)=nπe−(nx)2.{\displaystyle f_{n}(x)={\frac {n}{\sqrt {\pi }}}e^{-(nx)^{2}}.}

Интегральное представление

Во многих приложениях оказывается удобным интегральное представление дельта-функции:

δ(t)=12π∫−∞+∞eiωtdω.{\displaystyle \delta (t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{+\infty }e^{i\omega t}\,d\omega .}

Доказательство

Рассмотрим интеграл

I(t)=12π∫−∞∞eiωtdω,{\displaystyle I(t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }e^{i\omega t}\,d\omega ,}    (1)

который можно интерпретировать как предел

I(t)=limN→∞IN(t),{\displaystyle I(t)=\lim _{N\to \infty }I_{N}(t),}

где

IN(t)=12π∫−NNeiωtdω=1πNsin⁡tNtN.{\displaystyle I_{N}(t)={\frac {1}{2\pi }}\int \limits _{-N}^{N}e^{i\omega t}\,d\omega ={\frac {1}{\pi }}N{\frac {\sin {tN}}{tN}}.}    (2)

Известно, что

∫−∞∞sin⁡ttdt=π.{\displaystyle \int \limits _{-\infty }^{\infty }{\frac {\sin t}{t}}\,dt=\pi .}    (3)

В силу (3) для любого N{\displaystyle N} справедливо равенство:

∫−∞∞IN(t)dt=1π∫−∞∞sin⁡tNtNd(tN)=1.{\displaystyle \int \limits _{-\infty }^{\infty }I_{N}(t)\,dt={\frac {1}{\pi }}\int \limits _{-\infty }^{\infty }{\frac {\sin {tN}}{tN}}\,d(tN)=1.}    (4)

Можно показать (), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к δ(t).{\displaystyle \delta (t).}

Представление многомерных дельта-функций в различных системах координат

В n-мерном пространстве в декартовых координатах (ортонормированном базисе):

∫δn(x1,x2,…,xn)dnx=1;{\displaystyle \int \delta ^{n}(x_{1},\;x_{2},\;\ldots ,\;x_{n})\,d^{n}x=1;}

δn(x1,x2,…,xn)=δ(x1)δ(x2)…δ(xn).{\displaystyle \delta ^{n}(x_{1},\;x_{2},\;\ldots ,\;x_{n})=\delta (x_{1})\delta (x_{2})\ldots \delta (x_{n}).}

В двумерном пространстве:

∬−∞+∞δ2(x,y)dxdy=1;{\displaystyle \iint \limits _{-\infty }^{+\infty }\delta ^{2}(x,\;y)\,dx\,dy=1;}

δ2(ax,by)=1|ab|δ2(x,y);{\displaystyle \delta ^{2}(ax,\;by)={\frac {1}{\left|ab\right|}}\delta ^{2}(x,\;y);}

δ2(x,y)=δ(x)δ(y).{\displaystyle \delta ^{2}(x,\;y)=\delta (x)\delta (y).}

В полярных координатах:

δ2(r,φ)=δ(r)2π|r|{\displaystyle \delta ^{2}(r,\;\varphi )={\frac {\delta (r)}{2\pi \left|r\right|}}} — несмещённая относительно начала координат (с особенностью при r=0),

δ(r−r)δ(φ−φ)|r|{\displaystyle {\frac {\delta (r-r_{0})\delta (\varphi -\varphi _{0})}{|r|}}} — с особенностью в точке общего положения (r,φ);{\displaystyle (r_{0},\;\varphi _{0});} при r=0 доопределяется нулём.

В трёхмерном пространстве:

∭−∞+∞δ3(x,y,z)dxdydz=1;{\displaystyle \iiint \limits _{-\infty }^{+\infty }\delta ^{3}(x,\;y,\;z)\,dx\,dy\,dz=1;}

δ3(x,y,z)=δ(x)δ(y)δ(z).{\displaystyle \delta ^{3}(x,\;y,\;z)=\delta (x)\delta (y)\delta (z).}

В цилиндрической системе координат:

δ3(r,θ,z)=δ(r)δ(z)2πr{\displaystyle \delta ^{3}(r,\;\theta ,\;z)={\frac {\delta (r)\delta (z)}{2\pi r}}} — несмещённая относительно начала координат (с особенностью при r=,z={\displaystyle r=0,\;z=0}),

δ(r−r)δ(φ−φ)δ(z−z)|r|{\displaystyle {\frac {\delta (r-r_{0})\delta (\varphi -\varphi _{0})\delta (z-z_{0})}{|r|}}} — с особенностью в точке общего положения (r,φ,z);{\displaystyle (r_{0},\;\varphi _{0},\;z_{0});} при r=0 доопределяется нулём.

В сферической системе координат:

δ3(r,θ,φ)=δ(r)4πr2{\displaystyle \delta ^{3}(r,\;\theta ,\;\varphi )={\frac {\delta (r)}{4\pi r^{2}}}} — несмещённая относительно начала координат (с особенностью при r=0).

В формулах с особенностью в начале координат нередко используют вдвое большие коэффициенты (1/π для цилиндрической и полярной, 1/2π для сферической). Это связано с тем, что предполагается вдвое меньший результат интегрирования в случае, если особая точка находится точно на границе интервала интегрирования.

Кумулятивная Дельта

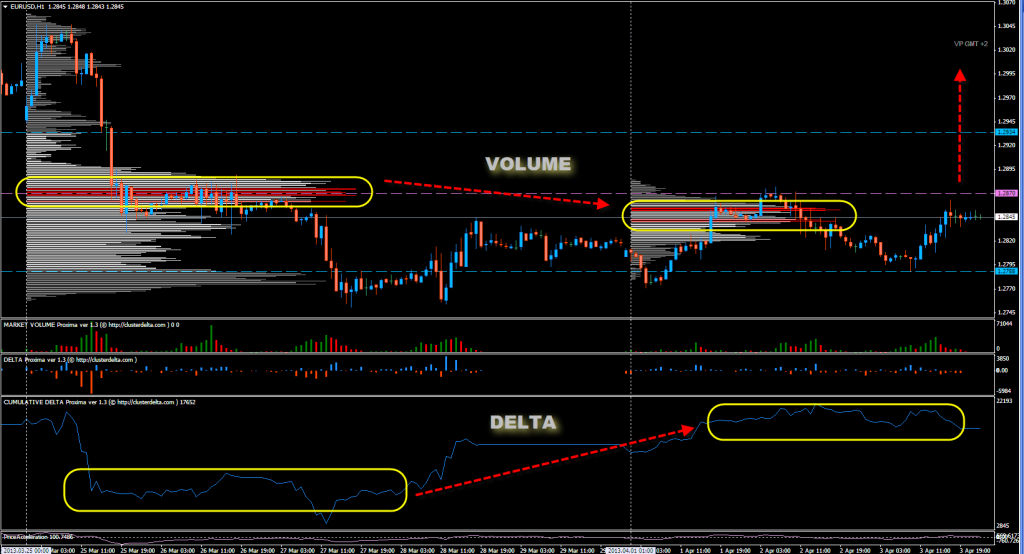
Кумулятивная Дельта (англ. Cumulative Delta) — это накопительная дельта за определенный промежуток времени. Если обычная Дельта, которую мы рассматривали выше, показывает разницу между рыночными покупками и продажами для каждой свечи/бара, то кумулятивная Дельта отображает полную динамику баланса рыночных покупок и продаж начиная с определенного момента времени (с начала торговой сессии или контракта).

Таким образом кумулятивная Дельта позволяет увидеть более широкую картину Дельты, так как она может охватывать торговую сессию или же целый день. Поэтому не имеет значения какой фрейм или период вы используете для построения графика. Индикатор Cumulative Delta платформы ATAS подсчитывает накопительную Дельту и отображает ее текущий итоговый показатель в нижней части графика.

Помимо этого, показатель кумулятивной Дельты, как и другие подробные цифровые показатели Дельты можно вывести на график при помощи индикатора Cluster Statistic. В нем показатели кумулятивной Дельты будут выводиться в строке Session Delta.

Кумулятивная Дельта, может быть как положительной, так и отрицательной. Положительная кумулятивная Дельта окрашивается в зеленый цвет и характеризует «положительный» поток ордеров за торговую сессию, как результат более агрессивного поведения покупателей. Отрицательная кумулятивная Дельта окрашивается в красный цвет и характеризует «отрицательный» поток ордеров за торговую сессию, как результат более «агрессивного» поведения продавцов.

График №4. 5-минутный таймфрейм фьючерса на нефть Light Sweet Crude Oil (тикер CL). График Футпринт Bid x Ask и индикаторы Cumulative Delta и Cluster Statistic в нижней части графика

В заключении статьи следует отметить, что Дельту, несмотря на все ее сильные стороны, следует использовать лишь в связке с другими торговыми элементами вашей торговой стратегии.