Экспоненциальный рост
Пи — это бесконечное число, поэтому люди по определению не смогут никогда установить точные цифры этого числа. Однако количество цифр после запятой сильно увеличилось со времен первого использования Пи. Еще вавилоняне им пользовались, но им было достаточно дроби в три целых и одну восьмую. Китайцы и создатели Ветхого Завета и вовсе ограничивались тройкой. К 1665 году сэр Исаак Ньютон вычислил 16 цифр Пи. К 1719 году французский математик Том Фанте де Ланьи вычислил 127 цифр. Появление компьютеров радикальным образом улучшило знания человека о Пи. С 1949 года по 1967-й количество известных человеку цифр стремительно выросло с 2037 до 500 000. Не так давно Петер Труэб, ученый из Швейцарии, смог вычислить 2,24 триллиона цифр Пи! На это потребовалось 105 дней. Разумеется, это не предел. Вполне вероятно, что с развитием технологий будет возможно установить еще более точную цифру — так как Пи бесконечно, предела точности просто не существует, и ограничить ее могут лишь технические особенности вычислительной техники.
Для моего пирога нужны цельные половинки груш, покрытые карамелью: рецепт
Мы кормили бесплатно друзей каждую неделю и не ожидали от них такой наглости
«Тяжелый фильм»: как россияне отреагировали на показ сериала «Ненастье»
Нормальное ли число Пи?
Число Пи определенно странное, но насколько оно подчиняется нормальным математическим законам? Ученые уже разрешили многие вопросы, связанные с этим иррациональным числом, но некоторые загадки остаются. К примеру, неизвестно, насколько часто используются все цифры – цифры от 0 до 9 должны использоваться в равной пропорции. Впрочем, по первым триллионам цифр статистика прослеживается, но из-за того, что число бесконечное, доказать точно ничего невозможно. Есть и другие проблемы, которые пока ускользают от ученых. Вполне возможно, что дальнейшее развитие науки поможет пролить на них свет, но на данный момент это остается за пределами человеческого интеллекта.
Последовательность Фибоначчи и вычисление числа Пи
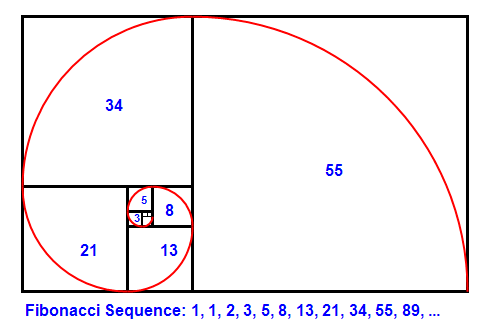
Долгое время вычисления числа Пи основывались на двух методах: первый был разработан Архимедом, а второй был разработан Джеймсом Грегори, шотландским математиком в 1671 году. Однако оказывается, что последовательность Фибоначчи также может быть эффективно использована для вычисления значение Пи.
Последовательность Фибоначчи — это числовая последовательность, в которой число создается или определяется путем добавления двух чисел перед ним. Последовательность начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и продолжается бесконечно. Поскольку арктангенс 1 равен Пи / 4, переставляя уравнение в arctan (1) * 4 = Пи, мы также можем продемонстрировать Пи в терминах чисел Фибоначчи.
Тайны числа Пи
В романе Карла Сагана «Контакт», по которому снят одноименный фильм, инопланетяне сообщают героине, что среди знаков Пи содержится тайное послание от Бога. С некоторой позиции цифры в числе перестают быть случайными и представляют себе код, в котором записаны все секреты Мироздания.
Этот роман на самом деле отразил загадку, занимающую умы математиков всей планеты: является ли число Пи нормальным числом, в котором цифры разбросаны с одинаковой частотой, или с этим числом что-то не так. И хотя ученые склоняются к первому варианту (но не могут доказать), число Пи выглядит очень загадочно. Один японец как то подсчитал, сколько раз встречаются числа от 0 до 9 в первом триллионе знаков Пи. И увидел, что числа 2, 4 и 8 встречаются чаще, чем остальные. Это может быть одним из намеков на то, что Пи не совсем нормальное, и цифры в нем действительно не случайны.
Вспомним всё, что мы прочли выше, и спросим себя, какое еще иррациональное и трансцендентное число так часто встречается в реальном мире?
А в запасе имеются еще странности. Например, сумма первых двадцати цифр Пи равна 20, а сумма первых 144 цифр равна «числу зверя» 666.

Нам известно также, что число Пи содержит последовательность 0123456789, но находится она на 17 387 594 880-й цифре.
Все это означает, что в бесконечности числа Пи можно обнаружить не только интересные сочетания цифр, но и закодированный текст «Войны и Мира», Библии и даже Главную Тайну Мироздания, если таковая существует.
Кстати, о Библии. Известный популяризатор математики Мартин Гарднер в 1966 году заявил, что миллионным знаком числа Пи (на тот момент еще неизвестным) будет число 5. Свои расчеты он объяснил тем, что в англоязычной версии Библии, в 3-й книге, 14-й главе, 16-м стихе (3-14-16) седьмое слово содержит пять букв. Миллионную цифру получили спустя восемь лет. Это было число пять.
Стоит ли после этого утверждать, что число Пи случайно?
Количество знаков
Примерно в то же время подтянулись и другие менее известные математики, предложившие новые формулы расчета числа Пи через тригонометрические функции.
Например, вот по какой формуле рассчитывал Пи преподаватель астрономии Джон Мэчин в 1706 году: PI / 4 = 4arctg(1/5) – arctg(1/239). С помощью методов анализа Мэчин вывел из этой формулы число Пи с сотней знаков после запятой.
До эры компьютеров математики занимались тем, чтобы рассчитать как можно больше знаков. В связи с этим порой возникали курьезы. Математик-любитель У. Шенкс в 1875 году рассчитал 707 знаков числа Пи. Эти семь сотен знаков увековечили на стене Дворца Открытий в Париже в 1937 году. Однако спустя девять лет наблюдательными математиками было обнаружено, что правильно вычислены лишь первые 527 знаков. Музею пришлось понести приличные расходы, чтобы исправить ошибку – сейчас все цифры верные.
Когда появились компьютеры, количество цифр числа Пи стало исчисляться совершенно невообразимыми порядками.
По мере совершенствования компьютеров наше знание числа Пи все дальше и дальше уходило в бесконечность. В 1958 году было рассчитано 10 тысяч знаков числа. В 1987 году японцы высчитали 10 013 395 знаков. В 2011 японский исследователь Сигеру Хондо превысил рубеж в 10 триллионов знаков.
Вычисление Пи вручную
Если вы хотите найти число самостоятельно, вы можете использовать старомодную технику – вам потребуются линейка, банка и веревка, можно также использовать транспортир и карандаш. Минус использования банки в том, что она должна быть круглой, и точность будет определяться тем, насколько хорошо человек может наматывать веревку вокруг нее. Можно нарисовать окружность транспортиром, но и это требует навыков и точности, так как неровная окружность может серьезно исказить ваши измерения. Более точный метод предполагает использование геометрии. Разделите круг на множество сегментов, как пиццу на кусочки, а потом вычислите длину прямой линии, которая превратила бы каждый сегмент в равнобедренный треугольник. Сумма сторон даст приблизительное число Пи. Чем больше сегментов вы используете, тем более точным получится число. Разумеется, в своих вычислениях вы не сможете приблизиться к результатам компьютера, тем не менее эти простые опыты позволяют более детально понять, что вообще представляет собой число Пи и каким образом оно используется в математике.
Странные тенденции соцсети: причудливые изображения статуй, «борющихся» с людьми
Из труб ПВХ, остатков плитки и цемента можно сделать оригинальный столик
Экологичный летний пудинг: вкусно и без отходов
Скрытая связь между квантовой механикой и Пи

Физики недавно обнаружили связь между многовековой известной математической формулой Пи и квантовой механики, которая скрывалась годами. Это было в 1665 году, когда известный британский математик Джон Уоллис представил свою собственную версию формулы вычисления Пи. Исследователи из Университета Рочестера считают, что они нашли ту же формулу, скрывающуюся при расчете энергетических уровней атома водорода.
Краткие факты

С 1998 года, каждый год 14 марта, научное сообщество празднует день Пи. Этот конкретный день был выбран из-за его соответствия с 3.14, который является пи значение. Первое широко посещаемое празднование дня пи было организовано физиком Ларри Шоу. Интересно, что Альберт Эйнштейн родился 14 марта 1879 года.
В 2002 году группа японских исследователей из Токийского университета вычислила 1,24 триллиона цифр числа пи, используя мощный суперкомпьютер Hitachi SR 8000, побив все предыдущие рекорды.
По мнению некоторых математиков, вместо того чтобы называть его Безугловым, гораздо правильнее сказать, что круг имеет бесконечное число углов.
Проблема с лентой
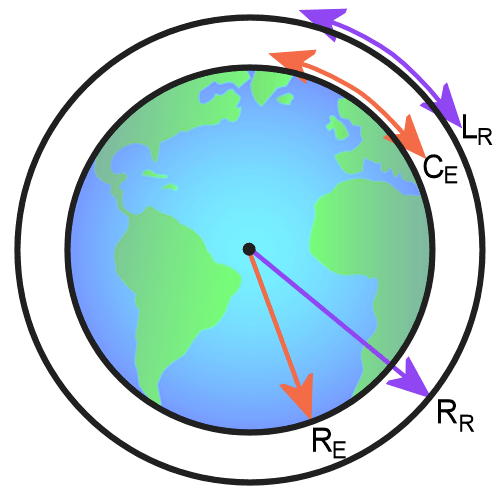
Предположим, вы хотите обернуть вокруг Земли ленту на экваторе, длина окружности которого составляет 24 900 миль (идеальная сфера). Теперь попытайтесь выяснить, сколько потребуется ленты, которая могла бы окружить Землю на расстоянии одного дюйма над ее поверхностью. Можно легко подумать, что для этого потребуется огромное количество ленты. Но на самом деле это не так. Мы расскажем вам, как.
Еще раз предположив, что Земля является идеальной сферой, у нас будет круг с окружностью 24 900 миль (на экваторе). Это означает, что радиус будет 24 900 / (2 * пи) или примерно 3963 миль. Теперь вторая лента, на дюйм выше поверхности Земли, будет иметь радиус на один дюйм больше радиуса Земли, что дает нам уравнение C = 2 Пи (r + 1) или C = 2 Пи (r) + 2 Пи.
Отсюда можно сказать, что окружность второй ленты увеличится на 2Пи. Фактически, независимо от того, какой первоначальный радиус увеличивает радиус, всегда будет 2Пи.
Распределение вероятностей
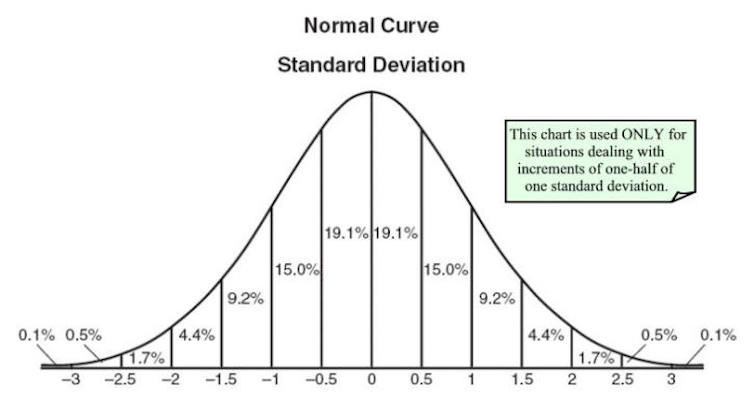
Пи также играет важную роль в нормальном распределении вероятностей. Без сомнения, вы сталкивались с таким распределением вероятностей не один, а много раз. Они важны и часто используются в различных областях исследований, включая математику, физику и общественные науки. Это то, что вам нужно, от прогнозирования результатов теста ученика до измерения отдаленных сверхновых звезд.
Это правило большого пальца: всякий раз, когда вы видите, как Пи подкрадывается где-то в любом уравнении, убедитесь, что где-то в этом спрятан круг. В этом случае Пи вводится через интеграл Эйлера – Пуассона, который содержит квадратный корень из Пи.
Открытие Эйлера
Знаменитый немецкий, швейцарский и российский ученый Леонард Эйлер (1707-1783) внес решающий вклад в понимание арифметической природы числа π. Он сумел определить последовательный ряд для его вычисления. Если взять 210 членов подобного ряда можно получить 100 правильных знаков π. Самому Эйлеру удалось определить значение константы с точностью 153 десятичных знака.
Интересный факт: π считается трансцендентным — не существует алгебраической формулы, выражающей π через рациональные числа.
Леонард Эйлер
Массово использовать символ π начали примерно с 1736 года после того, как Эйлер стал неоднократно употреблять его в своих работах. Среди них были труды, где приведено множество утверждений, связанных с количеством суммируемых членов, которые требуются для определения приближенного показателя «пи» с заданной точностью.
Интересный факт: существует пи-клуб, участники которого знают на память тысячи знаков числа.
Интерес к числу «пи» люди проявили еще в древности, когда начали вычислять его значение. Однако до XVIII века оно не имело общепринятого наименования. Величиной без имени математическая константа перестала быть благодаря двум математикам У. Джонсу и Л. Эйлеру. Первый предложил символ π, а второй придал ему широкое распространение.
Свойства[править]
Соотношенияправить
Известно много формул с числом \(\pi\):
Франсуа Виет, 1593:
$$\frac{2}{\pi}=\sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2} \sqrt{\frac{1}{2}}}} \, \cdot \ldots$$
Формула Валлиса:
$$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2} $$
Формула Валлиса-Александрова:
$$ \frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \left \cdots = \frac{\pi}{2}$$
Модифицированная формула Валлиса:
$$\lim \limits_{m\rightarrow \infty }{\frac { (m!)^{4}{2}^{4m}}{\left ^{2}m}} = \pi$$
Произведения:
$$\pi=3\cdot \frac{\sqrt{3}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{1}{3}\right )^2}$$
$$\pi=\frac{3}{2}\cdot \frac{\sqrt{3}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{2}{3}\right )^2}$$
$$\pi=4\cdot \frac{\sqrt{2}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{1}{4}\right )^2}$$
$$\pi=\frac{4}{3}\cdot \frac{\sqrt{2}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{3}{4}\right )^2}$$
$$\pi=6\cdot \frac{1}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{1}{6}\right )^2}$$
$$\pi=\frac{6}{5}\cdot \frac{1}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{5}{6}\right )^2}$$
$$\pi=4\cdot\prod \limits_{k=1}^{\infty}\frac{k^2+k}{k^2+k+\frac{1}{4}}$$
$$\pi=\frac{9}{2}\cdot\frac{\sqrt{3}}{2}\prod \limits_{k=1}^{\infty} \frac{k^2+k}{k^2+k+ \frac{2}{9}}$$
$$\pi=\frac{16}{3}\cdot\frac{\sqrt{2}}{2}\prod \limits_{k=1}^{\infty} \frac{k^2+k}{k^2+k+ \frac{3}{16}}$$
$$\pi=\frac{36}{5}\cdot\frac{1}{2}\prod \limits_{k=1}^{\infty} \frac{k^2+k}{k^2+k+ \frac{5}{36}}$$
$$\pi= 2\sqrt{3}\prod \limits_{k=1}^{\infty}\frac{\left ( 2k-1 \right )^{\frac 12 -k} \left ( 2k+3 \right )^{k+\frac 12}}{2k+1}\left (\frac{k}{k+1} \right )^{2k}$$
Ряд Лейбница:
$$\frac{1}{1} — \frac{1}{3} + \frac{1}{5} — \frac{1}{7} + \frac{1}{9} — \cdots = \frac{\pi}{4}$$
Тождество Эйлера:
$$e^{i \pi} + 1 = 0\;$$
Т. н. «интеграл Пуассона» или «интеграл Гаусса»
$$\int\limits_{-\infty}^{+\infty}\ e^{-x^2}{dx} = \sqrt{\pi}$$
Интегральный синус
$$\int\limits_{-\infty }^{+\infty }{\frac{\sin(x)}{x}dx}=\pi $$
Интегральный косинус
$$\int\limits_{-\infty }^{+\infty }{\frac{1-\cos(x)}{x^2}dx}=\pi $$
Интегральный тангенс
$$\int\limits_{-\infty }^{+\infty }{\frac{tg(x)}{x}dx}=\pi $$
Интегральный котангенс
$$\int\limits_{-\infty }^{+\infty }{\frac{1-x \cdot ctg(x)}{x^2}dx}=\pi $$
Интегральный арктангенс
$$2 \int \limits _{-\infty }^{\infty }\! \frac {x-arctg(x)}{x^3}{dx}=\pi $$
Трансцендентность и иррациональностьправить
- Иррациональность числа \(\pi\) была впервые доказана Иоганном Ламбертом в 1767 году путём разложения числа \(\frac{e-1}{2^n}\) в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел \(\pi\) и \(\pi^2\).
- В 1882 годe профессору Кёнигсбергского, а позже Мюнхенского университета Фердинанду Линдеману удалось доказать трансцендентность числа \(\pi\). Доказательство упростил Феликс Клейн в 1894 году
Поскольку в геометрии Евклида площадь круга и длина окружности являются функциями числа \(\pi\), то доказательство трансцендентности \(\pi\) положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.
Новый взгляд на Пи
Еще до того, как число Пи стали соотносить с окружностями, у математиков уже было множество способов даже для наименования этого числа. К примеру, в старинных учебниках по математике можно найти фразу на латыни, которую можно грубо перевести как «количество, которое показывает длину, когда на него умножается диаметр». Иррациональное число прославилось тогда, когда швейцарский ученый Леонард Эйлер использовал его в своих трудах по тригонометрии в 1737 году. Тем не менее греческий символ для Пи все еще не использовали – это произошло только в книге менее известного математика Уильяма Джонса. Он использовал его уже в 1706 году, но это долго оставалось без внимания. Со временем ученые приняли такое наименование, и теперь это наиболее известная версия названия, хотя прежде его называли также лудольфовым числом.
Смачиваю ткань в растворе, добавляю воздушные шарики: бетонные горшки делаю сама
Булочки со сливочным сыром и вишней: ароматная выпечка а-ля чизкейк
Я люблю абрикосовый джем, а муж — клубничный. Поэтому делю торт на ромбики
Оценки[править]
- \(\frac{22}{7}\) (Архимед),
- \(\frac{377}{120}\) (дана в книге индийского мыслителя и астронома Арьябхаты в V веке н. э.),
- \(\frac{355}{113}\) (оценка приписывается современнику Арьябхаты древнекитайскому астроному Цзу Чун-цжи).
- \(\pi\, \approx \,\frac{63}{25}\cdot \frac{17+15 \sqrt{5}}{7+15\sqrt{5}}\) (приближение дал великий индийский математик С.Рамануджан)
- 510 знаков после запятой:
- π ≈ 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362…
- Двести миллиардов знаков после запятой (2000 ZIP архивов, средний размер файла около 57 мегабайт)
Примечания[править]
- Это определение пригодно только для евклидовой геометрии. В других геометриях отношение длины окружности к длине её диаметра может быть произвольным. Например, в геометрии Лобачевского это отношение меньше, чем \(\pi~\).
- Brent, Richard (1975), Traub, J F, ed., «Multiple-precision zero-finding methods and the complexity of elementary function evaluation», Analytic Computational Complexity (New York: Academic Press): 151–176, retrieved 2007-09-08
- Jonathan M Borwein Pi: A Source Book. — Springer, 2004. — ISBN о книге
- ↑ Bailey, David H., Borwein, Peter B., and Plouffe, Simon (April 1997). «On the Rapid Computation of Various Polylogarithmic Constants» (PDF). Mathematics of Computation 66 (218): 903–913. DOI:10.1090/S0025-5718-97-00856-9.
- Bellard, Fabrice. «A new formula to compute the nth binary digit of pi». Archived from the original on 2007-03-09. Retrieved 2007-10-27.
- Plouffe, Simon. «Indentities inspired by Ramanujan’s Notebooks (part 2)» (PDF). Retrieved 2009-4-10.
- Установлен новый рекорд точности вычисления числа π
- Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году
- Г. А. Гальперин. Биллиардная динамическая система для числа пи.
- Профессор Андрей Слюсарчук установил мировой рекорд по возможностям человеческой памяти http://www.mk.ru/health/303812.html?phrase_id=1446233
- Президент поздравил профессора Андрея Слюсарчука с установлением нового мирового рекорда по запоминанию и воспроизведению человеком сверхбольшого объема информации http://www.president.gov.ua/ru/news/14234.html
- Ющенко привітав Слюсарчука зі світовим рекордом із запам’ятовування надвеликого обсягу інформації http://news.liga.net/ukr/news/NU094415.html
- Книга рекордов Украины http://www.book.adamant.ua/akt/2slysar4uk/1.htm
- «Japanese man recites pi from memory to 100,000 decimal places, claims world record». The Associated Press. 04/10/06. Archived from the original on 2013-01-03. Retrieved 22 сентября 2008.
- The Indiana Pi Bill, 1897
- В. И. Арнольд любит приводить этот факт, см. например здесь (ps)
История вычисления константы пи
Ещё в третьем тысячелетии до нашей эры учёные из Древнего Египта, Месопатамии, Индии и Греции замечали, что соотношение длины и диаметра окружности всегда чуть больше трёх независимо от размеров окружности.
Изучение пи в древней Европе
В Месопотамии это соотношение считали равным трём. В Индии отношение длины к диаметру окружности приравнивали к квадратному корню из десяти. Первым математиком, предложившим доказательный метод расчёта пи, был Архимед. Его способ был прост и нагляден. Архимед вписывал в окружность с диаметром в единицу равносторонние многоугольники и описывал такие же многоугольники вокруг окружности, а потом вычислял периметры этих многоугольников. Таким образом, он получал границы для оценки длины окружности: периметр вписанного многоугольника ограничивал длину окружности снизу, а периметр описанного многоугольника — сверху.
Увеличивая количество углов в многоугольниках, Архимед повышал точность своей оценки. Когда он дошёл до 96 углов в многоугольнике, расчётное значение длины окружности оказалось больше, чем 3+10/71, но меньше, чем 3+1/7. Тогда Архимед выбрал верхнюю границу в качестве приблизительного значения константы пи. Согласно этому предположению, число пи равно 22/7 или 3,142857, если представить его в виде десятичной дроби. То есть, Архимед приблизился к числу пи с точностью до второго знака.
Во втором веке нашей эры дело Архимеда продолжил Клавдий Птолемей. Он довёл количество углов в многоугольнике до 720 и получил приблизительное значение числа пи 377/120 или 3,14166667. Клавдию Птолемею удалось высчитать константу пи с точностью до третьей цифры после запятой.
В шестнадцатом веке нашей эры математик из Голландии Лудольф ван Цейлен потратил десять лет на удваивание углов многоугольника и высчитал константу пи с точностью до двадцати знаков после запятой. Он завещал, чтобы найденные им цифры были выбиты на его надгробной плите. А саму константу стали называть числом Лудольфа.
Изучение числа пи в древнем Китае
Наряду с европейскими математиками, число пи пытались рассчитать и в Поднебесной. В третьем веке нашей эры математик из Китая Лю Хуэй вывел алгоритм, для расчёта константы пи с любой возможной степенью точности. В основу алгоритма легла всё та же идея Архимеда. По такому алгоритму самим Лю Хуэем было высчитано приближение пи для многоугольника с 3072 углами. Оно получилось равным 3,14159. Точность возросла до пятого знака после запятой. В пятом веке нашей эры математик Цзу Чунчжи Вычислил пи с точностью до семи цифр после запятой, расположив эту константу между 3,1415926 и 3,1415927.
Число пи: от средневековья до наших дней
В связи с развитием математического анализа во втором тысячелетии нашей эры для нахождения значения числа пи стали использоваться математические ряды:
- Ряд Мадхавы-Лейбница сходился медленно, но после некоторых преобразований позволил вычислить константу пи с точностью до одиннадцати цифр после запятой.
- Формула Виета — первая точная математическая формула для нахождения числа пи — представляет собой бесконечное произведение.
- Формула Валлиса также представляет собой произведение для расчёта константы пи по аналогии с константой е.
- Формула Джона Мэчина имеет в своей основе разложение арктангенса в Ряд Тейлора.
- Бесконечный ряд обратных квадратов, как доказал Эйлер сходится к квадрату пи, деленному на шесть.
Теория вероятностей тоже внесла свой вклад в вычисление пи с помощью метода Монте-Карло и Иглы Бюффона. Но с появлением компьютеров, а также открытием преобразования Фурье, использование рядов для вычисления значения пи позволило достигать астрономической точности.
Самый первый расчет

Считается, что Пи был первоначально открыт древними вавилонянами около 4000 лет назад. Согласно Rhind Papyrus, древние египтяне вычислили значение Пи как приблизительно 3.1605. Но первый зарегистрированный метод для вычисления значения числа Пи был разработан греческим математиком Архимедом Сиракузским в 250 году до нашей эры.
Архимед грубо рассчитал площадь круга, найдя области двух отдельных многоугольников правильного размера. Один был вписан в круг, а другой-внутри того круга, в котором он был очерчен. Таким образом, два полигона обеспечивали верхнюю и нижнюю границы площади круга (фактическая площадь круга лежит между областями вписанных и описанных многоугольников).
Архимед знал о том факте, что он не обнаружил фактическое значение Пи, а лишь приблизительное значение в этих пределах. Таким образом, Архимед показал, что число Пи между 3 1/7 и 3 10/71. Этот алгоритм строго использовался учеными и инженерами на протяжении 1000 лет, из-за чего даже сегодня его иногда называют «постоянной Архимеда».
Запоминание Пи
Рекорд в запоминании цифр после запятой принадлежит Раджвиру Мине из Индии, которому удалось запомнить 70 000 цифр – он поставил рекорд двадцать первого марта 2015 года. До этого рекордсменом был Чао Лу из Китая, которому удалось запомнить 67 890 цифр – этот рекорд был поставлен в 2005-м. Неофициальным рекордсменом является Акира Харагучи, записавший на видео свое повторение 100 000 цифр в 2005-м и не так давно опубликовавший видео, где ему удается вспомнить 117 000 цифр. Официальным рекорд стал бы только в том случае, если бы это видео было записано в присутствии представителя книги рекордов Гиннеса, а без подтверждения он остается лишь впечатляющим фактом, но не считается достижением. Энтузиасты математики любят заучивать цифру Пи. Многие люди используют различные мнемонические техники, к примеру стихи, где количество букв в каждом слове совпадает с цифрами Пи. В каждом языке существуют свои варианты подобных фраз, которые помогают запомнить как первые несколько цифр, так и целую сотню.
Олег Табаков и настоящий Шелленберг: удивилась, насколько они похожи (фото)
О работе и детях: три коротких анекдота, которые подойдут для любой компании
Беспокойство? Избавиться от него помогут предметы синего цвета
Игла Буффона
Игла Буффона или просто проблема с иглой в вероятности была впервые указана Жоржем-Луи Леклерком, графом де Буффоном, в 18-м веке, когда падение иглы на лист, отмеченный линиями, определит вероятность того, что игла пересечет линию на странице
Важно отметить, что вероятность результата эквивалентна значению числа Пи
Давайте разберемся с этим. В этом случае на самом деле есть две переменные: угол наклона иглы, давайте присвоим ему символ тета (θ) и расстояние между ближайшей линией и центральной точкой иглы. Тета может варьироваться от 0 ° до 180 °, который измеряется параллельно нарисованным линиям.
Выяснилось, что вероятность того, что игла прорежет линию при посадке, составляет ровно 2 / Пи или почти 64%. Это означает, что число Пи можно как-то рассчитать, используя технику Буффона, если у кого-то будет достаточно времени и терпения, чтобы пройти все симуляции. Чтобы понять это намного лучше, вы можете попробовать это.
Преобразование Фурье и обработка сигналов

Пи играет еще одну очень важную роль в области «обработки сигналов». Это просто анализ, синтез и модификация сигналов. Но здесь действует сложная система. Эта сложная система представляет собой «преобразование Фурье», которое преобразует сигналы в частотный спектр. Мобильный телефон каждого, будь то его андроид или iPhone, выполняет преобразование Фурье, когда он связывается с местной сотовой вышкой.
Кроме того, формула оценивается вашим мобильным телефоном в цифровом виде с помощью определенного алгоритма, известного как «быстрое преобразование Фурье» или «БПФ», который был открыт математиками в 1950-х годах
Важно отметить, что каждый процесс включает в себя число π. Так что технически, есть определенное значение Пи где-то в вашем телефоне, будь то простой или смартфон
А если бы мы не знали Пи?
Путешествия на автомобиле
Для начала пи позволяет нам точно рассчитывать и создавать окружности. Представьте, что колёса вашей машины немного отличаются друг от друга, каждое слегка смещено от центра. Вы не только будете постоянно тратить кучу денег на механика, но и поездки у вас также будут менее удобными.
Путешествия по воздуху
Пи играет важную роль в расчёте времени и расстояния путешествия на самолёте. Когда самолёты летают на большие расстояния, они летят по округлой дуге потому что, Земля круглая.
Казино
Всеми любимая формула нормального распределения (также называемая распределением Гаусса) считается с помощью пи. Проще говоря: пи играет ключевую роль в формулах по теории вероятности и статистике — поэтому с пи азартные игры становятся намного более предсказуемыми. И с этими расчётами люди открывают казино, зная наверняка, какой процент их клиентов будет выигрывать и проигрывать.
Идея Уильяма Джонса
Удивительно, но знаменитое число до XVIII века не имело постоянного названия. В Средневековье его нередко называли «число, которое при умножении на него диаметра позволяет получить длину окружности». Еще одно наименование — «людольфово число» было дано в честь голландского ученого Людольфа ван Цейлена (1540-1610), сумевшего определить значение постоянной с точностью до 20 десятичных цифр. Также использовались числовые обозначения 355/113 и 22/7, что формировало иллюзию о рациональности числа.
 Математик Уильям Джонс
Математик Уильям Джонс
Все изменилось, когда английский математик Уильям Джонс (1675-1749) в 1706 году опубликовал работу «Обозрение достижений математики», в котором использовал греческую букву π для ныне самой известной математической константы. Он руководствовался простой логикой — с буквы «пи» начинается слово περιμετρέ, что означает «измеряю вокруг».
Интересный факт: число π имеет свой день рождения — 14 марта.
Уильям Джонс использует греческую букву π
Интересный факт: π обладает собственным языком — в нем количество букв в словах тождественно цифрам числа «пи» в последовательном порядке.
Однако существует мнение, что Джонс ранее видел символ π. Его коллега Уильям Отред (1575-1660) с помощью буквы «пи» обозначал длину конкретной окружности, поэтому величина постоянно менялась. После жизни Отреда ряд его трудов и документов попали к Джонсу, который придал π философский смысл. Но широкое распространение символ π получил благодаря другому, гораздо более известному математику.
История появления числа «Пи»
Постоянство отношения длины окружности к ее диаметру заметили еще в эпоху древности. В Двуречье использовали достаточно грубое округление числа до 3 и применяли его при возведении Вавилонской башни. Более точно, как 3,16 π обозначали древнеегипетские математики.
Впервые вычислением «Пи» на научной основе занялся великий античный ученый Архимед (287-212 гг. до н.э), который пришел к мысли о замене длины окружности периметром вписанного в него 96-угольника. В результате получилась архимедово число — дробь 22/7 или 3,14286.
Интересный факт: π вычислено с точностью 31,4 трлн знаков после запятой (на 2019 год).
Открытие Пи
Древние вавилоняне знали о существовании числа Пи уже четыре тысячи лет назад. Вавилонские таблички исчисляют Пи как 3,125, а в египетском математическом папирусе встречается число 3,1605. В Библии число Пи дается в устаревшей длине – в локтях, а греческий математик Архимед использовал для описания Пи теорему Пифагора, геометрическое соотношение длины сторон треугольника и площади фигур внутри и снаружи кругов. Таким образом, можно с уверенностью сказать, что Пи является одним из наиболее древних математических понятий, хоть точное название данного числа и появилось относительно недавно.