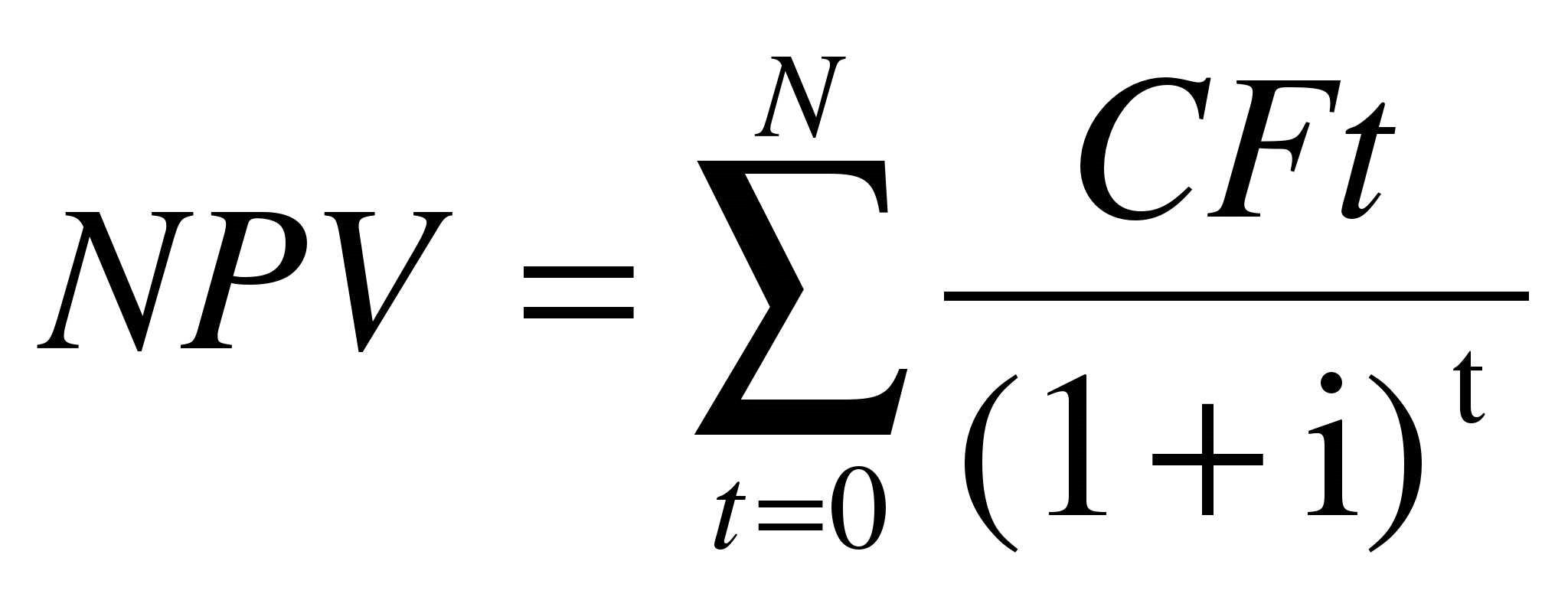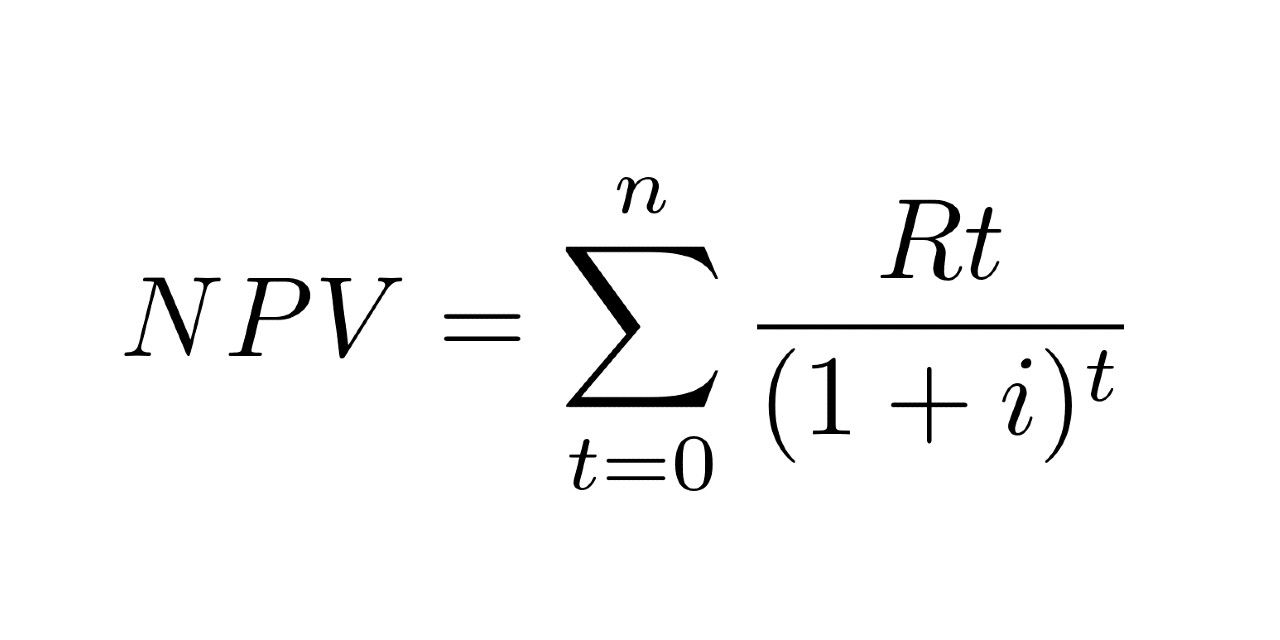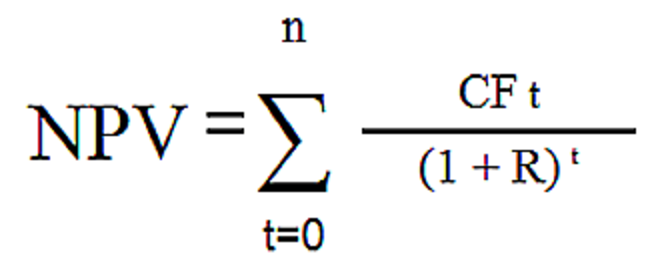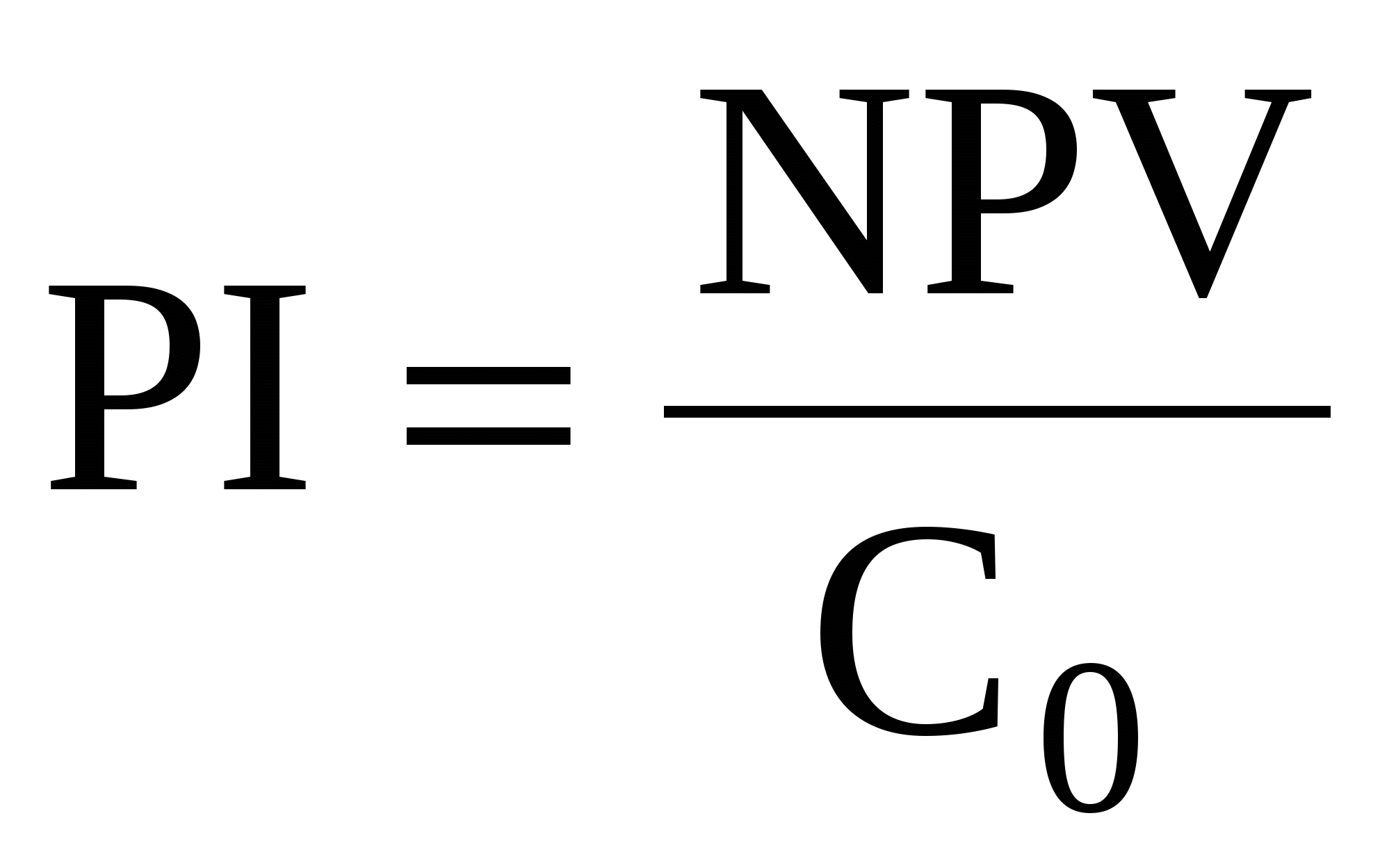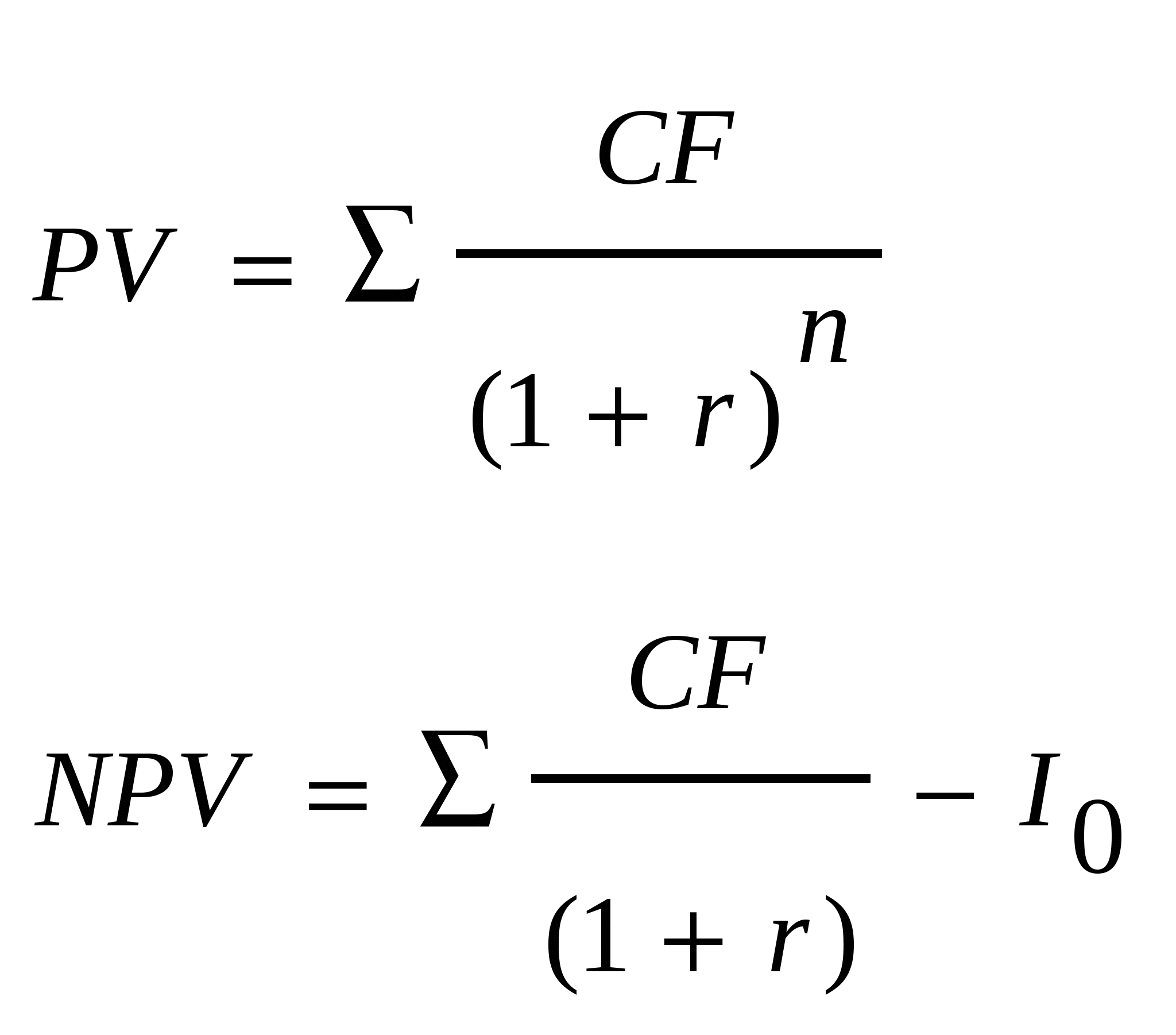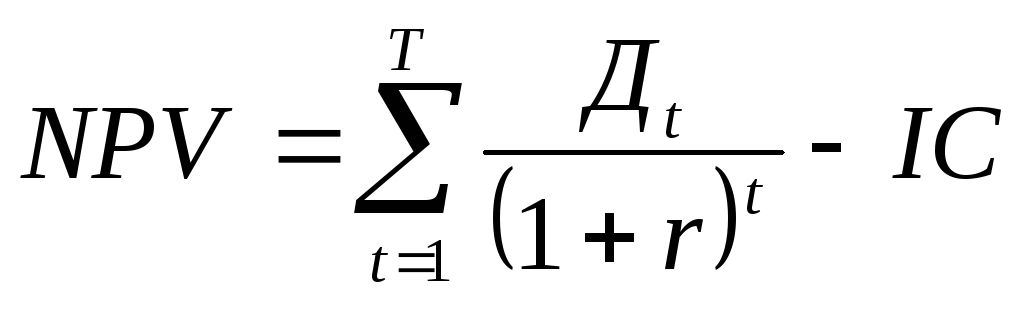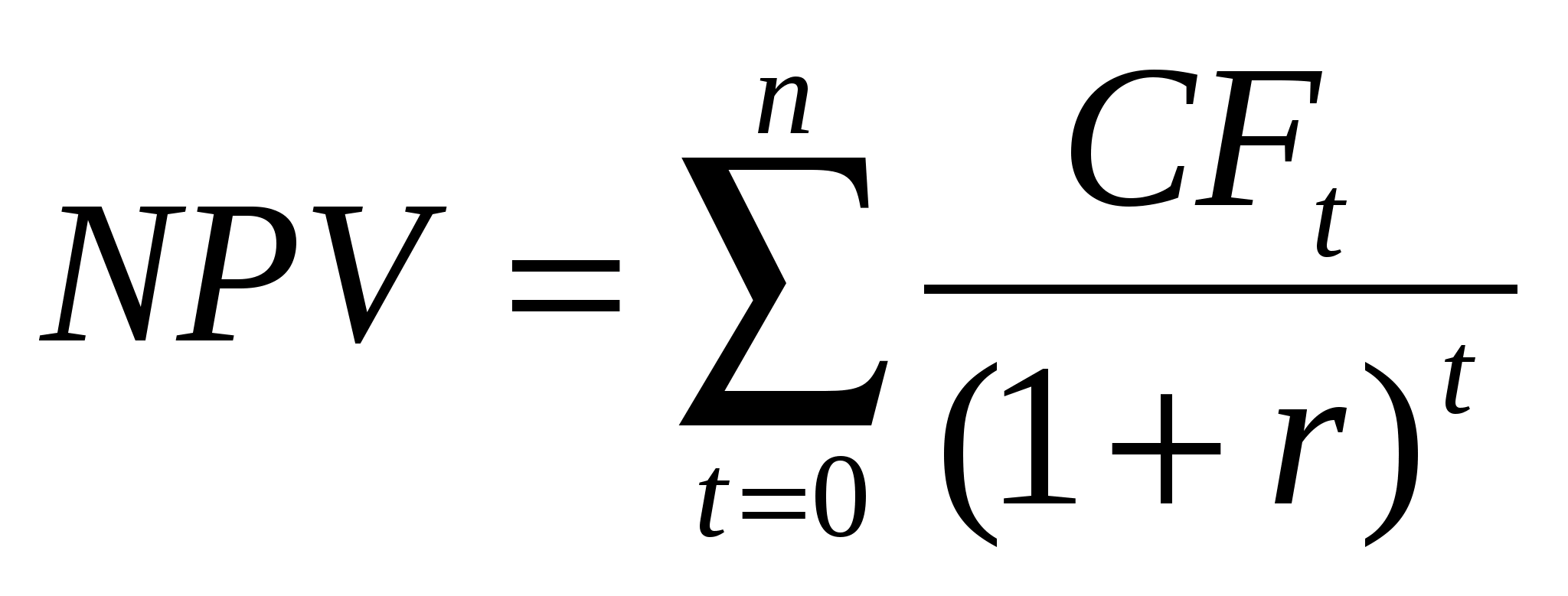Пример расчета NPV
Размер чистой приведенной стоимости инвестиций зависит от размера ставки дисконтирования, чем выше ставка дисконтирования, тем меньше NPV. Выбор ставки дисконтирования основывается на сравнении гипотетической доходности инвестиций в другие проекты или сравнение ее со стоимостью действующего капитала. Такое сравнение дает представление инвестору о барьере минимальной доходности от инвестиций в данном конкретном варианте вложений.

- стоимость действующего капитала в инвестируемом объекте обеспечивает доходность на уровне 16%;
- кредитные ставки банков равны 12 – 14%;
- банковские депозиты обеспечивают доходность 11 -13%;
- уровень доходности финансового рынка с минимальной степенью риска находится на уровне 15%.
Очевидно, что ставка дисконтирования должна быть несколько выше максимальной доходности всех возможных вариантов вложений средств, то есть выше или минимум равна 16%. При равной базовой ставке действующего капитала и норме дисконтирования речь может идти об инвестировании в расширение производства на существующей технологической и технической базе производства.
Вышеприведенная формула расчета NPV исходила из предположения, что инвестиции делаются одномоментно, в начале реализации проекта. В жизни часто такие вложения делаются в течение нескольких лет. В этом случае формула расчета приобретает следующий вид:

где:
- ICt – инвестиции в t-ом году;
- T – период вложений инвестиций.
В данной формуле инвестиционные потоки также приводятся по принятой ставке дисконтирования.
В инвестиционной практике довольно часто встречаются случаи, когда полученная прибыль реинвестируется на определенный период. Чаще всего такая ситуация возникает при недостатке финансирования проекта.
Тогда формула расчета изменяется следующим образом:
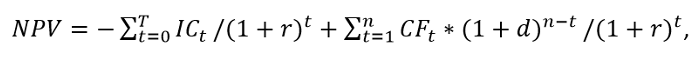
где:
d – процентная ставка реинвестирования капитала.
Для сравнительного анализа инвестиционных проектов соизмеряют их показатели NPV. Инвестиции с большим NPV, признаются предпочтительными.
Достоинством данного показателя является возможность определения чистой накопленной стоимости за весь жизненный цикл инвестиционного проекта, что позволяет сравнивать варианты инвестиций при различных жизненных циклах. Однако на основании этого показателя не всегда возможно ответить на вопрос, какой из вариантов более эффективен по доходности.

- 1 проект за 3 года (жизненный цикл) получит NPV в размере 200 млн. рублей.
- 2 проект в течение 5 лет (жизненный цикл) — 300 млн. рублей.
Их можно в данном случае сравнить по среднегодовому NPV:
- 1 вариант — 66,67 млн. рублей;
- 2 вариант — 60 млн. рублей.
1 вариант предпочтительнее, несмотря на больший размер NPV во 2 варианте. Поэтому, для более точной оценки прибегают к использованию среднегодовой нормы доходности инвестиций IRR, или сравниваемые варианты должны иметь одинаковый жизненный цикл, тогда вариант с большим NPV будет предпочтительнее.
Расчеты данного показателя, особенно для крупных инвестиций, сложны не только технически, но и методически. Первый недостаток легко преодолевается современными вычислительными устройствами, а второй может сказаться на точности проведенных расчетов и привести к неверным оценкам проекта. Поэтому с расчетом данного показателя всегда рассчитываются показатели дисконтированного срока окупаемости вложений DPP и внутренняя норма доходности IRR. Вкупе они дают высокую точность расчетов экономической эффективности любого инвестиционного проекта.
Дисконтированный индекс доходности
Далеко не всегда инвестиции нужны только в самом начале. Чаще же бывает так, что сумма распределена во времени. Например, первые пару лет проект не приносит вообще никакой прибыли, а требует только вложений. Или, например, проект подразумевает несколько этапов с расширением масштаба производства (что-то вроде «вложили — немного прибыли — нужно вложить для расширения — основная прибыль»).
В таких случаях, используют дисконтированный индекс доходности (по сути, модификация индекса для учета дисконтирования инвестиций).
Формула выглядит следующим образом:
где DPI — это дисконтированный индекс доходности,
ICt — это инвестиции за период t,
CFi — это денежный поток за период i,
d — это ставка дисконтирования,
СУММА — это стандартная функция суммирования всех элементов,
t — периоды от 0 до n (количество прогнозируемых периодов),
i — периоды от 1 до n (количество прогнозируемых периодов).
Обратите внимание, что в верхней части формулы отсчет периодов начинается с 1, а в нижней части с 0. Это происходит потому, что учитывают денежные потоки после первоначального периода инвестирования, вложения же могут требоваться в каждый период времени
Немного о сложностях, связанных с чистым дисконтированным доходом
Проблема заключается в том, что нередко значения бывают неточными. Прежде всего, тяжело определиться с величиной двух пунктов, входящих в эту формулу:
- Денежные потоки. Этот пункт включает в себя как изначальную инвестицию, так и деньги, которые поступают в дальнейшем. Если использовать упрощенный пример с депозитом, то денежный поток – это сумма, которая поступает на депозитный счет вклада с капитализацией (то есть, начислением процентов на проценты), а также с пополнением раз в определенный период.
- Ставка дисконтирования. Есть несколько методов, которые позволяют вычислить этот параметр.
Ситуация следующая: достаточно трудно вычислить общую сумму денег, потому что не всегда ясно, насколько увеличатся инвестиции за определенный период.
Вернемся к примеру с депозитом. Мы можем положить деньги и даже запланировать класть, предположим, 5 тысяч долларов каждый месяц. Но может случиться непредвиденная ситуация, и эту сумму пришлось отдать. В результате, месяц пропущен, и эта непредсказуемость сделала совершенные ранее расчеты неверными.
В случае со ставкой дисконтирования сложность связана прежде всего с несколькими моделями. Непонятно, какая из них больше подходит, потому что каждая имеет свои преимущества и недостатки. Давайте детальнее разберем каждый из этих пунктов.
Денежные потоки
Чтобы вычислить величину денежных потоков необходимо от притока денег отнять отток. Например, вы положили на депозит 1000 долларов, но пришлось 200 с него снять, потому что надо купить новый телефон.
Таким образом, денежный поток составляет 800 долларов. Но это все легко в текущем моменте. А чтобы спрогнозировать денежный поток, нужно учесть факторы, формирующие поступления денег и понять связь между ними и увеличением CF.
А этих факторов может быть очень много: экономическая ситуация, подвижность спроса, действия конкурентов, эффективность рекламы и много чего еще. Дополнительные факторы могут быть связаны с конкретным товаром, в производство которого вкладываются деньги. Нужно прогнозировать даже то, сколько товара будет продаваться при заранее установленных ценах
Кроме того, нужно подумать, какие предвиденные и непредвиденные расходы могут быть. Первые – это аренда, цены на сырье, из которого производится товар, зарплаты, налоги и так далее. Это те необходимые траты, о которых вы уже знаете. А вот непредвиденные расходы могут быть разные: обвалился потолок в офисе, и его нужно ремонтировать, клиент подал в суд, и приходится платить издержки и так далее.
А еще надо закладывать возможность, что какая-то продукция окажется некачественной, и придется отзывать товар. Все это может повлиять на реальную, а не прогнозируемую величину денежного потока.
Ставка дисконтирования
Итак, есть четыре модели, которые позволяют рассчитать ставку дисконтирования:
CAPM. Эта модель позволяет понять, как влияют риски на величину ставки. В качестве информационной базы используется биржа ММВБ, исходя из которой определяются размеры акций.
WACC. Эта модель позволяет учесть эффективность и собственного капитала, и денег, взятых в долг
То есть, она принимает во внимание процентные ставки по кредиту.
Модель Росса. Она позволяет учитывать факторы, связанные с рынком.
Модель Гордона
С ее помощью инвестор может понять, сколько составляет дивидендная доходность, исходя из котировок акций.
Как производится расчет?
Прежде чем переходить к подробному изучению формул, необходимо ознакомиться с принципами NPV расчета, а также порядком его проведения.
- Сначала нужно найти разницу между инвестициями и планируемым доходом. При этом нужно брать не весь инвестиционный курс, а отдельно каждый из периодов. Обычно одной такой единицей выступает год.
- На втором этапе определяется дисконтная ставка. Чтобы ее найти, нужно определить стоимость капитала.
- Затем все денежные потоки должны быть переведены на сегодняшнее состояние.
- Находится сумма дисконтных потоков. Это самый интересный пункт, так как именно в нем инвестор узнает объем своих доходов от проекта.
- Принцип расчета по NPV известен. Это значит, что теперь можно знакомиться с формулой, по которой этот расчет производится.
Формула NPV
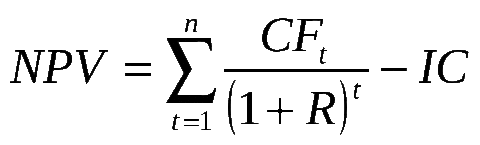
Выглядит сложно и непонятно. Однако если знать значение каждого из элементов, то с подсчетом не должно возникнуть труда.
- N, t – этими буквами обозначаются все временные промежутки, которые встречаются в формуле.
- CFT – потоки денег за время T
- IC – инвестиции, т.е. деньги, вложенные в проект
- R – процентная ставка дисконтов.
После того, как расчет произведен, и величина NPV найдена можно приступать к её анализу.
Формула расчёта NPV
Для расчёта NPV необходимо:
- Составить прогнозный график денежных потоков по инвестиционному проекту в разрезе периодов. Денежные потоки должны включать как доходы (притоки средств), так и расходы (осуществляемые инвестиции и прочие затраты по реализации проекта).
- Определить размер ставки дисконтирования. По сути, ставка дисконтирования отражает предельную норму стоимости капитала инвестора. Например, если для инвестирования будут использованы заёмные средства банка, то ставкой дисконтирования будет являться эффективная ставка процента по кредиту. Если же будут использованы собственные средства инвестора, то за ставку дисконтирования может быть взята ставка процента по банковскому депозиту, ставка доходности по государственным облигациям и т.п.
Расчёт NPV осуществляется по следующей формуле:
гдеNPV (Net Present Value) — чистая текущая стоимость инвестиционного проекта;CF (Cash Flow) — денежный поток;r — ставка дисконтирования;n — общее количество периодов (интервалов, шагов) i = 0, 1, 2, …, n за весь срок инвестирования.
В данной формуле CF соответствует объёму первоначальных инвестиций IC (Invested Capital), т.е. CF= IC. При этом денежный поток CF имеет отрицательное значение.
Поэтому, вышеуказанную формулу можно модифицировать:
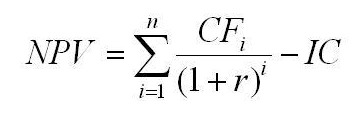
Если инвестиции в проект осуществляются не одномоментно, а на протяжении ряда периодов, то инвестиционные вложения также должны быть продисконтированны. В таком случае формула NPV проекта примет следующий вид:

Пример расчета по NPV
Чтобы лучше понять, как это работает, разберем примеры.
Инвестору предлагают два равно неизвестных варианта вложения денег. Условно обозначим эти проекты А и Б. При этом проект А обеспечивает резкий возврат средств, угасающий со временем. А проект Б увеличивает выгоды постепенно. Дисконт в обоих случаях составляет десять процентов. Схематически это выглядит примерно так:
А
| Год | Денежные средства |
| -20000 | |
| 1 | 10000 |
| 2 | 4000 |
| 3 | 3000 |
Б
| Год | Деньги |
| -10000 | |
| 1 | 1000 |
| 2 | 3000 |
| 3 | 5000 |
Рентабельность можно найти либо рассчитав все вручную, либо воспользовавшись программой Excel. В разделе экономических формул присутствует необходимая нам формула ЧПС.

После всех вычислений получаем:
- Для А получаем, что значение отрицательно и равно минус 2400 рублей (-2400 руб.).
- Для Б – минус семьсот двадцать семь (-727 руб.).
Таким образом, для инвестиций оказался непригоден ни один из проектов. При том, что потери в проекте А больше.
NPV: формула расчета (пример)
Задача. Имеется три потенциальных проекта для инвестиций. Первоначальные инвестиции С в каждый из них составляют 400 условных единиц. Известна прибыль (Пn) , которую смогут генерировать проекты в ближайшие пять лет:
| Проект | Начальные инвестиции |
Прибыль по годам | ||||
| П1 | П2 | П3 | П4 | П5 | ||
| Проект 1 | 400 | 80 | 105 | 120 | 135 | 150 |
| Проект 2 | 400 | 100 | 117 | 124 | 131 | 118 |
| Проект 3 | 400 | 100 | 125 | 90 | 130 | 145 |
Норма прибыли i составляет 13 %. Необходимо выбрать наиболее выгодный проект, используя формулу NPV.
Решение. Интересующая нас формула имеет следующий вид:
В этой формуле CFt обозначает чистый эффективный денежный поток на t-ом годичном интервале, i — ставка дисконтирования (в десятичном выражении), N – количество лет.
В представленной формуле главное разглядеть фактор (коэффициент) дисконтирования 1/(1 + i)t.
В нашем случае для t = 0 он будет равен 1, для t = 1: 1/(1+0,13)1 = 0,885 и т.д.
Рассчитаем значения NPV для каждого из трех проектов, используя табличное представление (оно более наглядно).
| Проект 1 | |||
| Год | Денежный поток |
Коэффициент дисконтирования |
Дисконтированный денежный поток |
| -400 | 1,000 | -400 | |
| 1 | 80 | 0,885 | 70,80 |
| 2 | 105 | 0,783 | 82,22 |
| 3 | 120 | 0,693 | 83,16 |
| 4 | 135 | 0,613 | 82,76 |
| 5 | 150 | 0,543 | 81,45 |
| NPV = | 0,39 |
| Проект 2 | |||
| Год | Денежный поток |
Коэффициент дисконтирования |
Дисконтированный денежный поток |
| -400 | 1,000 | -400 | |
| 1 | 100 | 0,885 | 88,50 |
| 2 | 117 | 0,783 | 91,61 |
| 3 | 124 | 0,693 | 85,93 |
| 4 | 131 | 0,613 | 80,30 |
| 5 | 118 | 0,543 | 64,07 |
| NPV = | 10,41 |
| Проект 3 | |||
| Год | Денежный поток |
Коэффициент дисконтирования |
Дисконтированный денежный поток |
| -400 | 1,000 | -400 | |
| 1 | 100 | 0,885 | 88,50 |
| 2 | 125 | 0,783 | 97,88 |
| 3 | 90 | 0,693 | 62,37 |
| 4 | 130 | 0,613 | 79,69 |
| 5 | 145 | 0,543 | 78,74 |
| NPV = | 7,18 |
Наибольший NPV имеет проект 2. С точки зрения NPV, этот проект и является самым выгодным.
Разумеется, вместо таблиц мы бы могли использовать иное представление решения:
NPV1 = -400 * 1,000 + 80 * 0,885 + 105 * 0,783 + 120 * 0,693 + 135 * 0,613 + 150 * 0,543 = 0,39
NPV2 = -400 * 1,000 + 100 * 0,885 + 117 * 0,783 + 124 * 0,693 + 131 * 0,613 + 118 * 0,543 = 10,41
NPV3 = -400 * 1,000 + 100 * 0,885 + 125 * 0,783 + 90 * 0,693 + 130 * 0,613 + 145 * 0,543 = 7,18
Результат расчета NPV будет тот же.
На этом простом примере мы показали, как считать NPV, когда заранее известен объем первоначальных инвестиций и ожидаемые размеры прибыли на ближайшую перспективу.
На практике эти значения известны далеко не всегда, что существенно усложняет задачу выбора наиболее выгодного инвестиционного проекта.
Применение одного лишь метода NPV в таких ситуация может привести к неверным выводам: либо прибыль окажется невысока, либо ждать ее придется неоправданно долго.
Компенсировать недостатки NPV призваны другие расчетные показатели (уже упомянутый нами IRR, отражающий внутреннюю норму доходности, и некоторые другие).
Думается, после проработки сегодняшней статьи вы уже не будете задаваться вопросом при виде загадочной трехбуквицы NPV, что это такое и как рассчитать сей показатель.
Удачных инвестиций!
Что такое чистая приведенная стоимость и правило чистой приведенной стоимости?
Чистая приведенная стоимость характеризует стоимость инвестиций, а правило чистой приведенной стоимости — это метод выбора среди альтернативных инвестиций.
Чистая приведенная стоимость инвестиций (NPV, от англ. ‘net present value’) — это приведенная (текущая) стоимость притока денежных средств за вычетом приведенной стоимости оттока денежных средств.
Слово «чистая» (англ. ‘net’) в этом термине означает вычитание приведенной стоимости оттоков (затрат) инвестиций из приведенной стоимости притоков (доходов) для получения чистого финансового результата.
Процедура вычисления NPV и применения правила NPV заключаются в следующем:
1. Определите все денежные потоки, связанные с инвестициями — все притоки и оттоки.
При оценке денежных потоков мы руководствуемся двумя принципами.
- Во-первых, мы включаем в расчет только дополнительные денежные потоки, возникающие в результате осуществления проекта. Мы не учитывает невозвратные затраты (англ. ‘sunk costs’), т.е. расходы, которые были совершены до начала проекта и которые нельзя возместить в течение проекта.
- Во-вторых, мы учитываем налоговые последствия, используя стоимость денежных потоков после уплаты налогов.
Для дисконтирования денежных потоков часто используется средневзвешенная стоимость капитала (WACC).
Этот показатель представляет собой средневзвешенное значение ставок доходности после налогообложения для обыкновенных акций, привилегированных акций и долгосрочных долговых обязательств компании, где весом является доля каждого источника финансирования в целевой структуре капитала компании.
4. Суммируйте все приведенные значения стоимости.
Сумма приведенной стоимости всех денежных потоков (притоков и оттоков) является чистой приведенной стоимостью инвестиций.
5. Примените правило чистой приведенной стоимости.
Правило NPV (англ. ‘net present value rule’) заключается в следующем:
- Если NPV инвестиции является положительным значением, инвестор должен ее осуществить.
- Если NPV отрицательна, инвестор не должен осуществлять эту инвестицию.
- Если у инвестора есть две возможные инвестиции, но он может выбрать только одну (т.е. взаимоисключающие проекты), инвестору следует выбрать инвестицию с более высокой положительной NPV.
Краткое описание приведённой стоимости
Когда человек вкладывает свои деньги в стоимость бизнес-проекта, то он обязательно должен изучить целесообразность указанных манипуляций, с экономической точки зрения. Ведь пользователь заинтересован не только в полном объёме окупить все потраченные средства, но и получить допналичные сверх исходных взносов. Помимо этого, специалист должен отыскать альтернативные методы инвестирования, при таком же риске приносящие лучший уровень дохода. Чтобы не потерять свой капитал, нужно заранее определить чистую стоимость идеи (приведённую NPV). Этот подход имеет множество преимуществ.
Чистая приведённая стоимость представляет для проекта универсальный показатель КПД. Все расчёты проводятся путём дисконтирования предполагаемых финпотоков (расходов и доходов). На прибыль указывает приведённая стоимостная чистая оценка плана-проекта. Когда финпотоки в полном объёме окупят все стартовые инвестиционные затраты и периодические финансовые оттоки, можно будет прибросить точные данные.
https://youtube.com/watch?v=bsnE3jk6IDE
Само вычисление показателя приведённой стоимости должно проводиться поэтапно:
- Эксперт должен найти различия между прогнозной прибылью и инвестзатратами за каждый временной промежуток (чаще всего за год).
- Определяется дисконт-ставка. Чтобы не ошибиться в расчётах, нужно реально оценить стоимость имеющегося капитала.
- Все полученные результаты необходимо привести к моменту сегодняшнего дня (эксперт должен посчитать дисконт для каждого финпотока отдельно за каждый временной период).
- На финальном этапе нужно сложить вместе все поступающие и отчисляемые финсредства. Итоговое значение выразит приведённую стоимость, отображающую общую прибыль для вкладчика.
Как рассчитать приведенную стоимость
Очевидно, 330 тыс.долл., которые мы получим в будущем, стоят дешевле 330 тыс. долл., которыми мы располагаем сегодня. И дело не только в инфляции.
Основная причина такого положения вещей в том, что мы можем имеющиеся 330 тыс. долл. инвестировать в безрисковые финансовые инструменты наподобие банковских депозитов или государственных облигаций.
В таком случае для определения «истинной» стоимости наших 330 тыс. долл. к ним требуется присовокупить еще и процентный доход по соответствующему депозиту (ценной бумаге).
На эту ситуацию можно посмотреть так: сегодняшние 330 тыс. долл. будут стоит в будущем столько же плюс – процентный доход по безрисковым финансовым инструментам.
Мы вплотную приблизились к пониманию одного из важнейших принципов теории инвестирования: деньги СЕГОДНЯ стоят ДОРОЖЕ, чем деньги, которые мы получим ЗАВТРА.
Именно поэтому приведенная стоимость любого дохода в будущем будет МЕНЬШЕ его номинального значения, и чтобы его найти, нужно ожидаемый доход умножить на некоторый коэффициент, заведомо МЕНЬШИЙ единицы.
Обычно этот коэффициент именуется коэффициентом дисконтирования.
Математическая запись нашего постулата будет иметь следующий вид:
PV = DF * C1, где
PV – приведенная стоимость (от англ. present value),
DF – коэффициент (или – фактор) дисконтирования (от англ. discount factor),
C1 – ожидаемый через 1 год доход.
Сущность коэффициента дисконтирования может быть истолкована так: это нынешняя стоимость 1 доллара, который мы рассчитываем получить в будущем. Численно он будет равен следующему отношению:
DF = 1 / (1 + r), где
r – размер вознаграждения (норма доходности), на который вправе рассчитывать инвестор в связи с отсрочкой получения дохода.
Итак, мы готовы к тому, чтобы рассчитать, наконец, приведенную стоимость будущих доходов от наших инвестиций.
Для этого введем в условия задачи размер процентной ставки по безрисковым финансовым инструментам, равный, к примеру, 8 процентам годовых.
В таком случае ставка дисконтирования будет равняться значению дроби 1 / (1 + 0,08):
DF = 1 / (1 + 0,08) = 1 / 1,08 = 0,926.
Приведенную стоимость 330 тыс. долл. мы рассчитаем так:
PV = DF * C1 = 0,926 * 330 000 долл. = 305 580 долл.
Сложности расчетов
По формуле рассчитать NPV нетрудно, достаточно навыков, полученных на уроках математики. Задачка для шестиклассника. Вася Петров дал Пете Курочкину 100 рублей год назад и 20 рублей вчера. Сколько денег получит Вася через три года, если Петя обещал вернуть на 24 % больше полученной суммы?
Рассчитанный результат должен учитывать реальную стоимость денег на текущий момент, а она зависит не только от инфляции. Верный NPV, то есть тот, что даст нам самую точную оценку, зависит от правильности определения величины ставки дисконтирования. Вот в чем сложность!
А Васю Петрова на самом деле интересует, хватит ли ему на велосипед, который год назад стоил 117 рублей, а сейчас 126. Денежные потоки и куда они текутДенежными потоками называют движение финансов. Запомнить просто:
- отдаем деньги — отрицательный поток
- получаем — положительный.
Определение ставки дисконтирования R
% ставку, задействованную в переоценке предполагаемых инвестиционных поступлений в общий показатель текущей стоимости, называют дисконтставкой. Обычно это % отчисление, под которое инвестор имеет возможность привлекать денежные финсредства в проект.
Существует несколько способов привлечения инвестиционных финресурсов:
- оформление банковского кредита;
- получение инвестиционного займа на выгодных условиях;
- внесение личных накоплений, полученных от продажи имущества или вывода капитала из других проектов.
Стоимость средств компании будет отличаться в любом из перечисленных вариантов. Даже кредитные ставки существенно различаются исходя из платёжеспособности компании, продолжительности, суммарного объёма инвестиционных средств и наличия залога.