Виды углов между прямыми, основные примеры

См. также

Углы Эйлера
Двугранный угол
Трёхгранный угол
Телесный угол
Азимут (геодезия)
Магнитный азимут
Азимут (астрономия)
Угловой размер
Угол места
Угол скольжения
Румб
Кастор (угол)
Золотое сечение
Угол обзора
Угол поля зрения объектива
Угловое разрешение
Угол поворота
Угол (наклона, уклона)
Угловая скорость (& CAV)
Угловое ускорение
Угловая частота
Угловой коэффициент (Линейная функция)
Изогона
Закон постоянства углов
Решение треугольников
Ортогональность
Тригонометрия
Пентагон (значения)
Полигонометрия
Триангуляция
Позиционный угол и Угловое расстояние (Полярные координаты)
Аспект (астрология)
Склонение (астрономия) и Часовой угол (Системы небесных координат)
Дирекционный угол
Тригонометрический параллакс & Параллактический угол
Астрономическая рефракция

Элементы тупоугольного треугольника:

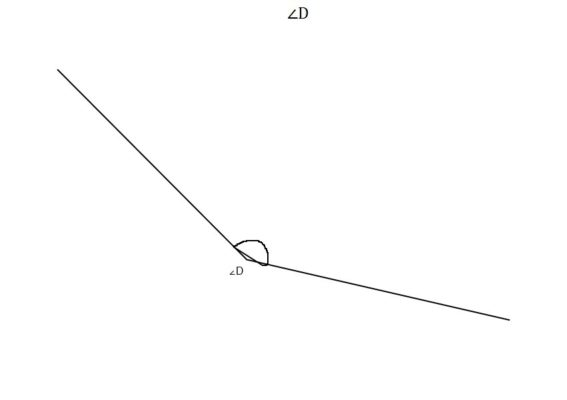
Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

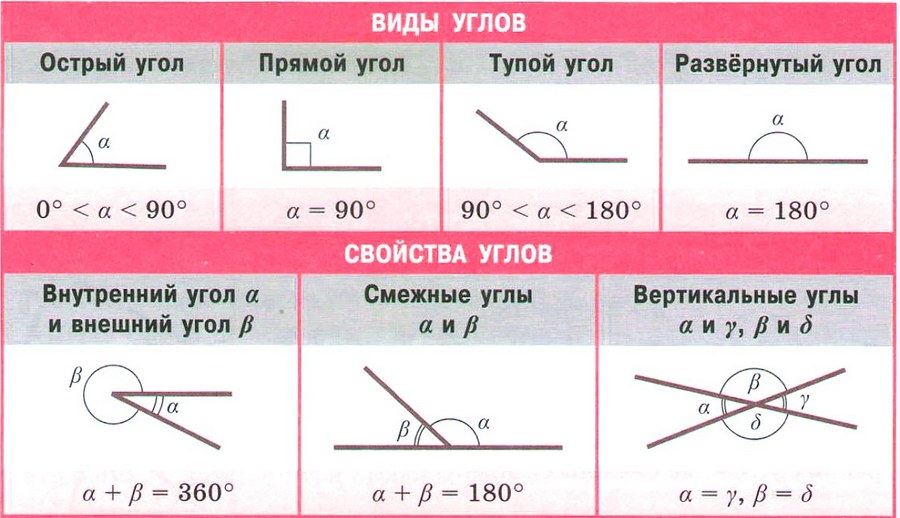
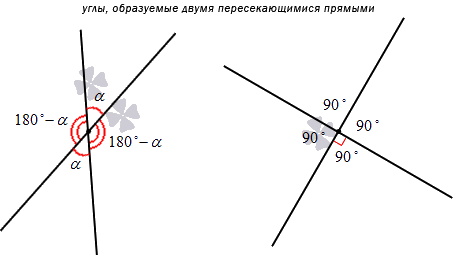
Типы углов

В зависимости от величины углы называются следующим образом.

Нулевой угол (0°); стороны нулевого угла совпадают, его внутренняя область — пустое множество.
Острый угол (от 0° до 90°, не включая граничные значения).
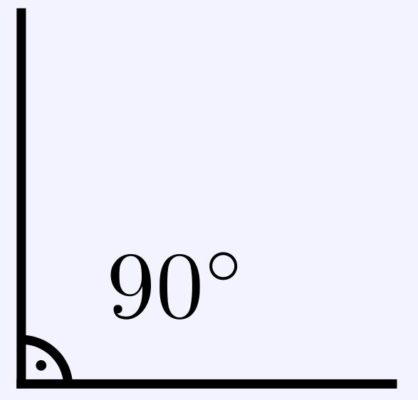
Прямой угол (90°); стороны прямого угла перпендикулярны друг другу.
Тупой угол (от 90° до 180°, не включая граничные значения).
Косой угол (любой, не равный 0°, 90°, 180° или 270°).
Развёрнутый угол (180°); сторонами развёрнутого угла являются две полупрямые одной прямой, то есть два луча, направленных в противоположные стороны.
Выпуклый угол (от 0° до 180° включительно)[источник не указан 186 дней].
Невыпуклый угол (от 180° до 360°, не включая граничные значения)[источник не указан 186 дней].
Полный угол (360°) — см. оборот (единица измерения).

См. также: Центральный угол

Вариации и обобщения

Величиной ориентированного угла между прямыми AB{\displaystyle AB}и CD{\displaystyle CD} (обозначение: ∠(AB,CD){\displaystyle \angle (AB,CD)}) называют величину угла, на который нужно повернуть против часовой стрелки прямую AB{\displaystyle AB} так, чтобы она стала параллельна прямой CD.{\displaystyle CD.} При этом углы, отличающиеся на n·180° (n — целое число), считаются равными. Следует отметить, что ориентированный угол между прямыми CD{\displaystyle CD} и AB{\displaystyle AB} не равен ориентированному углу между прямыми AB{\displaystyle AB} и CD{\displaystyle CD} (они составляют в сумме 180° или, что по нашему соглашению то же самое, 0°). Ориентированные углы обладают следующими свойствами: а) ∠(AB,BC)=−∠(BC,AB);{\displaystyle \angle (AB,BC)=-\angle (BC,AB);} б) ∠(AB,CD)+∠(CD,EF)=∠(AB,EF);{\displaystyle \angle (AB,CD)+\angle (CD,EF)=\angle (AB,EF);} в) точки A,B,C,D,{\displaystyle A,B,C,D,} не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда ∠(AB,BC)=∠(AD,DC).{\displaystyle \angle (AB,BC)=\angle (AD,DC).}

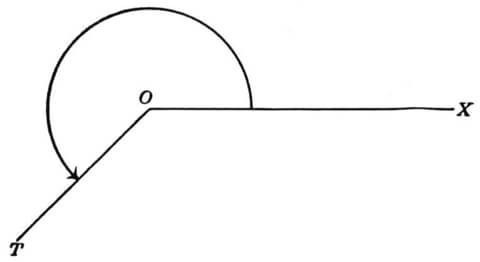
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла, расширив его область определения на всю числовую прямую (−∞;+∞){\displaystyle (-\infty ;+\infty )}: вводятся углы, большие 360°, в зависимости от направления вращения различают положительные и отрицательные углы. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Понятие угла обобщается на рассматриваемый в стереометрии телесный угол.

Телесный угол

Основная статья: Телесный угол

Обобщением плоского угла на стереометрию является телесный угол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол).

Телесные углы измеряются в стерадианах (одна из основных единиц СИ), а также во внесистемных единицах — в частях полной сферы (то есть полного телесного угла, составляющего 4π стерадиан), в квадратных градусах, квадратных минутах и квадратных секундах.

Телесными углами являются, в частности, следующие геометрические тела:

двугранный угол — часть пространства, ограниченная двумя пересекающимися плоскостями;
трёхгранный угол — часть пространства, ограниченная тремя пересекающимися плоскостями;
многогранный угол — часть пространства, ограниченная несколькими плоскостями, пересекающимися в одной точке.

Двугранный угол может характеризоваться как линейным углом (углом между образующими его плоскостями), так и телесным углом (в качестве вершины может быть выбрана любая точка на его ребре — прямой пересечения его граней). Если линейный угол двугранного угла (в радианах) равен φ, то его телесный угол (в стерадианах) равен 2φ.

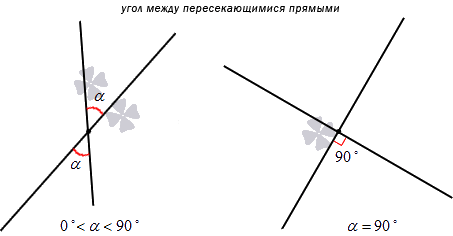
Угол между кривыми

Угол между двумя кривыми в точке Р определяется как угол между касательными А и В в P.

Как в планиметрии, так и в стереометрии, а также в ряде других геометрий можно определить угол между гладкими кривыми в точке пересечения: по определению, его величина равна величине угла между касательными к кривым в точке пересечения.

Замечательные линии тупоугольного треугольника

Во всех треугольниках, имеющих тупые углы, есть линии, называемые замечательными. Первая из них – высота. Она представляет собой перпендикуляр из одной из вершин на соответствующую ей сторону. Все высоты сталкиваются в точке, которая именуется как ортоцентр. В треугольнике с тупыми углами он будет находиться за пределами самой фигуры. Что касается острых углов, то центр там находится в самом треугольнике.

Еще одна линия – медиана. Это черта, проведенная от вершины к центру соответствующей стороны. Все медианы сходятся в треугольнике, а место их совмещения – это центр тяжести такого многоугольника.

Биссектриса – линия, делящая пополам как тупые углы, так и остальные. Пересечение трех таких линий всегда бывает только в самой фигуре и определяется как центр круга, вписанного в треугольник.

В свою очередь, центр круга, описанного вокруг фигуры, можно получить из трех срединных перпендикуляров. Это линии, которые были опущены из середин прямых, соединяющих вершины. Место пересечения трех срединных перпендикуляров в треугольнике, имеющем тупые углы, находится снаружи фигуры.

Угол и скалярное произведение

Понятие угла можно определить для линейных пространств произвольной природы (и произвольной, в том числе бесконечной размерности), на которых аксиоматически введено положительно определённое скалярное произведение (x,y){\displaystyle (x,y)} между двумя элементами пространства x{\displaystyle x} и y.{\displaystyle y.} Скалярное произведение позволяет определить также и так называемую норму (длину) элемента как квадратный корень произведения элемента на себя ||x||=(x,x).{\displaystyle ||x||={\sqrt {(x,x)}}.} Из аксиом скалярного произведения следует неравенство Коши — Буняковского (Коши — Шварца) для скалярного произведения: |(x,y)|⩽||x||⋅||y||,{\displaystyle |(x,y)|\leqslant ||x||\cdot ||y||,} откуда следует, что величина (x,y)||x||⋅||y||{\displaystyle {\frac {(x,y)}{||x||\cdot ||y||}}} принимает значения от −1 до 1, причём крайние значения достигаются тогда и только тогда, когда элементы пропорциональны (коллинеарны) друг другу (говоря геометрически — их направления совпадают или противоположны). Это позволяет интерпретировать отношение (x,y)||x||⋅||y||{\displaystyle {\frac {(x,y)}{||x||\cdot ||y||}}} как косинус угла между элементами x{\displaystyle x} и y.{\displaystyle y.} В частности, элементы называют ортогональными, если скалярное произведение (или косинус угла) равно нулю.

В частности, можно ввести понятие угла между непрерывными на некотором интервале a,b{\displaystyle } функциями, если ввести стандартное скалярное произведение (f,g)=∫abf(x)g(x)dx,{\displaystyle (f,g)=\int _{a}^{b}f(x)g(x)dx,} тогда нормы функций определяются как ||f||2=∫abf2(x)dx.{\displaystyle ||f||^{2}=\int _{a}^{b}f^{2}(x)dx.} Тогда косинус угла определяется стандартным образом как отношение скалярного произведения функций к их нормам. Функции также можно назвать ортогональными, если их скалярное произведение (интеграл их произведения) равно нулю.

В римановой геометрии можно аналогично определить угол между касательными векторами с помощью метрического тензора gij.{\displaystyle g_{ij}.} Скалярное произведение касательных векторов u{\displaystyle u} и v{\displaystyle v} в тензорной записи будет иметь вид: (u,v)=gijuivj,{\displaystyle (u,v)=g_{ij}u^{i}v^{j},} соответственно нормы векторов — ||u||=|gijuiuj|{\displaystyle ||u||={\sqrt {|g_{ij}u^{i}u^{j}|}}} и ||v||=|gijvivj|.{\displaystyle ||v||={\sqrt {|g_{ij}v^{i}v^{j}|}}.} Поэтому косинус угла будет определяться по стандартной формуле отношения указанного скалярного произведения к нормам векторов: cos⁡θ=(u,v)||u||⋅||v||=gijuivj|gijuiuj|⋅|gijvivj|.{\displaystyle \cos \theta ={\frac {(u,v)}{||u||\cdot ||v||}}={\frac {g_{ij}u^{i}v^{j}}{\sqrt {|g_{ij}u^{i}u^{j}|\cdot |g_{ij}v^{i}v^{j}|}}}.}

Когда изучаются

Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию

В каждом из них немалое внимание уделяется углам:

В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
В стереометрии изучаются пространственные углы – двугранные и трехгранные.

Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии

Что такое угол?

Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят, — вершиной угла. На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.

При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.

Например, вместо «угол АОВ» пишут короче: «угол О».

Вместо слова «угол» пишут знак .

Например, AОВ, O.

На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.

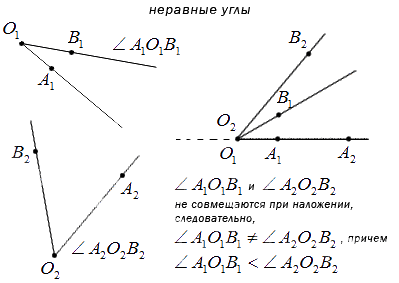
Как и все геометрические фигуры, углы сравниваются с помощью наложения.

Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.

Например, на рисунке 162 ABC = MNK.

Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.

Пишут: COP < COK и POK < COK.

Литература

Барабанов О.О. Начала истории прямого угла // История науки и техники, 2015. №1. С. 16-27.*
Сидоров Л. А. Угол // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1985. — Т. 5. — С. 459‒460. — 623 с. — 150 000 экз.
Двугранный угол // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1979. — Т. 2. — С. 50. — 552 с. — 150 000 экз.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30‒31. — ISBN 5-94057-170-0.
Угломерные приборы/Угол (плоский) // Большая Советская энциклопедия (в 30 т.) / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская Энциклопедия», 1977. — Т. XXVI. — С. 459‒460. — 624 с.
K. Menger. New Fondations of Euclidean Geometry (англ.) // THE AMERICAN JOURNAL OF MATHEMATICS 53 : журнал. — 1931. — P. 721‒745.

Тупоугольный треугольник (понятие и определение):

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов

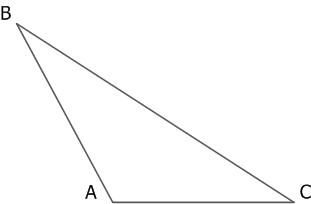
Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

∠ АВС, ∠ BСA – острые углы треугольника

По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник, т.к. у него каждый угол составляет 60°.

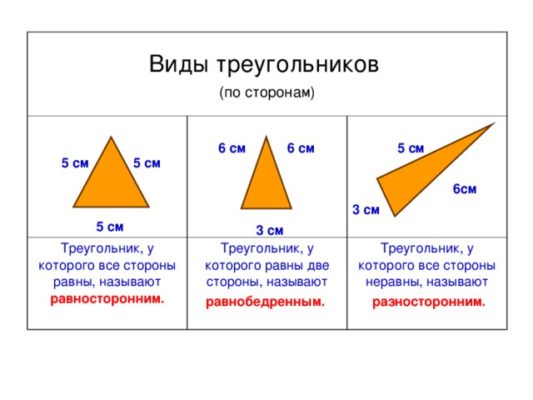
Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.

Рис. 3. Прямоугольный треугольник

Тупоугольный треугольник также может быть одновременно равнобедренным треугольником. Но не всякий равнобедренный треугольник тупой.

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

∠ ВАС – вершинный угол, ∠ АBC и ∠ BСA – углы при основании

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Угол в метрическом пространстве

Также существует ряд работ, в которых вводится понятие угла между элементами метрического пространства.

Пусть (X,ρ){\displaystyle (X,\rho )} — метрическое пространство. Пусть далее, x,y,z{\displaystyle x,y,z} — элементы этого пространства.

К. Менгер ввёл понятие угла между вершинами y{\displaystyle y} и z{\displaystyle z} с вершиной в точке x{\displaystyle x} как неотрицательное число yxz^{\displaystyle {\widehat {yxz}}}, которое удовлетворяет трём аксиомам:

yxz^=zxy^{\displaystyle {\widehat {yxz}}={\widehat {zxy}}}
yxz^={\displaystyle {\widehat {yxz}}=0} тогда и только тогда, когда ρ(y,z)=|ρ(x,y)−ρ(x,z)|{\displaystyle \rho (y,z)=|\rho (x,y)-\rho (x,z)|}
yxz^=π{\displaystyle {\widehat {yxz}}=\pi } тогда и только тогда, когда ρ(y,z)=ρ(x,y)+ρ(x,z){\displaystyle \rho (y,z)=\rho (x,y)+\rho (x,z)}

В 1932 году Вильсон рассмотрел в качестве угла следующее выражение:

yxz^w=arccos⁡ρ2(x,y)+ρ2(x,z)−ρ2(y,z)2ρ(x,y)ρ(x,z){\displaystyle {\widehat {yxz}}_{w}=\arccos {\frac {\rho ^{2}(x,y)+\rho ^{2}(x,z)-\rho ^{2}(y,z)}{2\rho (x,y)\rho (x,z)}}}

Нетрудно видеть, что введённое выражение всегда имеет смысл и удовлетворяет трём аксиомам Менгера.

Кроме того, угол Вильсона обладает тем свойством, что в евклидовом пространстве он эквивалентен углу между элементами y−x{\displaystyle y-x} и z−x{\displaystyle z-x} в смысле евклидова пространства.

Определение и параметры треугольника

Как уже было отмечено, треугольник – это один из видов многоугольников, имеющий три вершины и столько же прямых, их объединяющих. Обозначают линии, как правило, одинаково: углы – маленькими латинскими буквами, а противоположные стороны каждого – соответствующей большой буквой.

Если сложить все углы какого-либо треугольника, получится сумма в 180 градусов. Чтобы узнать внутренний угол, нужно из 180градусов вычесть величину внешнего угла треугольника. Для того чтобы узнать, чему равняется угол, находящийся снаружи, стоит сложить два раздельных от него угла внутри.

В каждом треугольнике, имеет он острые или тупые углы, противоположно большому углу находится наибольшая сторона. Если же прямые между вершинами одинаковы, то, соответственно, и каждый угол равняется 60 градусам.

Обозначение углов

«∠», обозначение угла в геометрии.

Для обозначения угла имеется общепринятый символ: ∠,{\displaystyle \angle ,} предложенный в 1634 году французским математиком Пьером Эригоном.

В математических выражениях углы часто обозначают строчными греческими буквами: α, β, γ, θ, φ и др. Как правило, данные обозначения также наносятся на чертёж для устранения неоднозначности в выборе внутренней области угла. Чтобы избежать путаницы с числом пи, символ π, как правило, для этой цели не используется. Для обозначения телесных углов (см. ниже) часто применяют буквы ω и Ω.

Также часто угол обозначают тремя символами точек, например ∠ABC.{\displaystyle \angle ABC.} В такой записи B{\displaystyle B} — вершина, а A{\displaystyle A} и C{\displaystyle C} — точки, лежащие на разных сторонах угла. В связи с выбором в математике направления отсчёта углов против часовой стрелки, точки, лежащие на сторонах в обозначении угла принято перечислять также против часовой стрелки. Это соглашение позволяет обеспечить однозначность при различении двух плоских углов с общими сторонами, но различными внутренними областями. В тех случаях, когда выбор внутренней области плоского угла ясен из контекста, либо указывается другим способом, данное соглашение может нарушаться.
См. .

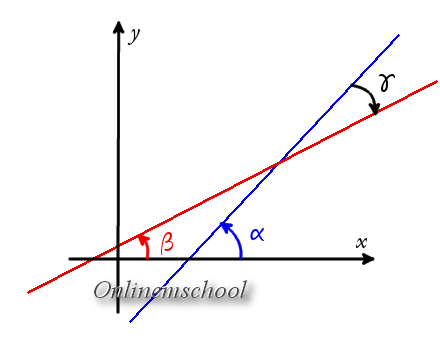
Реже используются обозначения прямых, образующих стороны угла. Например, ∠(bc){\displaystyle \angle (bc)} — здесь предполагается, что имеется в виду внутренний угол треугольника ∠BAC{\displaystyle \angle BAC}, α, который надо было бы обозначить ∠(cb){\displaystyle \angle (cb)}.

Так, для рисунка справа записи γ, ∠ACB{\displaystyle \angle ACB} и ∠(ba){\displaystyle \angle (ba)} означают один и тот же угол.

Иногда для обозначения углов используются строчные латинские буквы (a, b, c, …) и цифры.

На чертежах углы отмечаются небольшими одинарными, двойными или тройными дужками, проходящими по внутренней области угла с центрами в вершине угла. Равенство углов может отмечаться одинаковой кратностью дужек или одинаковым количеством поперечных штрихов на дужке. Если необходимо указать направление отсчёта угла, оно отмечается стрелкой на дужке. Прямые углы отмечаются не дужками, а двумя соединёнными равными отрезками, расположенными таким образом, что вместе со сторонами они образуют небольшой квадрат, одна из вершин которого совпадает с вершиной угла.

Определение и параметры треугольника

Определение

Что такое угол? Существует три определения угла. Рассмотрим каждое из них, выберем наиболее простое и понятное.

Угол – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. То есть это просто два луча. Это определение дается практически в каждом учебнике геометрии. Оно правильное, но прочитав его, не совсем понятно, откуда берется значение угла.

Угол – это плоскость, ограниченная двумя лучами, исходящими из одной точки. То есть, два луча “откусывают кусочек пространства”.

Угол – это мера поворота луча, вокруг своего начала. Это сложно понять, но легко представить. Представьте часы. Вот на часах 12 часов дня, минутная и часовая стрелка находятся на одном уровне, тут минутная стрелка начинает двигаться. И каждый раз, время, а значит положение стрелок можно определить именно углом между часовой и минутной стрелкой. Углы могут быть разными, но если выделять угол в каждый момент времени дугой, то можно заметить, что дуга в конце концов превратится в круг.

Именно круг и является началом отчета для градуса. Дуга $$1\over360$$ части круга это градус. А по количеству градусов в угле можно выделить основные виды углов между прямыми: острые, прямые, тупые и полные углы.

Тупоугольный треугольник

Тупой угол треугольника всегда больше 90-градусного угла, но меньше развернутого. Таким образом, тупой угол равен от 90 до 180 градусов.

Возникает вопрос: бывает ли более одного тупого угла в такой фигуре? Ответ находится на поверхности: нет, потому что сумма углов должна быть менее 180. Если два угла будут иметь, например, по 95 градусов, то третьему просто не найдется места.

Два тупоугольных многоугольника равны:

если равны обе их стороны и угол, находящийся между ними;
если одна сторона и два угла, находящиеся рядом с ней, равны;
если три стороны тупоугольных треугольников имеют равенство.

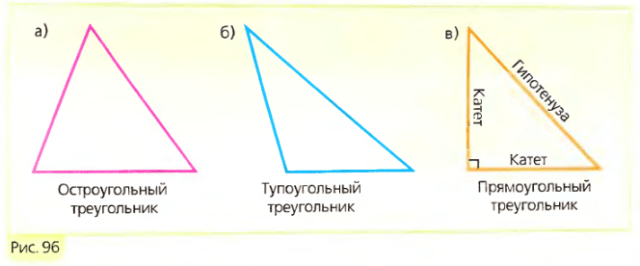
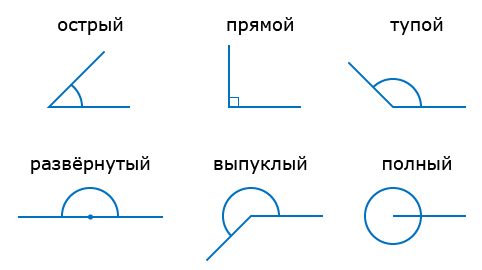
Виды углов: острый, прямой, тупой, полный

Острый угол

Острый угол это угол, значение которого меньше 90 градусов. В произвольном параллелограмме всегда есть два острых и два тупых угла, тогда как в произвольном треугольнике все углы прямые. Если хоть один из углов треугольника прямой или тупой, то фигуру уже нельзя считать произвольной.

Рис. 1. Острый угол.

Прямой угол

Прямой угол очень много значит в геометрии. Прямой угол в параллелограмме, означает, что перед вами квадрат или прямоугольник. Произвольный треугольник, если доказать, что в нем есть прямой угол, сразу же превращается в прямоугольный треугольник, для которого действует больший набор теорем и правил, нежели для произвольного.

Рис. 2. Прямой угол.

Тупой угол

Тупой угол, это угол больше 90 градусов. Это значение очень широко используется в задачах по тригонометрии. Но и в геометрии очень часто можно встретить задачи на тупоугольный треугольник. Считается, что тупоугольный треугольник сложнее воспринимается чисто визуально, но на деле, стоит только привыкнуть и задачи эти уже не будут казаться такими страшными.

Рис. 3. Тупой угол.

Полный угол

Полный угол это угол в 360 градусов. То есть тот самый момент, когда минутная и часовая стрелка совпадает.

Тогда с одной стороны будет полный угол, а с другой угол в 0 градусов. Чисто теоретически и нулевой угол тоже существует, он означает, что стрелки или лучи друг от друга не отклонялись.

Что мы узнали?

Мы узнали, что такое угол, определили виды углов, поговорили о том, какую роль каждый из видов играет в геометрии и привели примеры каждого из них.

Тест по теме

Вопрос 1 из 10

Начать тест(новая вкладка)

Центральный и вписанный угол

Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.

Центральный угол — угол с вершиной в центре окружности. Величина центрального угла равна градусной мере дуги, заключённой между сторонами этого угла.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Величина вписанного угла равна половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол θ равен половине величины центрального угла 2θ, , опирающегося у основания на окружности на ту же самую дугу (розового цвета). То есть угол θ не меняет своей величины от вершины к вершине, взятой на окружности (зелёный и голубой углы). Внешний угол для вписанного с другой стороны угла окружности имеет ту же величину θ (коричневого цвета)

Величина вписанного угла равна половине величины центрального угла, опирающегося у основания на окружности на ту же самую дугу (см. рис.).

Какие углы называются вертикальными? Каким свойством они обладают?

Вертикальные
углы —
два угла, у которых стороны одного
являются продолжениями сторон другого.
Вертикальные углы равны. (Вертикальными
называются углы,
образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).

22.
Какие прямые называются перпендикулярными?

Две
пересекающиеся прямые называются
перпендикулярными
(или взаимно перпендикулярными), если
они образуют четыре прямых угла. Или
Перпендикулярные
прямые это
прямые пересекающиеся под углом 90
градусов. Или Две прямые, образующие
при пересечении прямые углы, называют
перпендикулярными.

23.
Объясните,
какой отрезок называется перпендикуляром,
проведенным из данной точки к данной
прямой. Что такое основание перпендикуляра?

Перпендикуляром
к данной прямой
называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Этот конец
отрезка называется основанием
перпендикуляра.Перпендикуляром
к данной прямой
называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Конец
отрезка, лежащий на данной прямой,
называется основанием перпендикуляра.

24.
Что такое теорема и доказательство
теоремы?

В
математике утверждение, справедливость
которого устанавливается путем
рассуждений, называется теоремой,
а само рассуждение – доказательством
теоремы.

Теоре́ма
— утверждение, для которого в
рассматриваемой теории существует
доказательство (иначе говоря, вывод) .
В отличие от теорем, аксиомами
называются
утверждения, которые, в рамках конкретной
теории, принимаются истинными без всяких
доказательств или обоснований.
Доказательство
—
это утверждение, объясняющее теорему.

Теорема
— такая
гипотеза, которую требуется доказать;Гипотеза
всегда требует доказательства.
Доказательство
— доводы,
подтверждающие действенность, правильность
теоремы.

Общие сведения

Два луча (BA и ВС), выходящие из общей вершины B, образуют на плоскости две области, являющиеся внутренними областями двух плоских углов.

Плоскость, содержащая обе стороны угла, делится углом на две области. Каждая из этих областей, объединённая со сторонами угла, называется (или просто углом, если это не вызывает разночтений). Один из плоских углов (обычно меньший из двух) иногда условно называют внутренним, а другой — внешним. Точки плоского угла, не принадлежащие его сторонам, образуют внутреннюю область плоского угла.

В другом, эквивалентном варианте определения плоским углом называется часть плоскости, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую лежащую в этой плоскости линию (которая называется линией, стягивающей данный плоский угол).

Часто для краткости углом называют также , то есть число, определяющее величину угла.

Кроме наиболее часто встречающихся плоских углов, в качестве углов могут рассматриваться и более общие объекты — фигуры, образованные пересекающимися дугами, полуплоскостями и другими фигурами как в евклидовой, так и в других типах геометрии в метрических пространствах различной размерности.

Определение и измерение

Приступая к изучению, первоначально определяют, что такое угол в планиметрии.

Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:

вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита,
стороны – полупрямые, проведенные из вершины.

Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части:

внутренняя в планиметрии не превышает 180 градусов,
внешняя.

Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.

Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи

Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.

Основные виды

Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.

По величине

Учитывая величину, углы разделяют на:

развернутый,
прямой,
тупой,
острый.

Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.

Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?

180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам. Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.

Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.

Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.

Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.

Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.

Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии основное свойство измерения.

При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.

На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.

Фигуры при пересечении прямых

Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.

Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов.

Элементы в треугольнике

Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними.

Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.

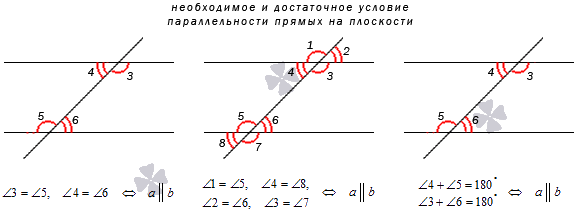
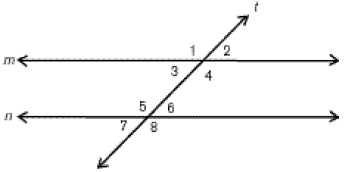
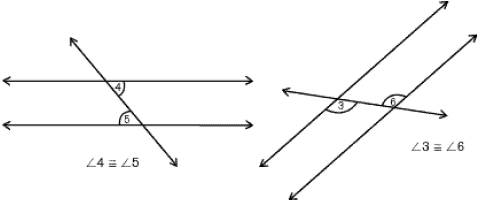
Пересечение двух прямых секущей

Пересечение прямых

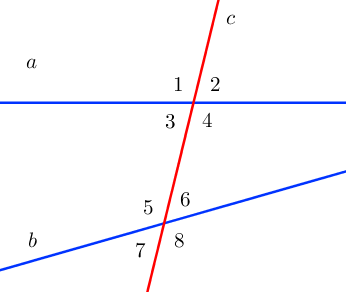
При пересечении двух прямых секущей также образуются углы, которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:

внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5,
внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6,
соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.

В том случае, когда секущая пересекает две параллельные прямые, все эти пары углов имеют определённые свойства:

Внутренние накрест лежащие и соответственные фигуры между собой равны.
Внутренние односторонние элементы в сумме дают 180 градусов.

Изучаем углы в геометрии, их свойства

Виды углов в математике

Гипотенуза

Перейдем непосредственно к гипотенузе треугольника. Гипотенуза – это наибольшая сторона треугольника. Гипотенуза всегда больше любого из катетов, но при этом всегда меньше суммы катетов. Это следствие из теоремы неравенства треугольника.

Теорема гласит: в треугольнике ни одна из сторон не может больше суммы двух других. Существует и вторая формулировка или вторая часть теоремы: в треугольнике напротив большей стороны лежит больший угол и наоборот.

Рис. 2. Прямоугольный треугольник.

В прямоугольном треугольнике большим углом является прямой угол, так как второго прямого угла или тупого угла быть не может по уже названным причинам. Значит напротив прямого угла всегда лежит большая сторона.

Кажется непонятным, почему именно прямоугольный треугольник заслужил отдельное наименование каждой из сторон. На самом деле, в равнобедренном треугольнике стороны так же носят свои названия: боковые стороны и основание. Но именно за катеты и гипотенузы учителя особенно любят ставить двойки. Почему? С одной стороны это дань памяти древним грекам, изобретателям математики. Именно они изучали прямоугольные треугольники и наряду с этими знаниями оставили целый пласт информации, на котором строится современная наука. С другой же стороны существование этих названий значительно упрощает формулировки теорем и тригонометрических тождеств.

Замечательные линии тупоугольного треугольника

Вывод

В этой статье представлены все основные виды углов, которые встречаются в планиметрии и изучаются в седьмом классе. Во всех последующих курсах свойства, касающихся всех рассмотренных элементов, являются основой для дальнейшего изучения геометрии. К примеру, изучая параллелограмм, необходимо будет вспомнить все свойства углов, образованных при пересечении двух параллельных прямых секущей. При изучении особенностей треугольников, необходимо вспомнить, что такое смежные углы. Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.