Теория вероятностей

Вероятность и геометрия

Теория вероятности затрагивает и геометрию. Пусть есть отрезок АВ, в середине которого располагается точка С.

Теперь мы ставим на отрезке АВ случайную точку D. С какой вероятностью она попадет наАС, а с какой на ВС? Так как эти отрезки ничем не отличаются, то можно предположить, что события «попадание точки на АС» и «попадание точки на ВС» являются равновероятными событиями. Так и есть. Их вероятность обоих событий составляет 0,5.

Теперь предположим, что точка С выбрана так, что отрезок АС вдвое короче, чем ВС, то есть ВС = 2 АС:

Чему в этом случае равны вероятности попадания случайной точки D на отрезки АС и ВС? Для ответа на этот вопрос раздели ВС надвое с помощью ещё одной точки K:

Получили три одинаковых отрезка АС, СК и КВ. Раз они одинаковы, то и вероятности случайной точки оказаться на каждом из этих отрезков равны:

Р(АС) = Р(СК) = Р(КВ) = 1/3

Отсюда вероятность попадания точки на ВС равна 2/3:

Р(ВС) = Р(СК) + Р(КВ) = 1/3 + 1/3 =2/3

Получили, что вероятность попадания точки на ВС вдвое выше, чем на АС. И при этом ВС вдвое длиннее. И это не случайно. В общем случае верно следующее правило:

Данное свойство может пригодиться не только в геометрии, но и при решении задач.

Пример. Прохожий пришел на остановку автобуса в случайный момент времени. Он знает, что автобус ходит с интервалом в 40 минут, но не знает, когда отъехал предыдущий автобус. С какой вероятностью автобус придется ждать менее 10 минут?

Решение. Построим схему. На ней время будем откладывать по горизонтальной оси. Отметим точки, соответствующие приезду автобуса (А₁, А₂, А₃, А₄), и точку, соответствующую приходу прохожего (D):

Ясно, что точка D окажется между какими-то двумя точками, которым соответствуют последовательные прибытия поезда.На рисунке это А₂ и А₃. В каком случае время ожидания составить менее 10 минут? В том случае, если точка D окажется на «расстоянии» менее 10 минут от точки А₃, то есть попадет в отрезок ВА₃:

Отрезок ВА₃ вчетверо короче отрезка А₂А₃, поэтому вероятность точку D попасть на него составляет 1/4. Именно такова вероятность, что прохожему придется ждать автобус менее 10 минут.

Ответ: 1/4

В случае, когда точка случайным образом ставится не на отрезке, а на плоской фигуре, то справедливо следующее правило:

Пример. В треугольнике АВС проведена средняя линия NM. С какой вероятностью случайная точка, отмеченная на треугольнике АВС, попадет и на треугольник ANM?

Решение. Средняя линия NM параллельна стороне ВС (это свойство средней линии), а потому равны углы АNM и АВС (соответственные углы при параллельных прямых). Это значит, что треугольники АВС и ANM подобны по двум равным углам. Коэффициент подобия равен 1/2, так как AN/АВ = 1/2. Известно, что отношение площадей подобных фигур равно квадрату их коэффициента подобия, поэтому площадь АMN в 4 раза меньше площади АВМ. По условию точка гарантированно попадает в АВС, то есть вероятность этого события равна 1. Тогда вероятность попадания точки в АNM будет в 4 раза меньше и составит 1/4 .

Ответ:1/4.

Карточная колода

Задачи по теории вероятности бывают и более сложными, для примера возьмем следующее задание. Перед вами колода из тридцати шести карт. Ваша задача — вытянуть две карты подряд, не перемешивая стопку, первая и вторая карты должны быть тузами, масть значения не имеет.

Для начала найдем вероятность того, что первая карта будет тузом, для этого четыре делим на тридцать шесть. Отложили его в сторону. Достаем вторую карту, это будет туз с вероятностью три тридцать пятых. Вероятность второго события зависит от того, какую карту мы вытянули первой, нам интересно, был это туз или нет. Из этого следует, что событие В зависит от события А.

Следующим действием находим вероятность одновременного осуществления, то есть перемножаем А и В. Их произведение находится следующим образом: вероятность одного события умножаем на условную вероятность другого, которую мы вычисляем, предполагая, что первое событие произошло, то есть первой картой мы вытянули туз.

Для того чтобы стало все понятно, дадим обозначение такому элементу, как условная вероятность события. Вычисляется она, предполагая, что событие А произошло. Рассчитывается следующим образом: Р(В/А).

Продолжим решение нашей задачи: Р(А_*В)=Р(А)_*Р(В/А) или Р(А_*В)=Р(В)_*Р(А/В). Вероятность равняется (4/36)_*((3/35)/(4/36). Вычисляем, округляя до сотых. Мы имеем: 0,11_*(0,09/0,11)=0,11_*0,82=0,09. Вероятность того, что мы вытянем два туза подряд, равна девяти сотым. Значение очень мало, из этого следует, что и вероятность происхождения события крайне мала.

Противоположные события

Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.

Это правило действует и в том случае, когда речь идет о неравновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:

0,7 + 0,3 = 1

Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.

Противоположными являются такие события, как:

• падение монеты либо одной стороной вверх (орлом), либо другой (решкой);
• выпадение четного или нечетного числа на шестигранном кубике;
• изготовление рабочим годной или получение бракованной детали.

Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.

Очевидно, что сумма вероятностей противоположных событий равна единице.

Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?

Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице

Р(А) + Р(B) = 1

По условию Р(А) = 0,97. Тогда

0,97 + Р(В) = 1

Перенесем в равенстве слагаемое 0,97 в правую часть и получим:

Р(B) = 1 – 0,97

Р(В) = 0,03

Ответ: 0,03

Частота и вероятность

В мире происходят события, которые можно предсказать. Например, можно предсказать приезд лифта после того, как человек нажмет кнопку его вызова. Астрономы могут заранее предсказывать солнечные и лунные затмения.

Однако нередко нам приходится иметь дело с событиями, результат которых заранее предсказать невозможно. Не получается заранее сказать, упадет ли монетка при подбрасывании орлом вверх, также как нельзя заранее предсказать поломку прибора. Такие события называются случайными.

Случайные события обычно могут произойти только в определенной ситуации. Так, событие «выпадение решки» может произойти только при броске монеты. В математике подбрасывание монетки будет называться испытанием или экспериментом.

Здесь не следует воспринимать термин «эксперимент» как некое научное исследование. Испытанием может оказаться любая жизненная ситуация. Приведем несколько примеров опытов и соответствующих им случайных событий:

• Бросок кубика с 6 гранями – это эксперимент, а выпадение или невыпадение шестерки на нем – это случайное событие.
• Полет самолета – испытание, а отказ двигателя в полете – это случайное событие.
• Ожидание автобуса на остановке в течение 10 минут – эксперимент, а появление или непоявление автобуса в этот промежуток времени – случайное событие.
• Футбольный матч – опыт, а победа в нем команды хозяев или травма одного из игроков – случайное событие.
• Выстрел из винтовки – испытание, а попадание в мишень – случайное событие.
• Изготовление рабочим детали – эксперимент, а получение бракованной детали – случайное событие.

Здесь важно отметить, что для математики не важно, является ли событие по-настоящему случайным. Возможно, что автобус ходит строго по расписанию, и человек, знающий его, точно может определить, через сколько минут он приедет

Но если рядом стоит другой человек, не знающий этой информации, то для него приезд автобуса будет случайным событием.

Предположим, что есть возможность провести какой-то эксперимент множество раз. Например, кубик можно бросить 500 раз. Обозначим это число, количество экспериментов, как n. В ходе серии этих бросков шестерка выпала, например, 85 раз. Обозначим эту величину, количество произошедших случайных событий, как m. Само событие «выпадение шестерки» обозначим как А. Тогда отношение m/n будет называться частотой случайного события А. В данном случае частота события А равна

85/500 = 0,17

Наблюдения показывают, что если условия экспериментов примерно одинаковы, а их число велико, то частота одного и того же события будет примерно одинаковой. Чем больше число испытаний, тем обычно ближе частота события к некоторому постоянному числу. Это число и называют вероятностью случайного события А.

Грубо говоря, частота и вероятность событий – это примерно одно и то же. Частоту определяют на практике, входе эксперимента, а вероятность можно рассчитать аналитически.

Вероятность – это величина, которая характеризует возможность события произойти. Если она близка к единице, то событие, скорее всего, произойдет. Если она близка к нулю, то событие, скорее всего, не случится. Для обозначения вероятности используется буква Р. Если надо указать вероятность конкретного события А, то его записывают как Р(А).

Вероятность – это безразмерная величина, то есть для нее нет никакой единицы измерения. Она может принимать значение от 0 до 1. Иногда на практике ее указывают в . Например, вероятность 0,5 означает 50%. Чтобы перевести вероятность в проценты, ее надо просто умножить на 100.

Случайные события

Изучая элементы теории вероятности, особое внимание стоит уделить именно данному виду события. Именно их и изучает данная наука

В результате опыта может что-то произойти или нет. Кроме этого, испытание может проводиться неограниченное количество раз. Яркими примерами могут служить:

• Бросок монеты – это опыт, или испытание, выпадение орла – это событие.
• Вытягивание мячика из мешка вслепую – испытание, попался красный шар – это событие и так далее.

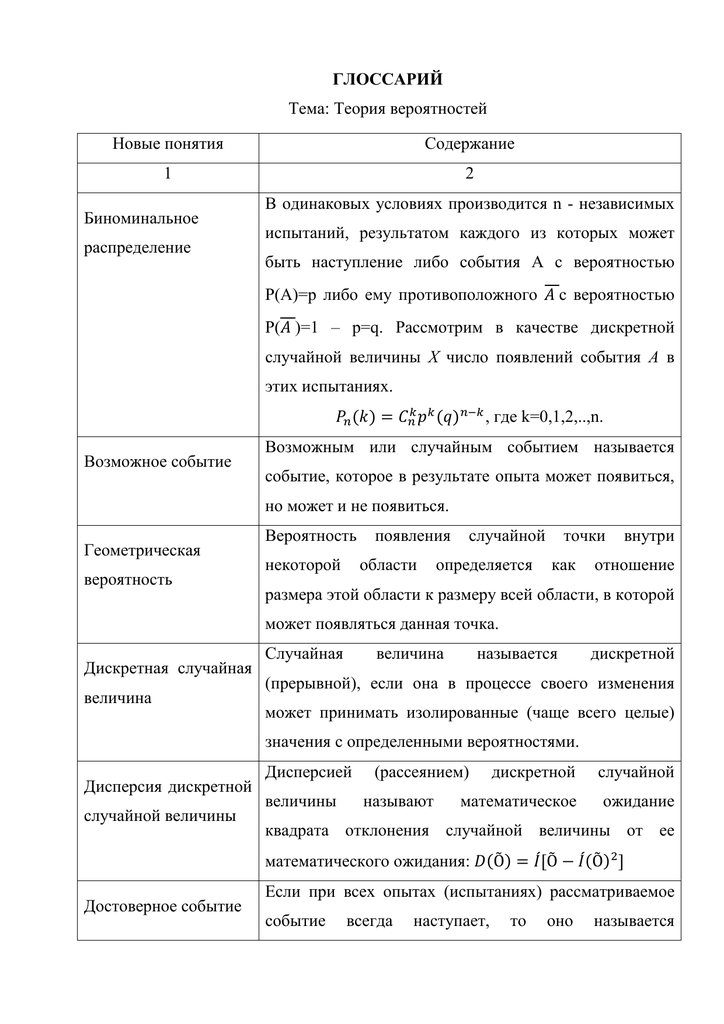
Таких примеров может быть неограниченное количество, но, в общем, суть должна быть понятна. Для обобщения и систематизирования полученных знаний о событиях приведена таблица. Теория вероятности изучает только последний вид из всех представленных.

название	определение	пример
Достоверные	События, происходящие со стопроцентной гарантией при соблюдении некоторых условий.	Поступление в учебное заведение при хорошей сдаче вступительного экзамена.
Невозможные	События, которые никогда не произойдут ни при каких условиях.	Идет снег при температуре воздуха плюс тридцать градусов по Цельсию.
Случайные	Событие, которое может произойти или нет в ходе проведения опыта/испытания.	Попадание или промах при бросании баскетбольного мяча в кольцо.

Сходимость последовательностей случайных величин

Отметим, что видов сходимости несколько:

• Последовательность случайных величин сходима по вероятности.
• Почти невозможное.
• Среднеквадратическая сходимость.
• Сходимость по распределению.

Так, с лету, очень тяжело вникнуть в суть. Приведем определения, которые помогут разобраться в данной теме. Для начала первый вид. Последовательность называют сходимой по вероятности, если соблюдено следующее условие: n стремится к бесконечности, число, к которому стремится последовательность, больше нуля и приближена к единице .

Переходим к следующему виду, почти наверное. Говорят, что последовательность сходится почти наверное к случайной величине при n, стремящейся к бесконечности, и Р, стремящейся к величине, приближенной к единице.

Следующий тип – это сходимость среднеквадратическая. При использовании СК-сходимости изучение векторных случайных процессов сводится к изучению их координатных случайных процессов.

Остался последний тип, давайте разберем кратко и его, чтобы переходить непосредственно к решению задач. Сходимость по распределению имеет и еще одно название — «слабое», далее поясним, почему. Слабая сходимость — это сходимость функций распределения во всех точках непрерывности предельной функции распределения.

Обязательно выполним обещание: слабая сходимость отличается от всех вышеперечисленных тем, что случайная величина не определена на вероятностном пространстве. Это возможно потому, что условие формируется исключительно с использованием функций распределения.

Условная вероятность

Иногда можно перемножать вероятности событий, не являющихся в полном смысле слова независимыми. Пусть для того, чтобы произошло событие А, необходимо, чтобы последовательно произошли В и С. В зависимости от того, произошло ли В, вероятность С может отличаться. Например, в урне лежат 4 шарика – 2 красных и 2 желтых. Предположим, что произошло событие В – был вытащен красный шар. Его вероятность равна 0,5. Чему тогда равна вероятность события С – вытаскивания желтого шарика? В урне осталось 3 шара, из них 2 желтых, поэтому Р(С) = 2/3.

С другой стороны, пусть В не произошло, то есть первым был вынут желтый шар. Чему тогда равна вероятность С? В урне снова 3 шарика, но лишь 1 из них желтый. Следовательно, Р(С) = 1/3. Получается, что в зависимости от того, случилось ли В, вероятность Р(С) принимает разные значения. В математике такую вероятность называют условной.

Обозначается она так:

Р(С|B).

Первая буква в скобках соответствует событию, для которого указываем вероятность, а вторая буква – событию, которое является условием для С.

Если событие А произойдет тогда, когда свершится сначала В, а потом С, то вероятность А также можно найти с помощью умножения

Р(А) = Р(В)•Р(С|B)

Пример. В урне находится 52 шара, из них на 4 написана буква Т. Из урны последовательно вынимаются два шара. Какова вероятность, что на обоих вытащенных шарах будет буква Т?

Решение. Так как в урне 52 шара, и лишь на 4 есть буква Т, то шанс на то, что первым вытащат именно шар с буквой Т, равен 4/52 = 1/13. Если это событие произошло, то в урне остался 51 шар, и лишь на трех будет находиться нужный символ. Тогда вероятность появления шара с буквой Т составит 3/51 = 1/17. Общая же вероятность появления 2 таких шаров подряд найдется как произведение этих вероятностей:

Р = (1/13)•(1/17) = 1/221 ≈ 0,004525

Эту вероятность можно рассчитать и иначе, по аналогии с задачей про бракованные велосипеды, которая приведена выше. Подсчитаем, сколькими способами можно выбрать 2 шара из 52:

Но всего 6 способами можно выбрать 2 шара из 4:

Поделив число благоприятных исходов на их общее количество, получим искомую вероятность:

Р = 6/1326 = 1/221.

Ответ: 1/221

Пример. Известно, что вероятность мужчины дожить до 90 лет составляет 5,126%, а до 95 лет – 1,326%. С какой вероятностью мужчина, которому уже сейчас 90 лет, доживет до 95 лет?

Решение. Пусть А – это дожитие до 95 лет, С – дожитие 90-летнего мужчины до 95 лет, В – дожитие до 90 лет. Чтобы отпраздновать 95-летие, человек сначала должен отметить 90-летний юбилей, а потом ещё прожить 5 лет. Другими словами, чтобы случилось А, сначала должно случиться В, а потом событие С при условии В. То есть можно записать

Р(А) = Р(В)•Р(С|B)

По условию Р(А) = 0,01326, а Р(В) = 0,05126. Зная это, легко найдем Р(С|B):

Р(А) = Р(В)•Р(С|B)

0,01326 = 0,05126•Р(С|B)

Р(С|B) = 0,01326/0,05126 ≈ 0,2587

Это и есть вероятность мужчины, отметившего 90-ый день рождения, дожить до 95 лет.

Ответ: 0,2587