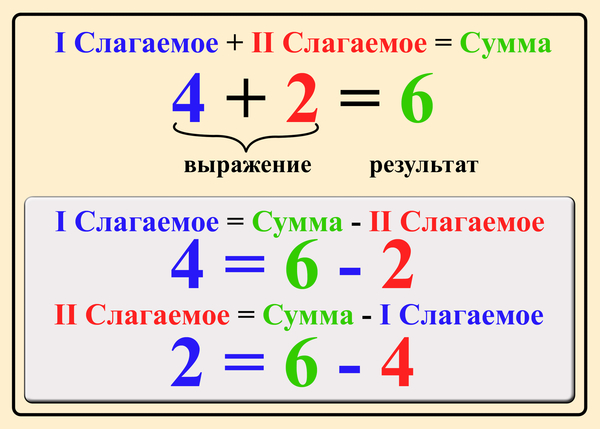
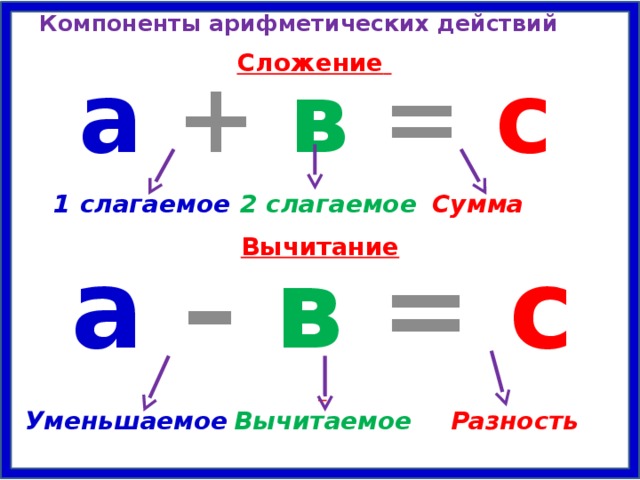
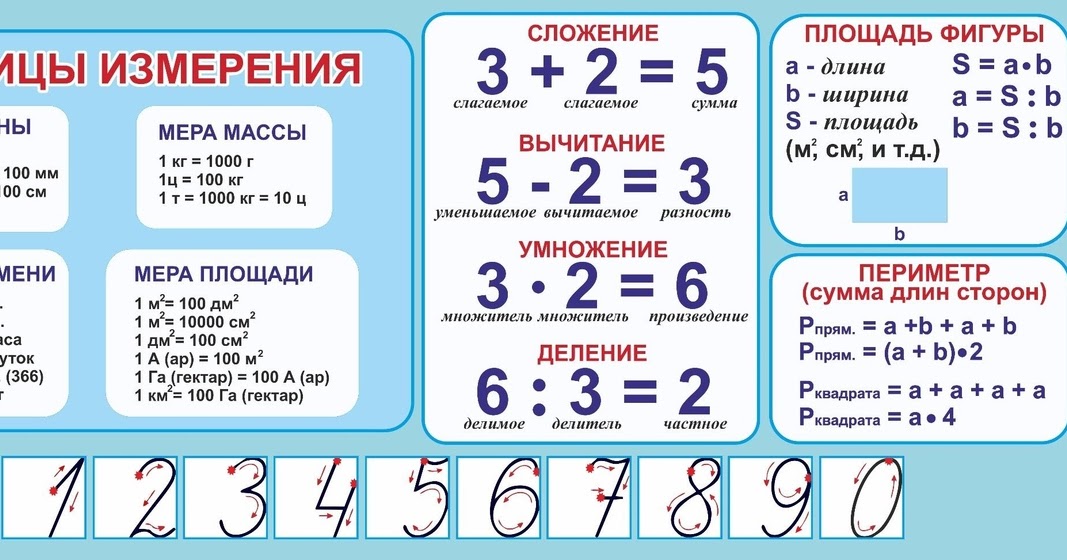
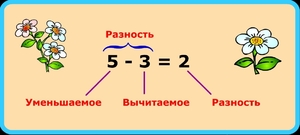
Вычитаемое уменьшаемое разность – правило: что это такое и как их найти
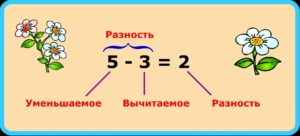
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п.
Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова «вычитаемое», «уменьшаемое», «разность».
Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
Термины
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами;
- это показатель того, насколько одно количество больше или меньше другого;
- это результат, полученный при выполнении вычитания — такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю
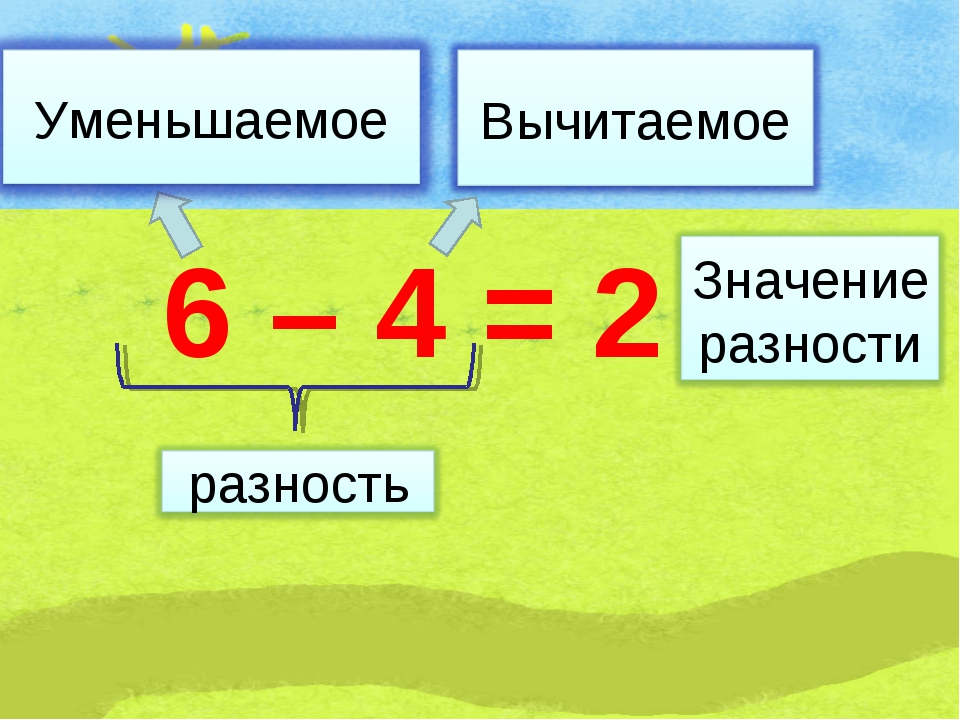
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | — | 11 | = | 7 |
| 14 | — | 5 | = | 9 |
| 26 | — | 22 | = | 4 |
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
! Уроки математики: умножение на ноль — главное правило
Как найти уменьшаемое
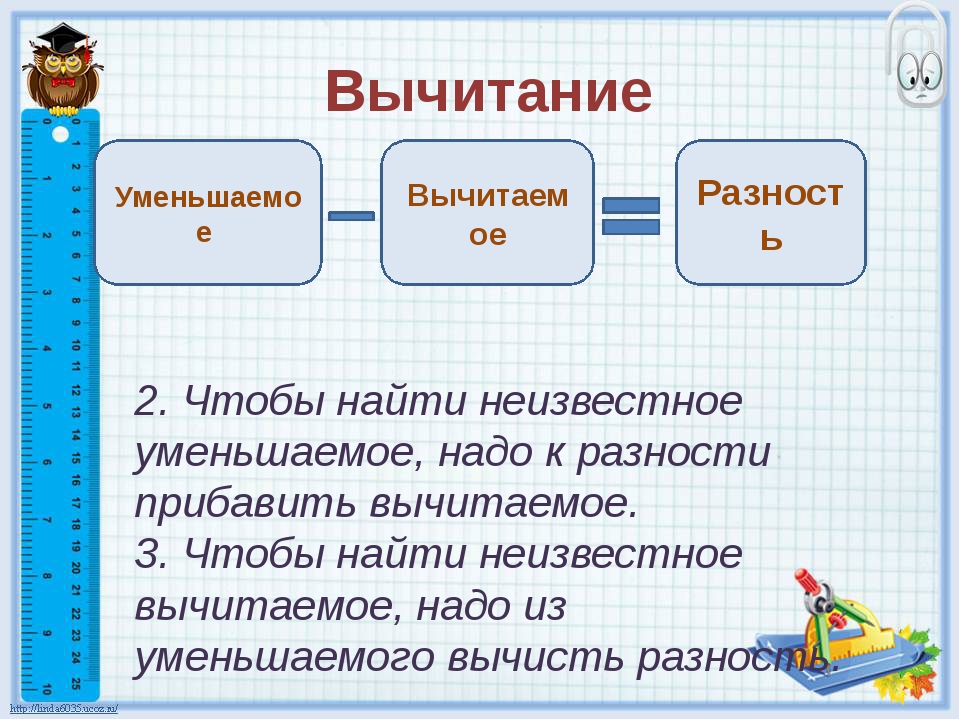
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
Искомое находится путем сложения известных элементов:
Так же и во всех подобных случаях:
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
По тому же правилу решаются и другие подобные примеры.
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
! Как разложить на множители квадратный трехчлен: формула
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных.
Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих.
Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
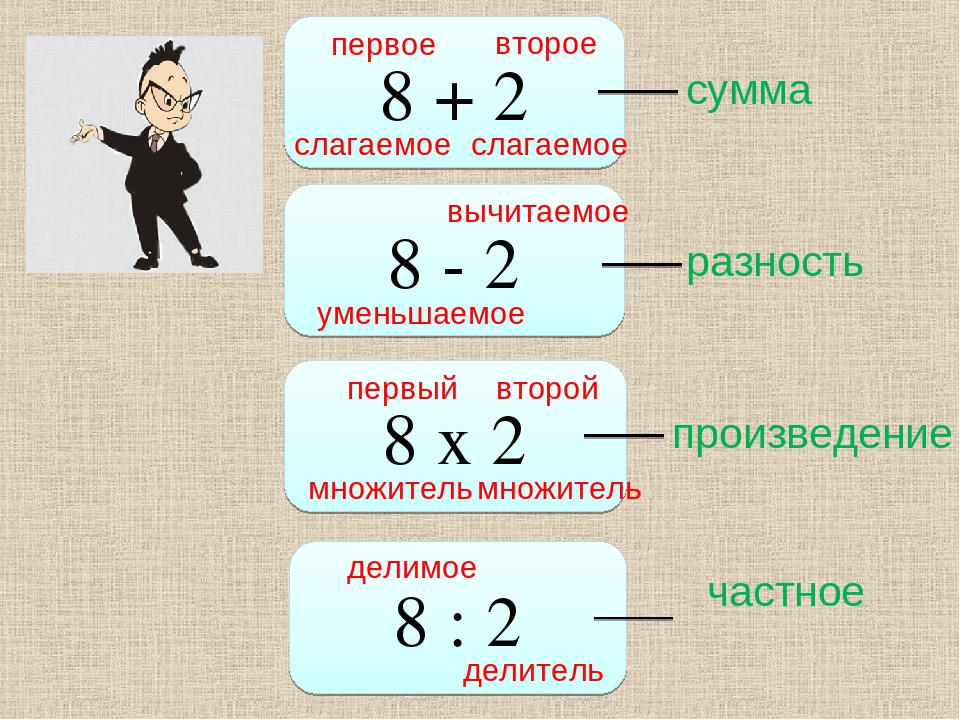
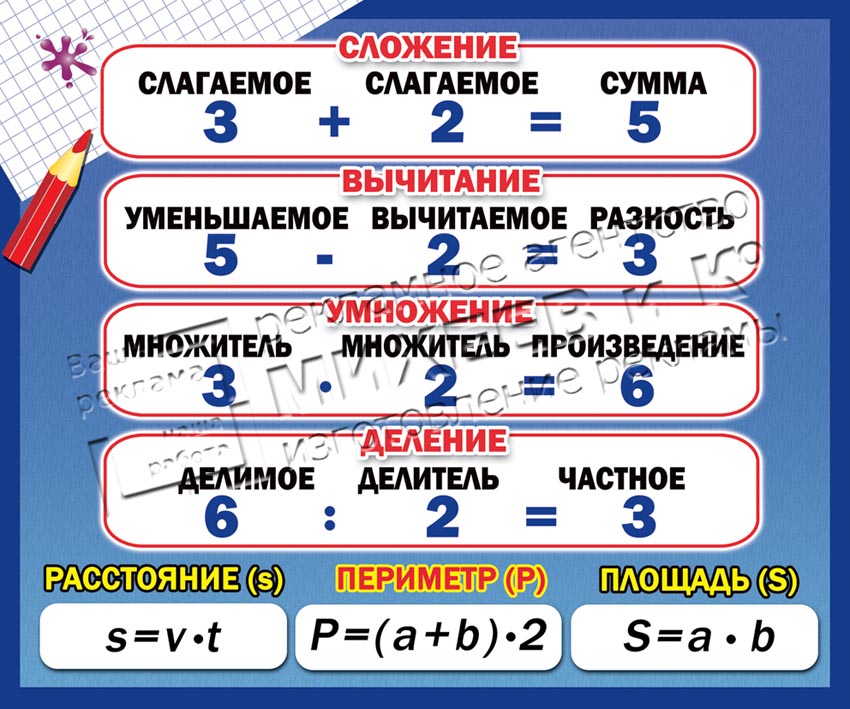
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Вот такая интересная арифметика.
Что значит число уменьшаемое, число вычитаемое и разность чисел?

Натуральные числа
Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.
Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница». А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами
Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.
Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:
8 – 5 = 3
То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».
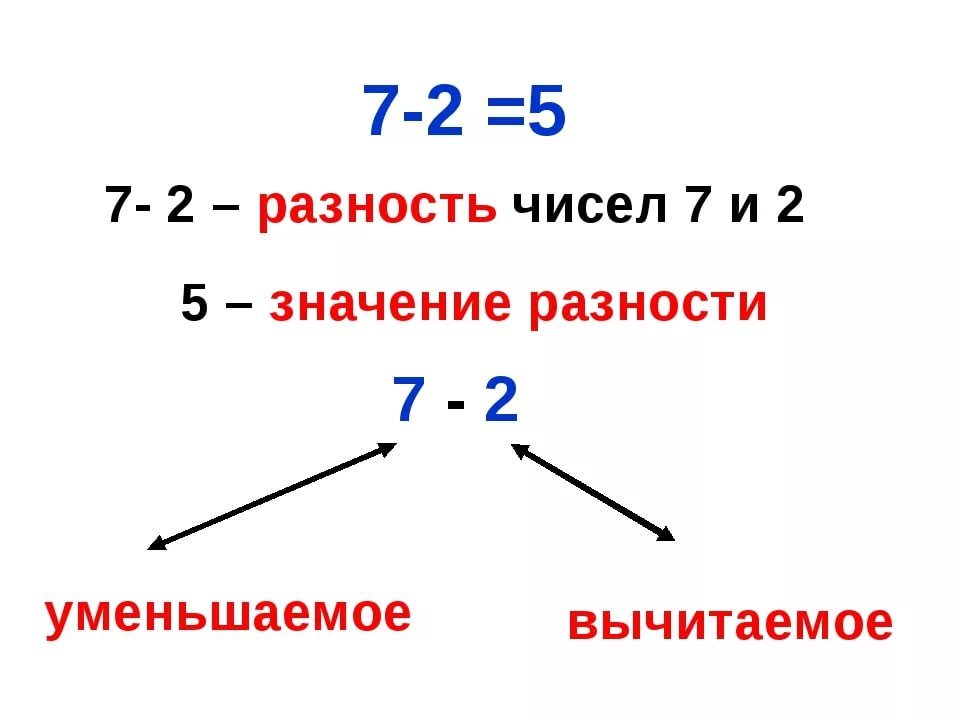
Натуральные числа
Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.
Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.
разность — это… Что такое разность?
common difference, difference матем., differential, remainder, residual
* * *
ра́зность ж.difference
ра́зность долго́т ме́ста и географи́ческого ме́ста — the difference in longitude between the observer and the geographical position of the observer
найти́ ра́зность чи́сел A и B — take the difference of A and B
ра́зность напряже́ния се́ти и потреби́теля — the difference in voltage between the mains and load
ра́зность арифмети́ческой прогре́ссии — common difference
ра́зность взгля́дов геод. — difference in length of sight
втора́я ра́зность мат. — second (order) difference
ра́зность глуби́н модуля́ции ав. — difference in depth modulation, DDM
ра́зность давле́ний — pressure difference
ра́зность для интерполи́рования вперё́д мат. — forward difference
ра́зность для интерполи́рования наза́д мат. — backward difference
ра́зность долго́т навиг. — difference of longitude, D. Long.
коне́чная ра́зность мат. — finite difference
ле́вая ра́зность мат. — backward difference
ра́зность магни́тных потенциа́лов — magnetic potential difference
ра́зность меридиа́нных часте́й — meridional difference of latitude
ра́зность населё́нностей полупр. — population difference
обра́тная ра́зность мат. — reciprocal difference
ра́зность паралла́ксов — parallax difference
пе́рвая ра́зность мат. — first difference
ра́зность потенциа́лов — potential difference
ра́зность потенциа́лов на сопротивле́нии, в це́пи и т. п. — a potential difference across a resistor, circuit, etc.
проходи́ть ра́зность потенциа́лов () … — fall through a potential difference of …
пра́вая ра́зность мат. — forward difference
психрометри́ческая ра́зность — wet-bulb depression, psychrometric difference
разделё́нная ра́зность мат. — divided difference, difference quotient
ра́зность фаз — difference in phase, phase difference
ра́зность хо́да луча́ () физ., радио — path-length difference
ра́зность широ́т навиг. — difference of lattitude, D. Lat.
* * *
difference
Русско-английский политехнический словарь. Академик.ру. 2011.
Что такое разность чисел в математике?
Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.
Вычитание
Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.
По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций. Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?
Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.
Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.
Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.
Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.
Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?
В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.
Особенности вычитания отрицательных чисел
Также бывают ситуации, когда второе число, по сути, меньше первого, однако является отрицательным. Например, рассмотрим выражение 7-(-4). Проще всего разобраться с этой операцией путем превращения комбинации –(- в обычный плюс. Знаки даже внешне напоминают его. В связи с этим, результатом выражения, то есть разницей чисел, будет 11.
Если оба числа являются отрицательными, то вычитание будет происходить следующим образом.
-6-(-7): минус у первого числа сохранится, а комбинация из двух последующих минусов превратится в плюс. Таким образом, необходимо понять, сколько будет -6+7. Разницу найти нетрудно – она равняется единице.
Если же необходимо вычесть положительное число из отрицательного, то выражение можно представить как простое сложение, а затем подписать к результату минус. Например, -3-4 (4 – положительное число), в результате даст -7.
Правило встречается в следующих упражнениях:
1 класс
Страница 30,
Моро, Волкова, Степанова, Учебник, 2 часть
Страница 49,
Моро, Волкова, Степанова, Учебник, 2 часть
Страница 56,
Моро, Волкова, Степанова, Учебник, 2 часть
Страница 69,
Моро, Волкова, Степанова, Учебник, 2 часть
Страница 90,
Моро, Волкова, Степанова, Учебник, 2 часть
Страница 109,
Моро, Волкова, Степанова, Учебник, 2 часть
Страница 5,
Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 19,
Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 27,
Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 39,
Моро, Волкова, Рабочая тетрадь, 2 часть
2 класс
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 66,
Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 15. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы
Страница 46. Вариант 1. № 3,
Моро, Волкова, Проверочные работы
Страница 58. Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 80,
Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 57,
Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 72,
Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 78. Вариант 1. Тест 2,
Моро, Волкова, Проверочные работы
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
4 класс
Страница 7,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 68,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 8,
Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 25,
Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 41. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Математика для блондинок
 Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых,
- произведение — умножением множителей,
- частное — делением делимого на делитель.
Вот такая интересная арифметика.
Что такое сумма, и как ее найти
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых , эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
РАЗНОСТЬ, разности, жен. 1. Число, составляющее остаток в вычитании (мат.). Уменьшаемое равно вычитаемому плюс разность. 2. только ед. отвлеч. сущ. к разный в 1 знач.; различие несходство (книжн.). Разность взглядов. Разность характеров. ❖ Разные … Толковый словарь Ушакова
разность
— См. разница… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. разность избыток, разница; отличие, различие, разрыв, несходство; разнокалиберность, перепад, сальдо, марджин, натяг,… … Словарь синонимов
РАЗНОСТЬ
— (difference) Изменение значения какой либо переменной между фиксированными моментами времени. Если xt – значение переменной х во время t, то первая разность определяется как Δxt=xt–xt–1. Вторая разность равна первой разнице Δxt, минус первая… … Экономический словарь
РАЗНОСТЬ
— (1) потенциалов (напряжение (см. (2))) количественная характеристика электрического поля неподвижных электрических зарядов () между двумя его точками, равная работе электрического поля по перемещению единичного положительного заряда из одной… … Большая политехническая энциклопедия
РАЗНОСТЬ
— РАЗНОСТЬ, разнота и пр. см. разный. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
РАЗНОСТЬ
— результат вычитания … Большой Энциклопедический словарь
РАЗНОСТЬ
— РАЗНОСТЬ, и, жен. 1. см. разный. 2. Результат, итог вычитания. | прил. разностный, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
разность
— — Тематики электротехника, основные понятия EN differential … Справочник технического переводчика
Разность
— Разность многозначный термин: результат вычитания. Разность (минералогия) (например, «среднезернистые разности» или «мелоподобные разности») Разность потенциалов … Википедия
разность
— и; ж. 1. к Разный (1 зн.); различие. Р. убеждений, взглядов. Обнаружить р. в подходах к историческим фактам. // Различие между двумя сравниваемыми величинами в числовом выражении. Р. высот над уровнем моря. Р. температур. Р. уровней воды. Р. в… … Энциклопедический словарь
Книги
- Комплект таблиц. Алгебра. 7 класс. 15 таблиц + методика , . Таблицы отпечатаны на плотном полиграфическом картоне размером 680 х 980 мм.
В комплект входит брошюра с методическими рекомендациями для учителя.
Учебный альбом из 15 листов. Выражения.… Купить за 3480 руб - Распределенная во времени «разность разностей» на примере оценки отдачи от дополнительного профессионального обучения , А. В. Аистов. В работе представлена эконометрическая модель, описывающая распределение во времени эффекта воздействия, построенная на основе методологии «разность разностей». Модель позволила…
Разностью принято называть результат, полученный путем вычитания меньшего числа из большего. В данном случае, первое число из которого вычитается другое, получает название уменьшаемое (ведь именно его мы уменьшаем в процессе). Второе же, вычитаемое из первого числа, так и называется вычитаемым. В сумме с разностью вычитаемое составляет собой уменьшаемое, а разница между уменьшаемым и разностью становится вычитаемым. В случаях, когда вычитаемое превышает собой уменьшаемое, разность чисел становится отрицательной.
Существует несколько формул разности:
- формула разности a-b = с
- формула разности квадратов a 2 — b 2 = (a — b)*(a + b)
- формула разности кубов a 3 — b 3 = (a — b)*(a 2 + ab + b 2)
- формула разности потенциалов U=Aq
- формула квадрата разности (a — b) 2 = a 2 — 2ab + b 2
- формула куба разности (a — b) 3 = a 3 — 3a2b + 3ab 2 — b 3