Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Вместо скучных учебников ученики проходят интерактивные задания с автоматической проверкой, рисуют вместе с учителем на онлайн-доске и задают вопросы, которые бывает неловко спросить перед всем классом.
Дюймы против мм. Откуда путаница и когда необходима таблица соответствия

Трубы, диаметр которых обозначается дюймами (1″, 2″
) и/или долями дюймов (1/2″, 3/4″
), являются общепринятым стандартом в водо — и водогазоснабжении.
Как правило монтаж дюймовых труб проходит без затруднений, но при их замене на трубы из пластика, меди и нержавеющей стали возникает проблема — несоответствие размера обозначенного дюйма (33,5 мм
) к его реальному размеру (25,4 мм
).
Обычно этот факт вызывает недоумение, но если глубже заглянуть в процессы происходящие в трубе, то логика несоответствия размеров становится очевидна и непрофессионалу. Все довольно просто — читайте дальше.
Дело в том, что при создании водного потока ключевую роль играет не внешний, а внутренний диаметр и по этой причине для обозначения используется именно он.
Однако несоответствие обозначаемых и метрических дюймов все равно остается, т. к. внутренний диаметр стандартной трубы составляет 27,1 мм
, а усиленной — 25,5 мм
. Последнее значение стоит довольно близко к равенству 1″»=25,4
но все же им не является.
Разгадка состоит в том, что для обозначения размера труб применяется номинальный, округленный до стандартного значения диаметр (условный проход Dy
). Величина условного прохода подбирается так, чтобы пропускная способность трубопровода увеличивалась от 40 до 60%
в зависимости от роста величины индекса.
В ситуациях с пластиковыми трубами для решения проблемы несоответствующих размеров используются переходные элементы. При необходимости заменить или состыковать дюймовые трубы с трубами, выполненными по реальным метрическим размерам — из меди, нержавейки, алюминия, следует брать во внимания и наружный, и внутренний диаметры.

Таблица соответствия условного прохода дюймам
| Ду | Дюймы | Ду | Дюймы | Ду | Дюймы |
| 6 | 1/8″ | 150 | 6″ | 900 | 36″ |
| 8 | 1/4″ | 175 | 7″ | 1000 | 40″ |
| 10 | 3/8″ | 200 | 8″ | 1050 | 42″ |
| 15 | 1/2″ | 225 | 9″ | 1100 | 44″ |
| 20 | 3/4″ | 250 | 10″ | 1200 | 48″ |
| 25 | 1″ | 275 | 11″ | 1300 | 52″ |
| 32 | 1(1/4)» | 300 | 12″ | 1400 | 56″ |
| 40 | 1(1/2)» | 350 | 14″ | 1500 | 60″ |
| 50 | 2″ | 400 | 16″ | 1600 | 64″ |
| 65 | 2(1/2)» | 450 | 18″ | 1700 | 68″ |
| 80 | 3″ | 500 | 20″ | 1800 | 72″ |
| 90 | 3(1/2)» | 600 | 24″ | 1900 | 76″ |
| 100 | 4″ | 700 | 28″ | 2000 | 80″ |
| 125 | 5″ | 800 | 32″ | 2200 | 88″ |

Таблица соответствия диаметра условного прохода, резьбы и наружных диаметров трубопровода в дюймах и мм.
|
Условный проход трубы Dy. мм |
Диаметр резьбы G». дюйм |
Наружный диаметр трубы Dn. мм |
||
|
Трубы стапьные водо/водогазoпроводные ГОСТ 3263-75 |
Трубы стальные эпектросварные прямошовные ГОСТ 10704-91. Трубы стальные бесшовные горячедеформированные ГОСТ 8732-78. ГОСТ 8731-74 (ОТ 20 ДО 530 мл) |
Полимерная труба. ПЭ, ПП, ПВХ |
||
ГОСТ
— государственый стандарт, используемый в тепло — газо — нефте — трубопроводах
ISO
— стандарт обозанчения диаметров, используется в сантехнических инженерных системах
SMS
— шведский стандарт диаметров труб и запорной арматуры
DIN / EN
— основной евросортамент для стальных труб по DIN2448 / DIN2458
ДУ (Dy)
— условный проход
Таблицы с размерами полипропиленовых труб представлены в следующей статье >>>
Таблица соответствия условного диаметра труб с международной маркировкой
|
ГОСТ |
ISO дюйм |
ISO мм |
SMS мм |
DIN мм |
ДУ |
| 8 | 1/8 | 10,30 | 5 | ||
| 10 | 1/4 | 13,70 | 6,35 | 8 | |
| 12 | 3/8 | 17,20 | 9,54 | 12,00 | 10 |
| 18 | 1/2 | 21,30 | 12,70 | 18,00 | 15 |
| 25 | 3/4 | 26,90 | 19,05 | 23(23) | 20 |
| 32 | 1 | 33,70 | 25,00 | 28,00 | 25 |
| 38 | 1 ¼ | 42,40 | 31,75 | 34(35) | 32 |
| 45 | 1 ½ | 48,30 | 38,00 | 40,43 | 40 |
| 57 | 2 | 60,30 | 50,80 | 52,53 | 50 |
| 76 | 2 ½ | 76,10 | 63,50 | 70,00 | 65 |
| 89 | 3 | 88,90 | 76,10 | 84,85 | 80 |
| 108 | 4 | 114,30 | 101,60 | 104,00 | 100 |
| 133 | 5 | 139,70 | 129,00 | 129,00 | 125 |
| 159 | 6 | 168,30 | 154,00 | 154,00 | 150 |
| 219 | 8 | 219,00 | 204,00 | 204,00 | 200 |
| 273 | 10 | 273,00 | 254,00 | 254,00 | 250 |
Диаметры и другие характеристики трубы из нержавеющей стали
|
Проход, мм |
Диаметр наружн., мм |
Толщина стенок, мм |
Масса 1 м трубы (кг) |
||
| стандартных | усиленных | стандартных | усиленных | ||
| 10 | 17 | 2.2 | 2.8 | 0.61 | 0.74 |
| 15 | 21.3 | 2.8 | 3.2 | 1.28 | 1.43 |
| 20 | 26.8 | 2.8 | 3.2 | 1.66 | 1.86 |
| 25 | 33.5 | 3.2 | 4 | 2.39 | 2.91 |
| 32 | 42.3 | 3.2 | 4 | 3.09 | 3.78 |
| 40 | 48 | 3.5 | 4 | 3.84 | 4.34 |
| 50 | 60 | 3.5 | 4.5 | 4.88 | 6.16 |
| 65 | 75.5 | 4 | 4.5 | 7.05 | 7.88 |
| 80 | 88.5 | 4 | 4.5 | 8.34 | 9.32 |
| 100 | 114 | 4.5 | 5 | 12.15 | 13.44 |
| 125 | 140 | 4.5 | 5.5 | 15.04 | 18.24 |
| 150 | 165 | 4.5 | 5.5 | 17.81 | 21.63 |
? Читайте также. Всё по теме
Как было измерена длина окружности планеты
Для измерения земной окружности существуют сложные инструменты. Однако это можно сделать и с применением знаний из геометрии. Эти вычисления впервые проделал древнегреческий учёный Эратосфен.
Древние предания гласят, как в день летного солнцестояния, когда Солнце расположено выше всего над горизонтом, они видели, что окружающие предметы совсем не отбрасывают тень. В самых глубоких колодцах дно освещалось. Это явление наблюдалось в Сиене, в 500 милях на юг от египетской Александрии.
Эратосфену было известно, что в Александрии в двадцатых числах июня предметы всегда отбрасывают тень, а Солнце не освещает дно глубоких колодцев. Измерив длину тени от обелиска (высота ему была известной), Эратосфен определил, что Сиена находится на 7 градусов южнее Александрии. Это отличие ещё раз доказывало тот факт, что наша планета круглая. Если бы это было не так, то Солнце одновременно во всех пунктах планеты было бы в зените. А измерить диаметр, исходя из окружности легко, зная число π, не составляет труда. Радиус Земли будет в 2 раза меньше диаметра.
Для измерения зенитного расстояния древнегреческий ученый применил скафис, или солнечные часы. Основа этого прибора – чаша в виде полусферы, в центре которой находится острый стержень. На внутренней поверхности чаши имеются деления. Величина тени в астрономический день солнцестояния давало величину дневного светила в зените. С помощью этого же прибора удавалось узнать высоту Солнца в самый короткий день года.
Полученная величина угла являла собой одну пятидесятую часть окружности в 360 градусов. Продолжая свои вычисления, Эратосфен умножил расстояние от Александрии до Сиены на 50. Длина окружности у него была равной 25 тысячам миль (или 40 тысяч 75 километров). Погрешность была допущена из-за того, что учёный не учёл того, что Сиена и Александрия находятся на разных меридианах и применял приближенное расстояния между указанными городами. Для тех времён такое измерение было настоящим научным триумфом.
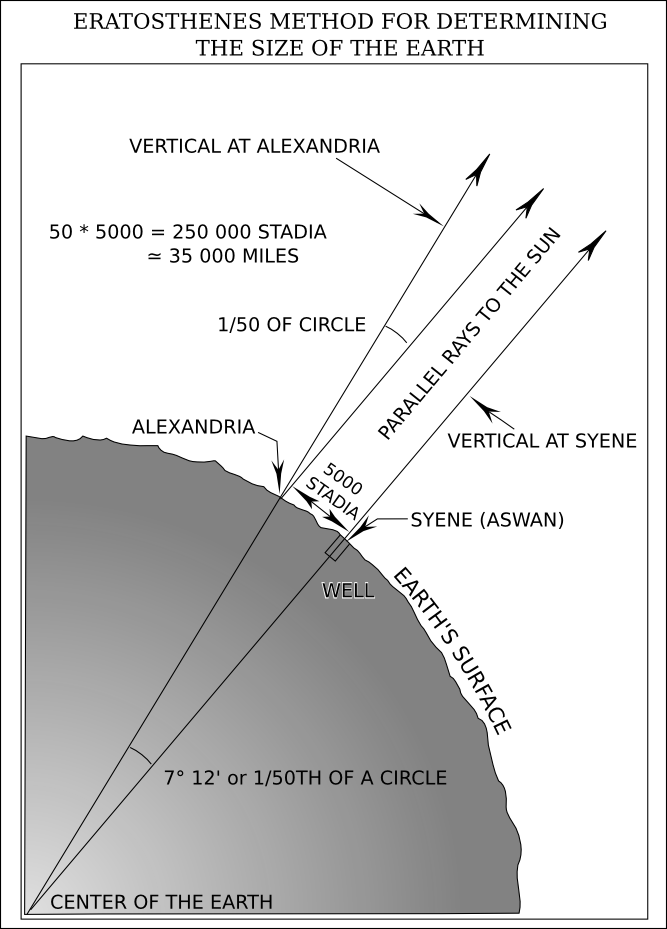 Метод Эратосфена для определения радиуса и окружности Земли.
Метод Эратосфена для определения радиуса и окружности Земли.
Кругосветное путешествие Фернана Магеллана позволило ещё раз убедиться в том, что наша планета кругла и что её окружность превышает 40 тыс. км. Так что утверждение о «плоской» Земле были полностью опровергнуты.
Чтобы пройти свыше 40 тысяч километров по экватору пешком, следует затратить 333 суток при условии, что пешеход не будет останавливаться и скорость будет 5 км в час. Если же человек будет проходить экватор всего по 6 часов в день с такой же скоростью, то на такое пешее путешествие ему придётся потратить около 1 330 суток или 3,6 года.
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
- Диаметром множества M{\displaystyle M}, лежащего в метрическом пространстве с метрикой ρ{\displaystyle \rho }, называется величина (supx,y∈Mρ(x,y)){\displaystyle (\sup _{x,y\in M}\rho (x,y))}. Например, диаметр n-размерного гиперкуба со стороной s равен
- d=s⋅n{\displaystyle d=s\cdot {\sqrt {n}}}.
Гиперонимы к слову диаметр
-
- длина
- отрезок
- поперечник
- расстояние
- хорда
Диаметр
в изначальном значении – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка.
Диаметр равен двум радиусам: D = 2R
.
Радиус
(лат. radius – спица колеса, луч) – отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Радиус составляет половину диаметра
.
Диаметр
– это хорда (отрезок, соединяющий две точки на окружности (сфере, поверхности шара) и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через центр этой окружности; такая хорда имеет максимальную длину.
В круге все диаметры равны и делят круг и все перпендикулярные хорды пополам. В эллипсе лишь два диаметра: самый большой и самый малый, перпендикулярные между собой, они делят эллипс пополам. В шаре, сфероиде, эллипсоиде и подобным геометрическим фигурам, диаметр = плоскость, проходит через центр и делит все перпендикулярные плоскости пополам.
Какую трубу считать малой — средней -большой?
Даже в серьезных источниках мне приходилось наблюдать фразы типа: «Берем любую трубу среднего диаметра и…», но какой этот средний диаметр никто не указывает.
Чтобы разобраться, стоит сначала понять на какой диаметр нужно ориентироваться: он может быть внутренним и внешним. Первый важен при расчете транспортировочной способности воды или газа, а второй для определения возможности выдерживать механические нагрузки.
Внешние диаметры:
От 426 мм считается большим;
102-246 называют средним;
5-102 классифицируется, как маленький.
Что касается внутреннего диаметра, то лучше заглянуть в специальную таблицу(см. выше).
Посадочный диаметр – что означает
Чаще всего, водители сталкиваются с внутренним диаметром. Обычно его называют – посадочный диаметр шины. Показывает он допустимые параметры колесного диска, на который подходит покрышка.
Указывается параметр в типоразмере на боковине покрышки. В качестве примера возьмем 205/65 R15. Диаметр здесь идет сразу после буквы R, он указан в дюймах. Конкретно тут это 15 дюймов или 381 миллиметров.
При выборе автопокрышки следует учитывать, посадочный диаметр должен точно совпадать с колесным диском. Если будет больше, смонтировать колесо не получится. При посадочном размере шины, меньшем чем диск, вероятно покрышка будет повреждена при монтаже.
Применение и формула
Зная диаметр окружности, можно осуществлять строительство жилых домов, развлекательных центров, супермаркетов. Инженеры-конструкторы, занимающиеся разработкой разнообразных машин, агрегатов, механизмов, постоянно сталкиваются с подобными вычислениями. Какова формула диаметра данной кривой? Вычерчивают ее с помощью циркуля. В математике применяется прием косвенного вычисления длины окружности.
Самым простым способом является использование радиуса. Диаметр вычисляется как два радиуса. При заданной длине окружности можно определить ее диаметр путем деления длины на число «пи». К примеру, при длине 10 сантиметров диаметр будет составлять 10: 3,14 = 3,18 сантиметра.
При заданной площади круга, вычисление диаметра проводят путем извлечения квадратного корня из данного числа, затем деления полученного ответа на число «пи». К примеру, при площади круга 25 квадратных сантиметров, квадратный корень составит 5 сантиметров, а после деления этого числа на 3,14, получим 1,59 см. Это и есть диаметр данной в задаче окружности.
Справиться с такими несложными вычислениями может и рядовой ученик школы, и инженер конструкторского бюро.
Прямой линии, соединяющий две точки окружности (сферы, гиперсферы) и проходящий через её центр || его длина.
- ru (геометр.)
- Величина сферического треугольника «»Y»» равна величине противолежащего ему треугольника «»ABCʹ»», в котором сторона «»АВ»» общая с треугольником «»Р»», а третий угол «»Сʹ»» лежит при конечной точке диаметра
сферы, идущего от «»С»» через центр сферы. - На катете прямоугольного треугольнике как на диаметре
построена окружность.
любого круглого или кажущегося круглым тела, вместилища, пространства.
- Круглый бассейн имеет сажени три в диаметре
. - На спине у каждого был вшит чёрный круг, вершка два в диаметре
.
максимальное расстояние между двумя точками множества (см. w:Гипотеза Борсука
).
- ru (матем.)
- Всякое «»n»»-мерное выпуклое тело диаметра
«»d»» может быть разбито на «»n»» + 1 частей меньшего диаметра
.
в два раза больше радиуса
два радиуса
два радиуса на одной линии
двойной радиус окружности
делит круг на половинки
делит окружность пополам
линия, делящая круг пополам
м. греч. поперечник, говоря о круге или шаре. Истинный диаметр светила, астроном. поперечник планеты в линейной мере; видимый диаметр, поперечник в градусах и в долях его, служащий мерою угла, под которым планета видна. Диаметральный, поперечный; поперек супротивный: толщина веревок меряется по окру ясности, а толщина бревен и деревьев диаметрально, в отрубе, в поперечнике
мера круга
отрезок прямой, соединяющий две точки окружности, проходящий через центр
отрезок, соединяющий две точки окружности и проходящий через ее центр
поперечник круга
радиус плюс радиус
радиус, переходящий в радиус
радиус, умноженный на два
самая длинная хорда
толщина круглоты
у всех советских сигарет он был равен 7,62 мм
удвоенный радиус
хорда, проходящая через центр окружности
шапочный размер
радиус + радиус
(греч., от dia — чрез, поперек, и metreo — меряю). Прямая линия, проходящая через центр круга или шара и соединяющая две противоположные точки окружности.
греч., от dia, чрез, поперек, и metreo, меряю. Поперечник: прямая линия, проходящая чрез центр круга или шара и ограниченная их окружностью.
линия, проходящая чрез центр сомкнутой кривой и разделяющая ее пополам.
прямая, проходящая через центр круга; она делит пополам окружность и площадь круга; равна двум радиусам.
Толщина круглоты.
Два радиуса.
Отрезок прямой, соединяющий две точки окружности, проходящий через центр.
У всех советских сигарет он был равен 7,62 мм.
Сколько весит
Изучение размеров нашей планеты будет неполным без другого параметра – массы. Она составляет 6*1024 килограмма. Объём планеты – свыше 1,08 триллиона кубических километров. Таким образом, плотность планеты составляет около 5,5 грамма на кубический сантиметр.
Измерение окружности и диаметра Земли представляет собой несложную математическую задачу. В этом случае следует применять число π. Однако в силу сжатия планеты длина экваториальная окружность несколько больше, нежели полярная. И из-за этого экваториальный и полярный радиус Земли будет немного отличаться. Зная же показатели окружности, диаметра и радиуса нашей планеты, несложно будет вычислить и площадь ее поверхности.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
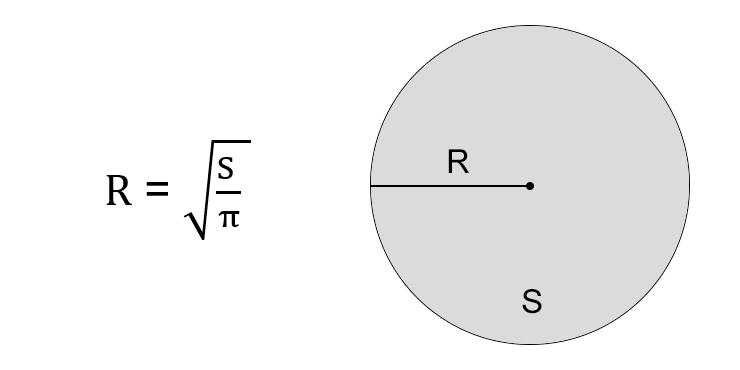 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
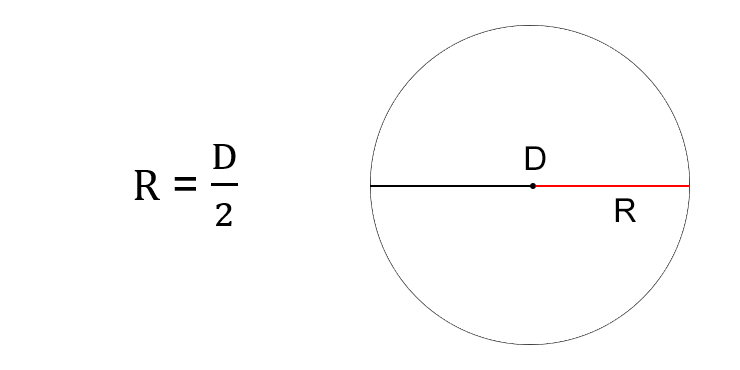 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
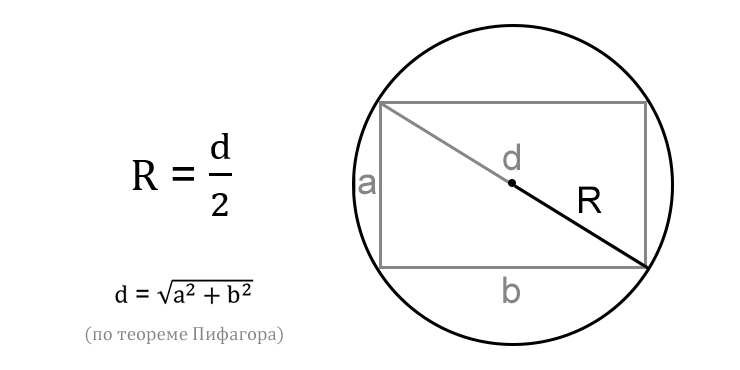 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
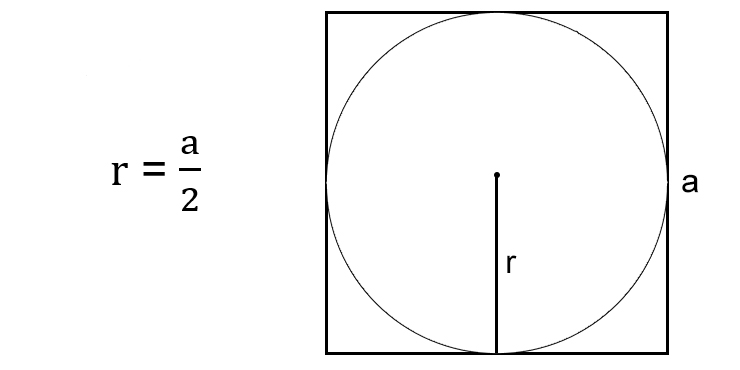 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
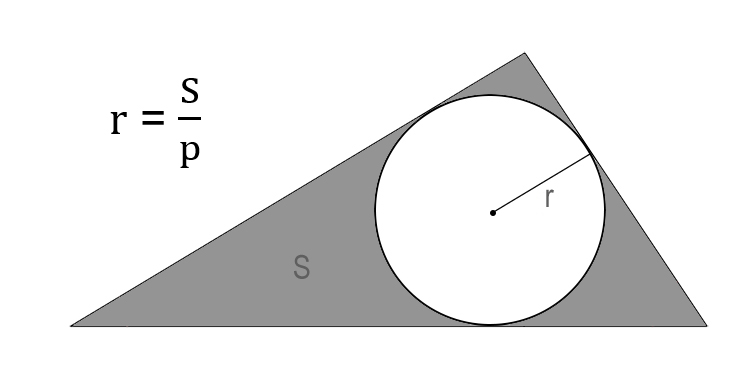 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.
- Найдите корень из полученного числа.
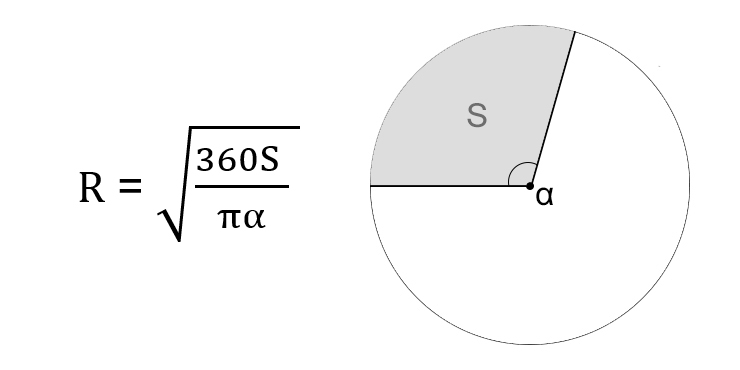 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
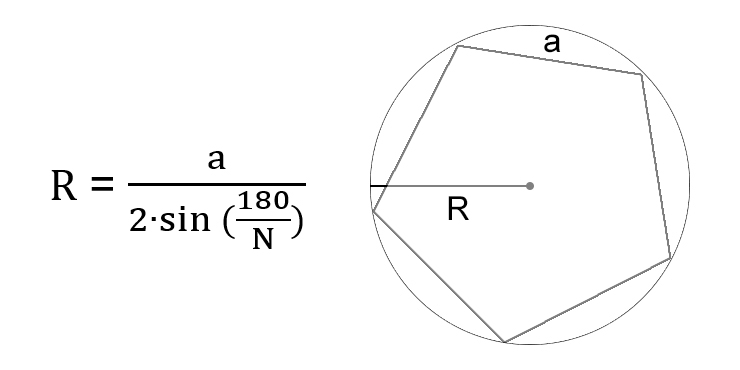 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Что такое радиус
И действительно:
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Обозначения и символ диаметра
Например, если речь идет о математике, то в ней чаще всего употребляется латинская буква «D». Причем допускается как прописное написание этой буквы, так и строчное – «d». Второй вариант даже чаще встречается в задачках.
Например, это может выглядеть так:
А вот если говорить о бытовом понятии «диаметра», то тут уже чаще используется другой символ. Это – перечеркнутая буква «О».
Именно такой знак вы наверняка увидите, когда речь идет о трубах, о размере сверла и так далее. И записываются они так:
По умолчанию считается, что подобные обозначения всегда считаются в миллиметрах.
Стоит сказать, что символа «Ø» нет на обычной раскладке клавиатуры. И чтобы напечатать его в тексте, нужно или открыть специальный раздел «дополнительные символы» в программе Word, или просто скопировать откуда-нибудь, а потом вставить.
Символ диаметра
Символы со сходным начертанием: Ø · ø · ∅
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как или ). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов» (ранее gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов (буква — латинская) или в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Сопряжённые диаметры эллипса
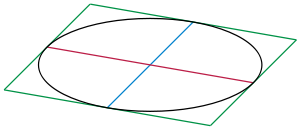
Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм
Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
На рисунке представлена пара сопряженных диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зеленые линии на рисунке).
- Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле r=abb2cos2φ+a2sin2φ=b1−e2cos2φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиус-вектором данной точки и осью абсцисс.
Сопряжённые диаметры гиперболы
Диаметры гиперболы
- Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
- Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением
-
k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}
-
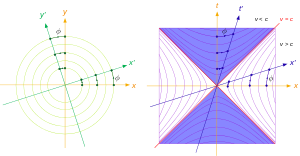
Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.
-
- Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
- Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
- В случае гипербол с асимптотами, образующими прямой угол, её сопряженные гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряженный диаметр, который будет просто диаметром сопряженной гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряженных диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряженных диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).
Вычисление диаметра окружности из чертежа окружности
- Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой.Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.
- Пометьте точки, в которых прямая пересекает окружность, буквами «A» и «B.»
- Начертите две пересекающиеся окружности, одну – с центром в точке A, а другую – с центром в точке B.Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.
- Через две точки, в которых окружности пересеклись, проведите прямую.Отрезок этой прямой между двумя точками и будет равен диаметру окружности.
- Измерьте диаметр.Измерьте его с помощью линейки, а если нужна большая точность – штангенциркулем с цифровой индикацией. Готово!
Интересное о земном экваторе
Территория, которая прилежит к экватору, имеет влажный и тёплый климат. Средняя температура на протяжении целого года колеблется от 25 до 30 градусов. Дождь идёт ежедневно. Экваториальные страны имеют такие интересные особенности.
- На экваторе расположено 14 стран. В его честь названо государство Эквадор.
- Экватор пересекает 33 острова, из которых 17 находится в Индонезии.
- Во всех экваториальных странах, кроме Габона и Сомали, установлены памятные знаки.
- На Галапагосском архипелаге находится вулкан Вольф. Его интересная особенность в том, что он расположен по обе стороны экватора.
- Недалеко от города Кито (столицы Эквадора) расположен вулкан Каямбе. Высота его около 4,7 км. Несмотря на то, что он находится на экваторе, его склоны покрыты снегом.
- Река Конго, которая находится в Африке, пересекает нулевую параллель два раза. Интересно, что на экваторе Земля вращается вокруг своей оси в 1,4 раза быстрее скорости звука. Поэтому здесь удобнее запускать космические спутники. При запуске экономится до 10 процентов ракетного топлива.