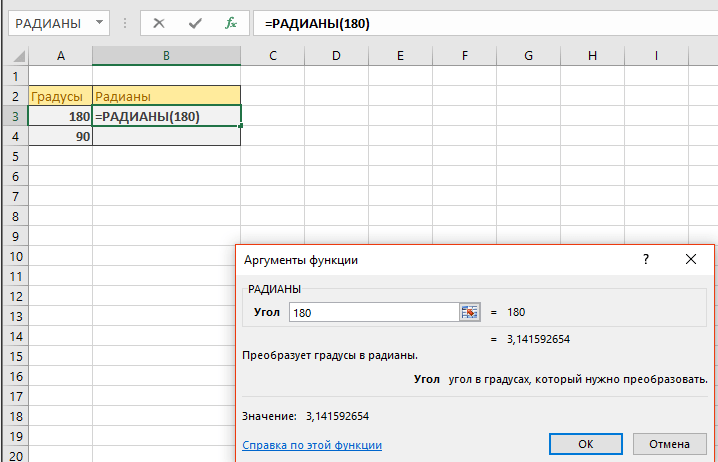
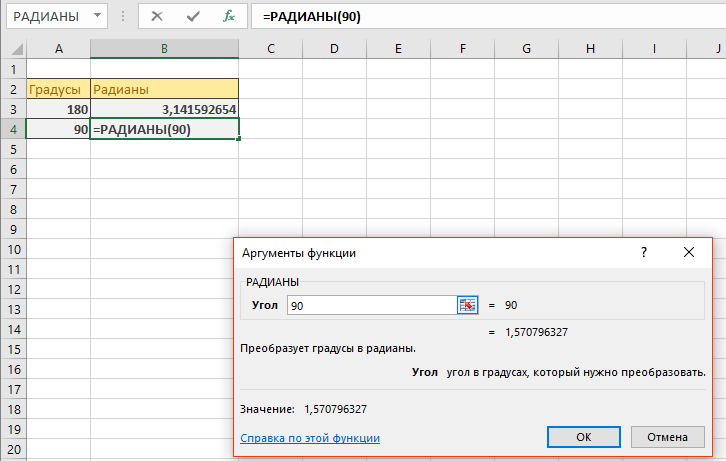
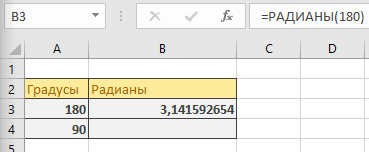
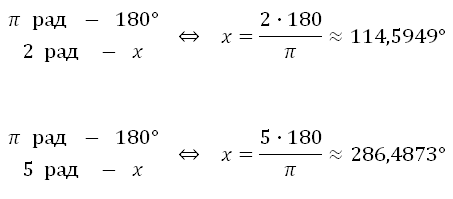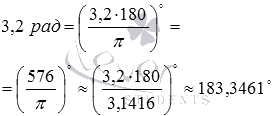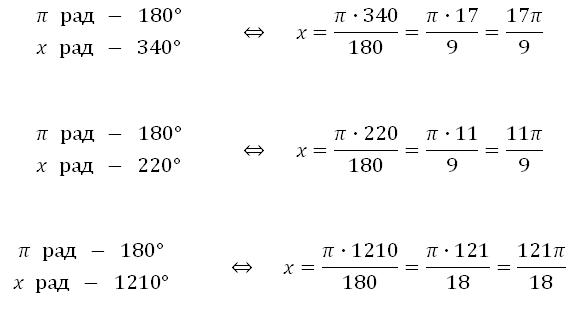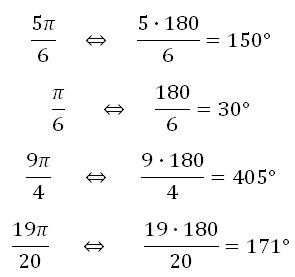Градусная мера угла. радианная мера угла. перевод градусов в радианы и обратно

Определение

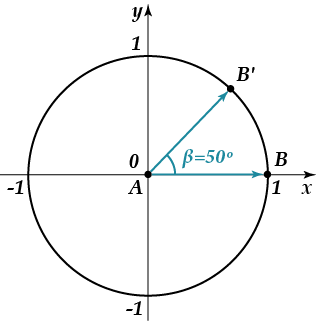
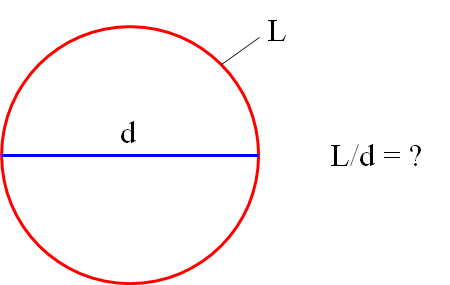
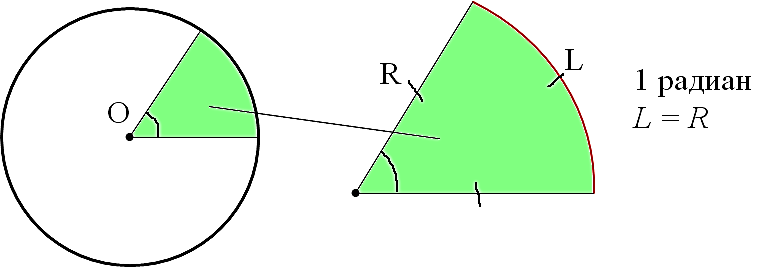
Радиан описывает плоскость угол которым видна круговой дуги , как длина дуги , деленному на радиус дуги. Один радиан угол , образуемый в центре круга с помощью дуги , которая равна по длине радиуса окружности. В более общем смысле величина такого вытянутого угла в радианах равна отношению длины дуги к радиусу круга; то есть θ = s / r , где θ — угол наклона в радианах, s — длина дуги, а r — радиус. И наоборот, длина замкнутой дуги равна радиусу, умноженному на величину угла в радианах; то есть s = rθ .

Хотя обычно утверждается, что как отношение двух длин радиан является « чистым числом », хотя Мор и Филлипс оспаривают это утверждение. Однако в математическом письме символ «рад» почти всегда опускается. При количественном определении угла в отсутствие какого-либо символа принимаются радианы, а когда подразумеваются градусы, используется символ ° . Радиан определяется как 1. Существуют разногласия относительно того, приемлемо ли в системе СИ считать углы безразмерными, поскольку они могут измеряться в градусах, радианах или циклах. Это может привести к путанице при рассмотрении единиц измерения частоты и постоянной Планка.

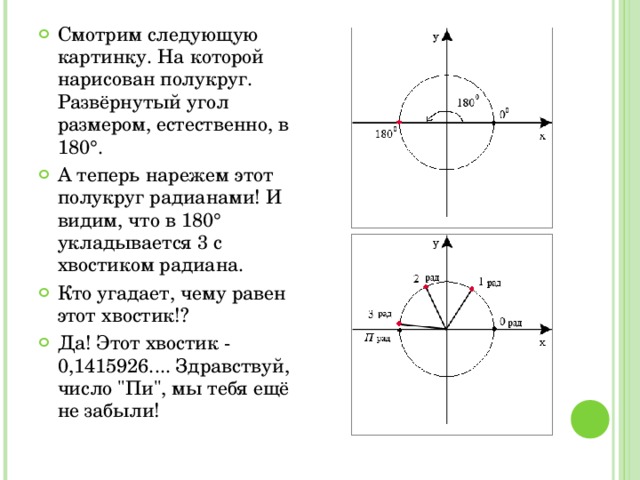
Полный оборот составляет 2 π радиан (здесь показан круг радиуса один и, следовательно, окружность 2 π ).

Отсюда следует, что величина в радианах одного полного оборота (360 градусов) равна длине всей окружности, деленной на радиус, или 2 π r / r , или 2 π . Таким образом, 2 π радиана равны 360 градусам, что означает, что один радиан равен 180 / π градусов.

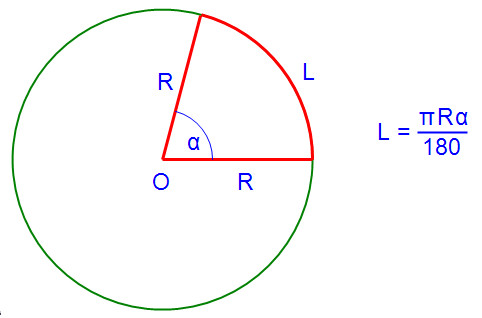
Соотношение 2 π рад = 360 ° может быть получено с использованием формулы для длины дуги . Взяв формулу для длины дуги, или . Предполагая единичный круг; радиус поэтому 1. Так как радиан является мерой угла , который стягивает дугу длиной , равной радиусу окружности, . Это можно еще упростить до . Умножение обеих сторон на 360 ° дает 360 ° = 2 π рад .
ℓарcзнак равно2πр(θ360∘){\ displaystyle \ ell _ {arc} = 2 \ pi r \ left ({\ tfrac {\ theta} {360 ^ {\ circ}}} \ right)}1знак равно2π(1 рад360∘){\ displaystyle 1 = 2 \ pi \ left ({\ tfrac {1 {\ text {rad}}} {360 ^ {\ circ}}} \ right)}1знак равно2π рад360∘{\ displaystyle 1 = {\ tfrac {2 \ pi {\ text {rad}}} {360 ^ {\ circ}}}}

[править] Размерность

Радиан есть безразмерной единицей измерения. То есть числовое значение угла, измеренного в радианах, лишено размерности. Это легко видеть из самого определения радиана, как отношения длины окружности к радиусу. Согласно рекомендациям Международного бюро мер и весов радиан интерпретируется как единица с размерностью 1 = м·м−1 (м/м, то есть метр на метр — числитель и знаменатель возможно сократить, то есть оно не имеет размерности).

Иначе, безразмерность радиана можно видеть по выражению ряда Тейлора для тригонометрической функции sin(x):

\sin(x) = x — \frac{x^3}{3!} + \frac{x^5}{5!}-\cdots.

Если бы x имел размерность, тогда эта сумма была бы лишена смысла — линейное слагаемое x нельзя было бы добавить к кубическому x3/3!, как величины разных размерностей. Итак, x должен быть безразмерным.

Сеть магазинов единиц радиана

Метрические префиксы ограничили использование с радианами и ни одним в математике.

milliradian (mrad) является одной тысячной радиана, и микрорадиан (urad или μrad) является одной миллионной радиана, т.е. 10 мрад = 10 urad = 1 радиус

Есть 2π × 1000 milliradians (≈ 6 283,185 мрад) в кругу. Таким образом, тригонометрический milliradian находится только под круга. Эта «реальная» тригонометрическая единица углового измерения круга используется изготовителями оптического прицела, использующими (stadiametric) rangefinding в сетках.

Расхождение лазерных лучей также обычно измеряется в milliradians.

Приближение тригонометрического milliradian (0,001 радиуса), известный как (угловой) mil, используется НАТО и другими военными организациями в артиллерийском деле и планировании. Каждый угловой mil представляет круга и на 1-⅞ % меньше, чем тригонометрический milliradian. Для маленьких углов, как правило, найденных в планировании для работы, удобство использования номера 6400 в вычислении перевешивает маленькие математические ошибки, которые это вводит. В прошлом другие системы артиллерийского дела привыкли различные приближения для; например, Швеция использовала streck и используемый СССР.

Будучи основанным на milliradian, НАТО mil подухаживает примерно за 1 м в диапазоне 1 000 м (под такими маленькими углами, искривление незначительно).

Меньшие единицы как микрорадианы (μrad) и nanoradians (nrad) используются в астрономии и могут также использоваться, чтобы измерить качество луча лазеров с ультранизким расхождением. Более распространенный вторая дуга, который является радианами (приблизительно 4,8481 микрорадиана). Точно так же префиксы, меньшие, чем milli-, потенциально полезны в измерении чрезвычайно маленьких углов.

[править] См. также


Основные единицы	Ампер · Кандела · Кельвин · Килограмм · Метр · Моль · Секунда
Производные единицы	Беккерель · Ватт · Вебер · Вольт · Генри · Герц · Градус Цельсия · Грей · Джоуль · Зиверт · Катал · Кулон · Люкс · Люмен · Ньютон · Ньютон-метр · Ом · Паскаль · Радиан · Сименс · Стерадиан · Тесла · Фарад
Принятые для использования с СИ	Ангстрем · Астрономическая единица · Гектар · Градус дуги (Минута дуги, Секунда дуги) · Дальтон (Атомная единица массы) · Децибел · Литр, Кубический километр · Микрограмм (Миллиграмм) · Микросекунда (Миллисекунда, Наносекунда) · Микрометр (Нанометр, Сантиметр, Фемтометр, Километр) · Непер · Сутки (Час, Минута) · Тонна · ЭлектронвольтАтомная система единиц · Естественная система единиц
См. также	История метрической системы · Квантовая система единиц · Новые определения СИ · Планковская длина · Преобразование единиц · Приставки СИ · Система физических величин

[править] Свойства

Широкое применение радианов в математическом анализе обусловлено тем, что выражения с тригонометрическими функциями, аргументы которых измеряются в радианах, приобретают максимально простой вид (без числовых коэффициентов). Например, используя радианы, получим простое тождество

\lim_{h\rightarrow 0}\frac{\sin h}{h}=1,

что лежит в основе многих элегантных формул в математике.

При малых углах синус и тангенс угла, выраженного в радианах, равен самому углу, что удобно при приближенных вычислениях.

Косинус малого угла, выраженного в радианах, приблизительно равен:

\cos(x) \approx 1 — \frac{x^2}{2}

Комментарий эксперта

Чисто мануальная чистка лица не оправдана. Механическим путем можно очистить отдельные элементы сыпи, но полностью очищать кожу только мануальным способом травматично. Лучше всего комбинировать способы очищения.

Конверсии

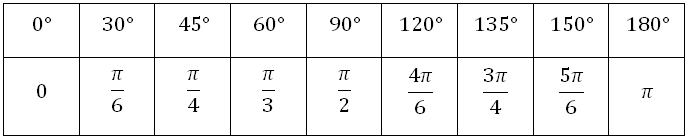
Таблица для преобразования между градусами и радианами

Преобразование общих углов
Повороты	Радианы	Градусы	Градианы или угоны
0 °	0 г
124	π12	15 °	16 +23грамм
112	π6	30 °	33 +13грамм
110	π5	36 °	40 г
18	π4	45 °	50 г
12 π	1	c. 57,3 °	c. 63,7 г
16	π3	60 °	66 +23грамм
15	2 π5	72 °	80 г
14	π2	90 °	100 г
13	2 π3	120 °	133 +13грамм
25	4 π5	144 °	160 г
12	π	180 °	200 г
34	3 π2	270 °	300 г
1	2 π	360 °	400 г

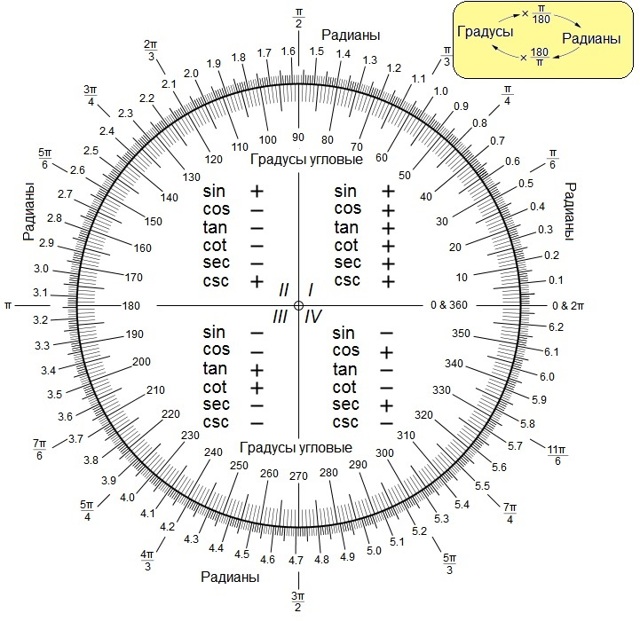
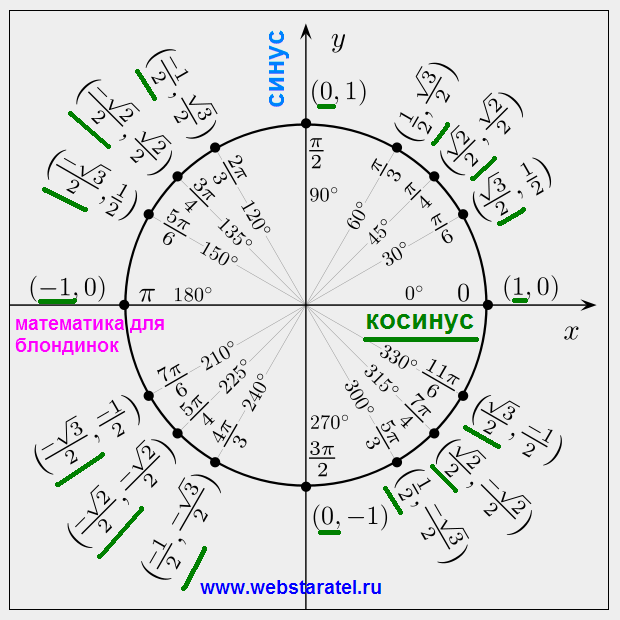
Преобразование радианов в градусы

Как указано, один радиан равен 180 / π градусов. Таким образом, чтобы преобразовать радианы в градусы, умножьте на 180 / π .

угол в градусахзнак равноугол в радианах⋅180∘π{\ displaystyle {\ text {угол в градусах}} = {\ text {угол в радианах}} \ cdot {\ frac {180 ^ {\ circ}} {\ pi}}}

Например:

1 радзнак равно1⋅180∘π≈57,2958∘{\ displaystyle 1 {\ text {rad}} = 1 \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} \ приблизительно 57,2958 ^ {\ circ}}

2,5 радзнак равно2,5⋅180∘π≈143,2394∘{\ displaystyle 2.5 {\ text {rad}} = 2.5 \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} \ приблизительно 143,2394 ^ {\ circ}}

π3 радзнак равноπ3⋅180∘πзнак равно60∘{\ displaystyle {\ frac {\ pi} {3}} {\ text {rad}} = {\ frac {\ pi} {3}} \ cdot {\ frac {180 ^ {\ circ}} {\ pi} } = 60 ^ {\ circ}}

И наоборот, чтобы преобразовать градусы в радианы, умножьте на π / 180.

угол в радианахзнак равноугол в градусах⋅π180∘{\ displaystyle {\ text {угол в радианах}} = {\ text {угол в градусах}} \ cdot {\ frac {\ pi} {180 ^ {\ circ}}}}

Например:

1∘знак равно1⋅π180∘≈0,0175 рад{\ displaystyle 1 ^ {\ circ} = 1 \ cdot {\ frac {\ pi} {180 ^ {\ circ}}} \ приблизительно 0,0175 {\ text {rad}}}

23∘знак равно23⋅π180∘≈0,4014 рад{\ displaystyle 23 ^ {\ circ} = 23 \ cdot {\ frac {\ pi} {180 ^ {\ circ}}} \ приблизительно 0,4014 {\ text {rad}}}

Радианы можно преобразовать в обороты (полные обороты), разделив количество радианов на 2 π .

Перевод радиана в градус

Длина окружности окружности равна , где — радиус окружности.
2πр{\ displaystyle 2 \ pi r}р{\ displaystyle r}

Таким образом, верно следующее эквивалентное соотношение:

360∘⟺2πр{\ displaystyle 360 ^ {\ circ} \ iff 2 \ pi r}
360∘{\ displaystyle 360 ^ {\ circ}}

По определению радиана полный круг представляет:

2πрр рад{\ displaystyle {\ frac {2 \ pi r} {r}} {\ text {rad}}}

знак равно2π рад{\ displaystyle = 2 \ pi {\ text {rad}}}

Объединяя оба вышеуказанных отношения:

2π радзнак равно360∘{\ displaystyle 2 \ pi {\ text {rad}} = 360 ^ {\ circ}}

⇛1 радзнак равно360∘2π{\ displaystyle \ Rrightarrow 1 {\ text {rad}} = {\ frac {360 ^ {\ circ}} {2 \ pi}}}

⇛1 радзнак равно180∘π{\ displaystyle \ Rrightarrow 1 {\ text {rad}} = {\ frac {180 ^ {\ circ}} {\ pi}}}

Преобразование радианов в градусы

2π{\ displaystyle 2 \ pi}радиан равен одному поворот , который , по определению , 400 gradians (400 Гоны или 400 г ). Итак, чтобы преобразовать радианы в градусы, умножьте на , а для преобразования из градианов в радианы умножьте на . Например,
200π{\ displaystyle 200 / \ pi}π200{\ displaystyle \ pi / 200}

1.2 радзнак равно1.2⋅200граммπ≈76,3944грамм{\ displaystyle 1.2 {\ text {rad}} = 1.2 \ cdot {\ frac {200 ^ {\ text {g}}} {\ pi}} \ приблизительно 76,3944 ^ {\ text {g}}}

50граммзнак равно50⋅π200грамм≈0,7854 рад{\ displaystyle 50 ^ {\ text {g}} = 50 \ cdot {\ frac {\ pi} {200 ^ {\ text {g}}}} \ приблизительно 0,7854 {\ text {rad}}}

Кратные SI

Метрические префиксы имеют ограниченное использование с радианами и не используются в математике. Мрад (мрад) является тысячной радиан и microradian (мкрад) представляет собой миллионный радиан, т.е. 1 рад = 10 3 мрад = 10 6 мкрада .

В круге 2 π × 1000 миллирадиан (≈ 6283,185 мрад). Так что миллирадиан чуть меньше16283угла, образуемого полным кругом. Эта «настоящая» единица углового измерения круга используется производителями оптических прицелов, использующими (стадиометрический) дальномер в сетках . Дивергенции от лазерных лучей также обычно измеряется в миллирадианах.

Приближенное значение миллирадиана (0,001 рад) используется НАТО и другими военными организациями при стрельбе и . Каждый угловой мил представляет16400 круга и является 158% или на 1,875% меньше миллирадиана. Для малых углов, которые обычно встречаются при наведении на цель, удобство использования числа 6400 в расчетах перевешивает небольшие математические ошибки, которые оно вносит. В прошлом другие артиллерийские системы использовали разные приближения к12000 π; например Швеция использовала16300 Streck и СССР использовали16000. Основываясь на миллирадианах, мила НАТО выступает примерно на 1 м на дальности 1000 м (при таких малых углах кривизна незначительна).

Меньшие единицы, такие как микрорадианы (мкрад) и нанорадианы (нрад), используются в астрономии, а также могут использоваться для измерения качества луча лазеров со сверхмалой расходимостью. Чаще всего используется угловая секунда , т.е.π648 000 рад (около 4,8481 микрорадиан). Точно так же префиксы меньше милли- потенциально полезны при измерении очень малых углов.

Использование в физике

Радиан широко используется в физике, когда требуются угловые измерения. Например, угловая скорость обычно измеряется в радианах в секунду (рад / с). Один оборот в секунду равен 2 π радиан в секунду.

Точно так же угловое ускорение часто измеряется в радианах в секунду в секунду (рад / с 2 ).

В целях анализа размеров единицами измерения угловой скорости и углового ускорения являются с -1 и с -2 соответственно.

Точно так же разность фаз двух волн также может быть измерена в радианах. Например, если разность фаз двух волн составляет ( k ⋅2 π ) радиан, где k — целое число, они считаются синфазными , а если разность фаз двух волн равна ( k ⋅2 π + π ), где k — целое число, они считаются противофазными.

Используйте в физике

Радиан широко используется в физике, когда угловые измерения требуются. Например, угловая скорость, как правило, измеряется в радианах в секунду (rad/s). Одна революция в секунду равна 2π радианы в секунду.

Точно так же угловое ускорение часто измеряется в радианах в секунду в секунду (rad/s).

В целях размерного анализа единицы — s и s соответственно.

Аналогично, разность фаз двух волн может также быть измерена в радианах. Например, если разность фаз двух волн (k · 2π) радианы, где k — целое число, их рассматривают в фазе, пока, если разность фаз двух волн (k · 2π + π), где k — целое число, их рассматривают в антифазе.

Радиан в Международной системе единиц (СИ)

В качестве единицы измерения плоских углов в Международной системе единиц (СИ) радиан был принят XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием системы СИ в целом. В настоящее время в системе СИ радиан квалифицируется как когерентная безразмерная производная единица СИ, имеющая специальные наименование и обозначение. Русское обозначение — рад, международное — rad.

Безразмерность плоского угла означает, что единицей его измерения является число один. Однако, применительно к плоскому углу единице «один» было присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно величина имеется в виду.

Кратные и дольные единицы

Десятичные кратные и дольные единицы радиана образуются с помощью стандартных приставок СИ, однако используются редко. Так, в миллирадианах, микрорадианах и нанорадианах измеряется угловое разрешение в астрономии. В кратных единицах (килорадианах и т. д.) измеряется
набег угловой фазы. Сокращённое обозначение (рад, rad) основной и производных единиц не следует путать с устаревшей единицей измерения поглощённой дозы ионизирующего излучения — рад.

Кратные	Дольные
величина	название	обозначение	величина	название	обозначение
101 рад	декарадиан	дарад	darad	10−1 рад	децирадиан	драд	drad
102 рад	гекторадиан	град	hrad	10−2 рад	сантирадиан	срад	crad
103 рад	килорадиан	крад	krad	10−3 рад	миллирадиан	мрад	mrad
106 рад	мегарадиан	Мрад	Mrad	10−6 рад	микрорадиан	мкрад	µrad
109 рад	гигарадиан	Град	Grad	10−9 рад	нанорадиан	нрад	nrad
1012 рад	терарадиан	Трад	Trad	10−12 рад	пикорадиан	прад	prad
1015 рад	петарадиан	Прад	Prad	10−15 рад	фемторадиан	фрад	frad
1018 рад	эксарадиан	Эрад	Erad	10−18 рад	атторадиан	арад	arad
1021 рад	зеттарадиан	Зрад	Zrad	10−21 рад	зепторадиан	зрад	zrad
1024 рад	иоттарадиан	Ирад	Yrad	10−24 рад	иокторадиан	ирад	yrad
применять не применяются или редко применяются на практике

Связь радиана с другими единицами

Угол в 1 радиан.

Пропорциональное соотношение радиана с другими единицами измерения углов описывается формулой:

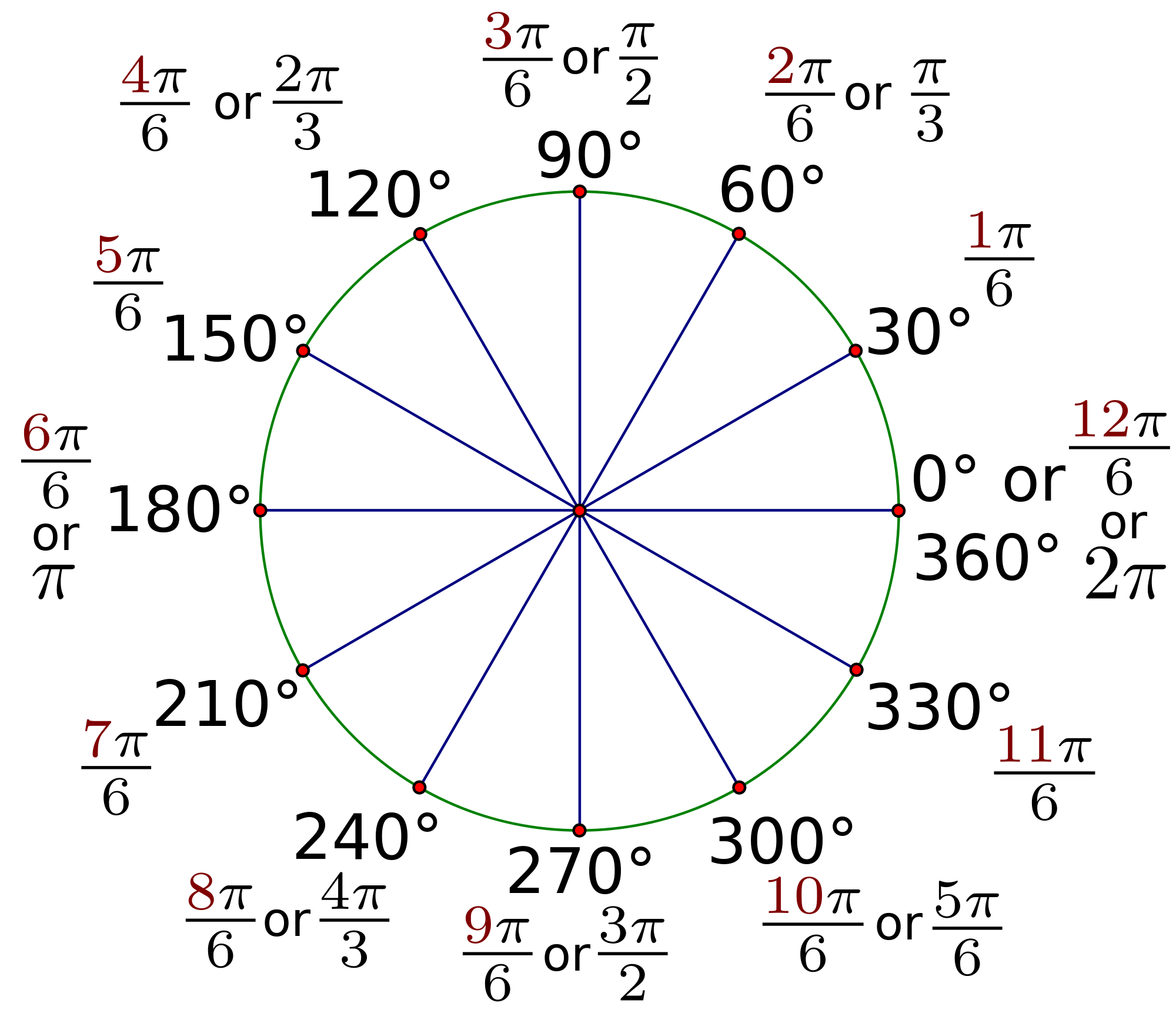
1 радиан = 1/(2π) оборотов = 180/π градусов = 200/π градов.

Очевидно, развернутый угол равен 180∘,{\displaystyle 180^{\circ },} или π⋅rr=π{\displaystyle {\frac {\pi \cdot r}{r}}=\pi } радианам. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.

a = α × (360° / (2π)) или α × (180° / π),

α = a : (180° / π) = a × (π / 180°),

где α — угол в радианах, a — угол в градусах.

p′{\displaystyle p’} (или 1 рад в минутах) = 360∘⋅60′2π≈3437,747′{\displaystyle {\frac {360^{\circ }\cdot 60′}{2\pi }}\approx 3437{,}747′}

p″{\displaystyle p»} (или 1 рад в секундах) = 360∘⋅60′⋅60″2π≈206264,8″.{\displaystyle {\frac {360^{\circ }\cdot 60’\cdot 60»}{2\pi }}\approx 206264{,}8».}

Номограмма для перевода радианы/градусы.

В метрической системе угловых мер прямой угол делится на 100 градов и каждый град на 100 сантиградов, который, в свою очередь, делится на сотые доли сантиграда, так чтоp‵‵{\displaystyle p^{\backprime \backprime }} (или 1 рад в сотых долях «сантиграда») = 400⋅100⋅1002π=636620.{\displaystyle {\frac {400\cdot 100\cdot 100}{2\pi }}=636620.} Употреблять его практически не приходится, так как метрическая система угловых мер пока не получила широкого распространения.

Чтобы легче запомнить, как переводят радианы в градусы и обратно, заметим:
Переводя радианы в градусы (или в минуты, или в секунды), мы из отвлеченного числа (rad{\displaystyle \mathrm {rad} }) делаем именованное (p∘,p′,p″{\displaystyle p^{\circ },p’,p»}) и поэтому должны множить на p∘ ({\displaystyle p^{\circ }~(}или p′,p″){\displaystyle p’,p»)};
Переводя градусы в радианы, мы, наоборот, уничтожаем наименование: получаем отвлечённое число; значит, здесь надо делить на p∘ ({\displaystyle p^{\circ }~(}или p′,p″),{\displaystyle p’,p»),} либо же умножать на перевёрнутую
дробь 1p∘ (1p′,1p″).{\displaystyle {\frac {1}{p^{\circ }}}~({\frac {1}{p’}},{\frac {1}{p»}}).}

Пример 1. Перевести в радианы 5∘43′46″.{\displaystyle 5^{\circ }43’46».}

αrad≖5∘=5∘p∘ rad=0,08726{\displaystyle {\boldsymbol {\alpha }}\eqcirc 5^{\circ }={\frac {5^{\circ }}{\displaystyle {p^{\circ }}}}~\mathrm {rad} =0{,}0872_{6}}

43′=43′p′ rad=0,012508{\displaystyle 43’={\frac {43′}{p’}}~\mathrm {rad} =0{,}0125_{08}}

46″=46″p″ rad=0,000223{\displaystyle 46»={\frac {46»}{p»}}~\mathrm {rad} =0{,}0002_{23}}

∑≈0,09999 rad{\displaystyle \sum \approx 0{,}0999_{9}~\mathrm {rad} }=,1 rad{\displaystyle =0{,}1~\mathrm {rad} }

Альтернативный способ предусматривает перевод минут и секунд в десятичные (сотые и десятитысячные) доли градуса, и однократного деления на p∘{\displaystyle p^{\circ }:} (как правило, этот способ более точен)

46″=46″60″=,77′{\displaystyle 46»={\frac {46»}{60»}}=0{,}{\boldsymbol {77}}’}

43,77′=43,77′60′=,7295∘{\displaystyle 43{,}{\boldsymbol {77}}’={\frac {43{,}77′}{60′}}=0{,}{\boldsymbol {7295}}^{\circ }}

∑=5,7295∘{\displaystyle \sum =5{,}{\boldsymbol {7295}}^{\circ }}

5,7295∘=5,7295∘p∘ rad=5,7295∘57,295∘=,1 rad{\displaystyle 5{,}7295^{\circ }={\frac {5{,}7295^{\circ }}{p^{\circ }}}~\mathrm {rad} ={\frac {5{,}7295^{\circ }}{\displaystyle {57{,}295^{\circ }}}}=0{,}1~\mathrm {rad} }

Пример 2. Перевести в градусы 1 радиан.

a∘≖1⋅360∘2π=1⋅57,29578∘=57,29578∘{\displaystyle a\eqcirc 1\cdot {\frac {360^{\circ }}{2\pi }}=1\cdot 57{,}29578^{\circ }=57{,}{\boldsymbol {29578}}^{\circ }}

,29578∘⋅60′=17,7468′{\displaystyle 0{,}{\boldsymbol {29578}}^{\circ }\cdot 60’=17{,}{\boldsymbol {7468}}’}

,7468′⋅60″=44,807″≈45″{\displaystyle 0{,}{\boldsymbol {7468}}’\cdot 60»=44{,}807»\approx 45»}

Итого ≈57∘17′45″.{\displaystyle \approx 57^{\circ }17’45».}