Механическая работа. мощность

Что такое ПАТЭС

Если не усложнять, то плавучая атомная электростанция мало, чем отличается от той, что расположена на суше за исключением опоры, на которой она построена.

ПАТЭС состоит из плавучего энергоблока, береговой инфраструктуры для выдачи электрической и тепловой энергии потребителям, а так же гидротехнических сооружений, которые отвечают за безопасную стоянку в акватории.

Сам энергоблок имеет не меньше, а даже больше степеней защиты, так как потенциально на него может быть больше воздействий и инженеры постарались все предусмотреть. В первую очередь, это касается очень мощной плавучей основы. Все ее части двуслойные, то есть даже столкновение с чем-либо не должно сильно навредить ПАТЭС.

На Академике Ломонсове установлено два атомных реактора типа КЛТ-40С. Электрическая мощность каждого составляет 35 МВт. В сумме получается максимальная электрическая мощность всей станции на уровне 70 МВт. Этого достаточно для перекрытия потребностей в энергии населенного пункта, в котором проживает до 100 000 человек.

Кроме выработки электроэнергии, станция может вырабатывать и тепло. Максимальная тепловая мощность составляет 50 Гкал/ч. Но и этим не ограничивается применение ПАТЭС Академик Ломоносов.

Чтобы станция была еще больше похожа на швейцарский нож, ее оснастили системой опреснения воды, которая должна опреснять до 240 тысяч кубометров морской воды в сутки.

Академика Ломоносова начали строить еще в 2007 году и только сейчас он был введен в промышленную эксплуатацию. Хотя, первую энергию в сеть он начал передавать еще в декабре 2019 года.

Так объект выглядел на этапе строительства

Работа в термодинамике

В термодинамике работа, совершённая газом при расширении, рассчитывается как интеграл давления по объёму:

A1→2=∫V1V2PdV.{\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

dA=PdSh.{\displaystyle dA=PdSh.}

Видно, что это и есть произведение давления на приращение объёма вблизи данной элементарной площадкой. А просуммировав по всем dS, получим конечный результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

Чем занимаются физики

Физики и инженеры. Сразу оговорюсь, что в этой статье физик и инженер будут близки по смыслу. Но фактически вы должны разделять: ученые-физики — это по большей мере теоретики, а инженеры — это практики, которые разрабатывают устройства, поддерживают работу оборудования и пишут программы.

Где нужны физики. Смартфон — понятный и доступный всем гаджет. Инженеры разрабатывают это устройство с нуля: работу аккумулятора, новейшие дисплеи, процессоры, оптику в камерах, системы распознавания лиц и отпечатков пальцев, стандарты сотовой связи. Всё это — физика. Уже после разработки этих компонентов в дело вступают программисты. Они пишут операционные системы и приложения.

Разработчики с физическим образованием занимаются наноматериалами, телевизорами на квантовых точках, строят АЭС и придумывают конструкции новых электрокаров. Перечислять можно очень долго. Как-то мой преподаватель сказал: «Физика — это всё, что мы видим вокруг себя», — эта фраза лучше всего описывает широту применения профессии.

Работа силы в теоретической механике

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка M{\displaystyle M} движется по непрерывно дифференцируемой кривой G={r=r(s)}{\displaystyle G=\{r=r(s)\}}, где s — переменная длина дуги, ≤s≤S{\displaystyle 0\leq s\leq S}, и на неё действует сила F(s){\displaystyle F(s)}, направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под F(s){\displaystyle F(s)} проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).
Величина F(ξi)△si,△si=si−si−1,i=1,2,…,iτ{\displaystyle F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,…,i_{\tau }}, называется элементарной работой силы F{\displaystyle F} на участке Gi{\displaystyle G_{i}} и принимается за приближённое значение работы, которую производит сила F{\displaystyle F}, воздействующая на материальную точку, когда последняя проходит кривую Gi{\displaystyle G_{i}}. Сумма всех элементарных работ ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} является интегральной суммой Римана функции F(s){\displaystyle F(s)}.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма ∑i=1iτF(ξi)△si{\displaystyle \sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}} всех элементарных работ, когда мелкость |τ|{\displaystyle |\tau |} разбиения τ{\displaystyle \tau } стремится к нулю, называется работой силы F{\displaystyle F} вдоль кривой G{\displaystyle G}.

Таким образом, если обозначить эту работу буквой W{\displaystyle W}, то, в силу данного определения,

W=lim|τ|→∑i=1iτF(ξi)△si{\displaystyle W=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}},

следовательно,

W=∫sF(s)ds{\displaystyle W=\int \limits _{0}^{s}F(s)ds} (1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра t{\displaystyle t} (например, времени) и если величина пройденного пути s=s(t){\displaystyle s=s(t)}, a≤t≤b{\displaystyle a\leq t\leq b} является непрерывно дифференцируемой функцией, то из формулы (1) получим

W=∫abFs(t)s′(t)dt.{\displaystyle W=\int \limits _{a}^{b}Fs'(t)dt.}

От чего зависит величина КПД

Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.

А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.

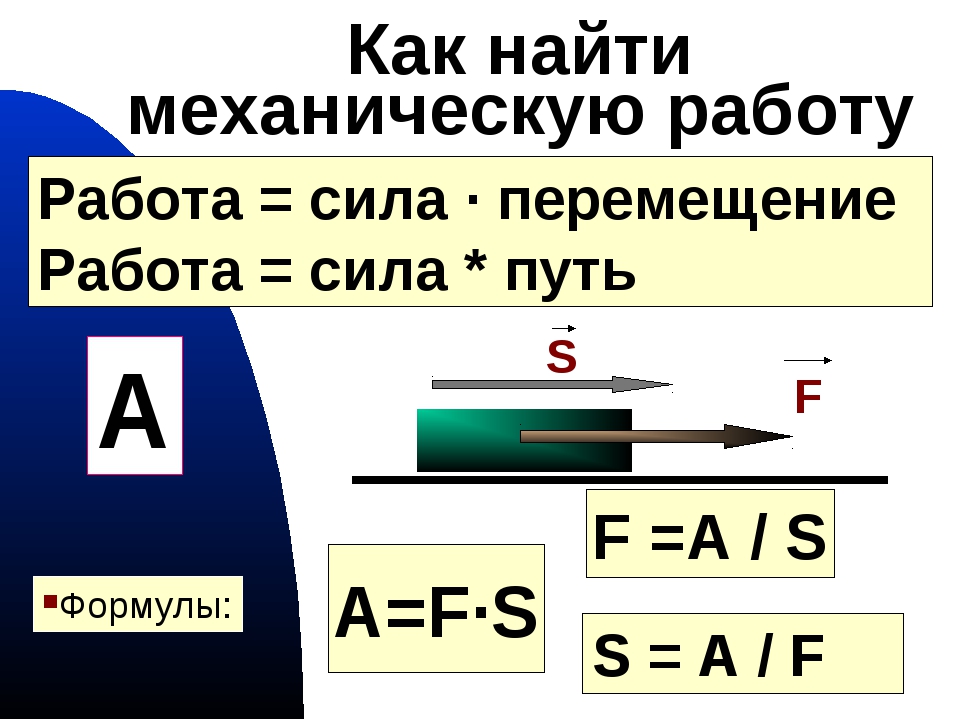
Формула работы

Теперь покажем, как количественно можно вычислить изучаемую величину. Перевод энергии между разными состояниями возможен только в том случае, если присутствует некоторая сила. Это может быть физическое усилие человеческих рук и ног, сила машин, создаваемое давление, которое легко пересчитывается в силу, в случае сгорания топлива в цилиндре, сила электромагнитной индукции электродвигателя и так далее.

На вопрос, как находить работу в физике, ответит следующая формула:

Работа A — это скалярная величина, в свою очередь сила F¯ и перемещение l¯ — это величины векторные. Именно поэтому в формуле для вычисления A используются круглые скобки, чтобы показать, что речь идет о скалярном произведении векторов. В скалярной форме выражение выше можно переписать в следующем виде:

Здесь φ является углом между векторами силы F¯ и перемещения l¯.

Поскольку перемещение измеряется в метрах, а сила в ньютонах, то единицей работы будет ньютон на метр (Н * м). В СИ эта единица имеется собственное название — джоуль (Дж). Получается, что работа в 1 Дж соответствует силе в 1 Н, которая, действуя вдоль направления смещения, переместила тело на 1 метр.

«Механическая работа. Механическая мощность»

Код ОГЭ 1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность.

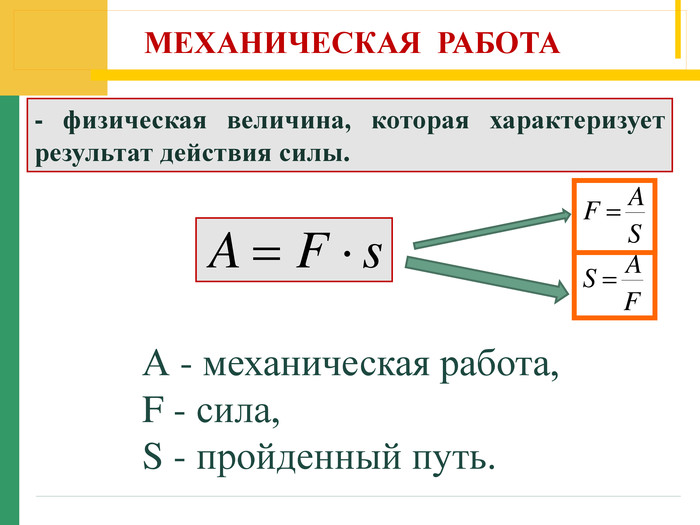
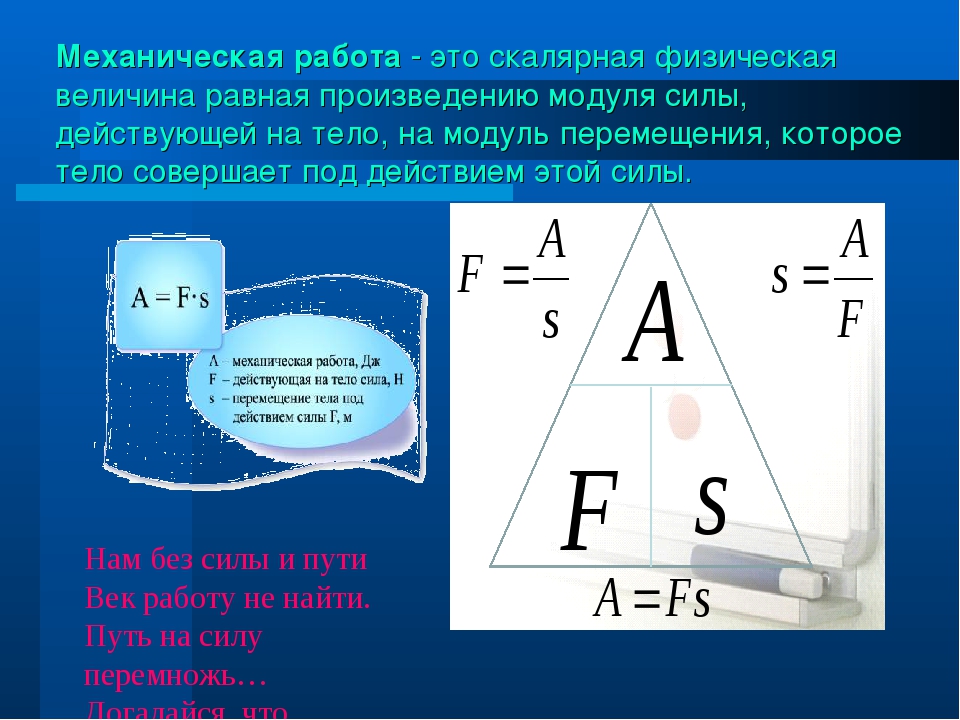
Работа силы – физическая величина, характеризующая результат действия силы.

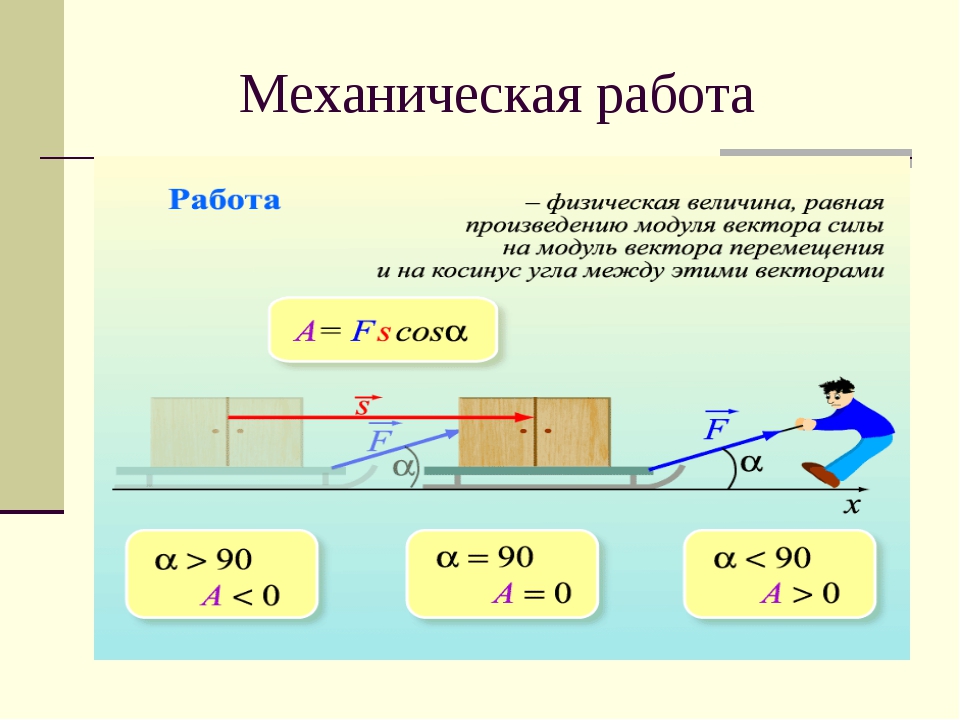
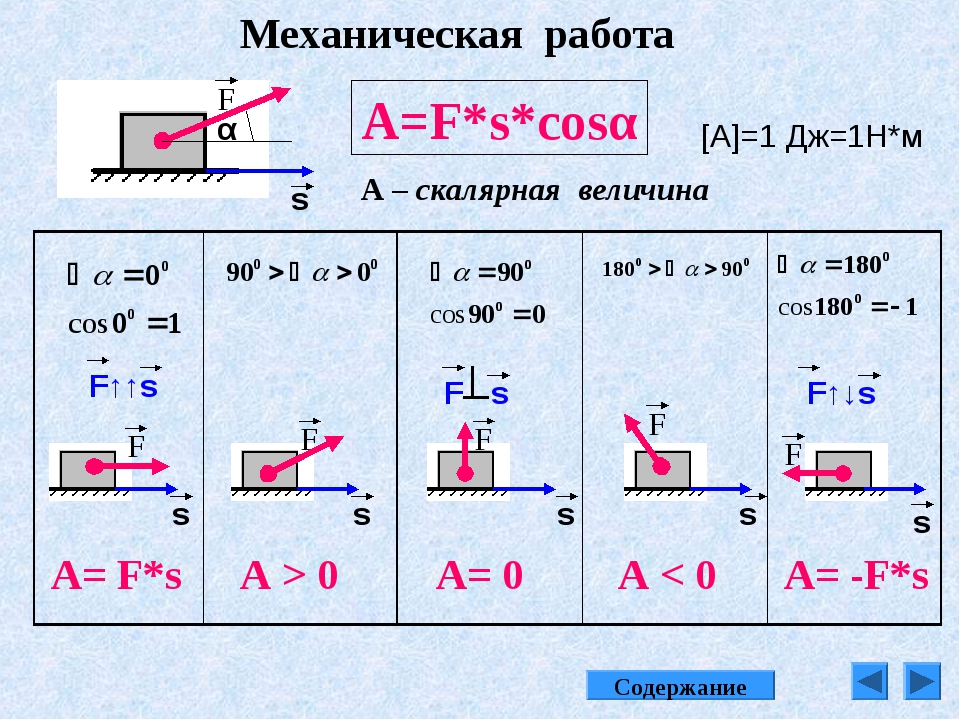
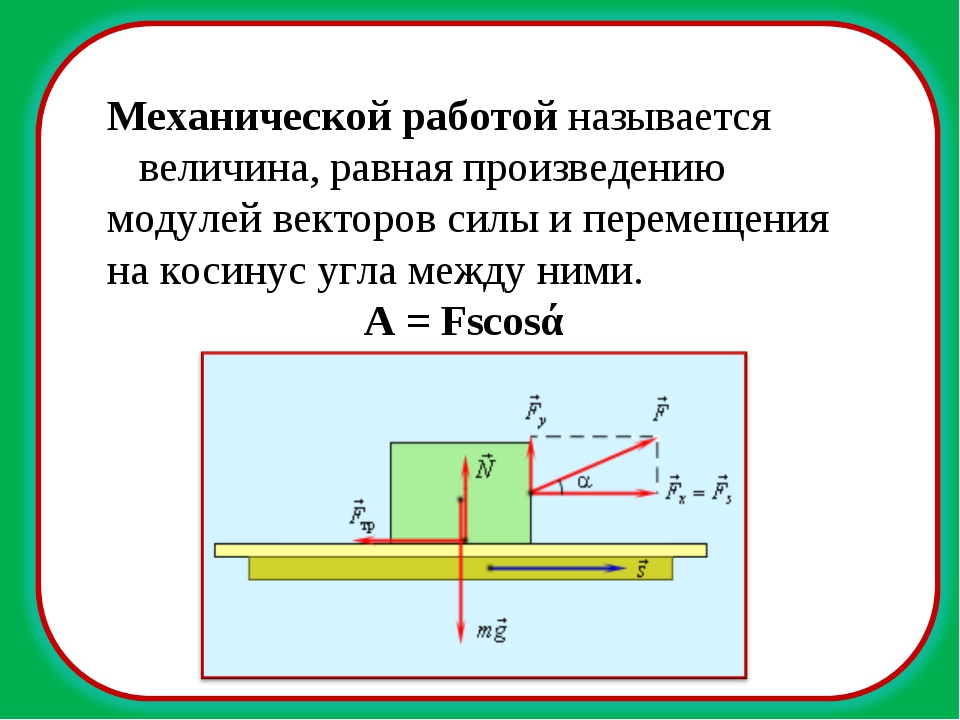
Механическая работа А постоянной силы равна произведению модуля вектора силы на модуль вектора перемещения и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а.

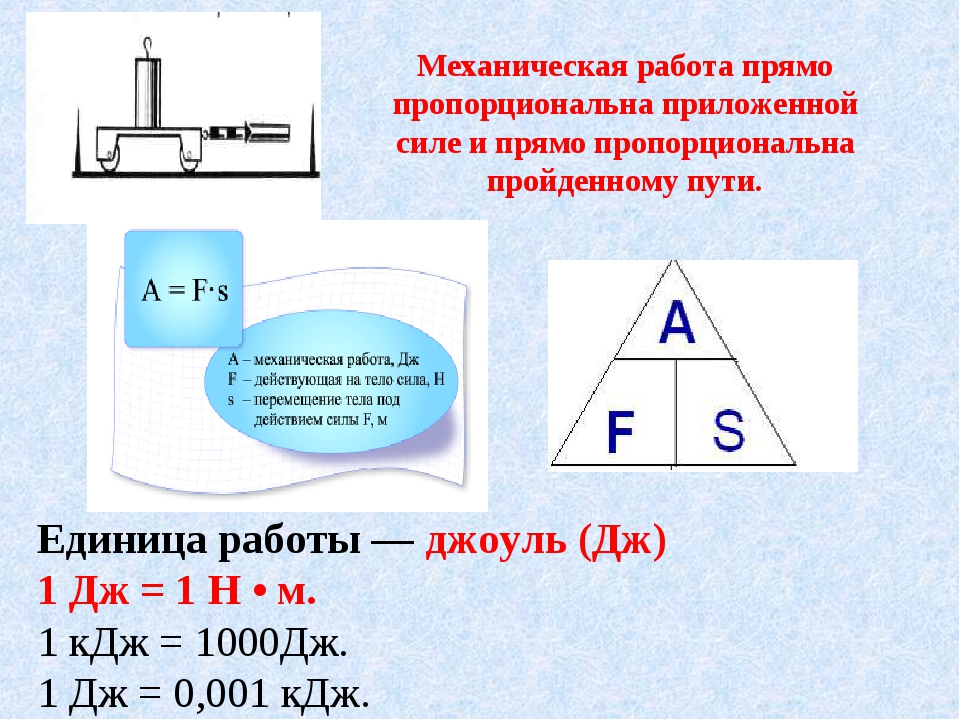
Единица измерения работы в СИ – джоуль: = Дж = Н • м.
Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.

Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:

сила действует, а тело не перемещается;
тело перемещается, а сила равна нулю;
угол между векторами силы и перемещения равен 90° (cos a = 0).

Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости. Работа – скалярная величина, она может быть как положительной, так и отрицательной

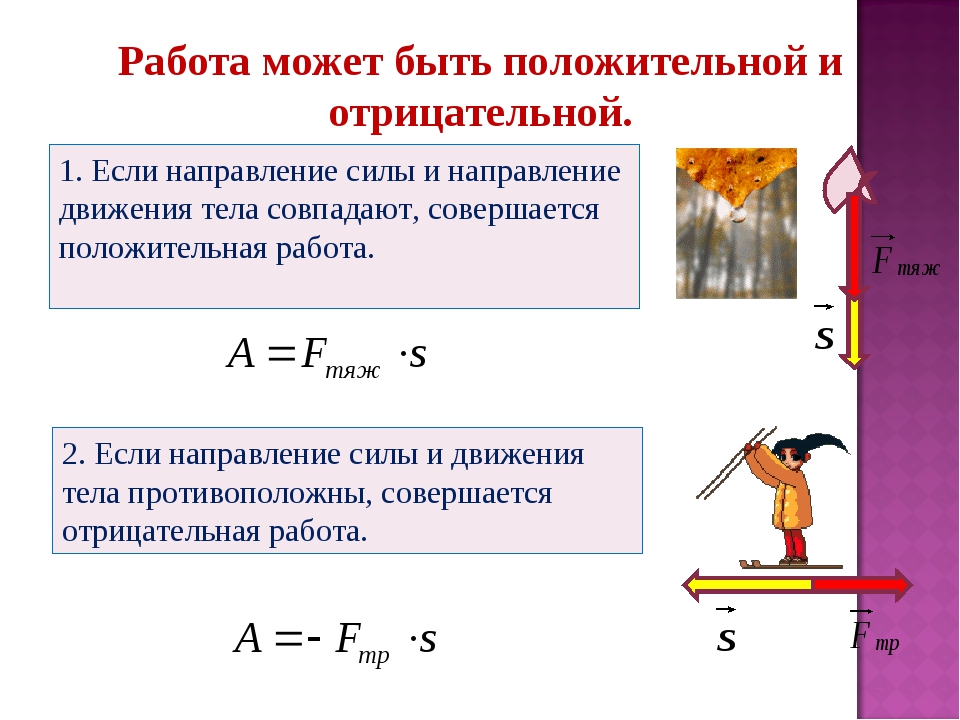
Работа – скалярная величина, она может быть как положительной, так и отрицательной.

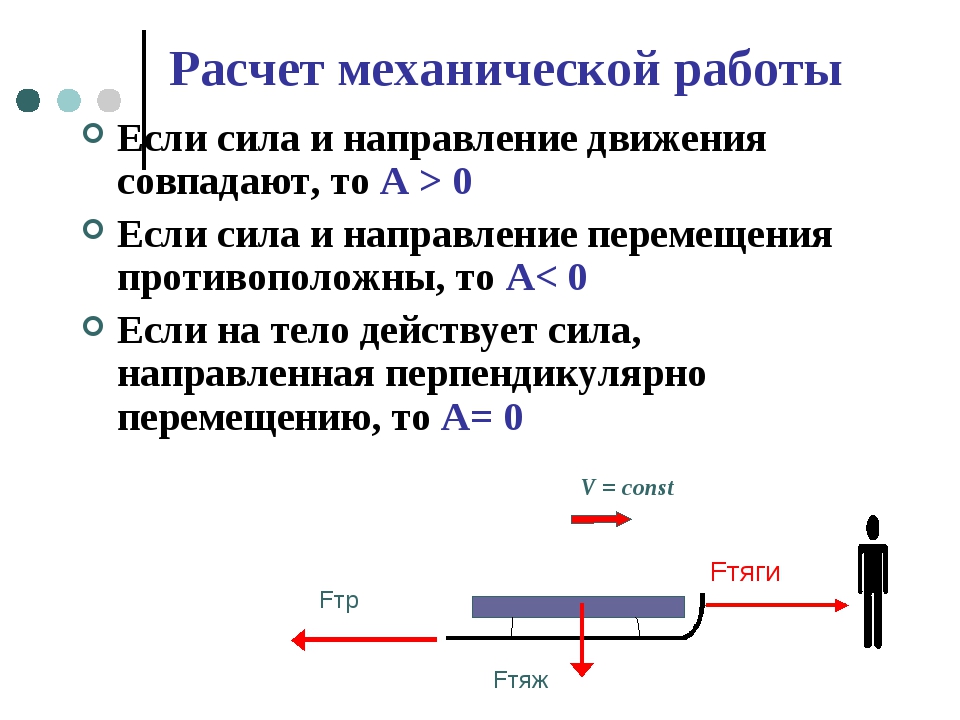
Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.

Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.

Примеры расчёта работы отдельных сил:

Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела: A = mg(h1 – h2)

По замкнутой траектории работа силы тяжести равна нулю.Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна

Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –F_трl , где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю!

Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: .

Мощность показывает, какая работа совершается за 1 с.
Единица измерения мощности в СИ – ватт: = Дж/с = Вт.
Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.

Может пригодиться! 1 л. с

(лошадиная сила) ~ 735 Вт.Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим

Для равноускоренного движения (F = const) где ʋ_ср– средняя скорость движения за расчётный промежуток времени.

Конспект урока «Механическая работа. Механическая мощность».

Следующая тема: «Кинетическая и потенциальная энергия» (код ОГЭ 1.17)

Физическая формула КПД

Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.

Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.

В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.

Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.

Итак, формула КПД:

Ƞ=А/Q, где

A — полезная работа, которую выполняет система.
Q — энергия, которую потребляет система.

Примечания

Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения ds→{\displaystyle {\vec {ds}}}, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях ds→{\displaystyle {\vec {ds}}} суммируется, что и дает в результате интеграл.
Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
По сути через предыдущий, поскольку здесь F→(t)=F→(r→(t)){\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))}; вектор же малого перемещения ds→{\displaystyle {\vec {ds}}} совпадает с dr→{\displaystyle d{\vec {r}}}.
Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫PdV{\displaystyle \int PdV} давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Работа как физическая величина

Отвечая на вопрос, что такое работа в физике, следует уточнить, что это энергия, которая затрачена на совершение каких-либо действий. Например, человек переносит груз с одного места на другое, при этом он совершает работу против сил трения. Если же этот человек начнет поднимать груз, то его работа будет направлена на преодоление силы тяготения планеты. Другой пример: газ, находящийся под поршнем, в результате нагрева начинает увеличивать свой объем, в таком случае говорят, что он совершает некоторую работу.

Во всех перечисленных случаях присутствует одна общая черта: работа отличается от нуля только тогда, когда имеется какой-либо тип механического перемещения объектов или их частей (движение рабочего с грузом, расширение газа).

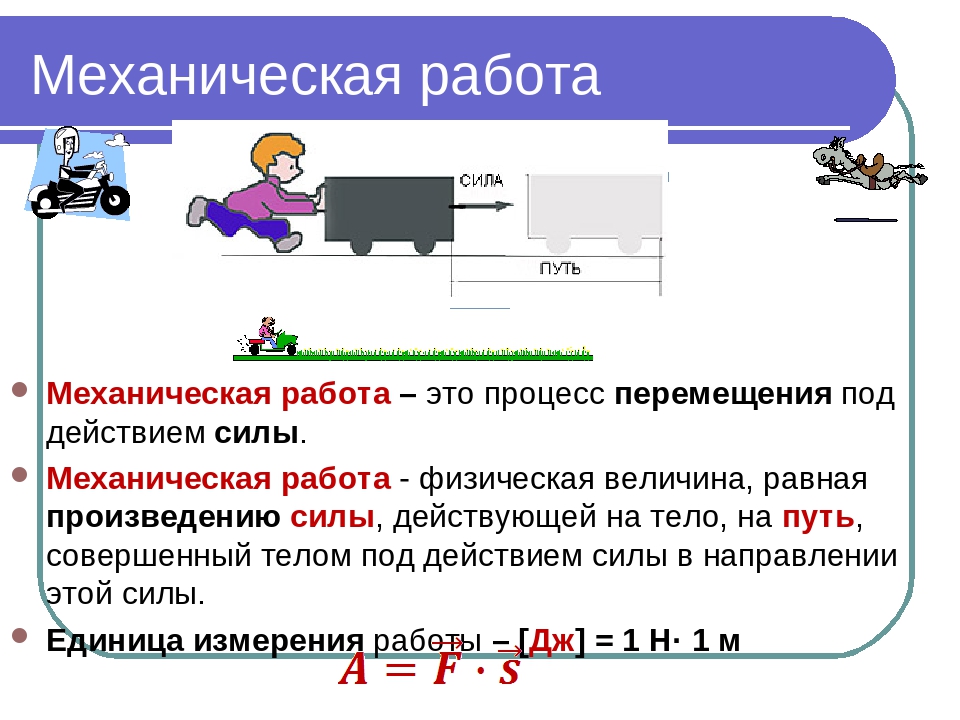
Таким образом, работа — это процесс перевода энергии из одного состояние в другое для данного тела, в результате которого это тело изменяет положение в пространстве.

Что такое КПД

Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.

Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию. Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.

Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.

Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.

Применение в разных сферах физики

Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.

Рассмотрим несколько из примеров процессов с наличием КПД.

К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.

Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.

Примечания

Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193-194. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения ds→{\displaystyle {\vec {ds}}}, на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введённым выше. Затем работы на всех этих перемещениях ds→{\displaystyle {\vec {ds}}} суммируется, что и даёт в результате интеграл.
Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
По сути через предыдущий, поскольку здесь F→(t)=F→(r→(t)){\displaystyle {\vec {F}}(t)={\vec {F}}({\vec {r}}(t))}; вектор же малого перемещения ds→{\displaystyle {\vec {ds}}} совпадает с dr→{\displaystyle d{\vec {r}}}.
Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле ∫PdV{\displaystyle \int PdV} давление подразумевается одинаковым по всему объёму (что часто выполняется в термодинамике, поскольку речь там часто идёт о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведёт к необходимому усложнению формулы, если мы захотим применить её к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Что нужно, чтобы поступить

1. Решите, хотите ли вы идти в науку — заниматься исследованиями и научной работой или вам нужна прикладная специальность. Это поможет с выбором конкретного вуза.

2. Определитесь с направлением: ядерная физика, оптика, радиофизика, наноматериалы или электроника. Постарайтесь сузить круг ваших интересов, это поможет выбрать направление и профиль. Займитесь этим заранее — до сдачи ЕГЭ и поступления.

3. Выберите все подходящие вузы с нужной специальностью. Определиться нужно ещё до выбора ЕГЭ. Расспросите знакомых, используйте специальные сайты для подбора вуза.

4. Какие экзамены нужно сдавать. Для поступления на физические специальности вам понадобится:

Профильная математика
Русский язык
Физика

Приоритет при равенстве баллов будет иметь ваш результат по физике.

5. Олимпиады. Есть Всероссийская олимпиада школьников по физике. Кроме неё есть 19 олимпиад разного уровня, которые можно найти в перечне олимпиад Минобрнауки. Победа в олимпиадах существенно увеличивает шанс попасть в хороший вуз, а в некоторых случаях и вовсе обойти ЕГЭ.

Примеры расчета КПД

Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.

Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.

Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.

Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж

Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если Atotal{\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершенных приложенными к частице силами, то она выражается как:

Atotal=Δ(mv22)=ΔEk,{\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}

где Ek{\displaystyle E_{k}} называется кинетической энергией. Для материальной точки кинетическая энергия определяется как половина произведения массы этой точки на квадрат её скорости и выражается как:

Ek=12mv2.{\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Определение

Работа силы, приложенной к материальной точке

Суммарная работа по перемещению одной материальной точки, совершаемая несколькими силами, приложенными к этой точке, определяется как работа равнодействующей этих сил (их векторной суммой). Поэтому дальше будем говорить об одной силе, приложенной к материальной точке.

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

A=Fss=Fs cos(F,s)=F→⋅s→{\displaystyle A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}}

Здесь точкой обозначено скалярное произведение, s→{\displaystyle {\vec {s}}} — вектор перемещения; подразумевается, что действующая сила F→{\displaystyle {\vec {F}}} постоянна в течение времени, за которое вычисляется работа.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как по траектории точки:

A=∫F→⋅ds→.{\displaystyle A=\int {\vec {F}}\cdot {\vec {ds}}.}

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений ds→,{\displaystyle {\vec {ds}},} если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат, интеграл определяется следующим образом:

A=∫r→r→1F→(r→)⋅dr→{\displaystyle A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot {\vec {dr}}},

где r→{\displaystyle {\vec {r}}_{0}} и r→1{\displaystyle {\vec {r}}_{1}} — радиус-векторы начального и конечного положения тела соответственно.

Следствие. Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа (этой силы) равна нулю.

Работа сил, приложенных к системе материальных точек

Работа сил по перемещению системы материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой).

Даже если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

Эти определения могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Мощность

Сила, приводящая в движение тело, совершает механическую работу

Но как совершается эта работа, быстро или медленно, иногда очень важно знать на практике. Ведь одна и та же работа может быть совершена за разное время

Работу, которую выполняет большой электромотор, может выполнить и маленький моторчик. Но ему для этого понадобится гораздо больше времени.

В механике существует величина, характеризующая быстроту выполнения работы. Эта величина называется мощностью.

Мощность – это отношение работы, выполненной за определённый промежуток времени, к величине этого промежутка.

N = A/∆t

По определению А = F·s·cosα, а s/∆t = v, следовательно

N = F · v · cosα = F · v,

где F– сила, vскорость, α – угол между направлением силы и направление скорости.

То есть мощность – это скалярное произведение вектора силы на вектор скорости движения тела.

В международной системе СИ мощность измеряется в ваттах (Вт).

Мощность в 1 ватт – это работа в 1 джоуль (Дж), совершаемая за 1 секунду (с).

Мощность можно увеличить, если увеличить силу, совершающую работу, или скорость, с которой эта работа совершается.

< Назад
Вперёд >

Работа в термодинамике

Основная статья: Термодинамическая работа

В термодинамике работа, совершённая газом при расширении, рассчитывается как интеграл давления по объёму:

A1→2=∫V1V2PdV.{\displaystyle A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV.}

Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

dA=PdSh.{\displaystyle dA=PdSh.}

Единицы измерения

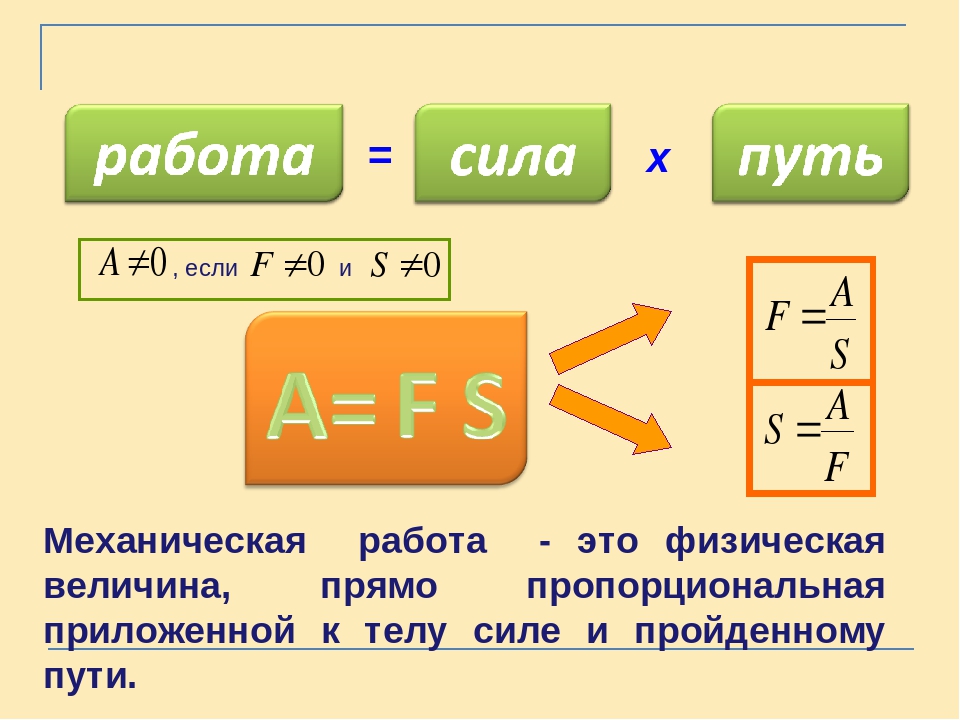
Посмотрим на определяющую формулу A=F*s. =Н*м=Дж. Н — это ньютоны, Дж — джоули. Как понять, что из себя представляет 1 джоуль? Нарисуем схему, на которой изобразим силу, совершающую работу в один джоуль.

На рисунке показано первоначальное и конечное положение тела. Мы переместили его на расстояние 1 м. При перемещении к телу была приложена сила в один ньютон. А=1 Н*1 м=1 Дж. То есть один джоуль — это работа, совершаемая силой в один ньютон при перемещении тела, на расстоянии 1 м в направлении действия силы.

Один джоуль — это небольшая работа. Чтобы поднять килограммовую гирю на 10 см, нужно совершить работу в 1 джоуль. Чтобы поднять ее на метровую высоту, нужно совершить работу в 10 джоулей. Если говорить о работе подъемных кранов, то они поднимают тонны на десятки метров. Поэтому используют и другие единицы измерения работы: килоджоули, мегаджоули и т. д. 1 кДж=1000 Дж, 1 МДж=10^6 Дж. Стрелку настенных часов приводит в движения мотор. Он совершает работу, гораздо меньшую, чем один джоуль. Ее измеряют в милиджоулях. 1 мДж=0,001 Дж. Существуют и микроджоули. 1 мкДж=1*10^-6 Дж.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаемся выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если Atotal{\displaystyle A_{total}} — полная работа, совершённая над частицей, определяемая как сумма работ, совершённых приложенными к частице силами, то она выражается как:

Atotal=Δ(mv22)=ΔEk,{\displaystyle A_{total}=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k},}

Ek=12mv2.{\displaystyle E_{k}={\frac {1}{2}}mv^{2}.}