Переменные и постоянные величины

Квадратные неравенства

Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

y = ax2 + bx + c — это квадратичная функция. Ее мы можем решить с помощью дискриминанта, либо используя теорему Виета. Вспомним, как решаются подобные уравнения:

1) y = x2 + 12x + 11 — функция является параболой. Ее ветви направлены вверх, так как знак коэффициента «a» положительный.

2) x2 + 12x + 11 = 0 — приравниваем к нулю и решаем с помощью дискриминанта.

a = 1, b = 12, c = 11

D = b2 — 4ac= 144 — 44 = 100 > 0, 2 корня

По формуле корней квадратного уравнения получаем:

x₁= -1, x₂= -11

Или можно было решить это уравнение по теореме Виета:

x₁+ x₂= -b/a, x₁+ x₂= -12

x₁x₂= c/a, x₁x₂= 11

Методом подбора получаем такие же корни уравнения.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

-x + 5y = 8 , при y = 1

-x + 5 = 8

Решаем получившееся уравнение и находим икс.

-x = -5 + 8

-x = 3

x = -3

Главное в решении системы — правильно записать ответ. Многие школьники делают ошибку и пишут:

Ответ: -3, 1.

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

(-3; 1)

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

x4 + 15×2 + 7 = 0

За x2 принимаем некое k, и уравнение приобретает понятный вид:

x2 = k, при k ≥ 0

k2 + 15k + 7 = 0

Вот какую пользу в математику несет введение переменных.

Переменные в математике

В математике переменной может быть как реальная измеримая физическая величина, так и некая абстрактная величина, прямо не связанная с процессами реального мира.

В математическом анализе и большинстве смежных разделов математики под переменной x{\displaystyle x} понимают каждый элемент некоторого множества, состоящего, например, из вещественных чисел. Фиксированный элемент этого множества называется значением переменной. Само множество называется областью изменения переменной.

Задание области изменения переменной эквивалентно заданию самой переменной.

Переменные обозначаются малыми буквами латинского или греческого алфавита (возможно, с индексами): x, y, ε.{\displaystyle x,~y,~\varepsilon .}
Области изменения соответствующих переменных обозначаются обычно теми же символами, взятыми в фигурные скобки: {x}, {y}, {ε}{\displaystyle \left\{x\right\},~\left\{y\right\},~\left\{\varepsilon \right\}}.

При моделировании процессов переменные необходимо отличать от параметров, несмотря на то, что переменная в одном контексте может быть параметром в другом.

В прикладной статистике переменная — оценочный фактор или характеристика, индивидуальный или системный атрибут, изменение которых ожидается с течением времени или между отдельными лицами, например переменная возраст.

Переменная и неизвестное

Нужно отметить, что аналогично переменным обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах, например в уравнении 2x=6{\displaystyle 2x=6}, где буквой x{\displaystyle x} обозначено неизвестное, а не переменная, хотя эти понятия весьма схожи и зависят от контекста.

Суть различия между этими понятиями можно пояснить так.

Запись 2x=6{\displaystyle 2x=6} можно, с одной стороны, трактовать как утверждение о возможности найти значение неизвестного x{\displaystyle x}. В этом случае x{\displaystyle x} — обозначение неизвестного числа.

С другой стороны запись 2x=6{\displaystyle 2x=6} можно трактовать как предикат, принимающий значение «истина» при одних значениях x{\displaystyle x}, и значение «ложь» при других. В этом случае x{\displaystyle x} — переменная. На её место в выражении могут подставляться различные значения с целью определения логического (булева) значения записанного предиката.

История

В середине XVII века Рене Декарт в своей «Геометрии» предложил использовать для известных параметров начальные буквы алфавита: a,b,c…,{\displaystyle a,b,c\dots ,} а для неизвестных — последние буквы: x,y,z.{\displaystyle x,y,z.}
Декарт не объяснял свой выбор. Некоторые историки пытались объяснить выбор буквы x{\displaystyle x} в качестве неизвестной. Так, например, словарь Уэбстера (1909—1916) утверждал, что переменная x{\displaystyle x} появилась как транскрипция арабской буквы ش — первой буквой в слове شيء‎, которое переводится на русский языка как «что-то», «нечто». Тем не менее эта и другие подобные версии не находят подтверждений и игнорируют тот факт, что Декарт использовал наряду с x{\displaystyle x} еще y{\displaystyle y} и z{\displaystyle z}.

Декарт считал значения переменных всегда неотрицательными, а отрицательные величины отражал знаком «минус» перед переменной. Если знак коэффициента был неизвестен, Декарт ставил многоточие. Нидерландский математик Иоганн Худде уже в 1657 году позволил буквенным переменным принимать значения любого знака.

Ф. Кэджори характеризует декартовскую запись степеней как самую удачную и гибкую символику во всей алгебре — она не только облегчает преобразования, но стимулировала расширение понятия возведения в степень на отрицательные, дробные и даже комплексные показатели, а также появление в математике степенной и показательной функции; все эти достижения трудно было бы осуществить при использовании обозначений XVI века

Основные математические величины

Дети в школе, изучая величины в математике, к 4 классу уже имеют широкое представление о таких значениях, как длина, масса, объем, площадь, скорость и время.

Под длиной предмета принято понимать характеристику линейного размера. Ее измеряют в миллиметрах, сантиметрах, дециметрах, метрах и километрах. Эту тему в школе дети проходят, начиная с первого класса.

Масса предмета — еще одна физическая величина, измеряемая в основном граммами и килограммами. А также объем тел, который исчисляется литрами и миллилитрами. Однако не стоит вводить ребенка в заблуждение и считать массу и вес равными понятиями. Масса — это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле.
Под площадью геометрической фигуры принято понимать занимаемое ею пространство на плоскости, которое исчисляется в мм2, см2, дм2, м2 и км2.
Время — понятие довольно относительное и для человека связано с его ощущениями, его нельзя увидеть, но можно почувствовать в смене дня, ночи и времен года. Поэтому для знакомства детей с понятием времени используют точные приборы, такие как песочные часы и часы со стрелкой. Время исчисляется секундами, минутами, часами, днями, годами и так далее.

На основании пройденной темы о времени и длине дети изучают понятие скорости. По сути, скорость — это отрезок пути, пройденный за некоторое время.

Русская система измерения

С Древней Руси до принятия в Российской империи метрической системы мер принято было производить замеры с помощью длины локтя, ширины ладони, длины стопы — фут. Расстояние от кончика вытянутой вверх руки до пятки противоположной ноги называлось сажень, расстояние между вытянутыми руками — маховая сажень и т. д. Для измерения расстояния брали, например, слышимость петушиного крика или способность лошади без отдыха добраться из пункта А в пункт Б. Так люди измеряли дальность проложенного маршрута.

Даже сейчас в пословицах и поговорках мы можем встретить напоминания о существовании старинных величин. Об этом свидетельствую такие выражения, как «слышать за версту», «косая сажень в плечах», «мерить на свой аршин» и другие крылатые фразы.

В 1899 году, 4 июня была принята единая метрическая система, которая являлась необязательной. Обязательной она стала 14 сентября 1918 года уже при советской власти, практически сразу после Великой октябрьской революции.

Виды величин

Под величиной имеется в виду то, что выражает свойства определенного предмета, вещества или явления. К примеру, температура воздуха, масса животного, процентное содержание витаминов в таблетке — это все величины, числовые значения которых можно вычислить.

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

Возьмем прямолинейное равномерное движение. Точка в пространстве движется с одинаковой скоростью на каждом промежутке времени. То есть изменяются время и расстояние, а скорость остается одинаковой. В данном примере время и расстояние — переменные величины, а скорость — постоянная.

Или, например, “пи”. Это иррациональное число, которое продолжается без повторяющейся последовательности цифр и не может быть записано полностью, поэтому в математике оно выражается общепринятым символом, который принимает только значение данной бесконечной дроби. То есть “пи” — это постоянная величина.

Функция

В научных исследованиях, при решении практических задач всегда рассматривают изменения одних величин в зависимости от изменений других. Например, в электрической цепи величина тока меняется в зависимости от величины сопротивления, объем шара меняется в зависимости от его радиуса и т.д.

При этом в различных физических явлениях те или иные величины могут вести себя по-разному. Например, пр равномерном движении пройденное расстояние меняется в зависимости от времени, а скорость остается постоянной. А вот при равноускоренном движении в зависимости от времени меняется не только расстояние, но и скорость.

Взаимосвязь изменяемых величин в математике описывают с помощью функций.

Формальное определение выглядит следующим образом. Пусть существует некоторый закон $f$, по которому каждому числовому значению переменной $x$ ставится в соответствие единственное определенное числовое значение другой переменной $y$. Такой закон называется функцией от $x$ и символически записывается в виде $y=f\left(x\right)$.

При этом переменную $x$ называют независимой переменной или аргументом, переменную $y$ — зависимой переменной или функцией.

Таким образом, буква $f$ в записи $y=f\left(x\right)$ обозначает правило или совокупность действий, которые нужно произвести над значением аргумента $x$, чтобы получить значение функции $y$. Вместо буквы $f$ можно использовать и любые другие, например, $y=F\left(x\right)$, $y=\$ \left(x\right)$ и т.д. Достаточно часто пишут и так: $y=y\left(x\right)$.

Предположим, что существует совокупность значений аргумента $x$, для которой, используя правило $f$, можно определить соответствующую совокупность значений функции $y$. Такую совокупность значений аргумента $x$ называют областью определения функции $y=f\left(x\right)$, а совокупность значений $y$ называют областью значений функции $y=f\left(x\right)$.

Таким образом, чтобы задать функцию, необходимо задать для неё правило вычисления $f$, а также указать область её определения.

Определение слова «Переменная» по БСЭ:

Переменная — переменное, одно из основных понятий математики и логики. Начиная с работ П. Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников «высшей» математики под П. понимали некоторую«величину», которая может «изменяться», принимая в процессе этого изменения различные «значения». Тем самым П. противопоставлялись «постоянным» (или константам) — числам или каким-либо др. «величинам»,каждая из которых имеет единственное, вполне определённое значение (см. Переменные и постоянные величины). По мере развития математики и в ходе её обоснования представления о «процессах», «изменении величин» и т. п. тщательно изгонялись из математического арсенала как«внематематические», в результате чего П. стала пониматься как обозначение для произвольного элемента рассматриваемой предметной области (например, области натуральных чисел или действительных чисел), то есть как родовое имя всей этой области (в отличие от констант — «собственных имён» для чисел или др. конкретных предметов рассматриваемой области).Этот пересмотр взглядов на понятие П. был тесно связан с перестройкой математики на базе множеств теории, завершившейся в конце 19 в. При всей простоте и«естественности» такой перестройки она существенным образом опирается на так называемую абстракцию актуальной бесконечности, позволяющую рассматривать произвольные бесконечные множества в качестве «данных» («завершенных», «готовых», «актуальных»)объектов и применять по отношению к ним любые средства классической логики, отвлекаясь от незавершённости и принципиальной незавершимости процесса образования такого множества. Трудности решения логических проблем, связанных с принятием этой абстракции, делают понятной частичную«реабилитацию» старинных представлений о «переменных величинах». при построении математических теорий представители некоторых школ (см. Математический интуиционизм, Конструктивное направление) предпочитают обходиться боле (слабой, но зато менее уязвимой в логическом отношении абстракцией потенциальной осуществимости, с точки зрения которой с бесконечными множествами как раз связываются представления о процессах их«порождения»,- сколь угодно далеко заходящих, но никогда не завершающихся (см. Бесконечность в математике). При исследовании вопроса непротиворечивости различных областей математики на такую позицию фактически встаёт значительное большинство математиков и логиков (см. Метаматематика).В формализованных языках (исчислениях, формальных системах) математической логики П. называются символы строго фиксированного вида, могущие при определённых условиях заменяться выражениями данного исчисления. Это относится к так называемым свободным (или значащим) П. примером которых может служить П. в неравенстве x > 5, обращающемся при подстановке вместо x, скажем, цифры 7 (то есть обозначения для числа) 7 в истинное высказывание, а при подстановке цифры 2 — в ложное высказывание

Что касается так называемых связанных (или фиктивных) П., то они сами по себе вообще ничего не означают, несут чисто синтаксические функции и могут (при соблюдении некоторых элементарных предосторожностей)«переименовываться», то есть заменяться др. П

Такова, например, П. y в записях

25&sum.y=1

или

&forall.y P (y),

интерпретации(прочтения)любойпервая

25&sum.x=1

или

25&sum.z=1

z ,

втораяможно(согласноподставлятьсоответственнопониматьопределенныйвхождениявыраженияформулыупотреблениюместоименийПерваяприменениюформула₁_nнекоторыйместныйПредикатинтерпретироватьсяпредложение(Высказывание),именно₁_n₁_nвсеобщностиформулировкенаконец,приписыватьсясовокупноститогдаусловнойНапример,уравнениикогдаформализацииуточнениеиспользованиятакжеКвантор,ЛогикаКлиниВведениеметаматематику,

Переменные в программировании

Основная статья: Переменная (программирование)

В языках программирования переменная реализуется как некоторая область машинной памяти, на которую указывает идентификатор переменной.

Машинная переменная принадлежит одному из типов данных и имеет некоторый допустимый диапазон значений, которые она может принимать. Например, логическая (булевская) переменная может принимать только два значения, — «истина» и «ложь», допустимые диапазоны изменения целых и вещественных переменных зависят от конкретного компилятора и платформы исполнения.

В высокоуровневых языках программировании, переменные, как правило, обозначаются произвольной последовательностью символов из букв и цифр — словом, обязательно начинающегося с буквы, например, «time», «x12», «foo».

Такое понятие переменной в некотором смысле схоже с математическим. Математики в XVII веке уже использовали переменную, чтобы «забронировать» в формуле место, на которое можно подставлять конкретные значения. Буквенные обозначения резервируют и именуют области этой памяти. Если формула в математике является алгоритмом вычисления, то понятие переменной совпадает с понятием переменной в программировании.

Если формула используется только для выражения отношения между элементами множеств, то нет необходимости в понятии переменных как ячеек памяти.

Неравенства, примеры решения

Неравенство представляет собой запись, в которой два математических выражения или два числа связаны знаками сравнения: <, >, ≤, ≥. Они бывают строгими и обозначаются знаками < и > или нестрогими со знаками ≤, ≥.

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.

Решить неравенство — значит найти все допустимые значения переменной.

Пример с одной переменной:

10x — 50 > 150

Решаем, как обычное линейное уравнение — переносим слагаемые с переменной влево, без переменной — вправо и приводим подобные члены:

10x > 200

Делим обе части неравенства на 10 и получаем:

x > 20

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

6x — 12 ≥ 18

6x ≥ 30

x ≥ 5

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

x ∈ [5; +∞)

Обозначение

В математике переменные обычно обозначаются одной буквой. Однако за этой буквой часто следует нижний индекс, как в x ₂ , и этот нижний индекс может быть числом, другой переменной ( x _i ), словом или сокращением слова ( x _in и x _out ) и даже математическое выражение . Под влиянием информатики можно встретить в чистой математике имена переменных, состоящие из нескольких букв и цифр.

Вслед за французским философом и математиком 17 века Рене Декартом буквы в начале алфавита, например, a , b , c , обычно используются для известных значений и параметров, а буквы в конце алфавита, например x , y , z , и t обычно используются для неизвестных и переменных функций. В печатной математике , как правило, переменные и константы выделяются курсивом .

Например, общая квадратичная функция условно записывается как:

аИкс2+бИкс+c,{\ displaystyle ax ^ {2} + bx + c \ ,,}

где a , b и c — параметры (также называемые константами, потому что они являются постоянными функциями ), а x — переменная функции. Более явный способ обозначить эту функцию —

Икс↦аИкс2+бИкс+c,{\ Displaystyle х \ mapsto ax ^ {2} + bx + c \ ,,}

который очищает статус функции-аргумента x и, таким образом, неявно константный статус a , b и c . Поскольку c встречается в члене, который является постоянной функцией от x , он называется постоянным членом .

Конкретные разделы и приложения математики обычно имеют особые соглашения об именах переменных. Переменным с похожими ролями или значениями часто присваиваются последовательные буквы. Например, три оси в трехмерном координатном пространстве условно называются x , y и z . В физике имена переменных в значительной степени определяются физической величиной, которую они описывают, но существуют различные соглашения об именах. Соглашение, которому часто следуют в области вероятности и статистики, состоит в том, чтобы использовать X , Y , Z для имен случайных величин , сохраняя x , y , z для переменных, представляющих соответствующие фактические значения.

Есть много других способов обозначения. Обычно переменные, которые играют аналогичную роль, представлены последовательными буквами или одной и той же буквой с разными нижними индексами . Ниже приведены некоторые из наиболее распространенных вариантов использования.

a , b , c и d (иногда расширенные до e и f ) часто представляют параметры или коэффициенты .
a , a ₁ , a ₂ , … играют аналогичную роль, в противном случае потребовалось бы слишком много разных букв.
a _i или u _i часто используются для обозначения i-го члена последовательности или i-го коэффициента ряда .
f и g (иногда h ) обычно обозначают функции .
i , j и k (иногда l или h ) часто используются для обозначения различных целых чисел или индексов в индексированном семействе . Они также могут использоваться для обозначения единичных векторов .
l и w часто используются для обозначения длины и ширины фигуры.
l также используется для обозначения линии. В теории чисел l часто обозначает простое число, не равное p .
n обычно обозначает фиксированное целое число, такое как количество объектов или степень уравнения
Когда нужны два целых числа, например, для размеров матрицы , обычно используются m и n .

.
p часто обозначает простые числа или вероятность .
q часто обозначает степень простого или частное
r часто обозначает радиус , остаток или коэффициент корреляции .
t часто обозначает время .
x , y и z обычно обозначают три декартовых координаты точки в евклидовой геометрии . По сути, они используются для обозначения соответствующих осей .
z обычно обозначает комплексное число или, в статистике, нормальную случайную величину .
α , β , γ , θ и φ обычно обозначают угловые меры.
ε

ε и δ обычно обозначают два небольших положительных элемента.

обычно представляет собой сколь угодно малое положительное число.
λ используется для собственных значений .
σ часто обозначает сумму или, в статистике, стандартное отклонение .

Математические операции

Основные особенности математических операций таковы:

знаки операций могут быть указаны с помощью специальных символов, а также с помощью специально оговоренных слов;
операции могут быть унарными (выполняемыми над одним операндом) и бинарными (выполняемыми над двумя операндами);
для операций установлены четыре уровня приоритетов, определяющих порядок вычисления выражения.

Таблица знаков некоторых операций и уровней приоритетов

Правила вычисления сложного выражения, содержащего цепочку операций при отсутствии регулирующих скобок, следующие:

cначала вычисляются значения всех функций;
затем поочерёдно выполняются операции в порядке убывания их приоритета;
операции равного приоритета выполняются по порядку слева направо.

При наличии регулирующих скобок выражение содержит составные операнды, значения которых должны быть вычислены в первую очередь.

Некоторые особенности записи математических выражений:

не рекомендуется пропускать знаки операций, хотя во многих случаях можно пропустить знак умножения;
аргументы функций желательно указываться в круглых скобках;
указание подряд двух и более знаков бинарных операций недопустимо; формально допустимо использование нескольких знаков унарных операций подряд, в том числе и вместе с бинарной.

Понятие переменной

Для начала узнаем, что такое переменная? Это численная величина, которая может принимать множество значений. Она не может быть постоянной, так как в разных задачах и уравнениях для удобства решения мы принимаем за переменную разные числа, то есть, например, z — это общее обозначение для каждой из величин, за которые ее принимают. Обычно их обозначают буквами латинского или греческого алфавита (x, y, a, b и так далее).

Есть разные виды переменных. Ими задаются как некоторые физические величины — путь (S), время (t), так и просто неизвестные значения в уравнениях, функциях и других выражениях.

Например, есть формула: S = Vt. Здесь переменными обозначаются определенные величины, имеющие отношение к реальному миру — путь, скорость и время.

А есть уравнение вида: 3x — 16 = 12x. Здесь уже за x принимается абстрактное число, которое имеет смысл в данной записи.

Неравенства, примеры решения

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.

Решить неравенство — значит найти все допустимые значения переменной.

Пример с одной переменной:

10x — 50 > 150

10x > 200

Делим обе части неравенства на 10 и получаем:

x > 20

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

6x — 12 ≥ 18

6x ≥ 30

x ≥ 5

x ∈ [5; +∞)

Квадратные неравенства

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

2) x2 + 12x + 11 = 0 — приравниваем к нулю и решаем с помощью дискриминанта.

a = 1, b = 12, c = 11

D = b2 — 4ac= 144 — 44 = 100 > 0, 2 корня

По формуле корней квадратного уравнения получаем:

x₁= -1, x₂= -11

Или можно было решить это уравнение по теореме Виета:

x₁+ x₂= -b/a, x₁+ x₂= -12

x₁x₂= c/a, x₁x₂= 11

Методом подбора получаем такие же корни уравнения.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

x4 + 15×2 + 7 = 0

За x2 принимаем некое k, и уравнение приобретает понятный вид:

x2 = k, при k ≥ 0

k2 + 15k + 7 = 0

Вот какую пользу в математику несет введение переменных.

Генезис и эволюция концепции

В 7 веке Брахмагупта использовал разные цвета для представления неизвестных в алгебраических уравнениях в Брахмаспхунасиддханте . Один из разделов этой книги называется «Уравнения нескольких цветов».

В конце 16-го века Франсуа Виет представил идею представления известных и неизвестных чисел буквами, в настоящее время называемые переменными, и идею вычисления с ними, как если бы они были числами, — чтобы получить результат простой заменой. Соглашение Виэта заключалось в использовании согласных для известных значений и гласных для неизвестных.

В 1637 году Рене Декарт «изобрел соглашение о представлении неизвестных в уравнениях через x , y и z , а известных через a , b и c ». Вопреки соглашению Виэта, слово Декарта все еще широко используется.

Начиная с 1660-х годов Исаак Ньютон и Готфрид Вильгельм Лейбниц независимо друг от друга разработали исчисление бесконечно малых , которое, по сути, состоит в изучении того, как бесконечно малое изменение переменной величины вызывает соответствующее изменение другой величины, которая является функцией первой переменной. Почти столетие спустя Леонард Эйлер закрепил терминологию исчисления бесконечно малых и ввел обозначение y = f ( x ) для функции f , ее переменной x и значения y . До конца XIX века слово « переменная» относилось почти исключительно к аргументам и значениям функций.

Во второй половине 19 века выяснилось, что основы исчисления бесконечно малых не были достаточно формализованы, чтобы иметь дело с очевидными парадоксами, такими как нигде не дифференцируемая непрерывная функция . Чтобы решить эту проблему, Карл Вейерштрасс ввел новый формализм, состоящий в замене интуитивного понятия предела формальным определением. Старое понятие предела было «когда переменная x изменяется и стремится к a , затем f ( x ) стремится к L », без какого-либо точного определения «имеет тенденцию». Вейерштрасс заменил это предложение формулой

(∀ϵ>)(∃η>)(∀Икс)|Икс-а|<η⇒|L-ж(Икс)|<ϵ,{\ Displaystyle (\ forall \ epsilon> 0) (\ существует \ eta> 0) (\ forall x) \; | xa | <\ eta \ Rightarrow | Lf (x) | <\ epsilon,}

в котором ни одна из пяти переменных не считается изменяющейся.

Эта статическая формулировка привела к современному понятию переменной, которая представляет собой просто символ, представляющий математический объект, который либо неизвестен, либо может быть заменен любым элементом данного набора (например, набором действительных чисел ).

Метод интервалов

Второй способ — это метод интервалов. Алгоритм его решения:

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

Решим неравенство (x — 4)(x — 5)(x + 7) ≤ 0

1) Нули неравенства: 4, 5 и -7.

2) Изображаем их на числовой прямой.

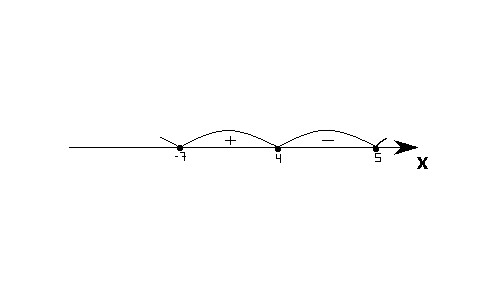
3) Определяем знаки интервалов.

Ответ: (-∞; -7]; .

Решим еще одно неравенство: x2(3x — 6)(x + 2)(x — 1) > 0

1. Нули неравенства: 0, 2, -2 и 1.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Прямая делится на промежутки — от -2 до 0, от 0 до 1, от 1 до 2.

Возьмем значение на первом промежутке — (-1). Подставляем в неравенство. При данном значении неравенство становится положительным, значит и знак на этом промежутке будет +.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Ответ: (-2; 0), (1; 2).