Функции и графики - математика - теория, тесты, формулы и задачи - обучение математике, онлайн подготовка к цт и егэ

Метод интервалов. Средний уровень.

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Линейная функция

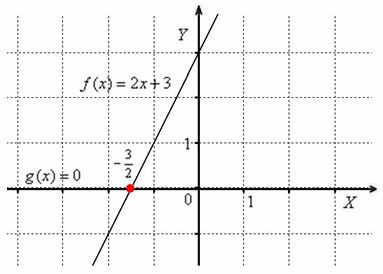
Линейной называется функция вида. Рассмотрим для примера функцию. Она положительна при 3″> и отрицательна при. Точка – нуль функции (). Покажем знаки этой функции на числовой оси:

Говорим, что «функция меняет знак при переходе через точку ».

Видно, что знаки функции соответствуют положению графика функции: если график выше оси, знак « », если ниже – « ».

Если обобщить полученное правило на произвольную линейную функцию, получим такой алгоритм:

Находим нуль функции;
Отмечаем его на числовой оси;
Определяем знак функции по разные стороны от нуля.

Квадратичная функция

Надеюсь, ты помнишь, как решаются квадратные неравенства? Если нет, прочти тему «Квадратные неравенства». Напомню общий вид квадратичной функции: .

Теперь вспомним, какие знаки принимает квадратичная функция. Ее график – парабола, и функция принимает знак « » при таких, при которых парабола выше оси, и « » – если парабола ниже оси:

Если у функции есть нули (значения, при которых), парабола пересекает ось в двух точках – корнях соответствующего квадратного уравнения. Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.

А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?

Вспомним, что квадратный трехчлен можно разложить на множители:

Отметим корни на оси:

Мы помним, что знак функции может меняться только при переходе через корень. Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.

В нашем примере: при 3″> оба выражения в скобках положительны (подставим, например: 0″>). Ставим на оси знак « »:

Ну и, при (подставь, например,) обе скобки отрицательны, значит, произведение положительно:

Это и есть метод интервалов
: зная знаки сомножителей на каждом интервале, определяем знак всего произведения.

Рассмотрим также случаи, когда нулей у функции нет, или он всего один.

Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак. Его легко определить, подставив в функцию.

Если корень только один, парабола касается оси, поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?

Если разложить такую функцию на множители, получатся два одинаковых множителя:

А любое выражение в квадрате неотрицательно! Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:

Такой корень будем называть кратным
.

Полиномиальные корни

Каждый действительный многочлен нечетной степени имеет нечетное число действительных корней (с учетом ); аналогично действительный многочлен четной степени должен иметь четное число действительных корней. Следовательно, действительные нечетные многочлены должны иметь по крайней мере один действительный корень (поскольку наименьшее нечетное целое число равно 1), тогда как четные многочлены могут не иметь ни одного. Этот принцип можно доказать, сославшись на теорему о промежуточном значении : поскольку полиномиальные функции непрерывны , значение функции должно пересекать ноль в процессе изменения с отрицательного на положительное или наоборот (что всегда происходит для нечетных функций).

Основная теорема алгебры

Основная теорема алгебры утверждает, что каждый многочлен степени имеет комплексные корни, считая с их кратностями. Неверные корни многочленов с действительными коэффициентами входят в сопряженные пары. Формулы Виета связывают коэффициенты многочлена с суммами и произведениями его корней.
п{\ displaystyle n}п{\ displaystyle n}

Примеры предложений

Далее приведены предложения, содержащие слово «ноль»:

Если ты считаешь, что я ноль в физике, то посмотри на то, с какой скоростью я решаю самые трудные задачи.
Абсолютный ноль в математике, это когда при любом умножении, делении и сложении в конце все равно получается ноль.
Я получила от Алексея ноль внимания, хотя надеялась на взаимную симпатию ко мне.
«Да ты ноль без палочки, друг мой!» − прокричала мне бабушка, считая, что я пуст и бесполезен.
Ноль кажется пустым, но в то же время чем-то бесконечным и бескрайним, показателем того, насколько Вселенная глубокая.
Если из пятидесяти вычесть пятьдесят, то получится ноль.
Ноль является загадочным числом, одно лишь его написание − загадка.

Новое в блогах

Нуль это процесс… или технология арифметики, алгебры, теории чисел……

Во-первых, ноль или нуль

Прежде чем ответить на поставленный вопрос, предлагаю обратиться к этимологии, т.е к науке, которая правильно толкует слова. Ноль происходит от латинского слова “NULLUS”- никакой, пустой, несуществующий. В русском языке, ноль позаимствовали с немецкого языка,”NULL”. Привезли в Россию “NULL” ученые, во времена Петра I. До петровских времен вычислениями занимались с помощью римских цифр.

Нуль это процесс перехода из положительного в отрицательный и НАОБОРОТ. Ну, или это процесс работы трех триединых процессов — положительный, нейтральный, отрицательный, которые работают в трех триединых формах взаимосвязей — параллельно, последовательно, взаимоувязано.

Поэтому бесконечность и обозначают «лежачей» восьмеркой. Это процесс переходов и сам процесс НЕ прерывается.

Потому следует говорить о трех триединых процессах работы нуля: в арифметическом процессе; в алгебраическом процессе; в процессе теории чисел или трансцедентное число (от лат. Transcendere — переходить, превосходить). Или это триединство элементарное (или монистическое), это триединство простое (диалектическое), триединство сложное или в полной структуре.

Технологий работы Нуля три триединых – арифметическая, алгебраическая, теории чисел.

Нуль в арифметике. (монистическая технология идеалистической предметности) На числовой прямой 0 разделяет положительные и отрицательные числа Начало координат (начало отсчёта) в евклидовом пространстве — особаяточка, обычно обозначаемая буквой О, которая используется как точка отсчёта для всех остальных точек. В евклидовой геометрии начало координат может быть выбрано произвольно в любой удобной точке.

Нуль в алгебре. (технология идеалистической диалектики). Нулева́я ма́трица — это матрица, размера m×n все элементы которой равны нулю. Она обозначается как Z или 0 или 0 m, n

Нулевая матрица, и только она, имеет ранг 0.

Нуль в теории чисел. (технология триединства от идеалистического начала)

Как математическая дисциплина, теория чисел восходит к трудам древнегреческого математика Диофанта Александрийского (предположительно III век до н. э.) в которых изучались задачи решения алгебраических уравнений в целых и рациональных числах. Трансценде́нтное число́ (от лат. Transcendere — переходить, превосходить) – это вещественное или комплексное число, не являющееся алгебраическим — иными словами, число, которое не может быть корнем многочлена с рациональными коэффициентами (не равного тождественно нулю).

Петербургская школа теории чисел, занимает особое место — это Чебышев (как создатель школы), Коркин, Золотарев, Марков, Вороной….

Возрастание и убывание функций

Посмотрим на график произвольной функции:

Видно, что область определения ф-ции – это промежуток .

На графике сначала ф-ция как бы «поднимается». При увеличении х растет значение у. Так происходит до точки (1; 5). После этого ситуация меняется, при увеличении аргумента значение ф-ции начинает падать. В математике принято говорить, что ф-ция возрастает на промежутке и функция убывает на промежутке . Можно сказать и иначе – ф-ция у является возрастающей функцией на множестве и убывающей функцией на множестве .

Рассмотрим это определение возрастающей функции подробнее. Построим произвольную возрастающую ф-цию и выберем на ней две точки со значениями аргумента х₁ и х₂. Также отметим значения ф-ции в этих точках, у(х₁) и у(х₂):

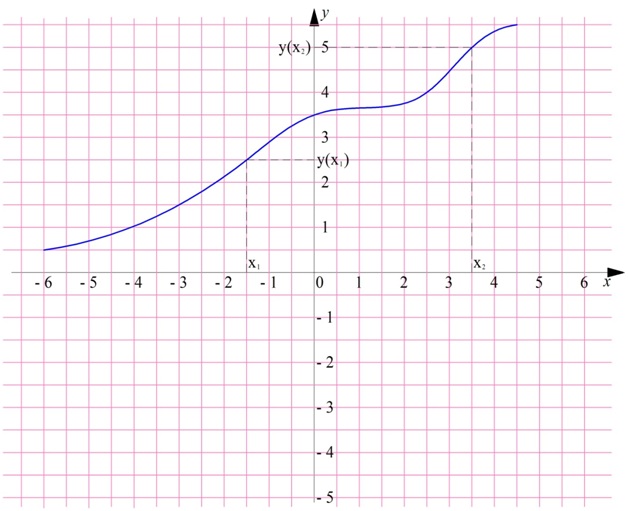
По определению, если х₁ меньше х₂, то и у(х₁) <у(х₂). Другими словами, из двух точек та, которая располагается левее (то есть имеет меньшее значение х), будет одновременно располагаться и ниже, (то есть иметь меньшее значение у).

Мы видим возрастание функции на промежутке . Однако она также будет возрастать и на любом другом промежутке, который является частью отрезка . Например, можно сказать, что она возрастает на промежутке или .

Аналогично дается и определение убывающей ф-ции:

По сравнению с определением возрастающей ф-ции изменился лишь один символ, в последнем неравенстве для у(х₁) иу(х₂) стоит знак «больше» а не меньше. Покажем пример убывания функции.

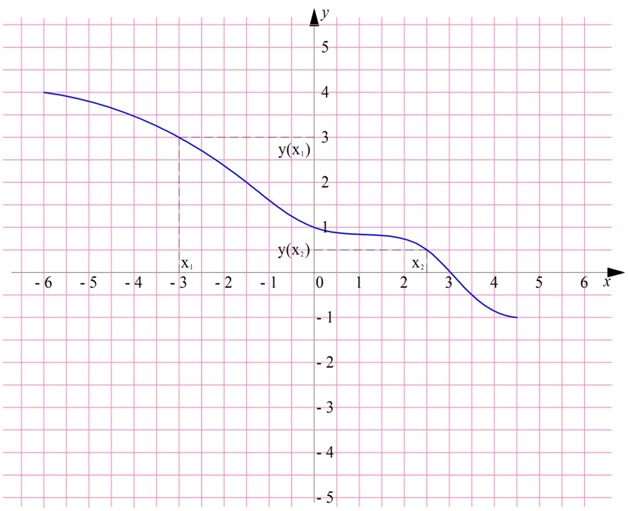
Заметим, что в приведенных определениях используются строгие неравенства со знаками «>»и «<». Однако в математике используются и нестрогие неравенства, содержащие знаки «≤» и «≥». С их использованием можно записать ещё 2 определения:

Приведем пример неубывающей ф-ции:

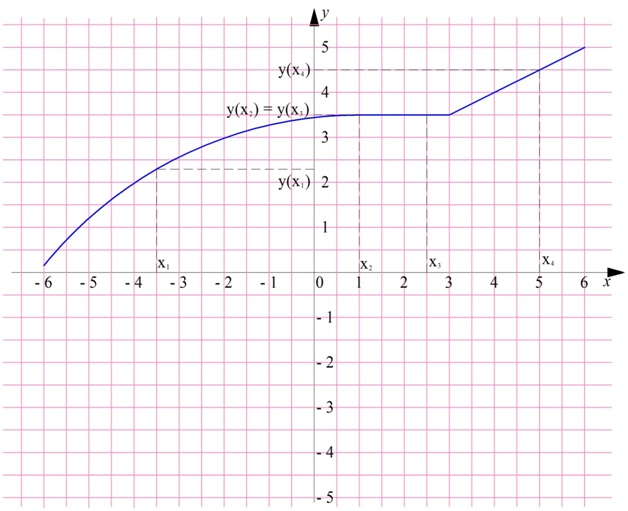
Здесь х₁<x₂<x₃<x₄. Видно, что, например, у(х₁) <у(х₂). Однако у(х₂) = у(х₃). Получается, что на графике ф-ции есть плоская «площадка» на промежутке . Для всех значений х из этого промежутка у = 3,5. Из-за этой площадки ф-цию нельзя считать строго возрастающей.

Теперь покажем пример невозрастающей ф-ции:

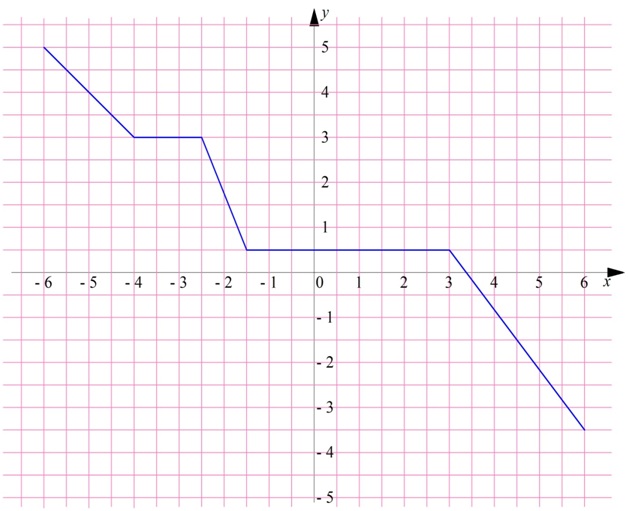
Здесь также есть плоские «площадки», из-за которых ф-цию нельзя считать просто убывающей.

Ясно, что всякая возрастающая ф-ция является неубывающей, а каждая убывающая ф-ция одновременно считается и невозрастающей.

В математике часто вместо всех этих терминов используют понятие монотонности. Дадим определение монотонной функции:

Если же ф-ция убывает или возрастает на промежутке (то есть не имеет плоской площадки), то говорят, что она строго монотонна.

Рассмотрим ф-цию, изображенную на рисунке:

Ф-ция возрастает на промежутках и , а также убывает на промежутках и . Значит, на каждом из этих промежутков ф-ция строго монотонна. На отрезке ф-ция невозрастающая, поэтому здесь она просто монотонна. Любой промежуток, на котором ф-ция монотонна, называют промежутком монотонности.

Различают как промежутки убывания функции, так и промежутки возрастания функции.

Понятно, что если ф-ция строго монотонна, то она и просто монотонна. В большинстве школьных задач не важна строгость монотонности, поэтому слово «строго» часто опускают.

Во всех данных определениях рассматривалось поведение ф-ции на каком-то отдельном числовом промежутке. Одна и та же ф-ция может на одном числовом промежутке возрастать, а на другом убывать. Однако некоторые ф-ции сохраняют свой характер на всей своей области определения. Например, линейная ф-ция у = 2х – 3 возрастает на протяжении всей числовой прямой, то есть на промежутке (– ∞; + ∞):

В большинстве случаев промежутки монотонности ф-ции очевидны, исходя из графика ф-ции. Однако и без их построения можно аналитически доказывать монотонность ф-ции.

Пример. Докажите, что ф-ция у = 2х – 3 возрастает на промежутке (– ∞; + ∞).

Решение. Выберем произвольные числа х₁ и х₂, причем х₁< х₂. Разность (х₂ – х₁) будет, очевидно, положительным числом. Найдем теперь разность (у(х₂) – у(х₁)):

у(х₂) – у(х₁) = (2х₂ – 3) – (2х₁ – 3) = 2х₂– 3 – 2х₁+ 3 = 2х₂ – 2х₁ = 2(х₂ – х₁)

Так как (х₂ – х₁) – положительное число, то и 2(х₂ – х₁), а значит, и (у(х₂) – у(х₁)) – тоже положительное число. Если же разность двух числе положительна, то уменьшаемое больше вычитаемого. Значит, у(х₂) > у(х₁). По определению получаем, что у = 2х – 3 – возрастающая ф-ция.

Онлайн-курсы по математике помогут подготовиться к ОГЭ наилучшим образом

Четные и нечетные функции

При изучении степенных ф-ций мы заметили, что при четном показатели степени n их график симметричен относительно оси Оу:

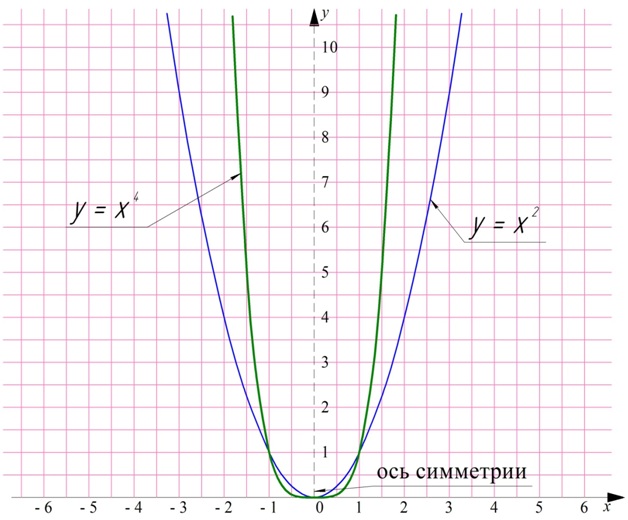
Почему так происходит? Дело в том, что у этих ф-ций противоположным значениям аргументов соответствует одно и то же значение у. Убедимся в этом на примере у = х2:

у(1) = 12 = 1 и у(– 1) = (– 1)2 = 1;
у(2) = 22 = 4 и у(– 2) = (– 2)2 = 4;
у(3) = 32 = 9 и у(– 3) = (– 3)2 = 9.

В общем случае эту особенность можно доказать так:

у(– х) = (– х)2 = х2 = у(х)

В математике есть специальный термин для обозначения ф-ций, обладающих таким свойством. Их называют четным функциями.

Определение четной функции можно записать и так, чтобы в нем фигурировали формулы:

Для проверки того, является ли функция четной, достаточно подставить в нее вместо аргумента х величину (– х).

Пример. Докажите, что ф-ция у = х4 + 3х2 является четной.

Решение. Подставим в ф-цию значение (– х):

у(– х) = (– х)4 + 3(– х)2 = х4 + 3х2

Получили исходную ф-цию у(х). Значит, исследуемая функция является четной.

Пример. Четна ли ф-ция

Решение снова подставим в ф-цию значение (– х):

Получили изначальную ф-цию. Следовательно, она – четная.

Почему же четные ф-ции симметричны относительно оси Оу? Из определения следует, что если графику четной ф-ции принадлежит точка (х;у), то ему же принадлежит точка (– х;у). Посмотрим, как они располагаются на координатной плоскости:

Они симметричны относительно оси Оу. Если же для каждой точки графика есть симметричная точка, также ему принадлежащая, то и в целом график симметричен относительно вертикальной оси.

Теперь посмотрим на степенные ф-ции, у которых нечетный показатель степени. В качестве примера можно привести у = х3 и у = х5. Видно, что они симметричны относительно центра координат:

Такая симметрия (относительно точки), называется центральной. Геометрически она означает, каждой точке графика в I четверти с двумя положительными координатами соответствует точка графика в III четверти с такими же координатами, но взятыми со знаком «минус»:

Существует множество ф-ций, обладающих подобной симметрией. В математике их все называют нечетными функциями. У них противоположным значениям аргументов соответствуют противоположные значения ф-ции, а график нечетной функции всегда симметричен относительно начала координат.

Чаще используется определение, содержащее формулу:

Покажем это свойство у ф-ции у = х3:

у(1) = 13 = 1 и у(– 1) = (– 1)3 = – 1;
у(2) = 23 = 8 и у(– 2) = (– 2)3 = – 8;
у(3) = 33 = 27 и у(– 3) = (– 3)3 = – 27.

Для того, чтобы доказать нечетность ф-ции, надо поставить в нее (– х) вместо х. Если получилась исходная ф-ция с противоположным знаком, то это значит, что ф-ция нечетная.

Пример. Докажите, что ф-ция у = х5 + х – нечетная.

Решение: Подставим (– х):

у(– х) = (– х)5 + (– х) = –х5 – х = – (х5 + х) = – у(х)

Получили исходную ф-цию, но со знаком «минус», поэтому ф-ция является нечетной.

Пример. Докажите нечетность ф-ции у = 5/х + 4х.

Решение. Подставляем в ф-цию (– х):

у = 5/(– х) + 4(– х) = – 5/х – 4х = – (5/х + 4х) = – у(х)

Снова получили исходную ф-цию со знаком минус, следовательно, мы исследовали нечетную ф-цию.

Известно, что любое целое число либо четное, либо нечетное. Однако с ф-циями всё по-другому. Существует множество ф-ций, которые не относятся ни к тем, ни к другим. Чтобы доказать, что ф-ция не является ни четной, ни нечетной, достаточно продемонстрировать, что хотя бы для одного значения х не выполняются условия у(– х) = у(х) и у(– х) = – у(х).

Пример. Докажите, что у = х3 + х2 – ни четная, ни нечетная ф-ция.

Решение. Определим значение ф-ции при, например, х = 1 и х = –1

у(1) = 13 + 12 = 2

у(– 1) = (– 1)3 + (– 1)2 = 0

Получили, что при противоположных х значения у не являются ни одинаковыми, ни противоположными. Значит, рассматриваемая ф-ция не подходит под приведенные определения четности и нечетности.

Мы сделали подборку лучших онлайн-курсов для эффективной подготовки к ОГЭ

Алгоритм определения

Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:

Записать функцию.
Подставить у или f(x)=0.
Решить получившееся уравнение.

Сложность последнего пункта зависит от степени аргумента уравнения

При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней

Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.

Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.

Уравнение у=х 2 -16 имеет два корня, и оба лежат в комплексной плоскости: х 1 =4і, х 2 =-4і.

Графическое представление

Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.

Свойства монотонных функций

Монотонные функции имеют ряд примечательных свойств, которые могут помогать при решении задач. Вспомним, что некоторые ф-ции могут при различных значениях аргументов принимать одинаковое значение. Например, таковой является степенная ф-ция у = х2:

у(2) = 4

у(– 2) = 4

С точки зрения графиков это означает, что горизонтальная линия может пересекать график ф-ции в нескольких точках:

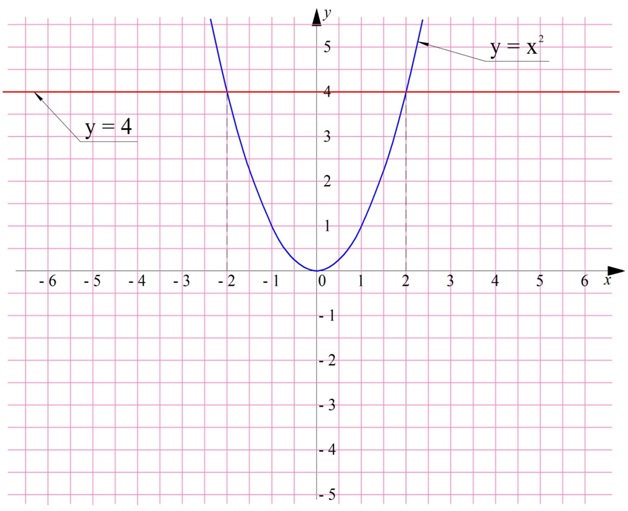
С другой стороны, это значит, что уравнение х2 = 4 имеет два корня, 2 и ( – 2).

Если же ф-ция строго монотонна, то такая ситуация невозможна. Любое ее значение может быть получено только при одном значении аргумента.

Действительно, если ф-ция монотонна, то любая горизонтальная прямая сможет пересечь ее график не более чем в одной точке:

Это также означает, что, если у(х) – строго монотонная ф-ция, а b– произвольное число, то уравнение у(х) = b имеет не более одного корня. Так, у уравнения х3 = 8 есть только один корень (он равен 2), потому что х3 – монотонная ф-ция.

Рассмотрим следующее свойство монотонных функций.

Действительно, ранее мы уже изучали сжатие и растягивание графиков. умножение ф-ции на постоянное число как раз и ведет к подобным преобразованиям. Ясно, что при этом не происходит изменение монотонности ф-ций:

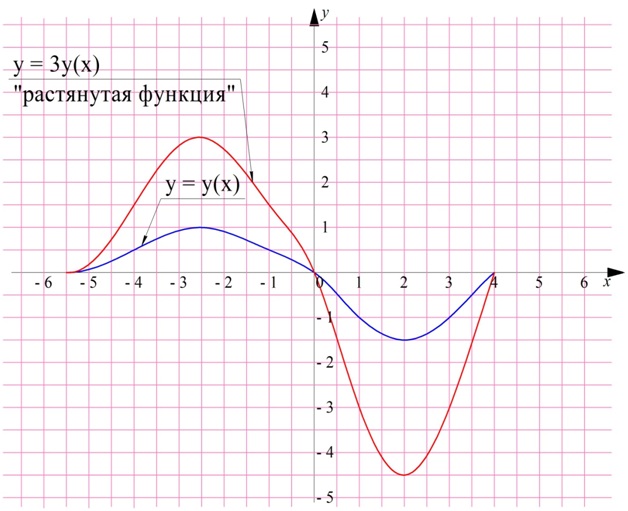
Например, парабола у = х2 возрастает на промежутке [0; + ∞), значит, и ф-ция у = 3х2 также возрастает на этом же промежутке:

Проще говоря, при умножении ф-ции на положительное число ее промежутки монотонности не изменяются.

А что же произойдет при умножении ф-ции на отрицательное число. Она не только сожмется или растянется, но ещё и отобразится симметрично относительно оси Ох. В результате промежутки возрастания ф-ции превратятся в промежутки убывания, и наоборот.

Проиллюстрируем это на примере ф-ций у = х2 и у = – х2:

Видно, что на промежутке (– ∞; 0] ф-ция у = – х2 возрастает, в то время как обычная парабола убывает.На промежутке [0; + ∞)ситуация противоположная.

Если две ф-ции одновременно возрастают на одном промежутке, то и их сумма также будет возрастать на этом промежутке.

Например, ф-ции у = х5 и у = 4х возрастают на всей числовой прямой. Следовательно, возрастающей является и ф-ция у = х5 + 4х.

Пример. Решите уравнение

х7 + 2х – 3 = 0

Решение. Можно заметить, что число 1 является корнем этого уравнения. Действительно, подставим единицу в уравнение и получим верное равенство:

17 + 2•1 – 3 = 0

1 + 2 – 3 = 0

0 = 0

Докажем, что других корней уравнение не имеет. В его левой части стоит сумма двух возрастающих ф-ций, у = х7 и у = 2х – 3. Следовательно, и ф-ция у = х7 + 2х – 3 также является возрастающей на всей числовой прямой. Это значит, что исследуемое уравнение имеет не более 1 корня, то есть корень х = 1 – единственный.

Ответ: 1.

Пример. Докажите, что у уравнения

не более одного корня.

Решение.

Выражение в левой части имеет смысл только при положительных х. Ведь если х < 0, то под корнем окажется отрицательное число, а если х = 0, то ноль окажется в знаменателе. Другими словами, уравнение имеет смысл на промежутке (0; + ∞). При этом левая часть представляет собой сумму трех слагаемых:

Первое и третье из них являются возрастающими ф-циями. Второе слагаемое – это взятая со знаком «минус» ф-ция у = 2/х. Так как у = 2/х убывает на промежутке (0; + ∞), то у = – 2/х на нем же возрастает. В итоге получаем, что в левой части сумма трех возрастающих ф-ций, значит, и всё это выражение – возрастающая ф-ция. Из этого следует, что у уравнения есть не более одного корня. Попробуйте сами подобрать его.

Алгоритм определения

Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:

Записать функцию.
Подставить у или f(x)=0.
Решить получившееся уравнение.

Сложность последнего пункта зависит от степени аргумента уравнения

Уравнение у=х2-16 имеет два корня, и оба лежат в комплексной плоскости: х₁=4і, х₂=-4і.

Примеры

Рассмотрим несложное уравнение у=х+3. Поскольку нуль функции — это значение аргумента, при котором у приобрел нулевое значение, подставим 0 в левую часть уравнения:

0=х+3;

х=-3.

В данном случае -3 и есть искомый нуль. Для данной функции существует только один корень уравнения, но так бывает далеко не всегда.

Рассмотрим другой пример:

у=х2-9.

Подставим 0 в левую часть уравнения, как и в предыдущем примере:

0=х2-9;

-9=х2 .

Очевидно, что в данном случае нулей функции будет два: х=3 и х=-3. Если бы в уравнении был аргумент третьей степени, нулей было бы три. Можно сделать простой вывод, что количество корней многочлена соответствует максимальной степени агрумента в уравнении. Однако многие функции, например у=х3 , на первый взгляд противоречат этому утверждению. Логика и здравый смысл подсказывают, что у этой функции только один нуль — в точке х=0. Но на самом деле корней три, просто все они совпадают. Если решать уравнение в комплексной форме, это становится очевидным. х=0 в данном случае, корень, кратность которого 3. В предыдущем примере нули не совпадали, потому имели кратность 1.

Ограниченные и неограниченные функции

Ещё раз рассмотрим ф-цию у = х2. Очевидно, что все точки ее графика лежат выше оси Ох (кроме точки (0;0), лежащей непосредственно на оси Ох). Ось Ох – это, по сути, горизонтальная прямая у = 0. Можно провести ряд других горизонтальных линий, каждая из которых лежит ниже параболы и не пересекает её:

В математике говорят, что ф-ция у = х2 ограничена снизу. То есть для любого допустимого х выполняется неравенство у(х) ⩾ а, где а – это какое-то произвольное число. И действительно, неравенство х2⩾ 0 выполняется при всех значениях х. Также выполняются неравенства

х2⩾ – 1,5

х2⩾ – 3

х2⩾ – 5

Дадим определение функции, ограниченной снизу

Очевидно, что если неравенство у(х) ⩾ а выполняется хотя бы для одного числа а, то оно выполняется и для всех а, которые ещё меньше. Так, из справедливости неравенства х2⩾ 0 автоматически следует справедливость неравенства х2⩾ – 1,5, так как

– 1,5 ⩽ 0.

Аналогично в математике существует понятие функции, ограниченной сверху.

В качестве примера ограниченной сверху ф-ции можно привести у = 4 – х2:

Ясно, что неравенство 4 – х2⩽ 4 выполняется при всех х, то есть ни одна точка графика не лежит выше прямой у = 4.

Иногда бывает так, что функция ограничена одновременно и снизу, и сверху. Их называют ограниченными функциями.

Ф-ция, не попадающее под это определение, называется неограниченной функцией. В качестве примера неограниченной функции можно привести линейную ф-цию у = х + 1.

График ограниченной ф-ции находится в своеобразной «полосе» из горизонтальных линий, которые ограничивают его сверху и снизу. Примером ограниченной ф-ции является

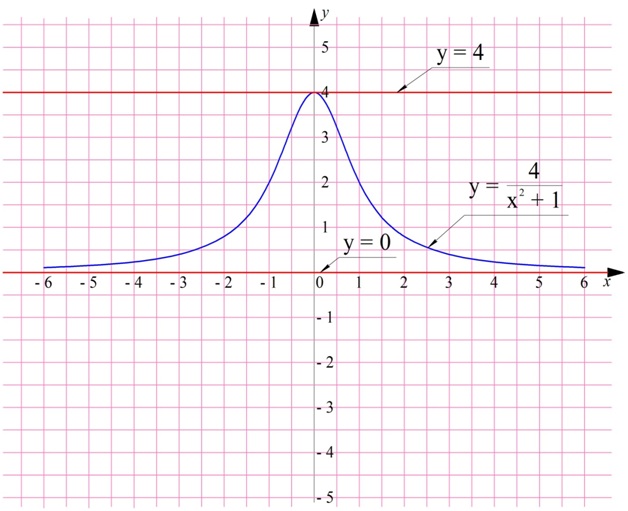
С одной стороны, у этой дроби и числитель, и знаменатель – положительное число, поэтому она ограничена снизу прямой у = 0. С другой стороны, дробь тем больше, чем меньше ее знаменатель (если они оба положительны). Минимальное значение выражения х2 + 1 – это единица (при х = 0), а поэтому максимальное значение дроби равно 4/1 = 4. Поэтому график ограничен сверху прямой у = 4.

Пример. Ограничена ли ф-ция

Решение. Выделим в ф-ции целую часть:

Так как величина 5х2 + 5 всегда положительна, то и дробь

а значит, и вообще вся ф-ция положительна, то есть ограничена снизу прямой у = 0

С другой стороны, дробь будет принимать максимальное значение при минимальном значении знаменателя, которое равно 5 (при х = 0) При х = 0 имеем

Получается, что ф-ция ограничена сверху прямой у = 1,4.

Ответ: ограничена.

Пример. Ограничена ли ф-ция

Решение. Величина х2 всегда положительна, то есть х2⩾ 0. Преобразуем это неравенство, умножив его на (– 1) и добавив к нему 16:

х2⩾ 0

– х2⩽ 0

16 – х2⩽ 16

Получили, что подкоренное выражение не превосходит 16, а значит, и корень из него не больше, чем

То есть график будет ограничен прямой у = 4 сверху. С другой стороны, арифметический квадратный корень не может быть отрицательным числом, а потому его график ограничен снизу прямой у = 0. Для наглядности покажем график исследуемой ф-ции:

Ответ: ограничена.

Промежутки монотонности основных функций

Мы ранее уже изучили несколько видов ф-ций. Посмотрим, какие у них промежутки монотонности.

Поведение линейной ф-ции у = kх + b зависит исключительно от значение коэффициента k. Если он больше нуля, то функция возрастает на промежутке (– ∞; + ∞), то есть на всей числовой прямой. Если же k< 0, то ф-ция будет убывать. Если k = 0, то график будет выглядеть как горизонтальная линия. Её можно считать одновременно и неубывающей, и невозрастающей ф-цией. Приведем примеры на рисунке:

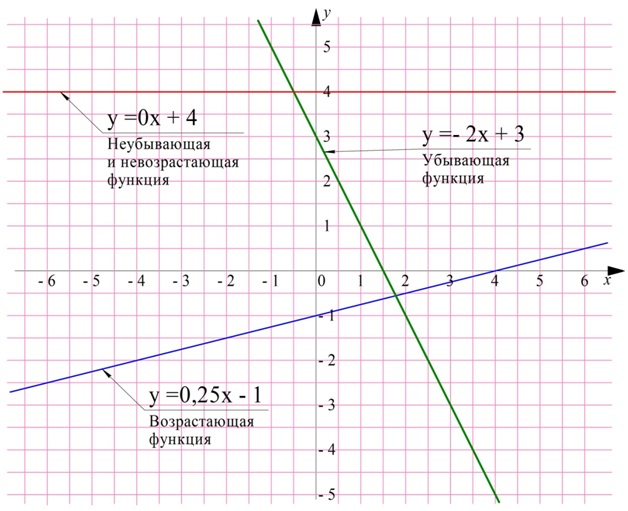
Поведение обратной пропорциональности у = k/х также зависит от значения k. Если он больше нуля, то ф-ция убывает на двух промежутках: (– ∞;0) и (0; + ∞).

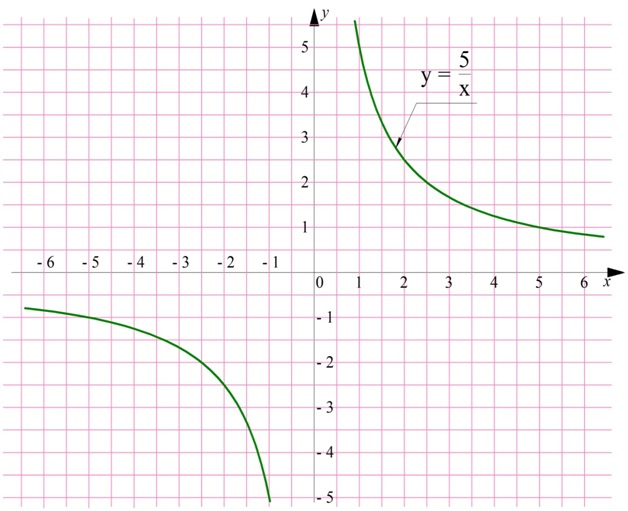
Здесь стоит обратить внимание, что, хотя у ф-ции нет ни одного участка, на котором бы она возрастала, нельзя утверждать, что обратная пропорциональность убывает на всей своей области определения (– ∞; 0)∪(0; + ∞). Например, сравним значение ф-ции у = 5/х при х1 = – 1 и х2 = 1:. у(– 1) = 5/(– 1) = – 5

у(– 1) = 5/(– 1) = – 5

у(1) = 5/1 = 5

Получили, что для этих значений х₁<x₂, а у(– 1) <у(1), поэтому ф-цию нельзя считать убывающей на всей области определения.

Если в обратной пропорциональности коэффициент k отрицательный, то ф-ция возрастает на промежутках (– ∞;0) и (0; + ∞):

Ф-ция

возрастает на всей своей области определения, то есть на промежутке [0; + ∞):

Поведение степенной ф-ции у = хn зависит от показателя n. Если он нечетный, то получается ф-ция, возрастающая на всей числовой прямой:

Если же число n четное, то степенная ф-ция будет убывать на промежутке (– ∞:0] и возрастать на промежутке [0; + ∞):

Пример. Найдите значения параметра a, при котором ф-ция

у = (5а – 2)х +16

является возрастающей.

Решение. Данная ф-ция является линейной ф-цией вида у = kx + b, где в роли коэффициента k выступает выражение (5а – 2). Ф-ция будет возрастать, если этот коэффициент будет больше нуля, то есть

5а – 2> 0

5а> 2

а > 0,4

Получаем, что ф-ция будет возрастающей при значениях а, больших 0,4, или, другими словами, при а∊(4; + ∞).

Ответ: а∊(4; + ∞).

Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы