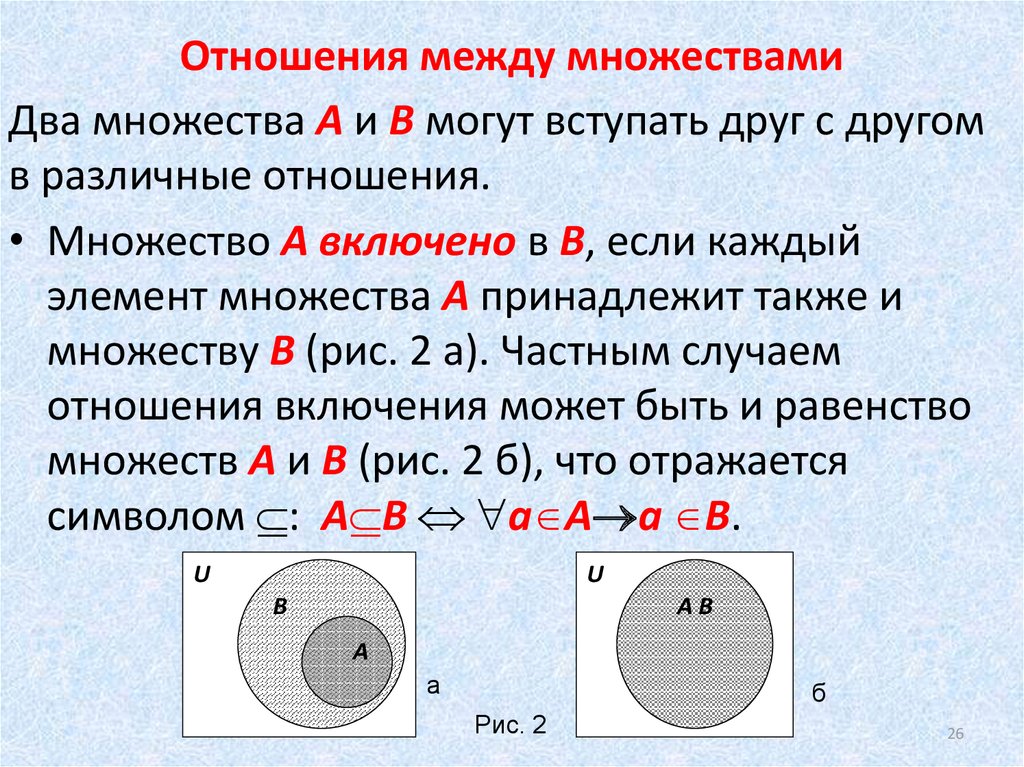
Множества: понятие, определение, примеры

Отображение множеств

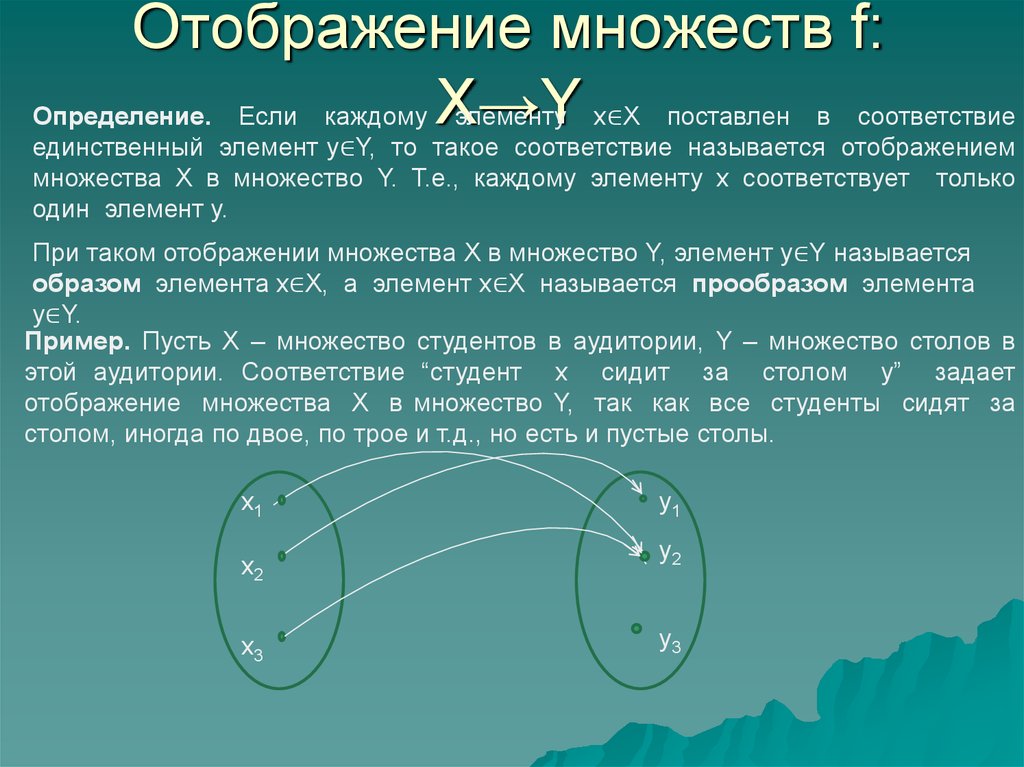
Отображение множества во множество – это правило, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой – она ставит в соответствие каждому элементу единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

Векторы Матрицы Определители Комплексные числа (о, да!) Теория пределов Что такое производная?

Установленное (добровольно или принудительно =)) правило ставит в соответствие каждому студенту множества единственную тему реферата множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества образуют область определения функции (обозначается через ), а элементы множества – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена – одна из тем останется невостребованной.

Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)

Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции .

Задумаемся, что это такое? Это правило , которое каждому элементу области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение . С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:

Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).

Далее взглянем на старую знакомую параболу . Здесь правило каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:

Итак, что же такое функция одной переменной? Функция одной переменной – это правило , которое каждому значению независимой переменной из области определения ставит в соответствие одно и только одно значение .

Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции каждому «иксу» области определения соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.

! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример:

А вот у квадратичной функции не наблюдается ничего подобного, во-первых: – то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

Действия над множествами. Диаграммы Венна

Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:

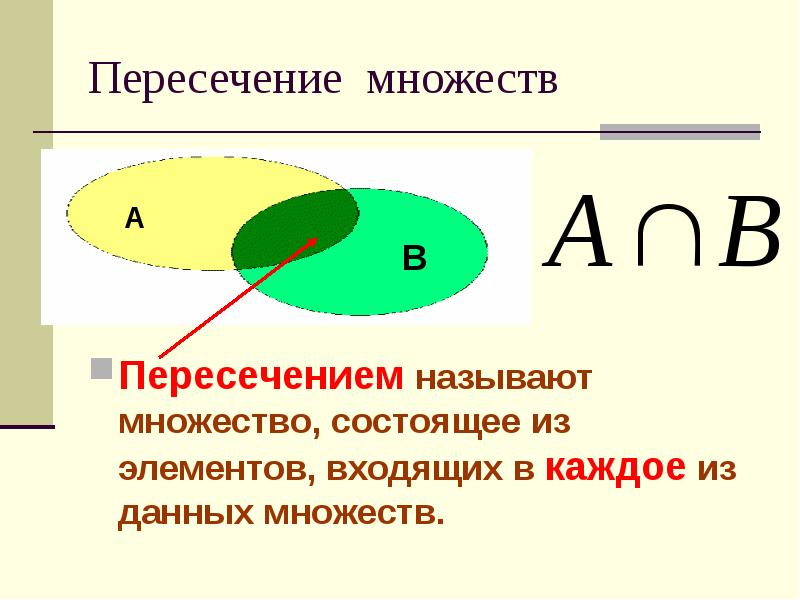
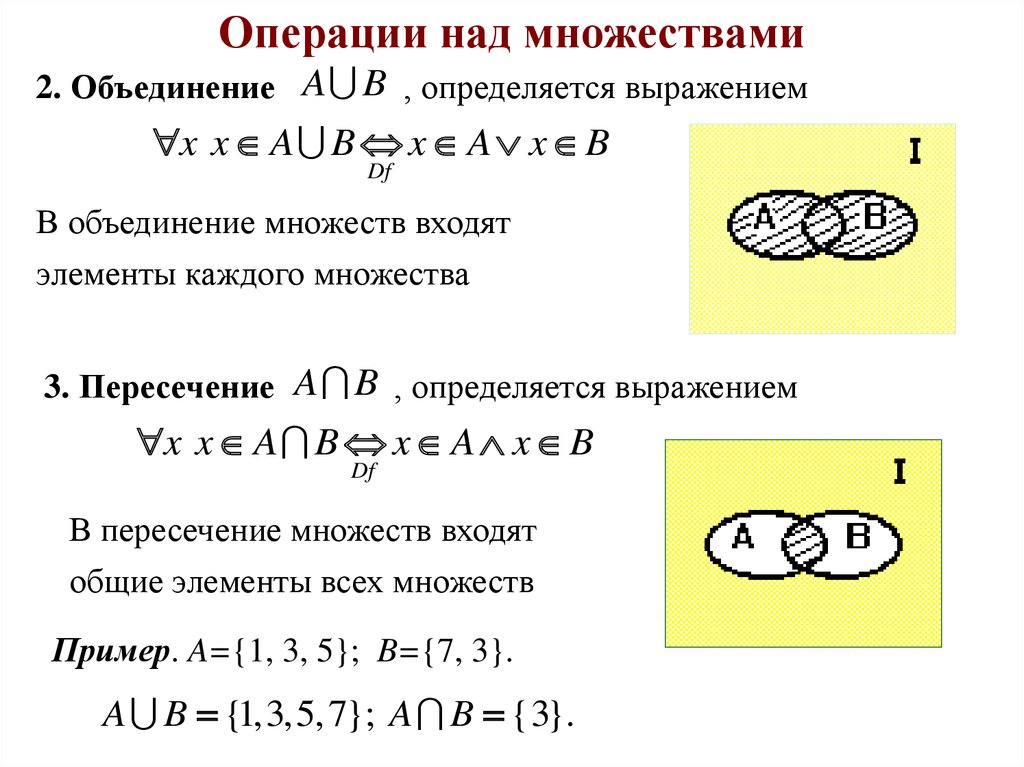
1) Пересечение множеств характеризуется логической связкой И и обозначается значком

Пересечением множеств и называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:
Так, например, для множеств :

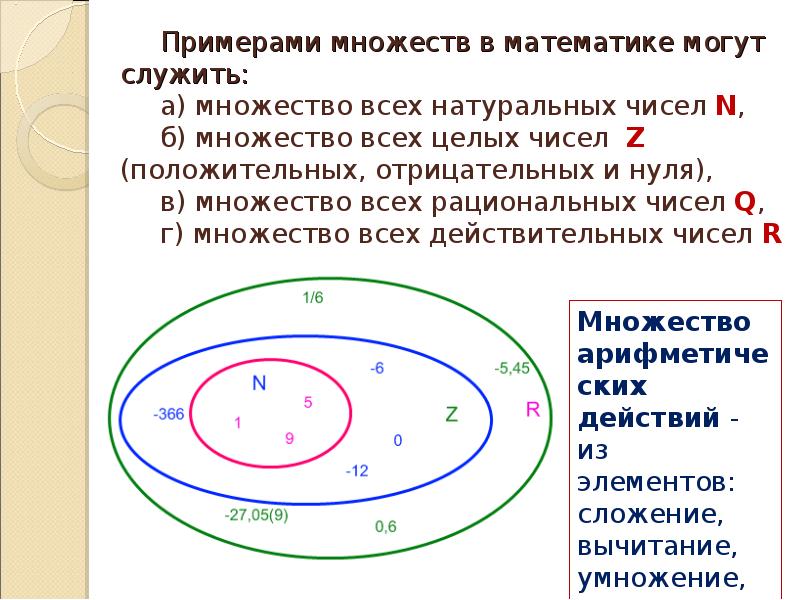
Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:

Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.

Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший .

2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком

Объединением множеств и называется множество , каждый элемент которого принадлежит множеству или множеству :

Запишем объединение множеств : – грубо говоря, тут нужно перечислить все элементы множеств и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.

Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:

В этом случае можно изобразить два непересекающихся заштрихованных круга.

Операция объединения применима и для бОльшего количества множеств, например, если , то:

, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:

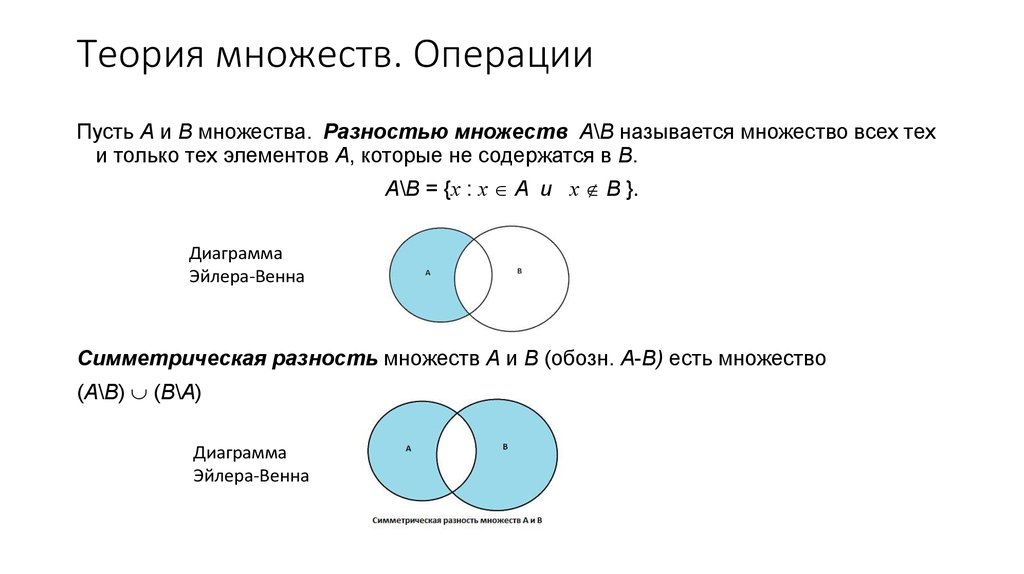
3) Разностью множеств и называют множество , каждый элемент которого принадлежит множеству и не принадлежит множеству :
Разность читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества . Чтобы записать разность , нужно из множества «выбросить» все элементы, которые есть во множестве :

Пример с числовыми множествами: – здесь из множества целых чисел исключены все натуральные, да и сама запись так и читается: «множество целых чисел без множества натуральных».

Зеркально: разностью множеств и называют множество , каждый элемент которого принадлежит множеству и не принадлежит множеству :
Для тех же множеств – из множества «выброшено» то, что есть во множестве .

А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется 🙂

Кроме того, иногда рассматривают симметрическую разность , которая объединяет оба «полумесяца»: – иными словами, это «всё, кроме пересечения множеств».

4) Декартовым (прямым) произведением множеств и называется множество всех упорядоченных пар , в которых элемент , а элемент

Запишем декартово произведение множеств :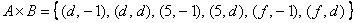 – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества последовательно присоединяем каждый элемент множества , затем ко 2-му элементу множества присоединяем каждый элемент множества , затем к 3-му элементу множества присоединяем каждый элемент множества »: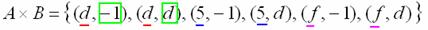

Зеркально: декартовым произведением множеств и называется множество всех упорядоченных пар , в которых . В нашем примере: – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы: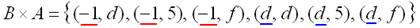

Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары. А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат

А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат .

Задание для самостоятельного закрепления материала:

Выполнить операции , если:

1) ;
2)

Множество удобно расписать перечислением его элементов.

И пунктик с промежутками действительных чисел:

Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству , а «тройка» не принадлежит множеству . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если возникнут затруднения, выполните чертёж 😉

Краткое решение задачи в конце урока.

Операции над множествами

Диаграмма Венна для A∩B{\displaystyle A\cap B}
Диаграмма Венна для A∪B{\displaystyle A\cup B}
Диаграмма Венна для A∖B{\displaystyle A\setminus B}
Диаграмма Венна для A△B{\displaystyle A\triangle B}

Бинарные операции

Основные бинарные операции, определяемые над множествами:

пересечение:

A∩B:={x∣x∈A∧x∈B}{\displaystyle A\cap B:=\{x\mid x\in A\land x\in B\}}.
объединение:

A∪B:={x∣x∈A∨x∈B}{\displaystyle A\cup B:=\{x\mid x\in A\lor x\in B\}}.

Если множества A{\displaystyle A} и B{\displaystyle B} не пересекаются, то A∩B=∅{\displaystyle A\cap B=\varnothing }. Их объединение обозначают также: A+B=A∪B{\displaystyle A+B=A\cup B}.

разность:

A∖B:=A∩B¯={x∣x∈A∧x∉B}{\displaystyle A\setminus B:=A\cap {\overline {B}}=\{x\mid x\in A\land x\notin B\}}.
симметрическая разность:

A△B≡A−˙B:={\displaystyle A\bigtriangleup B\equiv A\;\;\!\!{\dot {-}}\;\;\!\!B:=}

(A∪B)∖(A∩B)=A∩B¯+A¯∩B={\displaystyle (A\cup B)\setminus (A\cap B)=A\cap {\overline {B}}+{\overline {A}}\cap B=}

={x∣(x∈A∧x∉B)∨(x∉A∧x∈B)}{\displaystyle =\{x\mid (x\in A\land x\notin B)\lor (x\notin A\land x\in B)\}}.
декартово или прямое произведение:

A×B={(a,b)∣a∈A,b∈B}{\displaystyle A\times B=\{(a,\;b)\mid a\in A,\;b\in B\}}.

Для объяснения смысла операций часто используются диаграммы Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.

Всякая система множеств, замкнутая относительно операций объединения и пересечения, образует относительно объединения и пересечения дистрибутивную решётку.

Унарные операции

Диаграмма Венна для (A∩B)∁{\displaystyle (A\cap B)^{\complement }}

Дополнение определяется следующим образом:

A¯≡A∁:={x∣x∉A}{\displaystyle {\overline {A}}\equiv A^{\complement }:=\{x\mid x\notin A\}}.

Операция дополнения подразумевает некоторый зафиксированный универсум (универсальное множество U{\displaystyle U}, которое содержит A{\displaystyle A}), и сводится к разности множеств с этим универсумом:

A¯=U∖A{\displaystyle {\overline {A}}=U\setminus A}.

Система множеств с фиксированным универсумом, замкнутая относительно операций объединения, пересечения с введённым таким образом дополнением образует булеву алгебру.

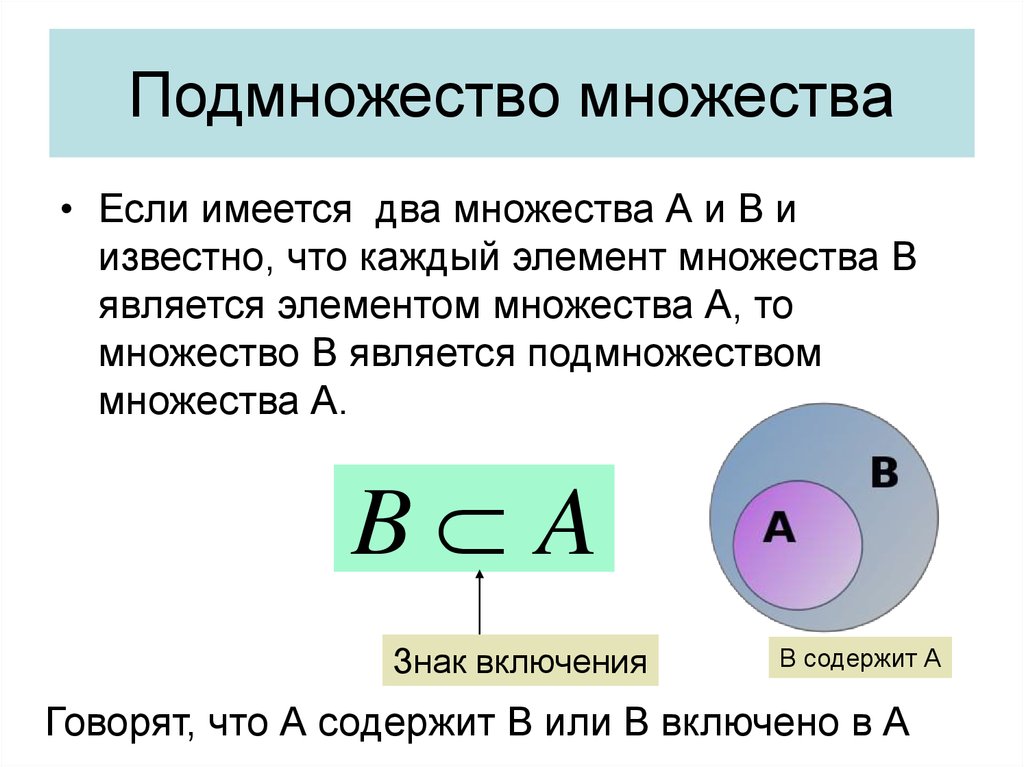
Булеан — множество всех подмножеств:

2X≡PX:={A∣A⊂X}{\displaystyle 2^{X}\equiv {\mathcal {P}}X:=\{A\mid A\subset X\}}.

Обозначение 2X{\displaystyle 2^{X}} происходит из свойства мощности множества всех подмножеств конечного множества:

|2X|=2|X|{\displaystyle \left|2^{X}\right|=2^{|X|}}.

Булеан 2X{\displaystyle 2^{X}} порождает систему множеств с фиксированным универсумом X{\displaystyle X}, замкнутую относительно операций объединения и пересечения, то есть, образует булеву алгебру.

Приоритет операций

Последовательность выполнения операций над множествами, как и обычно, может быть задана скобками. При отсутствии скобок сначала выполняются унарные операции (дополнение), затем — пересечения и разности, которые имеют одинаковый приоритет, затем — объединения и симметрической разности[источник не указан 326 дней]. Операции одного приоритета выполняются слева направо. При этом надо иметь в виду, что в отличие от арифметических сложения и вычитания, для которых верно, что (a+b)−c=a+(b−c){\displaystyle (a+b)-c=a+(b-c)}, для аналогичных операций над множествами это неверно. Например, если A={1,3},B={1,2},C={2,3},{\displaystyle A=\{1,3\},B=\{1,2\},C=\{2,3\},} то (A∪B)∖C={1},{\displaystyle (A\cup B)\setminus C=\{1\},} но, в то же время, A∪(B∖C)={1,3}{\displaystyle A\cup (B\setminus C)=\{1,3\}}.

Решение совокупностей неравенств

Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.

Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.

А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.

Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:

Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.

Решением первого неравенства x ≥ 3 является числовой промежуток .

Множество значений x, при которых верно хотя бы одно из неравенств, будет принадлежать промежутку . Так и записываем:

x ∈

В этом выражении говорится, что переменная x, входящая в
совокупность принимает все значения, принадлежащие промежутку . А это то, что нам нужно. Ведь решить совокупность означает найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность. А любое число из промежутка будет удовлетворять хотя бы одному неравенству.

Например, число 9 из промежутка удовлетворяет второму неравенству x ≤ 6.

Посмотрите внимательно на выражение x ∈ , а именно на его правую часть. Ведь выражение представляет собой объединение числовых промежутков . Точнее, объединение множеств решений первого и второго неравенства.

Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.

Иначе говоря, решением совокупности будет объединение числовых промежутков

Объединением числовых промежутков является промежуток (−∞; +∞). Точнее, объединением числовых промежутков является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть

= (−∞; +∞)

Ответ можно оставить таким, каким мы его записали ранее:

x ∈

либо заменить на более короткий:

x ∈ (−∞; +∞)

Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.

Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.

8 ≥ 3

Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6

1 ≤ 6

Возьмем еще какое-нибудь число, например, число 5. Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6

Пример 2. Решить совокупность неравенств

Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.

Для начала найдём множество решений первого неравенства x < −0,25. Этим множеством является числовой промежуток (−∞; −0,25).

Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).

Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.

x ∈ (−∞; −0,25) ∪ [−7; +∞)

Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −0,25) и [−7; +∞)

Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть

(−∞; −0,25) ∪ [−7; +∞) = (−∞; +∞)

Ответ можно оставить таким, каким мы его записали ранее:

x ∈ (−∞; −0,25) ∪ [−7; +∞)

либо заменить на более короткий:

x ∈ (−∞; +∞)

Пример 3. Решить совокупность неравенств

Решим каждое неравенство по отдельности:

Множеством решений первого неравенства x < −3 является числовой промежуток (−∞; −3).

Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0].

Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.

x ∈ (−∞; −3) ∪ (−∞; 0]

Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −3) и (−∞; 0]

Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]

(−∞; −3) ∪ (−∞; 0] = (−∞; 0]

Ответ можно оставить таким, каким мы его записали ранее:

x ∈ (−∞; −3) ∪ (−∞; 0]

либо заменить на более короткий:

x ∈ (−∞; 0]

Задание множества

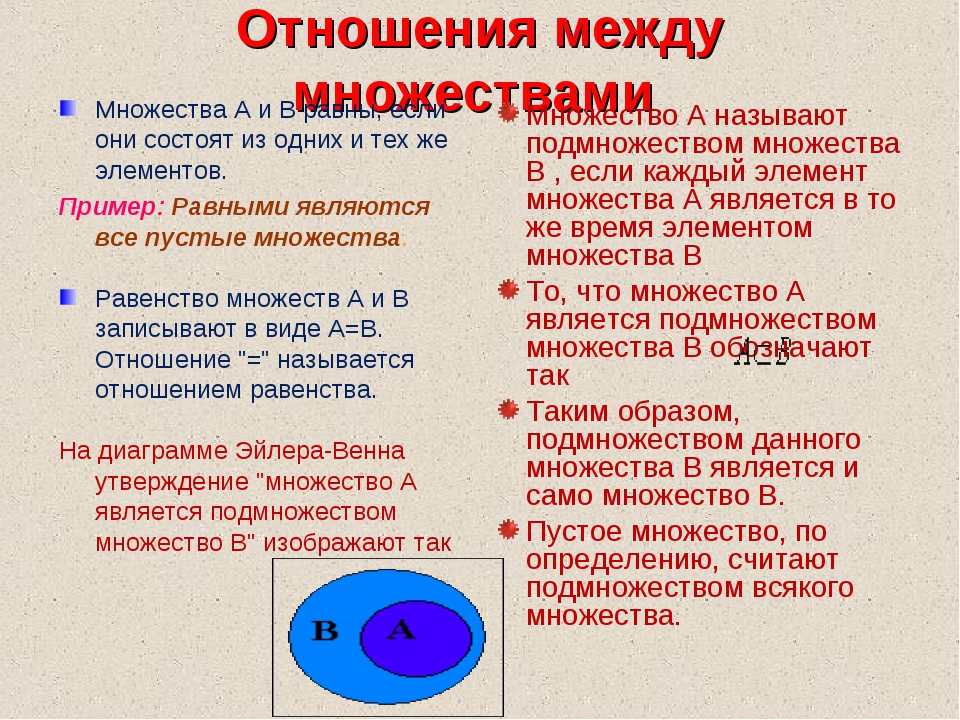
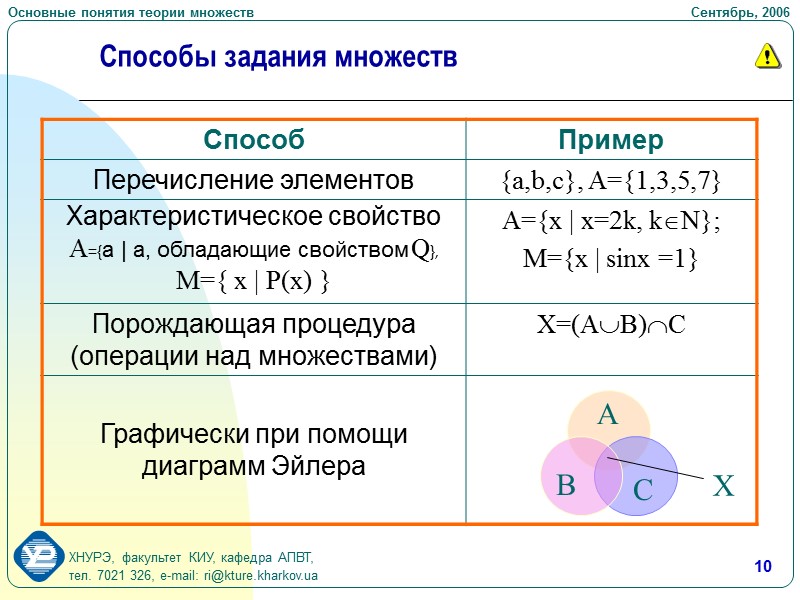
Существуют два основных способа задания множеств: перечисление и описание.

Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество Y{\displaystyle Y} неотрицательных чётных чисел, меньших 10 можно задать в виде списка: Y={,2,4,6,8}{\displaystyle Y=\left\{0,2,4,6,8\right\}}. Данный способ удобно применять лишь к ограниченному числу конечных множеств.

Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка. В таком случае множества определяются свойствами их элементов. Множество Y{\displaystyle Y} задано, если указано условие A(x){\displaystyle A(x)}, которому удовлетворяют все элементы, принадлежащие множеству Y{\displaystyle Y} и которому не удовлетворяют элементы, не принадлежащие множеству Y{\displaystyle Y}.

Обозначение

Y={x∈X∣A(x)},{\displaystyle Y=\{\,x\in X\mid A(x)\,\},}

используется для задания множества Y{\displaystyle Y}; оно означает, что множество Y{\displaystyle Y} состоит из тех и только тех элементов x{\displaystyle x} множества X{\displaystyle X}, для которых выполнено условие A(x){\displaystyle A(x)}.

Например, график функции fX→Y{\displaystyle f\colon X\to Y} можно задать следующим образом:

Γ={(x,y)∈X×Y∣f(x)=y},{\displaystyle \Gamma =\{\,(x,y)\in X\times Y\mid f(x)=y\,\},}

Множества мощности континуума

Если можно установить взаимно однозначное соответствие между элементами множества \(M\) и точками отрезка \(0\leqslant x\leqslant1\) , то говорят, что множество \(M\) имеет мощность континуума. В частности, согласно этому определению, само множество точек отрезка \(0\leqslant x\leqslant1\) имеет мощность континуума.

Из рис. 1 видно, что множество точек любого отрезка \(AB\) имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.

Нетрудно показать, что множества точек любого интервала \(x\in\) и всей числовой прямой \(x\in\) — имеют мощность континуума.

Значительно более интересен такой факт: множество точек квадрата \(0\leqslant x\leqslant1,\) \(0\leqslant y\leqslant1\) имеет мощность континуума. Таким образом, грубо говоря, в квадрате «столько же» точек, сколько и в отрезке.

Теория множествМножества Формулы Алгебра Теория

В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

История понятия

Основная статья: История теории множеств

Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.

С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством».
Эти объекты назвал элементами множества.
Множество объектов, обладающих свойством A(x){\displaystyle A(x)}, обозначил {x∣A(x)}{\displaystyle \{x\mid A(x)\}}.
Если некоторое множество Y={x∣A(x)}{\displaystyle Y=\{x\mid A(x)\}}, то A(x){\displaystyle A(x)} назвал характеристическим свойством множества Y{\displaystyle Y}.

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

Так как теория множеств фактически используется как основание и язык всех современных математических теорий, в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.

В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора).
При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами.
Такие совокупности называются классами (различных порядков).

История понятия

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.

Решение неравенств, содержащих знак ≠

Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8. Чтобы решить такое неравенство, нужно найти множество значений переменной x, при которых левая часть не равна правой части.

Решим неравенство 2x ≠ 8. Разделим обе части данного неравенства на 2, тогда получим:

Получили равносильное неравенство x ≠ 4. Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.

Подставим, например, число 5

5 ≠ 4 — верное неравенство, поскольку 5 не равно 4

Подставим 7

7 ≠ 4 — верное неравенство, поскольку 7 не равно 4

И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8, то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8. Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8.

2 × 5 ≠ 8

2 × 7 ≠ 8

Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:

Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪

x ∈ (−∞; 4) ∪ (4; +∞)

В этом выражении говорится, что значения, принимаемые переменной x, принадлежат промежутку (−∞; 4) или промежутку (4; +∞).

Неравенства, содержащие знак ≠, также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак =. Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.

Решим предыдущее неравенство 2x ≠ 8, как обычное уравнение. Заменим знак ≠ на знак равенства =, получим уравнение 2x = 8. Разделим обе части данного уравнения на 2, получим x = 4.

Видим, что при x, равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.

Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x

Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:

Приведем подобные слагаемые в обеих частях:

Разделим обе части получившегося неравенства на 5

Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2.

Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:

x ∈ (−∞; 1,2) ∪ (1,2; +∞)

В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)

Конечные и бесконечные множества

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.

Рассмотрим два каких-либо множества \(M\) и \(N\) и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.

Если множество \(M\) конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств \(M\) и \(N\) достаточно сосчитать число элементов в \(M\) , число элементов в \(N\) и сравнить полученные числа. Естественно также считать, что если одно из множеств \(M\) и \(N\) конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное.

Однако, если оба множества \(M\) и \(N\) бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.