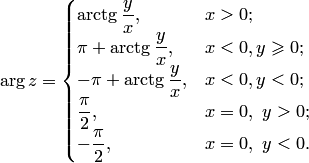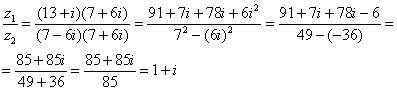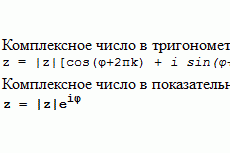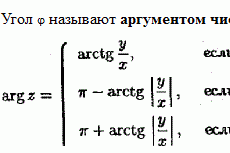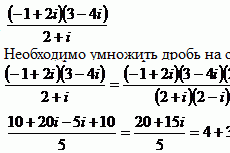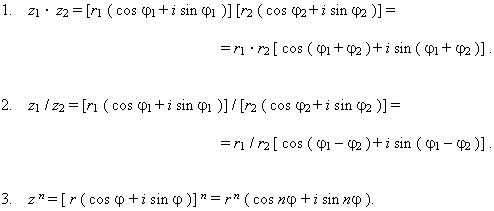Геометрическая интерпретация комплексного числа.
Комплексная плоскость.
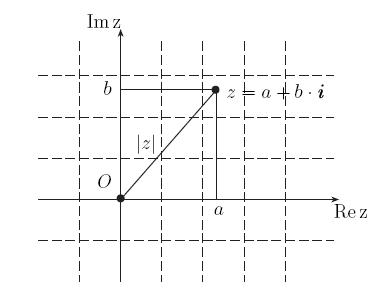
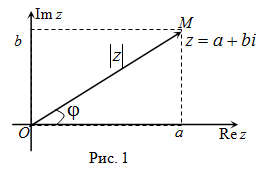
Пусть на плоскости задана прямоугольная система координат. Комплексное число \(z=x+iy\) изображается точкой плоскости с координатами \((x,y)\), и эта точка обозначается той же буквой \(z\).
Такое соответствие между множеством \(\mathbb{C}\) и точками плоскости является взаимно однозначным: каждому числу \(z\in\mathbb{C}\) соответствует одна точка плоскости с координатами \((x,y)\), и наоборот, каждой точке плоскости с координатами \((x,y)\) соответствует одно комплексное число \(z=x+iy\). Поэтому слова “комплексное число” и “точка плоскости” часто употребляются как синонимы.
При этом действительные числа, то есть числа вида \(x+0\cdot i\), изображаются точками оси абсцисс, а чисто мнимые числа, то есть числа вида \(iy = 0 + iy\) — точками оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат — мнимой осью. Плоскость, на которой изображаются комплексные числа, называют комплексной плоскостью.
Рис. 31.1
На рис. 31.1 изображены точки \(z,\ -z,\ \overline{z},\ -\overline{z}\). Отметим, что точки \(z\) и \(-z\) симметричны относительно точки \(O\), а точки \(z\) и \(\overline{z}\) симметричны относительно действительной оси.
Геометрический смысл модуля комплексного числа.
Комплексное число \(z=x+iy\) можно изображать вектором с началом в точке \(O\) и концом в точке \(z\). Этот вектор будем обозначать той же буквой \(z\). Из рис. 31.1 или из формулы \eqref{ref4} видно, что длина вектора \(z\) равна \(|z|\) и справедливы неравенства \(|x|\leq |z|,\ |y|\leq |z|\), то есть
$$
|Re\ z|\leq |z|,\quad |Im\ z|\leq |z|.\nonumber
$$
Рис. 31.2Рис. 31.3
С помощью векторной интерпретации наглядно иллюстрируются сумма и разность комплексных чисел. Число \(z_1+z_2\) изображается вектором, построенным по правилу сложения векторов \(z_1\) и \(z_2\), а вектор \(z_1-z_2\) можно построить как сумму векторов \(z_1\) и \(-z_2\). Из рис. 31.2 видно, что расстояние между точками \(z_1\) и \(z_2\) равно длине вектора \(z_1-z_2\), то есть равно \(|z_1-z_2|\). Это же утверждение следует из равенства
$$
|z_1-z_2|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}.\nonumber
$$
Итак, \(|z_1-z_2|\) — расстояние между точками \(z_1\) и \(z_2\).
Пример 2.
Дать геометрическое описание множества всех точек комплексной плоскости, удовлетворяющих условию:
- \(|z-z_0| = R,\ R > 0\);
- \(1 < |z-1| < 2\);
- \(|z-i| = |z + i|\).
- \(\triangle\) Условию \(z-z_0=R\), где \(R > 0\), \(z_0\) — заданное комплексное число, удовлетворяют все точки, расстояние от которых до точки \(z_0\) равно \(R\), то есть точки, лежащие на окружности радиуса \(R\) с центром в точке \(z_0\).
- Условию \(|z-1| < 2\) удовлетворяют все точки, лежащие внутри круга радиуса 2 с центром в точке \(z = 1\), а условию \(|z-1| > 1\) — точки, лежащие вне круга радиуса 1 с центром в точке \(z = 1\).
Оба эти условия выполняются для точек, лежащих между окружностями \(|z-1| = 1\) и \(|z-1| = 2\) (рис. 31.3). - Условию \(|z-i| = |z + i|\) удовлетворяют те и только те точки, которые равноудалены от точек \(i\) и \(-i\), то есть все точки действительной оси. \(\blacktriangle\)
Покажем, что для любых комплексных чисел \(z_1\) и \(z_2\) справедливы неравенства
$$
||z_1|-|z_2||\leq |z_1+z_2|\leq |z_1|+|z_2|.\label{ref10}
$$
\(\circ\) Рассмотрим треугольник с вершинами \(0,\ z_1\) и \(z_1+z_2\) (рис. 31.2). Длины его сторон равны \(|z_1|,\ |z_2|\) и \(|z_1+z_2|\). Поэтому неравенства \eqref{ref10} выражают известные из геометрии свойства длин сторон треугольника. \(\bullet\)
[править] Литература
|
Числовые системы |
|
|---|---|
|
множества |
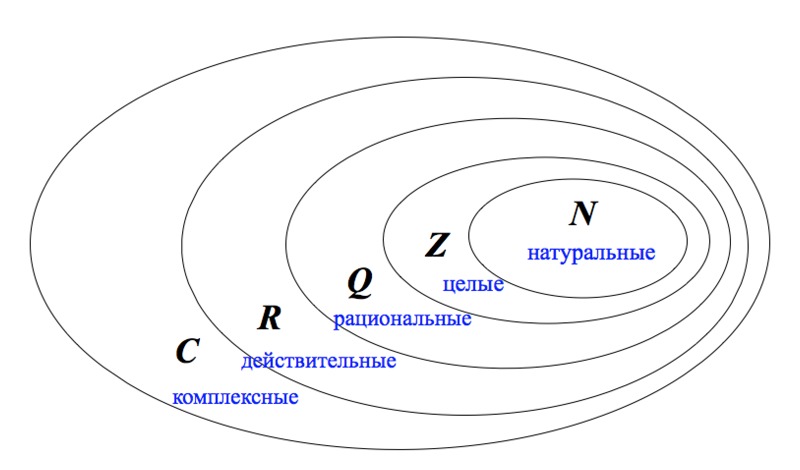
Натуральные числа (\scriptstyle\mathbb{N}) • Целые (\scriptstyle\mathbb{Z}) • Рациональные (\scriptstyle\mathbb{Q}) • Алгебраические (\scriptstyle\overline{\mathbb{Q}}) • Периоды • Вычислимые |
|
и их расширения |
Действительные (вещественные) (\scriptstyle\mathbb{R}) • Комплексные (\scriptstyle\mathbb{C}) • Кватернионы (\scriptstyle\mathbb{H}) • Числа Кэли (октавы, октонионы) (\scriptstyle\mathbb{O}) • Седенионы (\scriptstyle\mathbb{S}) • Альтернионы • Дуальные • Гиперкомплексные • Супердействительные • Гипервещественные • Сюрреальные |
|
числовые системы |
Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
|
|
Двойные числа • Иррациональные числа • Трансцендентные числа • Числовой луч • Бикватернионы • Координатизация • Расширение понятия числа |
Реальный пример: Вращения
Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:
Умножение на комплексное число совершает вращение на его угол
Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?
Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…
Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ)
Так что мы можем умножить наш курс на это число!
Вот в чем суть:
- Исходный курс: 3 единицы на Восток, 4 единицы на Север = 3 + 4i
- Вращение против часовой стрелки на 45 градусов = умножение на 1 + i
При умножении мы получаем:
Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.
Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!
Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?
Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!
Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!
Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.
Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»
Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.
А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.
Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
С алгебраической формой комплексного числа мы уже познакомились, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.
Сложение комплексных чисел
Пример 1
Сложить два комплексных числа ,
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел и , если ,
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .
Рассчитаем вторую разность:
Здесь действительная часть тоже составная:
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел ,
Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
Надеюсь, всем было понятно, что
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4
Даны комплексные числа , . Найти частное .
Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть
Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).
Распишу подробно:
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:
Редко, но встречается такое задание:
Пример 5
Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).
Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :
Пример 6
Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что
По каким критериям выбирать брокера бинарных опционов?
На данный момент, бинарные опционы один из самых эффективных средств заработка. Прибыль может быть равна полной стоимости ставки, а стремительная торговля позволяет вводить в оборот достаточно крупные суммы. Для доступа к терминалу требуются услуги проверенных брокерских контор, которые полностью удовлетворят запросы трейдера.

Именно от верно выбранного брокера во многом зависит успешная торговля. Это сложная и ответственная задача, которую лучше решать со спокойной головой. На сегодня рынок представляет различные брокерские конторы, которые подойдут как новичкам, так и опытным трейдерам.
Именно поэтому аналитики предоставляют доступ к рейтингам брокеров бинарных опционов, где учитывается огромный список параметров.
Для того, чтобы брокеру лидировать в топе, он должен соответствовать следующим критериям:
- срок успешной работы на рынке – более 2 лет;
- количество довольных клиентов;
- эффективная техническая поддержка;
- быстрый и простой ввод и вывод средств;
- положительная характеристика и отсутствие претензий у регулирующих брокерскую деятельность инстанций;
- величина ставок и депозитов;
- развитие инструментария, увеличение оборотов;
- бонусная система;
- прозрачная статистика и аналитика;
- широкий спектр торговых активов;
- возможность обучения и наличие демо-счетов;
- отсутствие блокировки аккаунтов;
- отсутствие уменьшения выплат в случае стабильной успешной торговли;
- возможность участия в семинарах и других обучающих программах.
На данный момент лидерами брокеров в сфере бинарной торговли являются: Binomo, Olymptrade, Binary, 24Option, Finmax и другие. Каждый может самостоятельно посмотреть статистику и сделать оптимальный выбор.
ТОП БРОКЕРОВ, ПРИЗНАННЫХ НЕЗАВИСИМЫМИ РЕЙТИНГАМИ
*БО. Не требуется верификация! | обзор/отзывы | НАЧАТЬ ТОРГОВЛЮ С 10$
 *БО. Выплаты до 218% за сделку! | обзор/отзывы | НАЧАТЬ С 10 $
*БО. Выплаты до 218% за сделку! | обзор/отзывы | НАЧАТЬ С 10 $
ЛУЧШИЕ ФОРЕКС БРОКЕРЫ ПО ДАННЫМ «ИНТЕРФАКС»
2007 год. FinaCom. КОПИРОВАТЬ СДЕЛКИ ТРЕЙДЕРОВ | обзор/отзывы
1998 год. FCA, НАУФОР. | +20% ПО КЕШБЭКУ | обзор/отзывы
2007 год. БОНУС $1500 НА СЧЕТ. |
STARTUP BONUS $1500 | обзор/отзывы
 2007 год. The FC. ФОРЕКС / ЦИФРОВЫЕ КОНТРАКТЫ ОТ 1$ | обзор / отзывы
2007 год. The FC. ФОРЕКС / ЦИФРОВЫЕ КОНТРАКТЫ ОТ 1$ | обзор / отзывы
Как и с чего начать торговлю с брокерской конторой?
В первую очередь, необходимо заключить договор, где разъяснены права и обязанности сторон
Стоит обратить внимание на то, сколько составляет процент комиссионных, каково качество программного обеспечения, количество предоставляемых услуг и отзывы.Обязательно убедитесь, что у брокера есть необходимый вам терминал.Далее трейдер создает личный аккаунт, где в зависимости от платформы потребуются ввести личные данные. После появляется опция открытия торгового счета
Далее клиент самостоятельно выбирает торговую платформу и пополняет счет.Заключительный этап – проведение сделок. Здесь и начинается реальная работа на бирже, в ходе которой можно будет наглядно увидеть, как работает фондовый рынок.
Зачем нужен брокер и как его выбрать?
Возведение комплексных чисел в степень
Начнем со всеми любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применении известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:. Аналогичную формулу можно вывести для квадрата разности, а также для куба суммы и куба разности. Но эти формулы более актуальны для задач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.
Что делать, если комплексное число нужно возвести, скажем, в 5-ю, 10-ю или 100-ю степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень справедлива формула:
Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел , нужно перемножить их модули и сложить аргументы:
Аналогично для показательной формы: если , то:
Просто до безобразия.
Пример 10
Дано комплексное число , найти .
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра: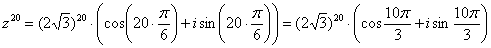
Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе . Для удобства делаем дробь правильной: , после чего становится хорошо видно, что можно убавить один оборот: . Надеюсь всем понятно, что и – это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Любители стандартов везде и во всём могут переписать ответ в виде: (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя – ни в коем случае не ошибка.
Пример 11
Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа , ,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить: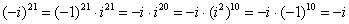
Пример 13
Возвести в степень комплексные числа ,
Это пример для самостоятельного решения.
Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
С алгебраической формой комплексного числа мы уже познакомились, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.
Сложение комплексных чисел
Пример 1
Сложить два комплексных числа ,
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел и , если ,
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
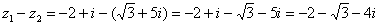
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .
Рассчитаем вторую разность:
Здесь действительная часть тоже составная:
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел ,
Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
Надеюсь, всем было понятно, что
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4
Даны комплексные числа , . Найти частное .
Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть
Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).
Распишу подробно:
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:
Редко, но встречается такое задание:
Пример 5
Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).
Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :
Пример 6
Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что
Определение комплексного числа. Операции над комплексными числами.
Определение. Комплексными числами называются выражения вида , в которых и — некоторые действительные числа, а — символ, называемый мнимой единицей.
Множество комплексных чисел обычно обозначается (от слова complex).
Введём понятие равенства и операции сложения и умножения для комплексных чисел.
- Два комплексных числа и равны тогда и только тогда, когда и .
-
Суммой комплексных чисел и называется число
(1)
-
Произведением комплексных чисел и называется число
(2)
Обычно комплексное число обозначают одной буквой, чаще всего (пишут ). При этом число называется действительной частью числа и обозначается (от слова real); пишут или . Число называется мнимой частью числа и обозначается (от слова imagine); пишут .
Множество комплексных чисел содержит в себе множество действительных чисел: любое действительное число можно представить в виде . Числа вида называются чисто мнимыми и обозначаются .
Пользуясь формулой (2), найдём
То есть
(3)
Заметим, что формулу (2) запоминать не нужно, так как она легко получается, если в произведении двучленов и заменить по формуле (3) на :
Пример 1. Найти сумму и произведение комплексных чисел и Решение. Пользуясь формулой (1), находим сумму:
Учитывая, что , находим произведение:
Свойства операций над комплексными числами
- Коммутативность сложения: для любых комплексных чисел и .
- Ассоциативность сложения: для любых комплексных чисел , и .
- для любого комплексного числа .
- Для любых комплексных чисел и существует комплексное число такое, что . Это число называется разностью комплексных чисел и и обозначается .
- Коммутативность умножения: для любых комплексных чисел и .
- Ассоциативность умножения: для любых комплексных чисел , и .
- Закон дистрибутивности: для любых комплексных чисел , и .
- для любого комплексного числа .
- Для любых двух комплексных чисел и , , существует число такое, что . Это число называется частным комплексных чисел и и обозначается .
Все эти свойства напрямую следуют из определения операций над комплексными числами. Докажем здесь свойство 9.
Пусть , , (неравенство числа нулю означает, что хотя бы одно из чисел и не равно нулю), . Тогда равенство записывается так: Приравнивая действительные и мнимые части, получаем, что числа и удовлетворяют системе уравнений:
Эта система уравнений имеет единственное решение
то есть
(4)
Эту формулу можно не запоминать. Далее мы покажем более простой способ нахождения частного двух комплексных чисел.
Определение. Пусть задано комплексное число . Число называется комплексно сопряжённым числу и обозначается .
Произведение комплексных чисел — всегда действительное число, большее нуля. Действительно, пусть , тогда
Определение. Модулем комплексного числа называется действительное число, равное .
Заметим, что .
Покажем теперь простой способ для нахождения частного двух комплексных чисел.
Здесь мы умножили числитель и знаменатель дроби на число, комплексно сопряжённое знаменателю. В результате в знаменателе получилось действительное число.
Пример 2. Найти разность и частное комплексных чисел
Решение. Находим разность:
Частное находим, домножая числитель и знаменатель дроби на число, комплексно сопряжённое знаменателю:
Формула Эйлера
Математики часто употребляют показательную форму. Числа комплексной плоскости записывают в виде выражения
z = r × ei×ϴ , которая вытекает из формулы Эйлера.

Такая запись получила широкое распространение для практического вычисления физических величин. Форма представления в виде показательных комплексных чисел особенно удобна для инженерных расчетов, где возникает необходимость рассчитать цепи с синусоидальными токами и необходимо знать значение интегралов функций с заданным периодом. Сами расчеты служат инструментом при конструировании различных машин и механизмов.
Примеры
Следуя приведенным правилам и формулам комплексных чисел, легко можно ими оперировать.
Рассмотрим простейшие примеры.
Задача 1. Используя равенство 3y +5 x i= 15 — 7i, определить x и y.
Решение. Вспомним определение комплексных равенств, тогда 3y = 15, 5x = -7. Следовательно, x = -7 / 5, y = 5.
Задача 2. Вычислить значения 2 + i28 и 1 + i135.
Решение. Очевидно, 28 — четное число, из следствия определения комплексного числа в степени имеем i28 = 1, значит, выражение 2 + i28 = 3. Второе значение, i135 = -1, тогда 1 + i135 = 0.
Задача 3. Вычислить произведение значений 2 + 5i и 4 + 3i.
Решение. Из общих свойств умножения комплексных чисел получаем (2 + 5i)Х( 4 + 3i) = 8 — 15 + i(6 + 20). Новое значение будет -7 + 26i.
Задача 4. Вычислить корни уравнения z3 = -i.
Решение. Вариантов, как найти комплексное число, может быть несколько. Рассмотрим один из возможных. По определению, ∣ — i∣ = 1, фаза для -i равна -р / 4. Исходное уравнение можем переписать в виде r3*ei3ϴ = e-p/4+pk, откуда z = e-p / 12 + pk/3, для любого целого k.
Множество решений имеет вид (e-ip/12, eip/4, ei2p/3).
Модуль и фаза
Для завершения описания комплексного множества предложим два важных определения.
Зная теорему Пифагора, легко вычислить длину луча в полярной системе координат.
r = ∣z∣ = √(x2 + y2), такая запись на комплексном пространстве носит название «модуль» и характеризует расстояние от 0 до точки на плоскости.
Угол наклона комплексного луча к вещественной прямой ϴ принято называть фазой.
Из определения видно, что реальная и мнимая части описываются с помощью циклических функций. А именно:
- x = r × cos(ϴ);
- y = r × sin(ϴ);
Обратно, фаза имеет связь с алгебраическими значениями через формулу:
ϴ = arctan(x / y) + µ, поправка µ вводится для учета периодичности геометрических функций.
Формула Эйлера
Математики часто употребляют показательную форму. Числа комплексной плоскости записывают в виде выражения
z = r × ei×ϴ , которая вытекает из формулы Эйлера.

Такая запись получила широкое распространение для практического вычисления физических величин. Форма представления в виде показательных комплексных чисел особенно удобна для инженерных расчетов, где возникает необходимость рассчитать цепи с синусоидальными токами и необходимо знать значение интегралов функций с заданным периодом. Сами расчеты служат инструментом при конструировании различных машин и механизмов.
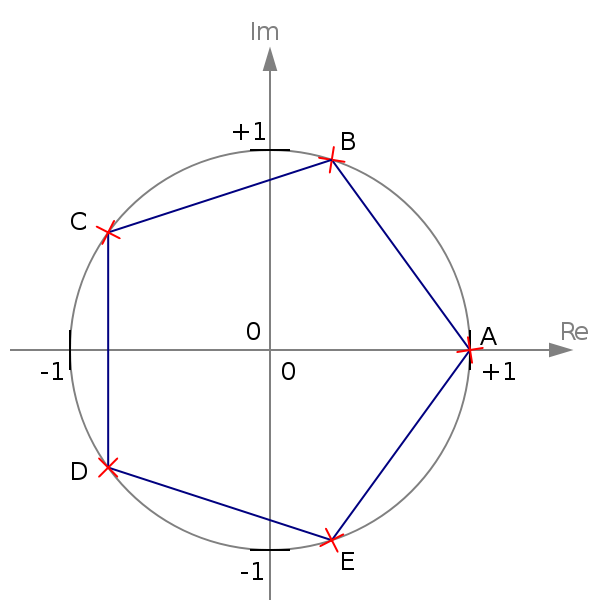
Тригонометрическая запись
Вспомним полярную систему координат и определение тригонометрических функций sin и cos. Очевидно, что с помощью этих функций можно описать расположение любой точки на плоскости. Для этого достаточно знать длину полярного луча и угол наклона к вещественной оси.
Определение. Запись вида ∣z ∣, умноженное на сумму тригонометрических функций cos(ϴ) и мнимой части i ×sin(ϴ), называется тригонометрическим комплексным числом. Здесь применяется обозначение угол наклона к вещественной оси
ϴ = arg(z), а r = ∣z∣, длина луча.
Из определения и свойств тригонометрических функций, следует очень важная формула Муавра:
zn = rn × (cos(n × ϴ) + i × sin(n × ϴ)).
Используя эту формулу, удобно решать многие системы уравнений, содержащие тригонометрические функции. Особенно когда возникает задача возведения в степень.