Дисперсия случайной величины

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E или first moment M.

Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:

где x_i – значение, которое может принимать случайная величина, а р(x_i) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:

где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).

Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Пример

Пусть случайная величина X{\displaystyle \displaystyle X} имеет стандартное непрерывное равномерное распределение на ,1{\displaystyle \displaystyle }, то есть её плотность вероятности задана равенством

fX(x)={1,x∈,1,x∉,1.{\displaystyle f_{X}(x)=\left\{{\begin{matrix}1,&x\in \\0,&x\not \in .\end{matrix}}\right.}

Тогда математическое ожидание квадрата случайной величины равно

MX2=∫1x2dx=x33|1=13{\displaystyle M\left=\int \limits _{0}^{1}\!x^{2}\,dx=\left.{\frac {x^{3}}{3}}\right\vert _{0}^{1}={\frac {1}{3}}},

и математическое ожидание случайной величины равно

MX=∫1xdx=x22|1=12{\displaystyle M\left=\int \limits _{0}^{1}\!x\,dx=\left.{\frac {x^{2}}{2}}\right\vert _{0}^{1}={\frac {1}{2}}}

Дисперсия случайной величины равна

DX=MX2−(MX)2=13−(12)2=112{\displaystyle D=M\left-(M)^{2}={\frac {1}{3}}-\left({\frac {1}{2}}\right)^{2}={\frac {1}{12}}}

Первые шаги на пути к открытию дисперсии

Как было сказано выше, световой поток при прохождении через призму разлагается на цветовой спектр, который Исаак Ньютон достаточно детально изучил в свое время. Результатом его исследований стало открытие явления дисперсии в 1672 году. Научный интерес к свойствам света появился еще до нашей эры. Знаменитый Аристотель уже тогда заметил, что солнечный свет может иметь разные оттенки. Ученый утверждал, что характер цвета зависит от «количества темноты», присутствующей в белом свете. Если ее много, то возникает фиолетовый цвет, а если мало, то красный. Великий мыслитель также говорил о том, что основным цветом световых лучей является белый.

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

Показатели описательной статистики
Среднее арифметическое
Стандартное отклонение
Коэффициент вариации
Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

Ширина интервала, куда попадает рост всех студентов, – 18 см.
В распределении рост наиболее близок к середине этого интервала.
Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
Дисперсия – это среднее значение отклонений возведенное в квадрат.
Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Свойства

Дисперсия любой случайной величины неотрицательна: DX⩾;{\displaystyle D\geqslant 0;}
Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;
Если случайная величина равна константе, то её дисперсия равна нулю: Da={\displaystyle D=0.} Верно и обратное: если DX=,{\displaystyle D=0,} то X=MX{\displaystyle X=M} почти всюду.
Дисперсия суммы двух случайных величин равна:

DX+Y=DX+DY+2cov(X,Y){\displaystyle D=D+D+2\,{\text{cov}}(X,Y)}, где cov(X,Y){\displaystyle {\text{cov}}(X,Y)} — их ковариация.
Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

D∑i=1nciXi=∑i=1nci2DXi+2∑1⩽i<j⩽ncicjcov(Xi,Xj){\displaystyle D\left=\sum _{i=1}^{n}c_{i}^{2}D+2\sum _{1\leqslant i<j\leqslant n}c_{i}c_{j}\,{\text{cov}}(X_{i},X_{j})}, где ci∈R{\displaystyle c_{i}\in \mathbb {R} }.
В частности, DX1+…+Xn=DX1+…+DXn{\displaystyle D=D+\ldots +D} для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю.
DaX=a2DX{\displaystyle D\left=a^{2}D}
D−X=DX{\displaystyle D\left=D}
DX+b=DX{\displaystyle D\left=D}
Если X=X(ω,τ){\displaystyle X=X(\omega ,\tau )} — случайная величина от пары элементарных событий (случайная величина на декартовом произведении вероятностных пространств), то

D(ω,τ)X=MωDτX+DωMτX{\displaystyle D_{(\omega ,\tau )}=M_{\omega }]+D_{\omega }]}

Замечания

Если случайная величина X{\displaystyle X} дискретная, то
D=∑i=1npi(xi−M)2,{\displaystyle D=\sum _{i=1}^{n}{p_{i}(x_{i}-M)^{2}},}
D=12∑i=1n∑j=1npipj(xi−xj)2=∑i=1n∑j=i+1npipj(xi−xj)2,{\displaystyle D={\frac {1}{2}}\sum _{i=1}^{n}\sum _{j=1}^{n}{p_{i}p_{j}(x_{i}-x_{j})^{2}}=\sum _{i=1}^{n}\sum _{j=i+1}^{n}{p_{i}p_{j}(x_{i}-x_{j})^{2}},}

где xi{\displaystyle x_{i}} — i{\displaystyle i}-ое значение случайной величины, pi=P(X=xi){\displaystyle p_{i}=P(X=x_{i})} — вероятность того, что случайная величина принимает значение xi{\displaystyle x_{i}}, n{\displaystyle n} — количество значений, которые принимает случайная величина.

Если случайная величина X{\displaystyle X} непрерывна, то:
D=∫−∞+∞(x−M)2f(x)dx{\displaystyle D=\int \limits _{-\infty }^{+\infty }{(x-M)^{2}f(x)dx}}

D=12∫−∞+∞∫−∞+∞(x2−x1)2f(x1)f(x2)dx1dx2{\displaystyle D={\frac {1}{2}}\int \limits _{-\infty }^{+\infty }\int \limits _{-\infty }^{+\infty }(x_{2}-x_{1})^{2}{f(x_{1})f(x_{2})dx_{1}dx_{2}}},

где f(x){\displaystyle f(x)} — плотность вероятности случайной величины.

В силу линейности математического ожидания справедлива формула:

DX=MX2−(MX)2{\displaystyle D=M-\left(M\right)^{2}}
Дисперсия является вторым центральным моментом случайной величины.
Дисперсия может быть бесконечной.
Дисперсия может быть вычислена с помощью производящей функции моментов U(t){\displaystyle U(t)}:

DX=MX2−(MX)2=U″()−(U′())2.{\displaystyle D=M-\left(M\right)^{2}=U»(0)-\left(U'(0)\right)^{2}.}
Дисперсия целочисленной случайной величины может быть вычислена с помощью .
Формула для вычисления смещённой оценки дисперсии случайной величины X{\displaystyle X} по последовательности реализаций этой случайной величины: X1…Xn{\displaystyle X_{1}…X_{n}} имеет вид:

S¯2=1n∑i=1n(Xi−X¯)2{\displaystyle {\overline {S}}^{2}={\frac {1}{n}}\sum \limits _{i=1}^{n}(X_{i}-{\overline {X}})^{2}}, где X¯=1n∑i=1nXi{\displaystyle {\overline {X}}={\frac {1}{n}}\sum \limits _{i=1}^{n}X_{i}} — выборочное среднее (несмещённая оценка MX{\displaystyle M}).

Для получения несмещённой оценки дисперсии случайной величины значение S¯2{\displaystyle {\overline {S}}^{2}} необходимо умножить на nn−1{\displaystyle {\frac {n}{n-1}}}. Несмещённая оценка имеет вид:

S~2=1n−1∑i=1n(Xi−X¯)2{\displaystyle {\widetilde {S}}^{2}={\frac {1}{n-1}}\sum \limits _{i=1}^{n}(X_{i}-{\bar {X}})^{2}}

Прогнозируем с Excel: как посчитать коэффициент вариации

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации.

Именно расчёту последнего стоит уделить особое внимание

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

Что такое коэффициент вариации и для чего он нужен?

Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации.

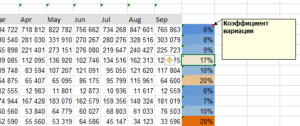
Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению.

Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.

Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим.

В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.

Как найти среднее квадратичное отклонение?

Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.

Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Вставьте формулу и укажите диапазон данных

Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

Откройте вкладку «».
Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Выберите «Процентный», а при необходимости укажите число десятичных знаков

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

Как работает стандартное отклонение в Excel

Добрый день!

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

=СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

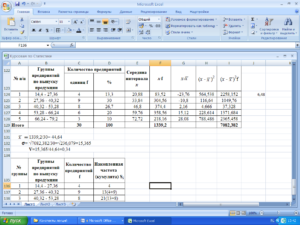
Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4). Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу: Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

=ЕСЛИ(H4

Условная дисперсия

Наряду с условным математическим ожиданием MX|Y{\displaystyle M} в теории случайных процессов используется условная дисперсия случайных величин DX|Y{\displaystyle D}.

Условной дисперсией случайной величины X{\displaystyle X} относительно случайной величины Y{\displaystyle Y} называется случайная величина

DX|Y=M(X−MX|Y)2|Y=MX2|Y−MX|Y2{\displaystyle D=M)^{2}|Y]=M-M^{2}}

Её свойства:

Условная дисперсия относительно случайной величины Y{\displaystyle Y} является Y-измеримой случайной величиной (то есть измерима относительно сигма-алгебры, порождённой случайной величиной Y{\displaystyle Y});
Условная дисперсия неотрицательна: DX|Y⩾{\displaystyle D\geqslant 0};
Условная дисперсия DX|Y{\displaystyle D} равна нулю тогда и только тогда, когда X=MX|Y{\displaystyle X=M} почти наверное, то есть тогда и только тогда, когда X{\displaystyle X} совпадает почти наверное с некоторой Y-измеримой величиной (а именно, с MX|Y{\displaystyle M});
Обычная дисперсия также может быть представлена как условная: DX=DX|1{\displaystyle D=D};
Если величины X{\displaystyle X} и Y{\displaystyle Y} независимы, случайная величина DX|Y{\displaystyle D} является константой, равной DX{\displaystyle D}.
Если X,Y{\displaystyle X,Y} — две числовые случайные величины, то

DX=MDX|Y+DMX|Y,{\displaystyle D=M]+D],}

откуда, в частности, следует, что дисперсия условного математического ожидания MX|Y{\displaystyle M} всегда меньше или равна дисперсии исходной случайной величины X{\displaystyle X}.

Свойства и проявления

Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и, следовательно, цвета). Обычно, чем меньше длина световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде:

у света красного цвета фазовая скорость распространения в среде максимальна, а степень преломления — минимальна,
у света фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна.

Однако в некоторых веществах (например, в парах иода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.

Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.

Белый свет разлагается в спектр и в результате прохождения через дифракционную решётку или отражения от неё (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.

По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу.

Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).

Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видеообъективов.

Огюстен Коши предложил эмпирическую формулу для аппроксимации зависимости показателя преломления среды от длины волны:

n=a+bλ2+cλ4{\displaystyle n=a+b/\lambda ^{2}+c/\lambda ^{4}},

где λ{\displaystyle \lambda } — длина волны в вакууме; a, b, c — постоянные, значения которых для каждого материала должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши. Впоследствии были предложены другие более точные, но и одновременно более сложные, формулы аппроксимации.