Высшая математика
Более высокие измерения и более общие классы чисел
| а | б | c | d | е | ж | грамм | час | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| а | б | c | d | е | ж | грамм | час |
Два белых слона ограничены полями противоположной четности; черный конь может прыгать только на клетки с переменной четностью.
Целочисленные координаты точек в евклидовых пространствах двух или более измерений также имеют четность, обычно определяемую как четность суммы координат. Например, гранецентрированная кубическая решетка и ее многомерные обобщения, решетки D n , состоят из всех целочисленных точек, сумма координат которых четна. Эта особенность проявляется в шахматах , где четность квадрата обозначается его цветом: слоны ограничены квадратами той же четности; кони чередуют ходы поочередно. Эта форма четности широко использовалась для решения проблемы изуродованной шахматной доски : если с шахматной доски убрать два противоположных угловых квадрата, то оставшаяся доска не может быть покрыта домино, потому что каждое домино покрывает по одной клетке каждой четности и есть еще два квадрата. одной четности, чем другой.
Четность порядковым номером , может быть определена , даже если число является предельное число, или предельное число плюс конечное число четное, и нечетным в противном случае.
Пусть R — коммутативное кольцо, а I — идеал в R с индексом 2. Элементы смежного класса можно назвать четными , а элементы смежного класса — нечетными . В качестве примера, пусть R = Z (2) быть локализации из Z в простом идеале (2). Тогда элемент R четный или нечетный , если и только если ее числитель так и в Z .
+я{\ displaystyle 0 + I}1+я{\ displaystyle 1 + I}
Теория чисел
Четные числа образуют идеал в кольце целых чисел, а нечетные — нет — это ясно из того факта, что единичный элемент для сложения, ноль, является элементом только четных чисел. Целое число является четным, если оно конгруэнтно 0 по модулю этого идеала, другими словами, если оно сравнимо с 0 по модулю 2, и нечетным, если оно сравнимо с 1 по модулю 2.
Все простые числа нечетны, за одним исключением: простое число 2. Все известные совершенные числа четны; неизвестно, существуют ли какие-либо нечетные совершенные числа.
Гипотеза Гольдбаха утверждает, что каждое четное целое число больше 2 может быть представлено как сумма двух простых чисел. Современные компьютерные вычисления показали, что эта гипотеза верна для целых чисел до 4 × 10 18 , но до сих пор не найдено общего доказательства .
Теория групп
Месть Рубика в решенном состоянии
Четность перестановки (как определено в абстрактной алгебре ) является четность числа транспозиций , в котором перестановка может быть разложенной. Например, (ABC) на (BCA) даже потому, что это можно сделать, поменяв местами A и B, затем C и A (две транспозиции). Можно показать, что никакая перестановка не может быть разложена как на четное, так и на нечетное количество транспозиций. Следовательно, приведенное выше определение является подходящим. В Кубике Рубика» , « Мегаминксе» и других поворотных головоломках ходы головоломки допускают только равные перестановки частей головоломки, поэтому четность важна для понимания конфигурационного пространства этих головоломок.
Теорема Фейта – Томпсона утверждает, что конечная группа всегда разрешима, если ее порядок — нечетное число. Это пример нечетных чисел, играющих роль в продвинутой математической теореме, где метод применения простой гипотезы «нечетного порядка» далеко не очевиден.
Анализ
Четность функции описывает , как его значения изменяются , когда ее аргументы заменяли их отрицания. Четная функция, такая как четная степень переменной, дает тот же результат для любого аргумента, что и для его отрицания. Нечетная функция, такая как нечетная степень переменной, дает для любого аргумента отрицание своего результата, если дано отрицание этого аргумента. Функция может быть ни нечетной, ни четной, а в случае f ( x ) = 0 может быть как нечетной, так и четной. Ряд Тейлора четной функции содержит только член которых показатель является четным числом, а ряд Тейлора нечетной функции содержит только член которых показатель является нечетным числом.
Комбинаторная теория игр
В комбинаторной теории игр , число зла этого число , которое имеет четное число 1 в его двоичном представлении , и одиозное число этого число , которое имеет нечетное число 1 в его двоичном представлении; эти числа играют важную роль в стратегии игры Kayles . Функция четности сопоставляет число с числом единиц в его двоичном представлении по модулю 2 , поэтому его значение равно нулю для злых чисел и единице для одиозных чисел. Последовательность Туэ-Морса , бесконечная последовательность нулей и единиц, имеет 0 в позиции i, когда i — зло, и 1 в этой позиции, когда i одиозно.
Чётные – нечётные числа

Что означают чётные и нечётные числа в духовной нумерологии. В изучении языка чисел это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Чётные числа
Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно духовной нумерологии? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У цифры 2 несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Возьмём для примера число 3 — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
———————————————————————————————
Обратите внимание!
С теплом, автор книги и этого сайта Иосиф Лазарев
———————————————————————————————
34667 | 8 комментариев
Математический контекст

Чётные (синие) — подмножество Z

Многоугольники с числами

Численные результаты теории обращаются к основной теореме арифметики и алгебраическим свойствам чётных чисел, поэтому вышеупомянутая конвенция имеет далеко идущие последствия. Например, факт, что положительные числа имеют уникальную факторизацию, означает, что для отдельного числа можно определить, имеет ли оно чётное или нечётное количество различных простых множителей. Поскольку 1 не является простым числом, а также не имеет простых множителей, оно является пустым произведением простых чисел; поскольку 0 — чётное число, 1 имеет чётное количество простых множителей. Из этого следует, что функция Мёбиуса принимает значение μ (1) = 1, что необходимо, чтобы она была мультипликативной функцией и работала формула вращения Мёбиуса.
Влияние четных и нечетных чисел на нашу жизнь
Со времен Пифагора было принято считать, что «женские» четные числа ассоциируются со злом потому, что легко расщепляются на две половины — и значит, можно говорить, что внутри них пустое пространство, первобытный хаос. А нечетное число расщепить на равные части без остатка не получится, следовательно, оно содержит внутри себя нечто цельное и даже священное (в Средние века некоторые философы-теологи утверждали, что внутри нечетных чисел живет Бог).
В современной нумерологии принято учитывать многие окружающие нас цифры — например, номера телефонов или квартир, даты рождения и знаменательных событий, числа имени и фамилии и т.п.
Наибольшее значение для нашей жизни имеет так называемое число судьбы, которое высчитывается по дате рождения. Нужно сложить все цифры этой даты и «свернуть» их до простого числа.
Скажем, вы родились 28 сентября 1968 года (28.09.1968). Складываем цифры: 2+8+0+9+1+9+ 6 -I- 8 = 43; 4 + 3 = 7. Следовательно, ваше число судьбы — 7 (как было сказано выше — число мистики и таинственности).
Точно так же можно проанализировать даты важных для вас событий. В этом отношении очень показательна судьба знаменитого Наполеона. Он родился 15 августа 1769 года (15.08.1769), следовательно, его число судьбы равно единице:
1 + 5 + 0 + 8 + 1 + 7 + 6 + 9 = 37; 3 + 7 = 10; 1 + 0 = 1.
Это нечетное число, согласно современной нумерологии, несет в себе активность, целеустремленность, инициативу -качества, благодаря которым Наполеон проявил себя. Он стал французским императором 2 декабря 1804 года (02.12.1804), число этой даты — девятка (0 + 2+1 + 2 + 1 + 8 + 0 + 4 = 18; 1 + 8 = 9), которая является числом высоких достижений. Он скончался 5 мая 1821 года (05.05.1821), число этого дня — четверка (0 + 5 + 0 + 5 + 1+ 8 + 2 + 1 = 22; 2 + 2 = 4), которая означает безвестность и поражение.
Древние люди не зря говорили, что цифры правят миром. Пользуясь знаниями нумерологии, вы легко можете подсчитать, какие события сулит та или иная дата — и в каких случаях следует воздержаться от ненужных действий.
Дополнительные приложения
В теории информации , бит четности добавляется в виде двоичного числа обеспечивает простую форму обнаружения ошибок кода . Если единственный бит в результирующем значении будет изменен, тогда он больше не будет иметь правильную четность: изменение бита в исходном номере дает ему четность, отличную от записанной, и изменение бита четности без изменения числа, которое он был полученный из снова дает неверный результат. Таким образом, все однобитовые ошибки передачи могут быть надежно обнаружены. Некоторые более сложные коды обнаружения ошибок также основаны на использовании нескольких битов четности для подмножеств битов исходного кодированного значения.
В духовых инструментах с цилиндрическим отверстием, фактически закрытых с одного конца, таких как кларнет у мундштука, генерируемые гармоники кратны основной частоте . (С цилиндрическими трубками, открытыми с обоих концов, используемыми, например, в некоторых органных упорах, таких как , гармоники даже кратны одной и той же частоте для данной длины отверстия, но это имеет эффект удвоения основной частоты и всего кратные этой основной частоте.) См. гармонический ряд (музыка) .
В некоторых странах нумерация домов выбрана так, что дома на одной стороне улицы имеют четные номера, а дома на другой стороне — нечетные. Точно так же среди пронумерованных автомагистралей в Соединенных Штатах четные числа в первую очередь указывают на автомагистрали с востока на запад, а нечетные числа — на автомагистрали север-юг. Среди номеров рейсов авиакомпаний четные числа обычно обозначают рейсы на восток или на север, а нечетные числа — на рейсы на запад или на юг.
Примечания
- , p. 34 Lemma B.2.2, The integer 0 is even and is not odd . Penner uses the mathematical symbol ∃, the existential quantifier, to state the proof: «To see that 0 is even, we must prove that ∃k (0 = 2 k ) and this follows from the equality 0 = 2 ⋅ 0.»
- Compare , p. 535 Fig. 1
- , pp. 535—536 «… numbers answer the question How many ? for the set of objects … zero is the number property of the empty set … If the elements of each set are marked off in groups of two … then the number of that set is an even number.»
- , pp. 535—536 «Zero groups of two stars are circled. No stars are left. Therefore, zero is an even number.»
- , p. 191
- , p. 537; compare her Fig. 3. «If the even numbers are identified in some special way … there is no reason at all to omit zero from the pattern.»
- , pp. 537—538 «At a more advanced level … numbers expressed as (2 × ▢) + 0 are even numbers … zero fits nicely into this pattern.»
- , pp. 30–33
- , pp. 376–377
- , p. 41
- , pp. 83–95
- See data throughout , and summary by , p. 837.
Четные и нечетные числа от 1 до 20 для дошкольников
Прежде чем выполнять задания, ребенок должен понять, что такое четные и нечетные числа от 1 до 20. Для этого можете распечатать и показать ему самое первое правило, которое он должен запомнить (можно прикрепить его к стене на время обучения). Объясните ребенку, что все числа, заканчивающиеся на 0, 2, 4, 6 и 8 — четные. Руководствуясь этим правилом, пусть ребенок ответит, на какие цифры должны заканчиваться нечетные числа (т.е. на 1, 3, 5, 7, 9).

Затем объясните ребенку, что все четные числа делятся на 2, а нечетные — не делятся на 2. Распечатайте второе правило:

Распечатайте Лист задания №1 и предложите ребенку обвести все четные числа, затем все нечетные числа.
Лист задание №1

Соедини числа по правилу — четное, нечетное
После того, как ребенок разобрался с понятием четных и нечетных чисел, предложите ему выполнить наши веселые задания в картинках. В первом задании обаятельного волка из всеми известного мультика «Ну погоди!» нужно привести к зайцу . Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами. Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами. Но соединять эти числа между собой нужно определенным образом. Пусть ребенок возьмет цветной карандаш и, начиная с самой маленькой цифры, начнет проводить путь только через кружки с четными числами, и самое главное — по порядку счета! Второе задание выполняется аналогично — только теперь путь прокладывается через кружки с нечетными числами.
Скачать задание «Соедини четные и нечетные числа» вы можете внизу страницы.

Посчитай и найди четные или нечетные числа
Еще одна проверка знаний четных и нечетных чисел для детей представлена в следующем упражнении. В первом задании ребенок должен сказать, какие продукты зайчики поделили поровну между собой. Чтобы узнать это, ребенку необходимо посчитать количество продуктов в каждой группе и сказать, четное оно или нечетное. Если четное — продукты поделятся поровну, если нечетное — то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?
Скачать задания по нахождению четных и нечетных чисел вы можете во вложениях внизу страницы.

Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу.
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках.
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями.
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.
Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.
В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое.
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10.
В образовании
Результат опроса школьников 1-6 классов в Великобритании
Вопрос, является ли ноль чётным числом, поднимался в системе школьного образования Великобритании. Проводились многочисленные опросы мнения школьников по данному вопросу. Выяснилось, что ученики по-разному оценивают чётность нуля: некоторые считают его чётным, некоторые — нечётным, иные полагают, что он является особым числом — и тем и другим одновременно или ни тем ни другим. Причём ученики пятых классов дают правильный ответ чаще, чем ученики шестых классов.
Как показали исследования, даже преподаватели в школах и вузах недостаточно осведомлены о чётности нуля. Так, например, порядка 2/3 преподавателей Университета Южной Флориды ответили «нет» на вопрос «Является ли ноль чётным числом?».
Почему ноль является чётным
Чтобы доказать, что ноль является чётным, можно непосредственно использовать стандартное определение «чётного числа». Число называют чётным, если это число кратно 2. Например, причиной того, что число 10 является чётным, является то, что оно равно 5 × 2. В то же время, ноль также является целым кратным 2, то есть 0 × 2, следовательно ноль является чётным.
Кроме того, можно объяснить, почему ноль является чётным, не применяя формальных определений.
Простые объяснения
Слева изображены группы с 0, 2 и 4 белыми объектами по парам; справа с 1, 3 и 5 объектами, где объект без пары обозначен красным. Область с 0 объектами не содержит красных объектов.
Ноль — это число, а числа используются для счёта. Если существует множество объектов, то числа используют, чтобы описать, сколько их. Ноль — это мера в случае, когда нет ни одного объекта; в более формальном смысле, это количество объектов в пустом множестве. Используя понятие чётности, создадим группы по паре объектов. Если объекты множества можно разделить и маркировать по парам без остатка, тогда количество объектов чётное. Если существует объект, не вошедший в группы, тогда количество объектов является нечётным. Пустое множество содержит 0 пар объектов и не имеет никакого остатка от такой группировки, поэтому ноль является чётным.
Все эти доводы можно проиллюстрировать, нарисовав объекты по парам. Трудно изобразить нулевые пары или показать отсутствие нечётного остатка, поэтому удобным будет нарисовать другие группы и сравнить их с нулём. Например, в группе из пяти объектов существуют две пары. Кроме того, в ней есть объект, который не относится ни к одной паре — поэтому число 5 является нечётным. В группе из четырёх объектов нет объектов, которые остались, только две пары, поэтому 4 является чётным. В группе только с одним объектом нет пар и есть один остаток, поэтому 1 является нечётным. В группе с нулём объектов нет пар и нет остатка, поэтому 0 является чётным.
Числа можно изобразить с помощью точек на числовой оси. Если на ней нанести чётные и нечётные числа, их общая закономерность становится очевидной, особенно если добавить и отрицательные числа:
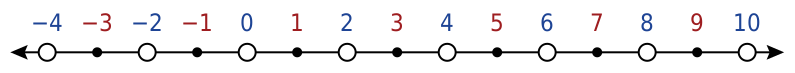
Чётные и нечётные числа чередуются между собой. Нет причины пропустить число ноль.
С помощью операции умножения чётность можно определить более формальным образом, используя арифметические выражения. Для каждого целого числа будет актуальна одна из форм: (2 × N) + 0 или (2 × N) + 1. Первое выражение соответствует чётным числам, а второе нечётным. Например, 1 является нечётным, поскольку 1 = (2 × 0) + 1, а 0 будет чётным, так как 0 = (2 × 0) + 0. Если такие выражения записать в таблицу по порядку, снова получим закономерность как на числовой оси.
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян».
В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
Чет и нечет
В нумерологии (науке о связях чисел с жизнью людей) нечетные числа (1, 3, 5, 7, 9, 11 и так далее) считаются выразителями мужского начала, которое в восточной философии называется — ян. Их также называют солнечными, потому что они несут энергию нашего светила. Такие цифры отражают поиск, стремление к чему-то новому.
Четные же числа (которые без остатка делятся на 2) говорят о женской природе (в восточной философии — инь) и энергетике Луны. Их суть в том, что они изначально тяготеют к двойке, поскольку делятся на нее. Эти цифры говорят о стремлении к логическим правилам отображения действительности и нежелании выйти за их пределы.
Другими словами: четные цифры более правильны, но в то же время более ограничены и прямолинейны. А нечетные способны помочь выбраться из скучного и серого бытия.
Нечетных чисел больше (ноль в нумерологии имеет собственное значение и не считается четным числом) — пять (1, 3, 5, 7, 9) против четырех (2,4,6, 8). Их более сильная энергия выражается в том, что при их сложении с четными числами снова получается нечетное число.
Противопоставление четных и нечетных чисел входит в общую систему противоположностей (один -много, мужчина — женщина, день -ночь, правый — левый, добро — зло и т.п.). При этом с нечетными числами связаны первые понятия, а с четными-вторые.
Таким образом, всякое нечетное число обладает мужскими характеристиками: властностью, резкостью, способностью к восприятию чего-то нового, а любое четное наделено женскими свойствами: пассивностью, стремлением сгладить любой конфликт.